Important Formulas: गणित में पैटर्न | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download
1. गणित में पैटर्न: गणित में संख्याओं, आकृतियों और दैनिक जीवन में पैटर्न पहचानना शामिल है। उदाहरण के लिए, सप्ताह के दिनों का एक चक्र में दोहराना।
2.गणित की वह शाखा जो पूर्ण संख्याओं में पैटर्न का अध्ययन करती है, उसे संख्यात्मक सिद्धांत कहा जाता है।
3. संख्या अनुक्रम: संख्याओं की क्रमबद्ध सूचियाँ जो एक विशेष नियम या पैटर्न का पालन करती हैं। उदाहरण के लिए: विषम संख्याओं के अनुक्रम में, प्रत्येक संख्या पिछले संख्या में 2 जोड़कर उत्पन्न होती है, 1 से शुरू होकर।
4.संख्या अनुक्रमों का दृश्यांकन पैटर्न को समझना आसान बना सकता है।
5. वर्ग संख्याएँ बिंदुओं के रूप में दिखाई जा सकती हैं जो एक सही वर्ग में व्यवस्थित होती हैं; 4 बिंदु 2x2 वर्ग बनाते हैं, और 9 बिंदु 3x3 वर्ग बनाते हैं।

6. त्रिकोणीय संख्याएँ बिंदुओं के रूप में प्रस्तुत की जा सकती हैं जो एक त्रिकोण बनाती हैं; उदाहरण के लिए, 1, 3, 6, 10, और 15 बिंदु 1, 2, 3, 4, और 5 पंक्तियों के साथ त्रिकोण बनाते हैं।
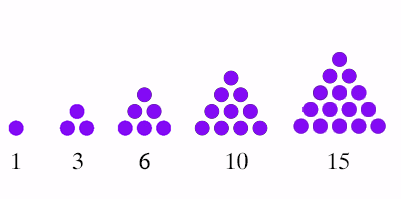
7.इन अनुक्रमों का दृश्यांकन यह समझने में मदद करता है कि संख्याएँ एक-दूसरे से कैसे संबंधित हैं, जैसे कि 36 एक वर्ग (6x6) और एक त्रिकोणीय संख्या दोनों है।
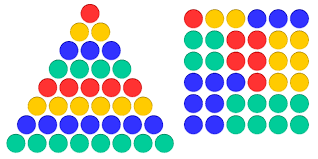
8.विभिन्न संख्या अनुक्रमों को दिलचस्प तरीकों से जोड़ा जा सकता है। उदाहरण के लिए, यदि आप लगातार विषम संख्याओं को जोड़ते हैं, जैसे 1, 1+3, 1+3+5, आदि, तो परिणाम हमेशा एक वर्ग संख्या बनाता है।
9.दृश्यांकन वर्ग संख्याओं से संबंधित योग को समझने और गणना करने में मदद करता है। उदाहरण के लिए, 1 बिंदु जोड़ने से 1x1 वर्ग बनता है, 3 बिंदु जोड़ने से 2x2 वर्ग बनता है, 5 और जोड़ने से 3x3 वर्ग बनता है, और इसी तरह।

10. गणित में, आकृतियों में भी पैटर्न पाए जा सकते हैं। ये पैटर्न ज्यामिति में खोजे जाते हैं और इनमें एक, दो, या तीन आयामों की आकृतियाँ शामिल हो सकती हैं।
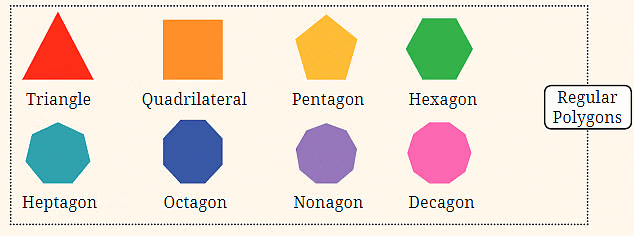
11. नियमित बहुभुज: यह अनुक्रम समान भुजाओं और कोणों वाले बहुभुजों से शुरू होता है। यह एक त्रिकोण (3 भुजाएँ) से शुरू होता है, फिर एक चतुर्भुज (4 भुजाएँ), उसके बाद एक पेंटागन (5 भुजाएँ) आता है, और इसी तरह आगे बढ़ता है। प्रत्येक चरण में आकृति में एक और भुजा जुड़ती है।
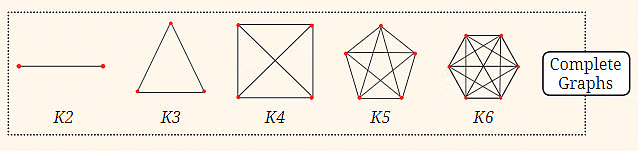
12. पूर्ण ग्राफ: यह अनुक्रम ग्राफों से संबंधित है जहाँ प्रत्येक बिंदु अन्य सभी बिंदुओं से जुड़ा होता है। यह दो बिंदुओं से शुरू होता है जो एक रेखा द्वारा जुड़े होते हैं, फिर तीन बिंदुओं से एक त्रिकोण बनता है, चार बिंदुओं से एक वर्ग बनता है जिसमें विकर्ण होते हैं, और यथासंभव जुड़ाव बढ़ता है।
13. स्टैक्ड स्क्वायर: यह अनुक्रम स्क्वायर को एक-दूसरे के ऊपर रखा गया दिखाता है, जो एकल स्क्वायर से शुरू होता है और छोटे स्क्वायरों से बने बड़े स्क्वायर में बढ़ता है।
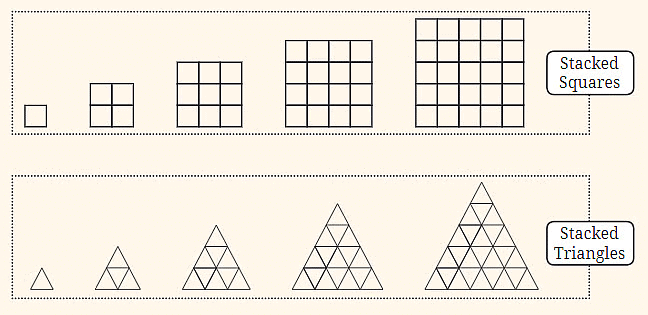
14. स्टैक्ड त्रिकोण: यह अनुक्रम त्रिकोणों को एक-दूसरे के ऊपर रखता है ताकि बड़े त्रिकोण बन सकें।
15. कोच स्नोफ्लेक: यह एक फ्रैक्टल आकृति है जो एक सरल त्रिकोण से शुरू होती है। प्रत्येक चरण में, छोटे त्रिकोण प्रत्येक भुजा पर जोड़े जाते हैं, जिससे एक अधिक जटिल पैटर्न बनता है जो बर्फ के फलक के समान होता है।

16. संबंध: स्टैक्ड स्क्वायर वर्ग संख्याओं से संबंधित हैं, जहाँ प्रत्येक चरण में स्क्वायर की एक और पंक्ति और कॉलम जोड़ा जाता है। पूर्ण ग्राफ कनेक्शनों की संख्या से संबंधित होते हैं, जो त्रिकोणीय संख्याओं के समान होते हैं। इन संबंधों को पहचानना ज्यामितीय और अंकगणितीय पैटर्न को समझने में मदद करता है।















