एनसीईआरटी समाधान: गणित में पैटर्न - Class 6 PDF Download

पृष्ठ 2

समस्या का समाधान करें

प्रश्न 1: क्या आप कुछ और उदाहरण सोच सकते हैं जहाँ गणित हमारे दैनिक जीवन में मदद करता है? उत्तर: यहाँ कुछ उदाहरण दिए गए हैं जहाँ गणित हमारे दैनिक जीवन में मदद करता है:

• पैसे का प्रबंधन (बजटिंग, खर्च)
• खाना बनाना (माप, अनुपात)
• खरीददारी (छूट, कुल राशि)
• घर में सुधार (मापन, क्षेत्रफल)
• यात्रा (दूरी, समय, खर्च)
• फिटनेस (कैलोरी, BMI)
• समय प्रबंधन (कार्यसूचियाँ)
• बागवानी (जगह, लेआउट)

ये उदाहरण दिखाते हैं कि गणित कैसे एक व्यावहारिक उपकरण है जो दैनिक समस्याओं को हल करने और सूचित निर्णय लेने में मदद करता है।

प्रश्न 2: गणित ने मानवता को आगे बढ़ाने में कैसे मदद की है? (आप कुछ उदाहरण सोच सकते हैं जैसे: वैज्ञानिक प्रयोग करना; हमारी अर्थव्यवस्था और लोकतंत्र को चलाना; पुल, घर या अन्य जटिल संरचनाएँ बनाना; टीवी, मोबाइल फोन, कंप्यूटर, साइकिल, ट्रेन, कार, विमान, कैलेंडर, घड़ियाँ आदि बनाना) उत्तर: गणित ने कई तरीकों से मानवता को आगे बढ़ाने में महत्वपूर्ण भूमिका निभाई है:

• विज्ञान (प्रयोग, प्राकृतिक कानून)
• अर्थव्यवस्था और लोकतंत्र (वित्तीय मॉडल, चुनाव विश्लेषण)
• अभियांत्रिकी (सुरक्षित भवन, पुल)
• प्रौद्योगिकी (कंप्यूटर, फोन, एल्गोरिदम)
• परिवहन (डिजाइन, गति, ईंधन, नेविगेशन)
• समय की माप (घड़ियाँ, कैलेंडर)
• चिकित्सा (खुराक, इमेजिंग, रोग मॉडलिंग)
• अंतरिक्ष (ग्रहों के पथ, अंतरिक्ष मिशन)

पृष्ठ 3

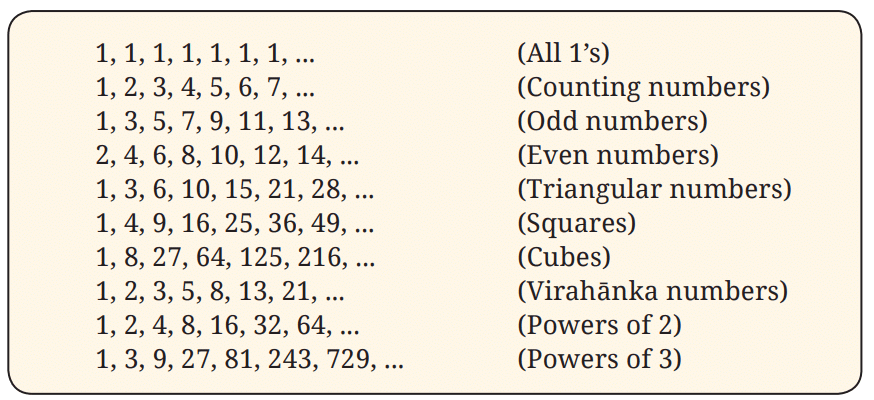
तालिका 1: संख्या अनुक्रमों के उदाहरण

समस्या का समाधान करें

प्रश्न 1: क्या आप तालिका 1 में प्रत्येक अनुक्रम में पैटर्न पहचान सकते हैं? उत्तर:

• (a) 1, 1, 1, 1, 1, 1, 1,…… संख्या ‘1’ दोहराई जा रही है।
• (b) 1, 2, 3, 4, 5, 6, 7,…… ‘1’ से शुरू होते हुए गिनती की संख्याएँ। 1 से शुरू करें। 1 जोड़ते रहें।
• (c) 1, 3, 5, 7, 9, 11, 13,….. ‘1’ से शुरू होते हुए विषम संख्याएँ। 1 से शुरू करें। 2 जोड़ते रहें।
• (d) 2, 4, 6, 8, 10, 12, 14,….. ‘2’ से शुरू होते हुए सम संख्याएँ। 2 से शुरू करें। 2 जोड़ते रहें।
• (e) 1, 3, 6, 10, 15, 21, 28,….. त्रिकोणीय संख्याएँ। 1 से शुरू करें। 2 जोड़ें: 1 + 2 = 3 फिर 3 जोड़ें: 3 + 3 = 6 फिर 4 जोड़ें: 6 + 4 = 10 और इसी तरह।
• (f) 1, 4, 9, 16, 25, 36, 49,….. गिनती की संख्याओं के वर्ग। 1st संख्या = 1 × 1 = 1, 2nd संख्या = 2 × 2 = 4, 3rd संख्या = 3 × 3 = 9, 4th संख्या = 4 × 4 = 16 और इसी तरह।
• (g) 1, 8, 27, 64, 125, 216,…… गिनती की संख्याओं के घन। 1st संख्या = 1 × 1 × 1 = 1, 2nd संख्या = 2 × 2 × 2 = 8, 3rd संख्या = 3 × 3 × 3 = 27, 4th संख्या = 4 × 4 × 4 = 64 और इसी तरह।
• (h) 1, 2, 3, 5, 8, 13, 21,…… विराहंक संख्याएँ (अंतिम 2 संख्याओं का योग)। 1st संख्या = 1, 2nd संख्या = 2, 3rd संख्या = 2nd संख्या + 1st संख्या = 2 + 1 = 3, 4th संख्या = 3rd संख्या + 2nd संख्या = 3 + 2 = 5, 5th संख्या = 4th संख्या + 3rd संख्या = 5 + 3 = 8, 6th संख्या = 5th संख्या + 4th संख्या = 8 + 5 = 13 और इसी तरह। 3rd संख्या से हर संख्या पिछले 2 संख्याओं का योग है।
• (i) 1, 2, 4, 8, 16, 32, 64,…… 2 की शक्तियाँ। 2⁰ = 1, 2¹ = 2, 2² = 2 × 2 = 4, 2³ = 2 × 2 × 2 = 8 और इसी तरह।
• (j) 1, 3, 9, 27, 81, 243, 729,…… 3 की शक्तियाँ। 3⁰ = 1, 3¹ = 3, 3² = 3 × 3 = 9, 3³ = 3 × 3 × 3 = 27 और इसी तरह।

Q2. अपने नोटबुक में तालिका 1 के प्रत्येक अनुक्रम को फिर से लिखें, साथ ही प्रत्येक अनुक्रम में अगली तीन संख्याएँ! प्रत्येक अनुक्रम के बाद, अपने शब्दों में लिखें कि अनुक्रम में संख्याएँ बनाने का नियम क्या है। उत्तर:

• (a) 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,……….. (1 को तीन बार दोहराएँ)
• (b) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…….. (अगली तीन गणना संख्याएँ)
• (c) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19,……….. (अगली तीन विषम संख्याएँ)
• (d) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20,……….. (अगली तीन सम संख्याएँ)
• (e) 1, 3, 6, 10, 15, 21, 28, 36, 45, 55,………. (अगली तीन त्रिकोणीय संख्याएँ)
• 28 + 8 = 36
• 36 + 9 = 45
• 45 + 10 = 55
• (f) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100,………. (अगली तीन वर्ग संख्याएँ)
• 8 × 8 = 64
• 9 × 9 = 81
• 10 × 10 = 100
• (g) 1, 8, 27, 64, 125, 216, 343, 512, 729,………. (अगली तीन घन संख्याएँ)
• 7 × 7 × 7 = 343
• 8 × 8 × 8 = 512
• 9 × 9 × 9 = 729
• (h) 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…………. (अगली विरहांक संख्याएँ)
• 13 + 21 = 34
• 21 + 34 = 55
• 34 + 55 = 89
• (i) 1, 2, 4, 8, 16, 32, 64, 128, 256, 512,……….. (पिछली संख्या को 2 से गुणा करें)
• 64 × 2 = 128
• 128 × 2 = 256
• 256 × 2 = 512
• (j) 1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683,………. (पिछली संख्या को 3 से गुणा करें)
• 729 × 3 = 2187
• 2187 × 3 = 6561
• 6561 × 3 = 19683

पृष्ठ 4 और 5

तालिका 2 कुछ संख्या अनुक्रमों का चित्रात्मक प्रतिनिधित्व

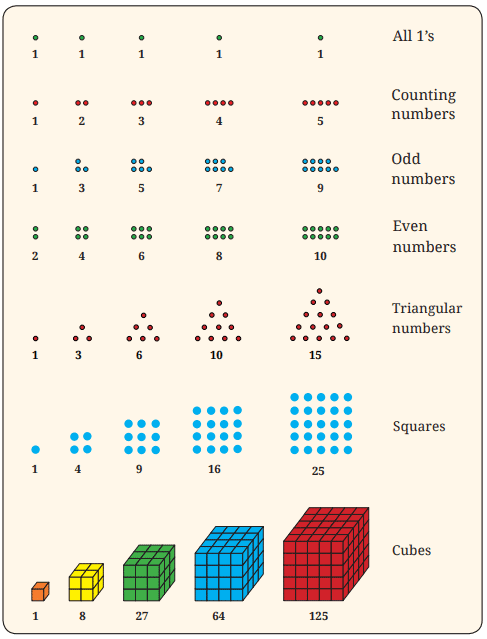
Q1. तालिका 2 में संख्या अनुक्रमों के चित्रात्मक प्रतिनिधित्व को अपने नोटबुक में कॉपी करें, और प्रत्येक अनुक्रम के लिए अगली चित्र बनाएँ! उत्तर:

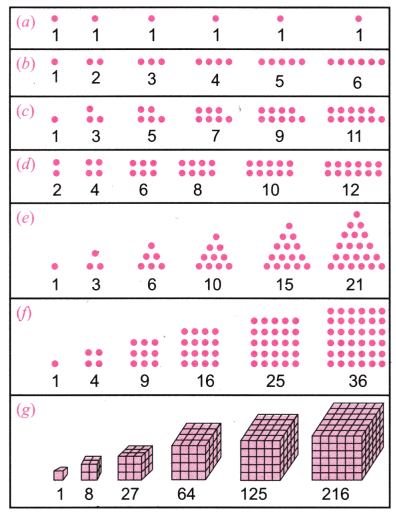
Q2. (a) 1, 3, 6, 10, 15,…… को त्रिकोणीय संख्याएँ क्यों कहा जाता है? (b) 1, 4, 9, 16, 25,…….. को वर्ग संख्याएँ या वर्ग क्यों कहा जाता है? (c) 1, 8, 27, 64, 125,…….. को घन क्यों कहा जाता है? उत्तर:

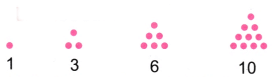
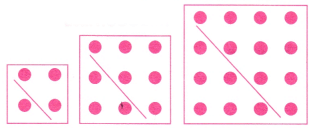
• (a) त्रिकोणीय संख्याएँ इसलिए कहा जाता है क्योंकि इन संख्याओं के बिंदुओं को त्रिकोण बनाने के लिए व्यवस्थित किया जा सकता है। 1, 3, 6, 10,…….. त्रिकोणीय संख्याएँ हैं। 1, 3, 6, 10,……… बिंदुओं को त्रिकोण बनाने के लिए व्यवस्थित किया जा सकता है। (नीचे चित्र देखें)
• (b) वर्ग संख्याएँ इसलिए कहलाती हैं क्योंकि इन संख्याओं के बिंदुओं को वर्ग बनाने के लिए व्यवस्थित किया जा सकता है। 1, 4, 9, 16,………. वर्ग संख्याएँ हैं। 1, 4, 9, 16,……… बिंदुओं को वर्ग बनाने के लिए व्यवस्थित किया जा सकता है। (नीचे चित्र देखें)

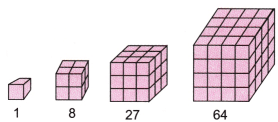
(c) घन (Cubes) को इसीलिए कहा जाता है क्योंकि इन कई एकक घनों (unit cubes) को मिलाकर एक घन बनाया जा सकता है। 1, 8, 27, 64,… ये घन संख्याएँ हैं। 1, 8, 27, 64,… एकक घनों को मिलाकर घन बनाए जा सकते हैं। (नीचे चित्र देखें)

Q3. आपने देखा होगा कि 36 एक त्रिकोणीय और वर्ग संख्या है! अर्थात, 36 बिंदुओं (dots) को त्रिकोण और वर्ग दोनों में सही तरीके से व्यवस्थित किया जा सकता है। अपने नोटबुक में इसका चित्र बनाएं! यह दर्शाता है कि एक ही संख्या को विभिन्न तरीकों से दर्शाया जा सकता है, और यह संदर्भ के अनुसार विभिन्न भूमिकाएँ निभा सकती है। कुछ अन्य संख्याओं को भी विभिन्न तरीकों से चित्रित करने का प्रयास करें! उत्तर: ऐसी तीन अन्य संख्याएँ हैं 1, 1225, और 41616। 1225 49वीं त्रिकोणीय संख्या है। इसके अलावा, 1225 को एक वर्ग द्वारा भी दर्शाया जा सकता है, जिसमें 36 बिंदु उसके किनारे पर हैं।

Q4. आप निम्नलिखित संख्याओं की श्रृंखला को क्या कहेंगे?

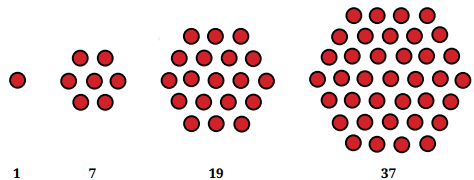
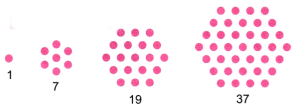
बिल्कुल सही, इन्हें षट्कोणीय संख्याएँ (hexagonal numbers) कहा जाता है! इन्हें अपने नोटबुक में बनाएं। श्रृंखला में अगली संख्या क्या है? उत्तर:

1वीं संख्या = 1
2वीं संख्या = 1 + 6 = 7 (2वीं संख्या = 1वीं संख्या + 6 × 1)
3वीं संख्या = 7 + 12 = 19 (3वीं संख्या = 2वीं संख्या + 6 × 2)
4वीं संख्या = 19 + 18 = 37 (4वीं संख्या = 3वीं संख्या + 6 × 3)
5वीं संख्या = 37 + 24 = 61 (5वीं संख्या = 4वीं संख्या + 6 × 4)
इस प्रकार, श्रृंखला में अगली संख्या 61 है।

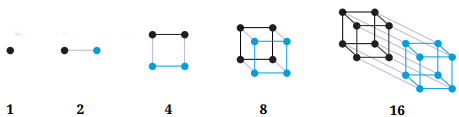
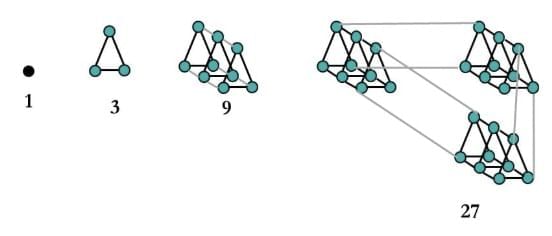
Q5. क्या आप 2 की शक्तियों (Powers of 2) की श्रृंखला को चित्रित करने के लिए चित्रात्मक तरीके सोच सकते हैं? 3 की शक्तियों (Powers of 3)? यहां 2 की शक्तियों के बारे में सोचने का एक संभावित तरीका है: उत्तर: 3 की शक्तियों के लिए चित्रात्मक प्रतिनिधित्व: 1, 3, 9, 27

उदाहरण: जब हम विषम संख्याओं को जोड़ना शुरू करते हैं तो क्या होता है?
1 = 1 = 1 का वर्ग
1 + 3 = 4 = 2 का वर्ग
1 + 3 + 5 = 9 = 3 का वर्ग
1 + 3 + 5 + 7 = 16 = 4 का वर्ग
1 + 3 + 5 + 7 + 9 = 25 = 5 का वर्ग
1 + 3 + 5 + 7 + 9 + 11 = 36 = 6 का वर्ग

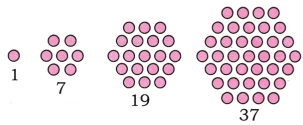
यह ऐसा क्यों होता है? क्या आपको लगता है कि यह हमेशा ऐसा ही होगा? उत्तर: यह इसलिए होता है क्योंकि प्रत्येक विषम संख्या को (2n – 1) के रूप में व्यक्त किया जा सकता है, जहाँ (n) एक सकारात्मक पूर्णांक है। जब हम पहले (n) विषम संख्याओं को जोड़ते हैं, तो हमें मिलता है: 1, 3, 5, … (2n – 1) = n। यह पैटर्न हमेशा के लिए जारी रहेगा क्योंकि यह संख्याओं की एक मूलभूत विशेषता है। विषम संख्याओं की श्रृंखला और उनके योग का पूर्ण वर्ग बनाना संख्या प्रणाली की एक अंतर्निहित विशेषता है।

हम एक वर्ग ग्रिड में बिंदुओं को विषम संख्याओं में कैसे विभाजित कर सकते हैं: 1, 3, 5, 7,…? उत्तर: हम बिंदुओं को एक वर्ग ग्रिड में विषम संख्याओं में विभाजित कर सकते हैं: 1, 3, 5, 7, इस प्रकार:

पृष्ठ 7

क्या आप समान चित्र बनाकर बता सकते हैं कि पहले 10 विषम संख्याओं का योग क्या है? उत्तर: पहले 10 विषम संख्याओं का योग = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = n² = (10)² = 10 × 10 = 100

अब, क्या आप एक समान चित्र की कल्पना करके या उसे आंशिक रूप से बनाकर बता सकते हैं कि पहले 100 विषम संख्याओं का योग क्या है? उत्तर: पहले 100 विषम संख्याओं का योग = 1 + 3 + 5 + … = n² = (100)² = 100 × 100 = 10,000

पृष्ठ 8 और 9

प्रश्न 1: क्या आप यह बता सकते हैं कि गिनती की संख्याओं को ऊपर और नीचे जोड़ने, अर्थात् 1, 1, 2, 1, 1, 2, 3, 2, 1,…, का योग वर्ग संख्याएँ क्यों देता है? उत्तर:

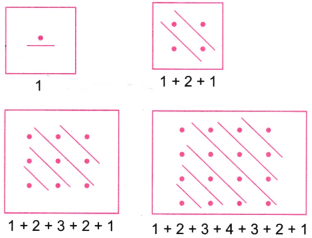
1 = 1 = (1)²
1 + 2 + 1 = 4 = (2)²
1 + 2 + 3 + 2 + 1 = 9 = (3)²
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 = (4)²
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25 = (5)²
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36 = (6)² और इसी तरह।

प्रश्न 2: क्या आप अपने चित्र का एक बड़ा संस्करण देखकर, या उसे आंशिक रूप से बनाकर देख सकते हैं कि 1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1 का मान क्या होगा? उत्तर: 1 + 2 + 3 + … + 100 + … + 3 + 2 + 1 = 100 × 100 = 10,000। इसलिए, यह 100² = 100 × 100 = 10,000 है।

प्रश्न 3: जब आप सभी 1 की श्रृंखला को जोड़ना शुरू करते हैं, तो आपको कौन सी श्रृंखला मिलती है? जब आप सभी 1 की श्रृंखला को ऊपर और नीचे जोड़ते हैं, तो आपको कौन सी श्रृंखला मिलती है?

उत्तर: ऊपर जोड़ना: 1 + 1 + 1 + 1 = 4
नीचे जोड़ना: 1 + 1 + 1 + 1 = 4
दोनों तरीकों से योग समान है।

प्रश्न 4: जब आप गिनती के नंबरों को जोड़ना शुरू करते हैं, तो आपको कौन सी श्रृंखला मिलती है? क्या आप एक छोटा चित्रात्मक स्पष्टीकरण दे सकते हैं?

उत्तर: गिनती के नंबरों को जोड़ना: 1, 1+2, 1+2+3, 1+2+3+4, या 1, 3, 6, 10

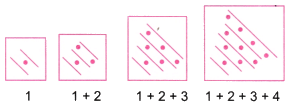
प्रश्न 5: जब आप लगातार त्रिकोणीय संख्याओं के जोड़े को जोड़ते हैं, तो क्या होता है? यानी, 1 और 3, 3 और 6, 6 और 10, 10 और 15 को लें,……..? आपको कौन सी श्रृंखला मिलती है? क्यों? क्या आप इसे एक चित्र के साथ समझा सकते हैं?

उत्तर: 1 + 3 = 4 = 2 × 2;
3 + 6 = 9 = 3 × 3;
6 + 10 = 16 = 4 × 4
उपरोक्त जोड़े वर्ग संख्याएँ देते हैं।

प्रश्न 6: जब आप 1 से शुरू करते हुए 2 की शक्तियों को जोड़ना शुरू करते हैं, यानी 1, 1+2, 1+2+4, 1+2+4+8,…..? अब इन संख्याओं में 1 जोड़ें — आपको कौन सी संख्याएँ मिलती हैं? यह क्यों होता है?

उत्तर: चलिए 1 से शुरू करके 2 की शक्तियों को जोड़ते हैं:
1 = 1
1 + 2 = 3
1 + 2 + 4 = 7
1 + 2 + 4 + 8 = 15
1 + 2 + 4 + 8 + 16 = 31
इस प्रकार श्रृंखला 1, 3, 7, 15, 31,… बनती है।
अब हम ऊपर की प्रत्येक संख्या में 1 जोड़ते हैं:
1 + 1 = 2 = 2¹
1 + 2 + 1 = 4 = 2 × 2 = 2²
1 + 2 + 4 + 1 = 8 = 2 × 2 × 2 = 2³
1 + 2 + 4 + 8 + 1 = 16 = 2 × 2 × 2 × 2 = 2⁴।
यह इसलिए होता है क्योंकि हम (1 + 1 = 2) जोड़ रहे हैं, इससे 2 की शक्ति बढ़ती है।

प्रश्न 7: जब आप त्रिकोणीय संख्याओं को 6 से गुणा करते हैं और 1 जोड़ते हैं, तो क्या होता है? आपको कौन सी श्रृंखला मिलती है? क्या आप इसे एक चित्र के साथ समझा सकते हैं?

उत्तर: त्रिकोणीय संख्याएँ हैं: 1, 3, 6, 10, 15, 21,…
1 × 6 + 1 = 7
3 × 6 + 1 = 19 (12 का बढ़ना, यानी 6 × 2)
6 × 6 + 1 = 37 (18 का बढ़ना, यानी 6 × 3)
10 × 6 + 1 = 61 (24 का बढ़ना, यानी 6 × 4)
15 × 6 + 1 = 91 (30 का बढ़ना, यानी 6 × 5)
हमें श्रृंखला मिलती है: 7, 19, 37, 61, 91,…

प्रश्न 8: जब आप षट्कोणीय संख्याओं को जोड़ना शुरू करते हैं, अर्थात् 1, 7, 19, 37,……? तो आपको कौन सी अनुक्रम मिलता है? क्या आप इसे एक घन की तस्वीर का उपयोग करके समझा सकते हैं?

उत्तर: षट्कोणीय संख्याएँ हैं: 1, 7, 19, 37,………. आइए इन्हें जोड़ते हैं:

• 1 = 1³ (1 का तीसरा घात)
• 1 + 7 = 8 = 2 × 2 × 2 = 2³ (2 का तीसरा घात)
• 1 + 7 + 19 = 27 = 3 × 3 × 3 = 3³ (3 का तीसरा घात)
• 1 + 7 + 19 + 37 = 64 = 4 × 4 × 4 = 4³ (4 का तीसरा घात)
• 1 + 7 + 19 + 37 + 61 = 125 = 5 × 5 × 5 = 5³ (5 का तीसरा घात)

प्रश्न 9: क्या आप तालिका 1 में अनुक्रमों में अपने खुद के पैटर्न या संबंध ढूँढ सकते हैं? क्या आप समझा सकते हैं कि ये क्यों होते हैं, किसी चित्र या अन्य तरीके से?

उत्तर: 3, 6, 9, 12, 15, 18,……… (3 के लगातार गुणांक)। 10, 15, 20, 25,…….. (पहली संख्या 10 है। फिर प्रत्येक पद में 5 की वृद्धि)

​पृष्ठ 10 और 11

तालिका 3: आकार अनुक्रमों के उदाहरण

प्रश्न 1: क्या आप तालिका 3 में प्रत्येक अनुक्रम में पैटर्न पहचान सकते हैं?

उत्तर:

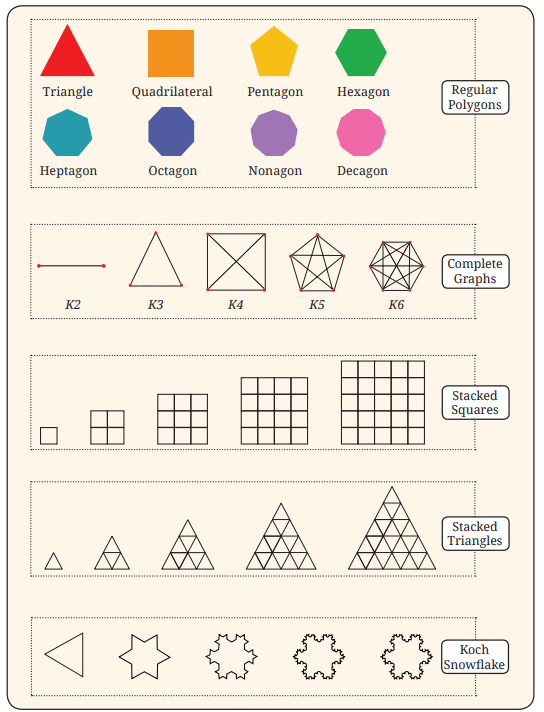
• (क) नियमित बहुपद: त्रिकोण, चतुर्भुज, पंचभुज, षट्भुज, (साइड की संख्या एक बार में 1 से बढ़ती है)। इसलिए, यह 3 से शुरू होने वाला एक निरंतर संख्या अनुक्रम है।
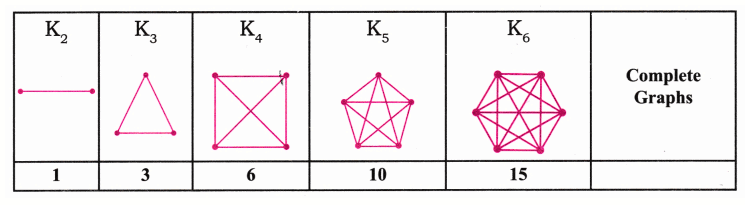
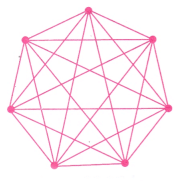
• (ख) पूर्ण ग्राफ़

यहाँ रेखाओं की संख्या इस प्रकार है:

• K2 = 1
• K3 = 3
• K4 = 6
• K5 = 10
• K6 = 15

इस प्रकार श्रृंखला बनती है 1, 3, 6, 10, 15,……. इसलिए यह एक त्रिकोणीय संख्या अनुक्रम है।

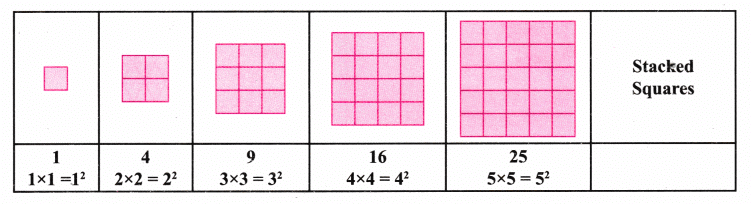
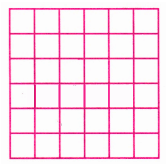
• (ग) स्टैक्ड स्क्वायर: प्रत्येक में छोटे वर्गों की संख्या:

श्रृंखला बनती है 1, 4, 9, 16, 25,……. इसलिए, यह वर्ग संख्याओं के अनुक्रम का प्रदर्शन है।

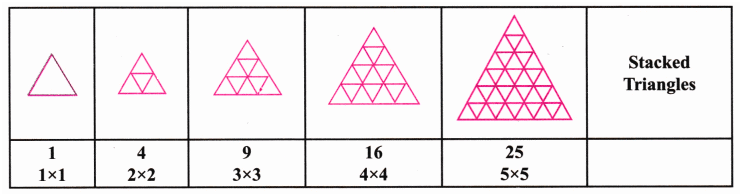
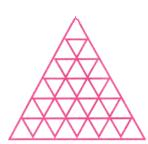
• (घ) स्टैक्ड त्रिकोण: प्रत्येक में छोटे त्रिकोणों की संख्या: इसलिए यह भी त्रिकोणों द्वारा प्रदर्शित एक वर्ग संख्या अनुक्रम है।
• (ङ) कोच स्नोफ्लेक: प्रत्येक में पक्षों की संख्या 4 गुना हो जाती है।

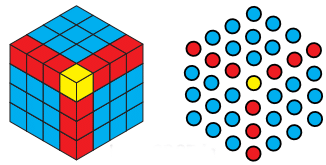
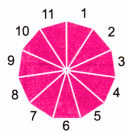
Q2. अपनी नोटबुक में तालिका 3 में प्रत्येक अनुक्रम को फिर से खींचने की कोशिश करें। क्या आप प्रत्येक अनुक्रम में अगला आकार बना सकते हैं? क्यों या क्यों नहीं? प्रत्येक अनुक्रम के बाद, अपने शब्दों में बताएं कि अनुक्रम में आकारों को बनाने का नियम या पैटर्न क्या है। उत्तर: (क) नियमित बहुभुज: 11 भुजाओं वाला बहुभुज। (हेंडेकागोन) (ख) K7 (ग) ढेर किए गए वर्ग

कुल वर्गों की संख्या = 6 × 6 = 36 (घ) ढेर किए गए त्रिकोणों की कुल संख्या = 1 + 3 + 5 + 7 + 9 + 11 = 36 (ङ) कोच स्नोफ्लेक। इसे समझें।

Q1. नियमित बहुभुजों के अनुक्रम में प्रत्येक आकार में भुजाओं की संख्या गिनें। आपको कौन सा संख्या अनुक्रम मिलता है? नियमित बहुभुजों के अनुक्रम में प्रत्येक आकार में कोनों की संख्या के बारे में क्या? क्या आपको वही संख्या अनुक्रम मिलता है? क्या आप समझा सकते हैं कि ऐसा क्यों होता है? उत्तर: दोनों अनुक्रम समान हैं क्योंकि नियमित बहुभुज में भुजाओं की संख्या और vertices की संख्या बराबर होती है।

Q2. पूर्ण ग्राफ़ों के अनुक्रम में प्रत्येक आकार में रेखाओं की संख्या गिनें। आपको कौन सा संख्या अनुक्रम मिलता है? क्या आप समझा सकते हैं कि ऐसा क्यों? उत्तर: इसलिए, हमें अनुक्रम मिलता है: 1, 3, 6, 10, 15,…… यह एक त्रिकोणीय संख्या अनुक्रम है।

Q3. ढेर किए गए वर्गों के अनुक्रम में प्रत्येक आकार में छोटे वर्गों की संख्या कितनी है? यह कौन सा संख्या अनुक्रम देता है? क्या आप समझा सकते हैं कि ऐसा क्यों? उत्तर:

हमें अनुक्रम मिलता है: 1, 4, 9, 16, 25, 36,………. इसलिए, हमें वर्ग संख्याओं का अनुक्रम मिलता है।

Q4. ढेर किए गए त्रिकोणों के अनुक्रम में प्रत्येक आकार में छोटे त्रिकोणों की संख्या कितनी है? यह कौन सा संख्या अनुक्रम देता है? क्या आप समझा सकते हैं कि ऐसा क्यों? (संकेत: अनुक्रम में प्रत्येक आकार में, प्रत्येक पंक्ति में कितने त्रिकोण हैं?) उत्तर: हमें अनुक्रम मिलता है: 1, 4, 9, 16, 25, 36, 49। यह वर्ग संख्याओं का अनुक्रम है। इसलिए, नीचे एक ढेर किया गया त्रिकोण जोड़ने से वर्ग अनुक्रम में अगली संख्या प्राप्त होगी।

प्रश्न 5: कोच स्नोफ्लेक क्रम में एक आकृति से दूसरी आकृति में जाने के लिए, प्रत्येक रेखा खंड ‘—’ को ‘स्पीड बंप’ __ⴷ__ से बदल दिया जाता है। जैसे-जैसे यह प्रक्रिया बार-बार की जाती है, परिवर्तन छोटे-छोटे रेखा खंडों के साथ और भी सूक्ष्म हो जाते हैं। कोच स्नोफ्लेक की प्रत्येक आकृति में कुल कितने रेखा खंड होते हैं? संबंधित संख्या अनुक्रम क्या है? (उत्तर 3, 12, 48, ..., अर्थात् 3 गुना 4 की शक्तियाँ; यह अनुक्रम तालिका 1 में नहीं दिखाया गया है।)

उत्तर: अनुक्रम 3, 12, 48, 192, 768, आदि 3 से शुरू होता है। प्रत्येक अगला पद पिछले पद को 4 से गुणा करके प्राप्त किया जाता है। इसी प्रकार, अगली कोच स्नोफ्लेक पुनरावृत्ति में, पिछले आकार की प्रत्येक रेखा के लिए चार नई रेखाएँ जोड़ी जाती हैं।