Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > Unit Test (Solutions) गणित में पैटर्न्स

Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

समय: 1 घंटा अधिकतम अंक: 30

सभी प्रश्नों का प्रयास करें।

प्रश्न संख्या 1 से 5 में प्रत्येक के 1 अंक हैं। प्रश्न संख्या 6 से 8 में प्रत्येक के 2 अंक हैं। प्रश्न संख्या 9 से 11 में प्रत्येक के 3 अंक हैं। प्रश्न संख्या 12 और 13 में प्रत्येक के 5 अंक हैं।

प्रश्न 1: अनुक्रम में अगला संख्या क्या है: 1, 4, 9, 16, 25? (1 अंक) उत्तर: 36 अनुक्रम में प्रत्येक संख्या अपनी स्थिति का वर्ग है (1², 2², 3² आदि), इसलिए अगला संख्या 6² = 36 है।

प्रश्न 2: पहले 10 त्रिकोणीय संख्याओं का योग ज्ञात करें। (1 अंक) उत्तर: 220 त्रिकोणीय संख्याएँ n(n + 1)/2 सूत्र द्वारा बनती हैं। पहले 10 का योग 1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 + 45 + 55 = 220 है।

प्रश्न 3: यदि आप पहले 6 विषम संख्याओं को जोड़ते हैं, तो आपको कौन सी वर्ग संख्या मिलती है? (1 अंक) उत्तर: 36 पहले 6 विषम संख्याओं (1, 3, 5, 7, 9, 11) का योग 36 है, जो एक वर्ग संख्या है (6²)।

प्रश्न 4: अगले तीन पदों के लिए पैटर्न जारी रखें: 1, 2, 4, 8, ___ , ___ , ___. (1 अंक) उत्तर: 16, 32, 64 प्रत्येक पद पिछले पद का दुगना है, इस प्रकार जारी रखते हुए: 8 × 2 = 16, 16 × 2 = 32, 32 × 2 = 64।

प्रश्न 5: निम्नलिखित में से कौन सा शक्तियों की अनुक्रम नहीं है? (1 अंक)

(i) 1, 2, 4, 8, 16
(ii) 1, 3, 9, 27, 81
(iii) 1, 5, 25, 125, 625
(iv) 1, 3, 6, 10, 15

उत्तर: (iv) 1, 3, 6, 10, 15 यह अनुक्रम त्रिकोणीय संख्याओं का प्रतिनिधित्व करता है, जो शक्तियाँ नहीं हैं, जहां प्रत्येक पद बिंदुओं द्वारा बनाए गए त्रिकोणीय रूप का प्रतिनिधित्व करता है।

प्रश्न 6: वर्ग संख्या 64 का चित्रण करें। (2 अंक) उत्तर: 64 को 8 × 8 के रूप में लिखा जा सकता है। इसलिए, इसे बिंदुओं द्वारा इस प्रकार दर्शाया जा सकता है:

Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 7: घन संख्या 1000 का चित्रण करें। (2 अंक) उत्तर: 1000 को 10 × 10 × 10 के रूप में लिखा जा सकता है। इस प्रकार,

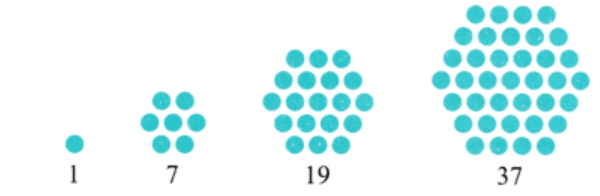
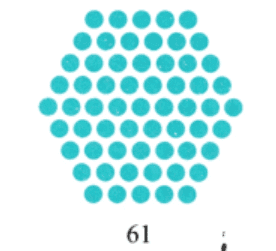
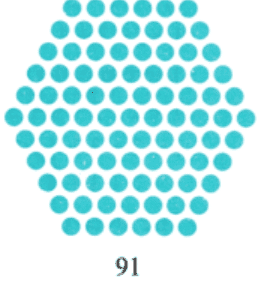
प्रश्न 8: हेक्सागोनल संख्या क्या है? इसे चित्रात्मक रूप में प्रस्तुत करें। (2 अंक) उत्तर: वे संख्याएँ जो एक हेक्सागोन के रूप में केन्द्र में एक बिंदु और चारों ओर हेक्सागोनल आकार में अन्य बिंदुओं के साथ दर्शाई जा सकती हैं। उदाहरण के लिए: 1, 7, 19, 37, 61, 91, …… चित्रात्मक प्रतिनिधित्व:

प्रश्न 9: निम्नलिखित संख्या अनुक्रमों को पूरा करें: (3 अंक)

(क) 1 3 5 ___ 9 11 = ____.
(ख) 1 ___ 3 4 3 2 1 = ____.
(ग) 1 2 3 __ 5 __ 7 ….. 11 __ …. 7 ___ 5 4 3 2 1 = 121

उत्तर:

(क) 1 3 5 7 9 11 = 36.
(ख) 1 2 3 4 3 2 1 = 16.
(ग) 1 2 3 4 5 6 7 8 9 10 11 10 9 8 7 6 5 4 3 2 1 = 121.

प्रश्न 10: पैटर्न की पहचान करें और दिए गए पैटर्न को पूरा करने के लिए अगले तीन नंबर लिखें। (3 अंक)

(क) 1, 3, 6, 10, 15, ….., …., ….
(ख) 1, 4, 9, 16, 25, …, …, ….
(ग) 1, 8, 27, 64, 125, …, …, ….

उत्तर:

(क) दिए गए पैटर्न के अनुसार: 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15; यह त्रिकोणीय संख्याओं का पैटर्न है। इसलिए, इस पैटर्न के अगले तीन नंबर हैं: 1 + 2 + 3 + 4 + 5 + 6 = 21, 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28, 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
(ख) दिए गए पैटर्न के अनुसार: 1 × 1 = 1, 2 × 2 = 4, 3 × 3 = 9, 4 × 4 = 16, 5 × 5 = 25; यह वर्ग संख्याओं का पैटर्न है। इसलिए, इस पैटर्न के अगले तीन नंबर हैं: 6 × 6 = 36, 7 × 7 = 49, 8 × 8 = 64.
(ग) दिए गए पैटर्न के अनुसार: 1 × 1 × 1 = 1, 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, 4 × 4 × 4 = 64, 5 × 5 × 5 = 125; यह घन संख्याओं का पैटर्न है। इसलिए, इस पैटर्न के अगले तीन नंबर हैं: 6 × 6 × 6 = 216, 7 × 7 × 7 = 343, 8 × 8 × 8 = 512.

प्रश्न 11: (i) अवधारणा: 15 एक त्रिकोणीय संख्या और एक वर्ग संख्या दोनों है। (3 अंक) कारण: यदि किसी संख्या की बिंदुओं की व्यवस्था को त्रिकोण और वर्ग दोनों रूप में दर्शाया जाए, तो उस संख्या को त्रिकोणीय और वर्ग संख्या या वर्ग-त्रिकोणीय संख्या कहा जाता है। दिए गए प्रश्न में, अवधारणा का एक कथन और कारण का एक कथन है। सही विकल्प चुनें:

(क) दोनों अवधारणा और कारण सत्य हैं और कारण अवधारणा का सही स्पष्टीकरण है।
(ख) दोनों अवधारणा और कारण सत्य हैं लेकिन कारण अवधारणा का सही स्पष्टीकरण नहीं है।
(ग) अवधारणा सत्य है और कारण गलत है।
(घ) अवधारणा गलत है और कारण सत्य है।

उत्तर: (घ) चूंकि, 15 बिंदुओं को त्रिकोण में व्यवस्थित किया जा सकता है, लेकिन वर्ग में नहीं। (ii) दिए गए अनुक्रम 1, 3, 6, 10, 15 के अगले दो अंशों का योग ज्ञात करें। उत्तर: 56 (21 28) त्रिकोणीय संख्याओं के अनुक्रम को जारी रखते हुए: 6(6 + 1)/2 = 21, 7(7 + 1)/2 = 28। योग है 21 + 28 = 49।

प्रश्न 12: पहले 7 केंद्रित षट्कोणीय संख्याओं का चित्रात्मक प्रदर्शन करें। (5 अंक) उत्तर: पहले छह केंद्रित षट्कोणीय संख्याएँ निम्नलिखित हैं: 1, 7, 19, 37, 61, 91, 127। चित्रात्मक प्रदर्शन:

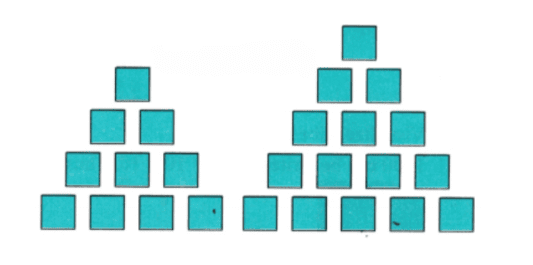
प्रश्न 13: केस आधारित प्रश्न (5 अंक) रिमा और दीवा वर्गीय काउंटरों के साथ खेल रही हैं। रिमा अपने काउंटर को निम्नलिखित प्रकार से व्यवस्थित करती है:

दीवा काउंटरों को निम्नलिखित प्रकार से व्यवस्थित करती है:

उनके एक दोस्त, रोहन, कहते हैं कि ये संख्या पैटर्न दिखा रहे हैं। उपरोक्त जानकारी के आधार पर, निम्नलिखित प्रश्नों का उत्तर दें।

(क) ये कौन से संख्या पैटर्न दिखा रहे हैं?
(ख) यदि रिमा का व्यवस्थित करना त्रिकोणीय संख्याओं का प्रतिनिधित्व कर रहा है, तो यदि वह उसी पैटर्न का पालन करती है, तो उसके अगले दो व्यवस्थाएँ क्या होंगी?
(ग) यदि दीवा उसी पैटर्न का अनुसरण करती है, तो उसके काउंटर का अगला आयोजन क्या होगा?

उत्तर: (क) रिमा के आयोजन द्वारा प्रदर्शित संख्या पैटर्न है: 1, 3, 6, …, जो त्रिकोणीय संख्याएँ हैं। दीवा का आयोजन पैटर्न को दर्शाता है: 1, 4, 9,…, जो वर्गीय संख्याएँ हैं। (ख) अगली त्रिकोणीय संख्याएँ 10 और 15 हैं। इसलिए, रिमा का आयोजन इन त्रिकोणीय संख्याओं के लिए निम्नलिखित है: (ग) अगली वर्गीय संख्या 16 है। इसलिए, दीवा का आयोजन संख्या 16 के लिए निम्नलिखित है:

The document Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: Unit Test (Solutions) गणित में पैटर्न्स for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for Unit Test (Solutions) गणित में पैटर्न्स have been prepared according to the Class 6 exam syllabus. Information about Unit Test (Solutions) गणित में पैटर्न्स covers topics like and Unit Test (Solutions) गणित में पैटर्न्स Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Unit Test (Solutions) गणित में पैटर्न्स.

Introduction of Unit Test (Solutions) गणित में पैटर्न्स in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & Unit Test (Solutions) गणित में पैटर्न्स in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about Unit Test (Solutions) गणित में पैटर्न्स

In this doc you can find the meaning of Unit Test (Solutions) गणित में पैटर्न्स defined & explained in the simplest way possible. Besides explaining types of Unit Test (Solutions) गणित में पैटर्न्स theory, EduRev gives you an ample number of questions to practice Unit Test (Solutions) गणित में पैटर्न्स tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

Extra Questions

pdf

Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

mock tests for examination

Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Semester Notes

Sample Paper

Important questions

Summary

Free

Viva Questions

past year papers

shortcuts and tricks

video lectures

Objective type Questions

Exam

ppt

Unit Test (Solutions) गणित में पैटर्न्स | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

practice quizzes

study material

Previous Year Questions with Solutions

MCQs

;

Additional Information about Unit Test (Solutions) गणित में पैटर्न्स for Class 6 Preparation

Unit Test (Solutions) गणित में पैटर्न्स Free PDF Download

The Unit Test (Solutions) गणित में पैटर्न्स is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Unit Test (Solutions) गणित में पैटर्न्स now and kickstart your journey towards success in the Class 6 exam.

Importance of Unit Test (Solutions) गणित में पैटर्न्स

The importance of Unit Test (Solutions) गणित में पैटर्न्स cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Unit Test (Solutions) गणित में पैटर्न्स Notes

Unit Test (Solutions) गणित में पैटर्न्स Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Unit Test (Solutions) गणित में पैटर्न्स. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Unit Test (Solutions) गणित में पैटर्न्स Notes on EduRev are your ultimate resource for success.

Unit Test (Solutions) गणित में पैटर्न्स Class 6 Questions

The "Unit Test (Solutions) गणित में पैटर्न्स Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Unit Test (Solutions) गणित में पैटर्न्स on the App

Students of Class 6 can study Unit Test (Solutions) गणित में पैटर्न्स alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Unit Test (Solutions) गणित में पैटर्न्स, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Unit Test (Solutions) गणित में पैटर्न्स is prepared as per the latest Class 6 syllabus.

Education Revolution