NCERT समाधान: रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

पृष्ठ 15

समस्या हल करें

प्रश्न 1:

क्या आप रिहान और शीतल को उनके उत्तर खोजने में मदद कर सकते हैं? उत्तर: हम एक बिंदु से गुजरने वाली अनंत रेखाएँ खींच सकते हैं, इसलिए रिहान इस बिंदु से अनंत बिंदु खींच सकता है।

दो बिंदुओं से हम केवल 1 रेखा खींच सकते हैं, शीतल केवल इन दोनों बिंदुओं से 1 रेखा खींच सकती है।

पृष्ठ 16

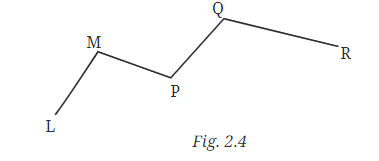
प्रश्न 2: चित्र 2.4 में रेखा खंडों के नाम बताएं। कौन से पांच चिह्नित बिंदु ठीक एक रेखा खंड पर हैं? कौन से दो रेखा खंडों पर हैं? उत्तर: रेखा खंड: LM, MP, PQ और QR। बिंदु L और R केवल एक रेखा खंड पर हैं। बिंदु M, P और Q दो रेखा खंडों पर हैं।

प्रश्न 3: चित्र 2.5 में दर्शाए गए किरणों के नाम बताएं। क्या T इन किरणों में से प्रत्येक का प्रारंभ बिंदु है?

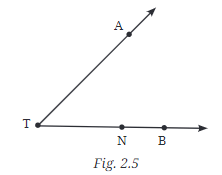
उत्तर: किरण और किरण (जिसे किरण TN भी कहा जा सकता है)। हाँ, T प्रत्येक 2 किरणों का प्रारंभ बिंदु है।

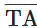
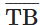
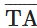
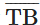
प्रश्न 4: एक मोटा चित्र बनाएं और निम्नलिखित को स्पष्ट करने के लिए उचित लेबल लिखें: (a) O पर मिलना। उत्तर:

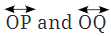
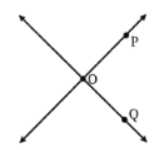
(b) बिंदु M पर इंटरसेक्ट करना। उत्तर:

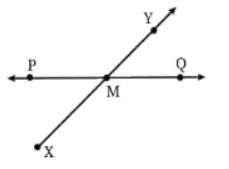
(c) रेखा I में बिंदु E और F हैं लेकिन बिंदु D नहीं है। उत्तर:

(d) बिंदु P AB पर है। उत्तर:

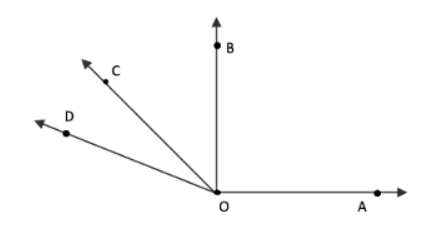
प्रश्न 5: चित्र 2.6 में नाम दें:

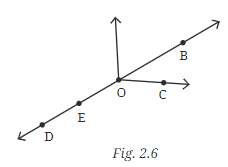
(a) पांच बिंदु। उत्तर: चित्र में पांच बिंदु D, E, O, C और B हैं।

(b) एक रेखा। उत्तर: चित्र में रेखा है।

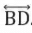
(c) चार किरणें। उत्तर: चित्र में चार किरणें हैं।

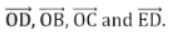
(d) पांच रेखा खंड। उत्तर: चित्र में पांच रेखा खंड हैं DE, EO, OC, BO और DO।

पृष्ठ 17

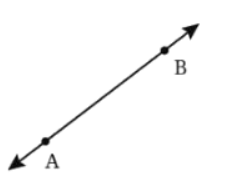
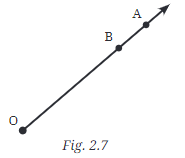
प्रश्न 6: यहाँ एक किरण है (चित्र 2.7)। यह O से शुरू होती है और बिंदु A के माध्यम से गुजरती है। यह बिंदु B के माध्यम से भी गुजरती है।

(a) क्या हम इसे नाम दे सकते हैं? क्यों? उत्तर: हाँ, किरण को नाम दिया जा सकता है क्योंकि किरण OA बिंदु B के माध्यम से भी जाती है। किरणों का नाम प्रारंभिक बिंदु से शुरू करते हुए और किरण पर किसी अन्य बिंदु के माध्यम से रखा जाता है। चूंकि किरण O से शुरू होती है और B और A दोनों के माध्यम से जाती है, इसे नामित किया जा सकता है।

(b) क्या हम इसे लिख सकते हैं? क्यों या क्यों नहीं? उत्तर: नहीं, हम इसे नहीं लिख सकते क्योंकि किरणें दिशात्मक होती हैं। किरण O से शुरू होती है और A के माध्यम से बढ़ती है, इसलिए यह O से A की दिशा को दर्शाती है। इसे इस तरह लिखना किरण A से शुरू होती है और O की ओर जाती है, जो इस संदर्भ में गलत है क्योंकि O प्रारंभिक बिंदु है।

पृष्ठ 18

विद्या ने अभी अपना पुस्तक खोला है। आइए हम विभिन्न परिस्थितियों में उसकी पुस्तक का आवरण खोलते हुए देखें।

प्रश्न: क्या आप इन सभी मामलों में कोण देख सकते हैं? क्या आप उनके भुजाओं और शीर्ष को चिह्नित कर सकते हैं? उत्तर: हाँ, मैं प्रत्येक मामले में कोण देख सकता हूँ। कोणों की भुजाएँ हरे रंग से चिह्नित की गई हैं और शीर्ष को प्रत्येक मामले में लाल बिंदु से चिह्नित किया गया है।

पृष्ठ 19 एवं 20

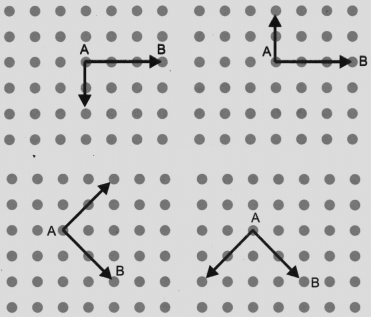
प्रश्न 1: क्या आप दिए गए चित्रों में कोण पा सकते हैं? कोण बनाने वाली किसी एक किरण को खींचें और कोण के शीर्ष का नाम दें।

∠BDC में, किरणें हैं और शीर्ष D है।

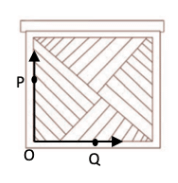
∠POQ में, किरणें हैं और शीर्ष O है।

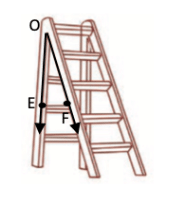
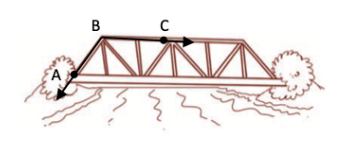
∠EOF में, किरणें हैं और शीर्ष O है।

∠ABC में, किरणें हैं और शीर्ष B है।

प्रश्न 2: ST और SR भुजाओं के साथ एक कोण खींचें और लेबल करें। उत्तर: ∠RST की भुजाएँ ST और SR हैं। चरण:

• सबसे पहले, एक बिंदु S बनाएं, जो शीर्ष होगा।
• फिर, S से शुरू होते हुए एक किरण खींचें और इसे एक दिशा में बढ़ाएं। दूसरे सिरे को T के रूप में लेबल करें (जिससे किरण ST बनती है)।
• फिर, S से शुरू होते हुए एक और किरण खींचें लेकिन एक अलग दिशा में। दूसरे सिरे को R के रूप में लेबल करें (जिससे किरण SR बनती है)।
• इससे ∠TSR एक कोण बनता है जिसमें S शीर्ष है, ST और SR भुजाएँ हैं।

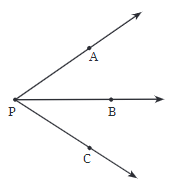
प्रश्न 3: समझाएँ कि ∠APC को ∠P के रूप में क्यों नहीं लेबल किया जा सकता है।

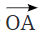
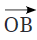
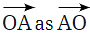
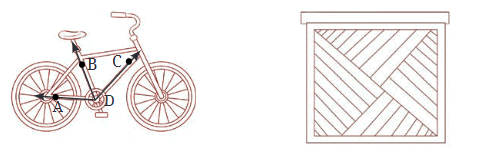
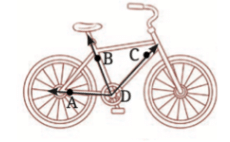
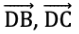
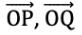
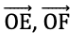
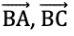
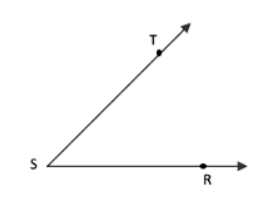
उत्तर: P पर तीन कोण हैं। ∠P का अर्थ ∠APB, ∠BPC या ∠APC हो सकता है। सही कोण प्राप्त करने के लिए इसे ∠APC, ∠APB या ∠BPC के रूप में नामित किया जाना चाहिए। यह भी ध्यान दें कि एकल बिंदु कोण नहीं बना सकता।

प्रश्न 4: दिए गए चित्र में चिह्नित कोणों के नाम बताएं।

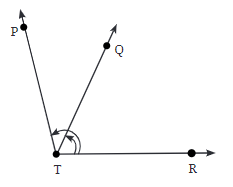
उत्तर: चित्र में चिह्नित कोण हैं:

• ∠RTQ
• ∠RTP

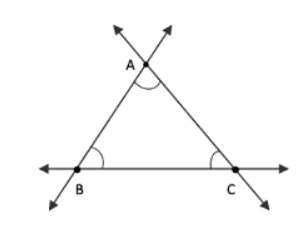
प्रश्न 5: अपने कागज पर कोई तीन बिंदु चिह्नित करें जो एक ही रेखा पर नहीं हैं। उन्हें A, B, C के रूप में लेबल करें। इन बिंदुओं के जोड़े के माध्यम से जाने वाली सभी संभावित रेखाएँ खींचें। आपको कितनी रेखाएँ मिलती हैं? उनके नाम बताएं। A, B, C का उपयोग करते हुए आप कितने कोण नामित कर सकते हैं? उन्हें लिखें और प्रत्येक को चित्र 2.9 की तरह एक वक्र के साथ चिह्नित करें।

उत्तर: इन बिंदुओं के जोड़ने से हमें तीन रेखाएँ मिलती हैं। इन बिंदुओं का उपयोग करते हुए तीन कोण बने हैं: ∠ABC, ∠ACB और ∠BAC।

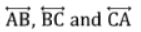
पृष्ठ 21

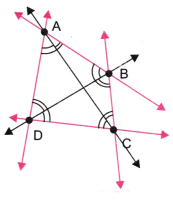
प्रश्न 6: अब अपने कागज पर कोई चार बिंदु चिह्नित करें ताकि उनमें से कोई तीन एक ही रेखा पर न हों। उन्हें A, B, C, D के रूप में लेबल करें। इन बिंदुओं के जोड़े के माध्यम से जाने वाली सभी संभावित रेखाएँ खींचें। आपको कितनी रेखाएँ मिलती हैं? उनके नाम बताएं। A, B, C, D का उपयोग करते हुए आप कितने कोण नामित कर सकते हैं? उन्हें सभी लिखें और प्रत्येक को चित्र 2.9 की तरह एक वक्र के साथ चिह्नित करें।

उत्तर: हमें छह रेखाएँ मिलती हैं। ये रेखाएँ हैं: AB, BC, CD, DA, AC और BD। इसके अलावा, हमें बारह कोण मिलते हैं। ये हैं: ∠BAC; ∠CAD, ∠BAD, ∠ABD, ∠DBC, ∠ABC, ∠BCA, ∠ACD, ∠BCD, ∠CDB, ∠CDA, ∠BDA।

प्रश्न: क्या हमेशा दो कोणों की तुलना करना आसान होता है?

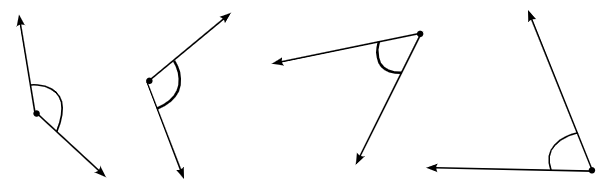
यहाँ कुछ कोण हैं। प्रत्येक कोण को लेबल करें। आप उनकी तुलना कैसे करेंगे? उत्तर: चित्र में कोणों की तुलना करने के लिए, मैं एक कोण को दूसरे पर रखूँगा या पारदर्शी कागज का उपयोग करके सीधे तुलना करूँगा कि कौन सा कोण बड़ा या छोटा है। यदि मैं प्रत्येक कोण की एक भुजा को दूसरी पर रखता हूँ, तो यह आसानी से देखा जा सकता है (दूसरी भुजा को देखकर) कि कौन सा छोटा या बड़ा है। इस विधि का उपयोग करके, मैं चित्र में कोणों की सटीक तुलना कर सकता हूँ।

पृष्ठ 23

प्रश्न: हम तुलना के लिए सुपरइम्पोज़िशन का उपयोग और कहाँ करते हैं? उत्तर: सुपरइम्पोज़िशन का उपयोग सामान्यतः वास्तविक जीवन की वस्तुओं जैसे कैंची, कंपास या अन्य उपकरणों में किया जाता है जो कोणों को शामिल करते हैं। हम इन वस्तुओं द्वारा बनाए गए कोणों को सुपरइम्पोज़ कर सकते हैं (जैसे, कैंची के ब्लेड के बीच का कोण) ताकि तुलना कर सकें कि कौन सा कोण बड़ा है या छोटा।

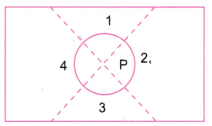
प्रश्न 1: एक आयताकार कागज की शीट को मोड़ें, फिर मोड़ के साथ एक रेखा खींचें। मोड़ और कागज के किनारों के बीच बने कोणों का नाम दें और उनकी तुलना करें। एक आयताकार कागज की शीट को मोड़कर विभिन्न कोण बनाएं और उन कोणों की तुलना करें। आपने कौन सा सबसे बड़ा और सबसे छोटा कोण बनाया?

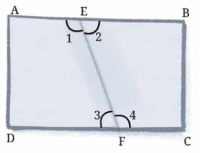
मोड़ के साथ बनाई गई रेखा के साथ बनाए गए कोण हैं ∠AEF, ∠BEF, ∠DFE और ∠CFE, जिन्हें 1, 2, 3 और 4 के साथ चिह्नित किया गया है। इनमें से ∠AEF और ∠CFE बड़े कोण हैं जबकि ∠BEF और ∠DFE छोटे कोण हैं।

प्रश्न 2: प्रत्येक मामले में, निर्धारित करें कि कौन सा कोण बड़ा है और क्यों। (क) ∠AOB या ∠XOY (ख) ∠AOB या ∠XOB (ग) ∠XOB या ∠XOC

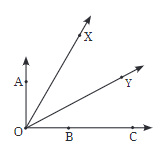
अपने दोस्तों के साथ चर्चा करें कि आपने कैसे तय किया कि कौन सा बड़ा है। उत्तर: (क) ∠AOB > ∠XOY, क्योंकि ∠XOY ∠AOB के भीतर है। इसका मतलब है कि ∠XOY ∠AOB का एक भाग है। (ख) ∠AOB > ∠XOB, क्योंकि ∠XOB ∠AOB के भीतर है। इसका मतलब है कि ∠XOB ∠AOB का एक भाग है। (ग) ∠XOB = ∠XOC, क्योंकि दोनों कोण समान किरणों से बनाए गए हैं।

प्रश्न 3: कौन सा कोण बड़ा है: ∠XOY या ∠AOB? कारण दें।

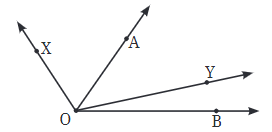
उत्तर: ∠XOB > ∠AOB, क्योंकि ∠AOB ∠XOB के भीतर है। इसका मतलब है कि ∠AOB ∠XOB का एक भाग है।

पृष्ठ 28

आइए एक सीधा कोण ∠AOB पर विचार करें। ध्यान दें कि कोई भी किरण इसे दो कोणों में विभाजित करती है, ∠AOC और ∠COB।

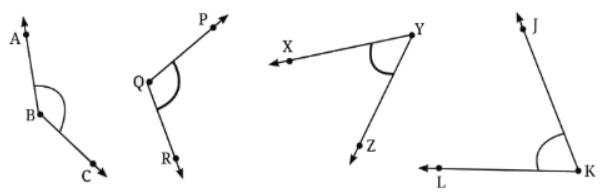
प्रश्न: क्या ऐसा चित्रित करना संभव है कि दोनों कोण एक-दूसरे के बराबर हों? उत्तर: यदि रेखा AB पर लंबवत हो जाए, तो दोनों कोण एक-दूसरे के बराबर हो जाएंगे।

प्रश्न: यदि एक सीधा कोण पूरे मोड़ के आधे द्वारा बनता है, तो सही कोण बनाने के लिए पूरे मोड़ का कितना हिस्सा होगा? उत्तर: यदि सीधा कोण पूरे मोड़ के आधे द्वारा बनता है, तो सही कोण एक-चौथाई (1/4) पूरे मोड़ द्वारा बनता है। निष्कर्ष के चरण:

• एक पूरा मोड़ 360 डिग्री है।
• एक सीधा कोण पूरे मोड़ का आधा है, इसलिए इसका माप 180 डिग्री है।
• एक सही कोण एक सीधे कोण का आधा है, इसलिए इसका माप 90 डिग्री है, जो पूरे 360 डिग्री के मोड़ का एक-चौथाई है।

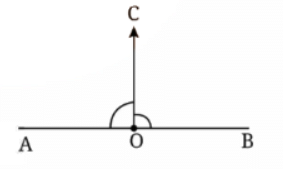
प्रश्न 1: आपकी कक्षा की खिड़कियों में कितने सही कोण हैं? क्या आपको अपनी कक्षा में अन्य सही कोण दिखाई देते हैं? उत्तर: एक खिड़की में 4 सही कोण होते हैं: ∠1, ∠2, ∠3 और ∠4। हाँ। दरवाजे के कोनों पर। कक्षा के काले बोर्ड के कोनों पर आदि।

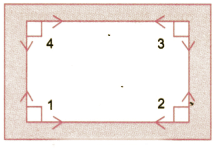
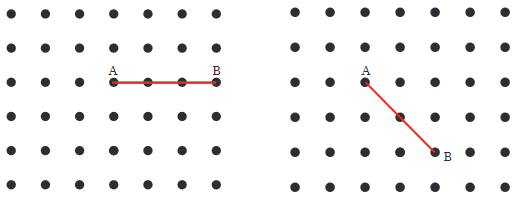
प्रश्न 2: चित्र में A को अन्य ग्रिड बिंदुओं से एक सीधी रेखा से जोड़ें ताकि एक सीधा कोण प्राप्त हो। इसे करने के सभी विभिन्न तरीके क्या हैं?

उत्तर: सीधा कोण बनाने के विभिन्न तरीके:

यह एक तरीके से किया जा सकता है।

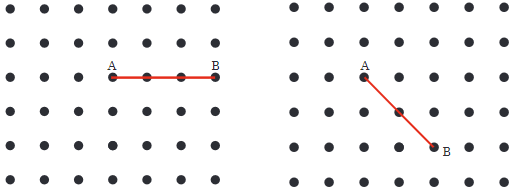
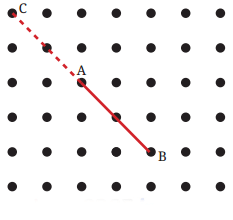
प्रश्न 3: अब चित्र में A को अन्य ग्रिड बिंदुओं से एक सीधी रेखा से जोड़ें ताकि एक सही कोण प्राप्त हो। इसे करने के सभी विभिन्न तरीके क्या हैं? संकेत: नीचे चित्र में दिखाए अनुसार रेखा को और बढ़ाएं। A पर सही कोण प्राप्त करने के लिए, हमें एक ऐसी रेखा खींचनी होगी जो सीधे कोण CAB को दो समान भागों में विभाजित करती है। उत्तर:

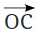
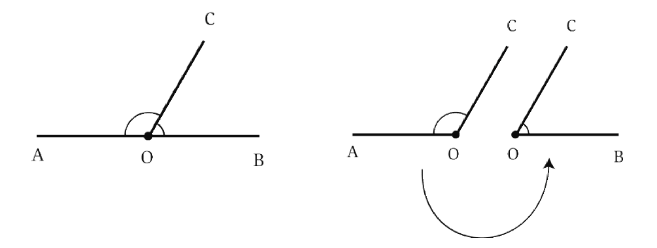
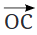
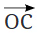
प्रश्न 4: कागज पर एक तिरछी क्रीज बनाएं। अब, एक और क्रीज बनाने की कोशिश करें जो तिरछी क्रीज के प्रति लंबवत हो। (क) अब आपके पास कितने समकोण हैं? बताएं कि ये कोण सही समकोण क्यों हैं। उत्तर: हमें चार समकोण मिलते हैं। मान लें कि P दोनों क्रीजों का इंटरसेक्शन बिंदु है। दोनों क्रीजें लंबवत रेखाएं हैं जो P पर मिलती हैं। इसलिए, सभी चार कोण समकोण हैं। (ख) विवरण दें कि आपने कागज को कैसे मोड़ा ताकि कोई और व्यक्ति जो इस प्रक्रिया को नहीं जानता, आपकी व्याख्या का पालन करके समकोण प्राप्त कर सके। उत्तर:

• चरण 1: एक शीट कागज लें और इसे मोड़ें।
• चरण 2: मोड़ पर क्रीज बनाएं।
• चरण 3: अब, फिर से कागज को मोड़ें ताकि क्रीज के दोनों भाग एक साथ आ जाएं।
• चरण 4: मोड़ पर क्रीज बनाएं।
• चरण 5: दोनों क्रीजों को खोलें। हमें दो लंबवत रेखाएं और चार समकोण प्राप्त होते हैं जैसा कि ऊपर दिखाया गया है।

समझें

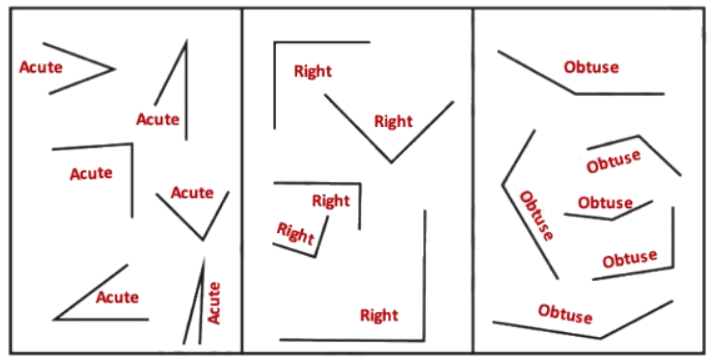
प्रश्न 1: पिछले चित्रों में तीव्र, समकोण, विस्तृत, और सीधी कोणों की पहचान करें। उत्तर:

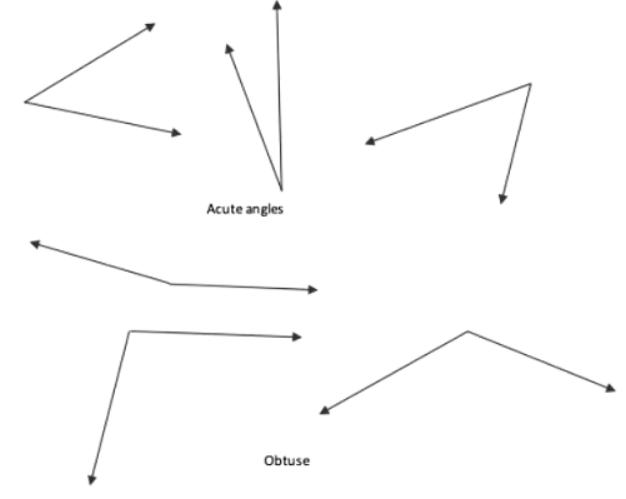
प्रश्न 2: कुछ तीव्र कोण और कुछ विस्तृत कोण बनाएं। उन्हें विभिन्न स्थितियों में चित्रित करें। उत्तर:

प्रश्न 3: क्या आप जानते हैं कि शब्द तीव्र और विस्तृत का क्या अर्थ है? तीव्र का अर्थ है तेज और विस्तृत का अर्थ है कुंद। आपको लगता है कि ये शब्द क्यों चुने गए हैं? उत्तर: शब्द ‘तीव्र’ का अर्थ है ‘तेज’। कोण का शीर्ष एक तेज नोक की तरह दिखाई देता है। शब्द ‘विस्तृत’ का अर्थ है ‘कुंद’। कोण का शीर्ष एक कुंद नोक की तरह दिखाई देता है।

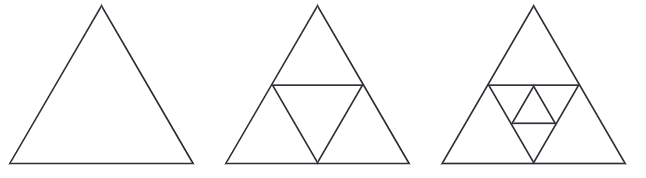
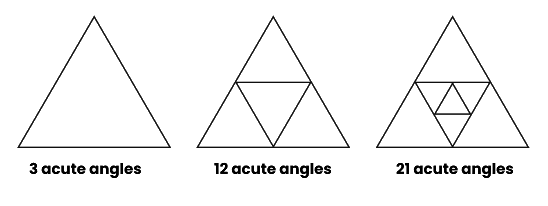
प्रश्न 4: नीचे दिए गए प्रत्येक चित्र में तीव्र कोणों की संख्या ज्ञात करें। अगला चित्र क्या होगा और उसमें कितने तीव्र कोण होंगे? क्या आप संख्याओं में कोई पैटर्न देख रहे हैं? उत्तर:

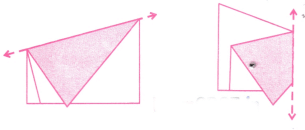
3 9=12 12 9 = 21 हर चरण में, कोणों की संख्या 9 से बढ़ती है। अगली आकृति इस प्रकार होगी: तेज कोणों की संख्या = 21 9 = 30

पृष्ठ 33

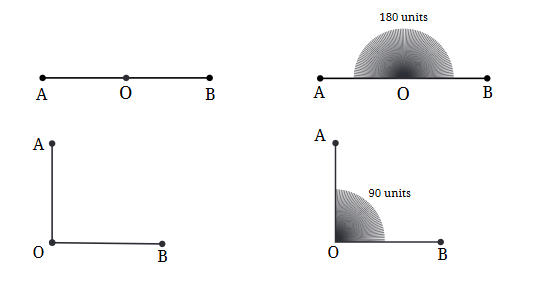
प्रश्न: एक सीधे कोण का माप डिग्री में क्या है? एक सीधा कोण एक पूर्ण घुमाव का आधा होता है। चूंकि एक पूर्ण घुमाव 360º है, एक आधा घुमाव 180º है। एक समकोण का माप डिग्री में क्या है? दो समकोण मिलकर एक सीधे कोण का निर्माण करते हैं। चूंकि एक सीधे कोण का माप 180º है, एक समकोण का माप 90º है।

उत्तर: एक सीधे कोण का माप 180º है और एक समकोण का माप 90º है।

पृष्ठ 34

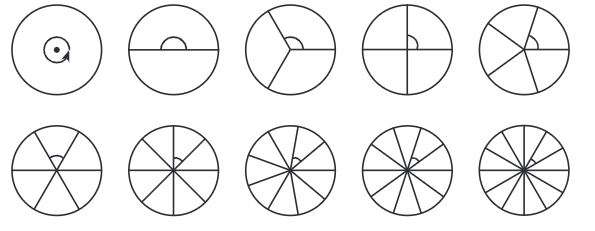
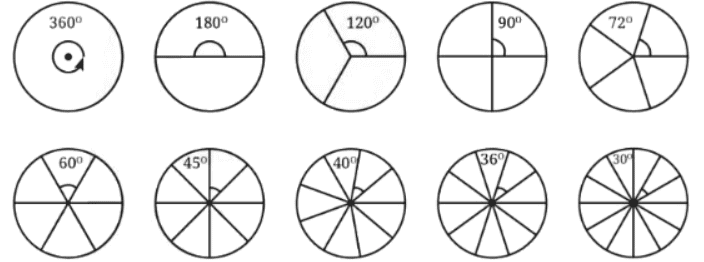
प्रश्न: वृत्त को 1, 2, 3, 4, 5, 6, 8, 9, 10 और 12 भागों में विभाजित किया गया है। परिणामी कोणों के डिग्री माप क्या हैं? निर्दिष्ट कोणों के पास डिग्री माप लिखें।

उत्तर:

पृष्ठ 35

समस्या को हल करें

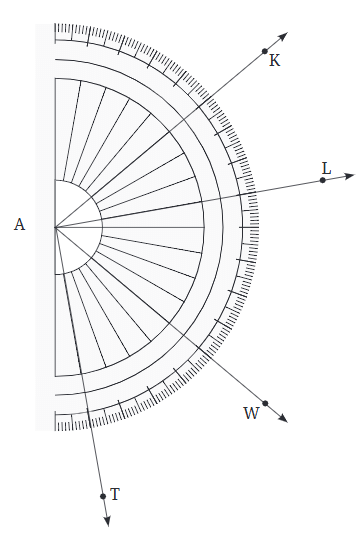
प्रश्न: निम्नलिखित कोणों के माप लिखें: (a) ∠KAL ध्यान दें कि इस कोण का शीर्षक प्रोट्रैक्टर के केंद्र के साथ मेल खाता है। इसलिए KA और AL के बीच 1 डिग्री कोण की इकाइयों की संख्या ∠KAL का माप देती है। गिनती करके, हमें ∠KAL = 30° मिलता है। क्या मध्यम आकार और बड़े आकार के चिह्नों का उपयोग करके, 5 या 10 में इकाइयों की संख्या गिनना संभव है? (b) ∠WAL (c) ∠TAK

उत्तर: (a) ∠KAL = 30º (b) ∠WAL = 50º (c) ∠TAK = 40º

पृष्ठ 36 और 37

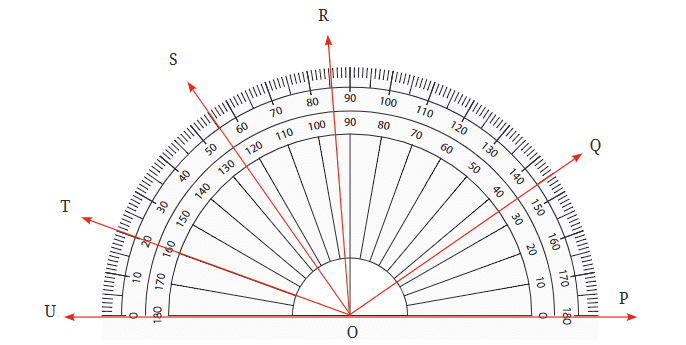
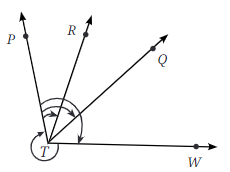
प्रश्न: आकृति में विभिन्न कोणों के नाम बताएं और उनके माप लिखें। क्या आपने ∠TOQ जैसे कोणों को शामिल किया? आपने कौन सा चिह्नण प्रणाली का उपयोग किया - आंतरिक या बाह्य? ∠TOS का माप क्या है?

उत्तर: हाँ, मैंने ∠TOQ जैसे कोणों को शामिल किया है। मैंने कोणों के अनुसार दोनों चिह्नण प्रणाली का उपयोग किया है - आंतरिक और बाह्य। ∠TOS का माप = 35º है।

पृष्ठ 40

सोचें

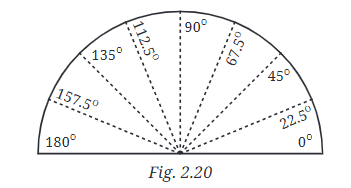
प्रश्न: चित्र में, हमारे पास ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = ____ क्यों? उत्तर: ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = 22.5º। सीधा कोण 8 समान भागों में विभाजित है, इसलिए, प्रत्येक कोण का माप 180º/8 = 22.5º है।

चित्र समझें

चित्र समझें

प्रश्न 1: अपने प्रोट्रैक्टर का उपयोग करके निम्नलिखित कोणों के डिग्री माप ज्ञात करें।

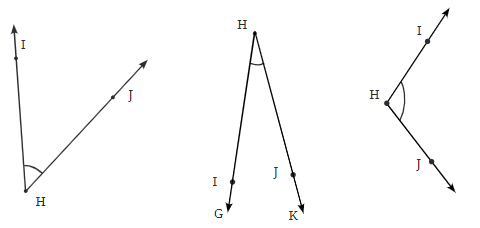
उत्तर: (a) ∠IHJ = 47° (b) ∠IHJ = 24° (c) ∠IHJ = 110°

प्रश्न 2: अपने कक्षा में विभिन्न कोणों के डिग्री माप ज्ञात करें। उत्तर: कालेबोर्ड का कोण = 90° डेस्क का कोण = 90°

पृष्ठ 41

प्रश्न 3: नीचे दिए गए कोणों के लिए डिग्री माप ज्ञात करें। क्या आपका पेपर प्रोट्रैक्टर यहाँ उपयोग किया जा सकता है! उत्तर: (a) ∠IHJ = 42° (b) ∠IHJ = 116° पेपर प्रोट्रैक्टर यहाँ उपयोग नहीं किया जा सकता।

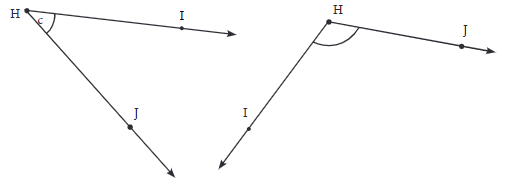
प्रश्न 4: नीचे दिए गए कोण का डिग्री माप जानने के लिए प्रोट्रैक्टर का उपयोग कैसे करें?

उत्तर: हमें रिफ्लेक्स ∠AOB का माप चाहिए। चरण 1: हम ∠AOB का माप ज्ञात करते हैं। चरण 2: हम 360° - ∠AOB ज्ञात करते हैं। यही आवश्यक माप है।

प्रश्न 5: निम्नलिखित कोणों के लिए माप ज्ञात करें और लिखें:

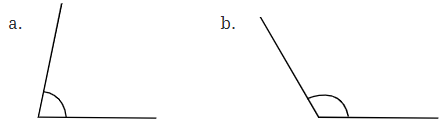
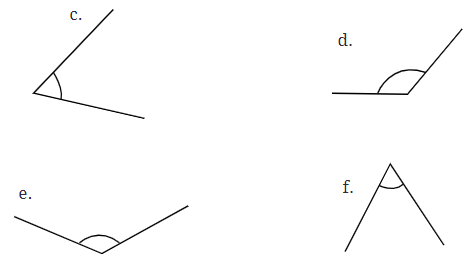
उत्तर: (a) दिए गए कोण का माप 80° है (b) दिए गए कोण का माप 120° है (c) दिए गए कोण का माप 60° है (d) दिए गए कोण का माप 130° है (e) दिए गए कोण का माप 130° है (f) दिए गए कोण का माप 60° है।

पृष्ठ 42

प्रश्न 6: ∠BXE, ∠CXE, ∠AXB, और ∠BXC के डिग्री माप ज्ञात करें।

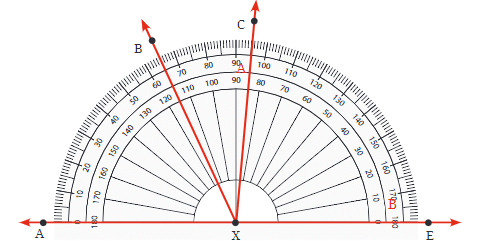
उत्तर: (a) ∠BXE = 115° (b) ∠CXE = 85° (c) ∠AXB = 65° (d) ∠BXC = 30°

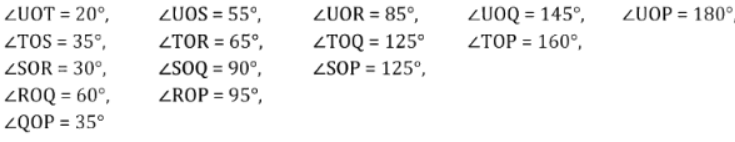
Q7: ∠PQR, ∠PQS, और ∠PQT के डिग्री माप ज्ञात करें।

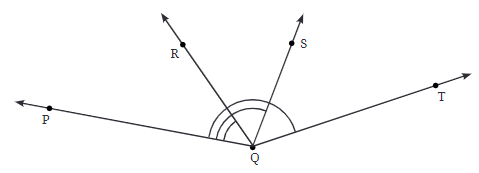
उत्तर: (क) ∠PQR = 45° (ख) ∠PQS = 105° (ग) ∠PQT = 150°

पृष्ठ 43

Q8: दिए गए निर्देशों के अनुसार पेपर क्राफ्ट बनाएं। फिर, कागज को पूरी तरह से खोलें और फोल्ड की गई रेखाओं पर मापें।

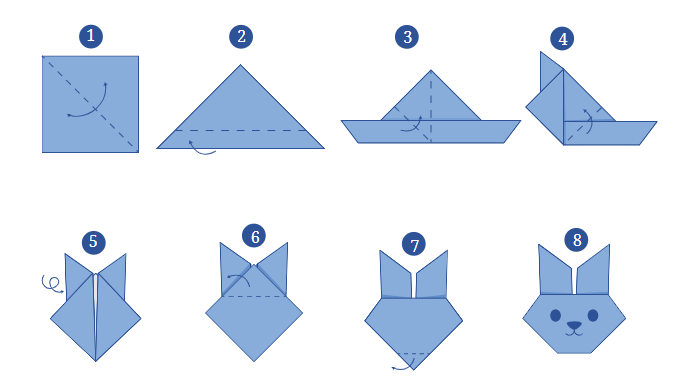
उत्तर:

• चरण 1: जब हम वर्गाकार कागज को तिरछा मोड़ते हैं, तो नीचे के कोनों पर दो समकोण (90º) बनते हैं और शीर्ष पर एक 45º कोण बनता है।
• चरण 2: मोड़ने के बाद, त्रिकोण का आधार समतल होता है, जिससे नीचे के कोनों पर 90º के कोण बनते हैं, जबकि शीर्ष शीर्ष 45º पर रहता है।
• चरण 3: जब हम आधार को ऊपर की ओर मोड़ते हैं, तो त्रिकोण के साथ मिलन स्थल पर एक छोटा समकोण (90º) बनता है।
• चरण 4: कान बनाने के लिए किनारों को मोड़ने से शीर्ष के पास तीव्र कोण बनते हैं, जो संभवतः लगभग 30º से 45º के बीच होते हैं।
• चरण 5: जैसे-जैसे हम किनारों को और अंदर मोड़ते हैं, त्रिकोणीय कानों में कोण और तेज हो सकते हैं, जिससे कानों के टिप्स पर लगभग 30º के करीब तीव्र कोण बनते हैं।
• चरण 6: ऊपर की ओर मोड़ने से खरगोश के चेहरे के टिप पर एक और तीव्र कोण बनता है, जो संभवतः लगभग 45º होता है।
• चरण 7: अंतिम मोड़ नीचे को तेज करता है, आधार पर 90º और कानों के पास 45º से 60º के बीच बनाए रखता है।
• चरण 8: पूर्ण खरगोश के चेहरे में, हमारे पास कई कोण होंगे: कान तीव्र कोण बनाते हैं (लगभग 30º से 45º)। चेहरे के किनारे के पास obtuse कोण बनता है, जो 120º के करीब होता है। चेहरे के किनारे 90º से 120º के बीच होते हैं, जो मोड़ों की सटीकता पर निर्भर करते हैं।

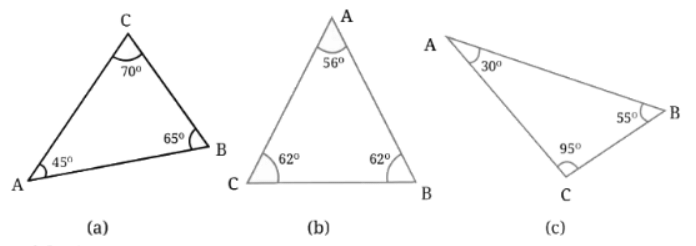
Q9: चित्र 2.21 (क) में दिखाए गए त्रिकोण के सभी तीन कोण मापें और संबंधित कोणों के पास माप लिखें। अब तीनों मापों को जोड़ें। आपको क्या मिलता है? चित्र 2.21 (ख) और (ग) में त्रिकोणों के लिए भी यही करें। अन्य त्रिकोणों के लिए भी प्रयास करें, और फिर सामान्यत: क्या होता है, इसके लिए एक अनुमान लगाएं!

उत्तर: (क) ∠ACB = 70º ; ∠CAB = 45º ; ∠ABC= 65º ΔABC के सभी कोणों का योग = ∠ACB + ∠CAB + ∠ABC = 70º + 45º + 65º = 180º (ख) ∠ACB = 62º ; ∠CAB = 55º ; ∠ABC= 63º ΔABC के सभी कोणों का योग = ∠ACB + ∠CAB + ∠ABC = 62º + 55º + 63º = 180º (ग) ∠ACB = 97º ; ∠CAB = 30º ; ∠ABC = 53º ΔABC के सभी कोणों का योग = ∠ACB + ∠CAB + ∠ABC = 97º + 30º + 53º = 180º हमने दिए गए गतिविधियों से यह अनुमान लगाया है कि किसी भी दिए गए त्रिकोण के सभी कोणों का योग हमेशा 180º होता है।

पृष्ठ 45

कोण कहाँ हैं? प्रश्न 1: घड़ी में कोण: (क) घड़ी की सुइयाँ अलग-अलग समय पर अलग-अलग कोण बनाती हैं। 1 बजे, सुइयों के बीच का कोण 30° है। ऐसा क्यों? (ख) 2 बजे का कोण क्या होगा? और 4 बजे? 6 बजे? (ग) घड़ी की सुइयों द्वारा बनाए गए अन्य कोणों का अन्वेषण करें।

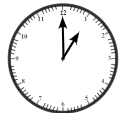
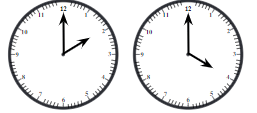
उत्तर: (क) घड़ी के चारों ओर 1 से 12 तक के नंबर्स समान दूरी पर लिखे गए हैं। 360 ÷ 12 = 30। इसलिए, दो लगातार नंबरों के बीच का कोण 30° है। 1 बजे, सुइयाँ 0 और 1 पर (लगातार नंबर) होती हैं। इसलिए उनके बीच का कोण 30° है। (ख) 2 बजे सुइयों के बीच का कोण = 2 × 30° = 60°। 4 बजे सुइयों के बीच का कोण = 4 × 30° = 120°। 6 बजे सुइयों के बीच का कोण = 6 × 30° = 180°। (ग) 5 बजे सुइयों के बीच का कोण = 5 × 30° = 150°। 7 बजे सुइयों के बीच का कोण = 7 × 30° = 210°। 8 बजे सुइयों के बीच का कोण = 8 × 30° = 240°।

प्रश्न 2: दरवाजे का कोण: क्या यह संभव है कि दरवाजे के खुलने की मात्रा को कोण के रूप में व्यक्त किया जाए? कोण का वर्टेक्स क्या होगा और कोण की भुजाएँ क्या होंगी? उत्तर: हाँ, यह संभव है कि दरवाजे के खुलने की मात्रा को कोण के रूप में व्यक्त किया जाए। दरवाजे का हिंज कोण का वर्टेक्स होगा। दीवार और दरवाजा कोण की भुजाएँ होंगे।

प्रश्न 3: विद्या झूले पर समय का आनंद ले रही है। वह देखती है कि जिस कोण से वह झूलने शुरू करती है, उस कोण के बढ़ने पर उसके झूले पर गति भी बढ़ती है। लेकिन कोण कहाँ है? क्या आप कोई कोण देख सकते हैं? उत्तर: हाँ, हम कोण देख सकते हैं और यह कोण रस्सी और पेड़ की शाखा के बीच है।

पृष्ठ 46

प्रश्न 4: यहाँ एक खिलौना है जिसमें तिरछे स्लैब इसके किनारों से जुड़े हुए हैं; जितने अधिक कोण या ढलान होंगे, गेंदें उतनी ही तेजी से रोल करेंगी। क्या कोणों का उपयोग स्लैब की ढलानों का वर्णन करने के लिए किया जा सकता है? प्रत्येक कोण की भुजाएँ क्या हैं? कौन सी भुजा दृश्य है और कौन सी नहीं? उत्तर: हाँ, कोणों का उपयोग स्लैब की ढलानों का वर्णन करने के लिए किया जा सकता है। तिरछा स्लैब और खिलौने के किनारों के लंबवत अदृश्य रेखा प्रत्येक कोण की दो भुजाएँ हैं। तिरछा स्लैब दृश्य है और खिलौने के किनारों के लिए लंबवत रेखा अदृश्य है।

प्रश्न 5: नीचे की छवियों पर ध्यान दें जहाँ एक कीड़ा और उसका घुमाया हुआ संस्करण है। क्या कोणों का उपयोग घुमाव की मात्रा का वर्णन करने के लिए किया जा सकता है? कैसे? कोण की भुजाएँ और शीर्षक क्या होंगे? संकेत: कीड़ों को छूने वाली क्षैतिज रेखा पर ध्यान दें। उत्तर: हाँ, कोणों का उपयोग कीड़े की प्रारंभिक और अंतिम स्थिति को देखकर घुमाव की मात्रा का वर्णन करने के लिए किया जा सकता है। क्षैतिज रेखा और स्वयं कीड़ा कोण की भुजाएँ होंगी। शीर्षक कीड़े के पिछले हिस्से पर होगा।

पृष्ठ 49

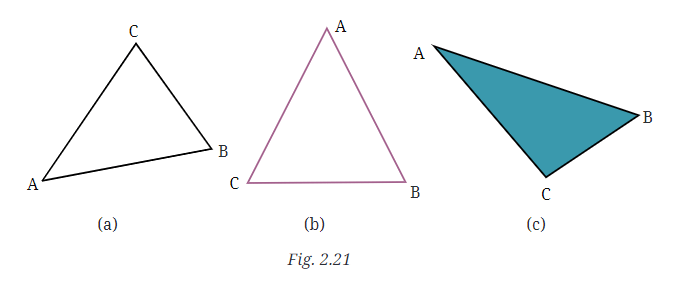
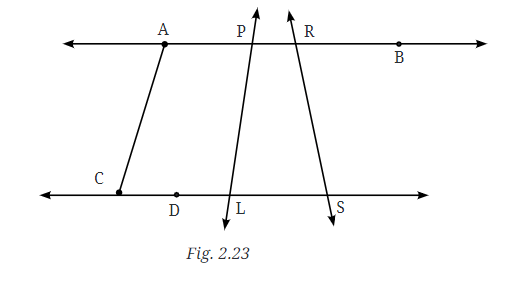
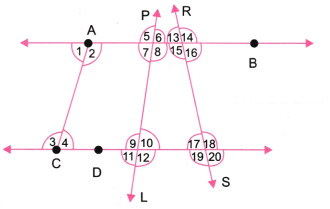
प्रश्न 1: चित्र 2.23 में, सभी संभव कोणों की सूची बनाएं। क्या आपने सभी को पाया? अब, सभी कोणों का अनुमान लगाएँ। फिर, प्रोट्रैक्टर से कोणों को मापें। अपने सभी नंबरों को एक तालिका में रिकॉर्ड करें। देखें कि आपके अनुमान वास्तविक मापों के कितने करीब हैं। उत्तर: दिए गए चित्र में 20 कोण हैं। अनुमान: ∠1 = ∠4 = 60°; ∠2 = ∠3 = 120°; वास्तविक माप से: ∠1 = ∠4 = 70°; ∠2 = ∠3 = 110°। अनुमानित माप वास्तविक मापों के काफी करीब थे।

पृष्ठ 50

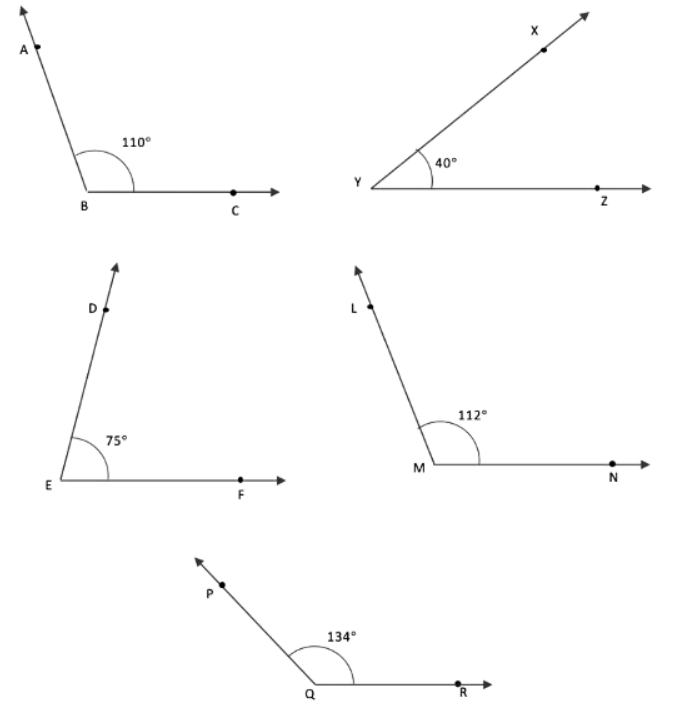
प्रश्न 2: एक प्रोट्रैक्टर का उपयोग करके निम्नलिखित डिग्री माप वाले कोण बनाएं:

• (क) 110º
• (ख) 40º
• (ग) 75º
• (घ) 112º
• (ङ) 134º

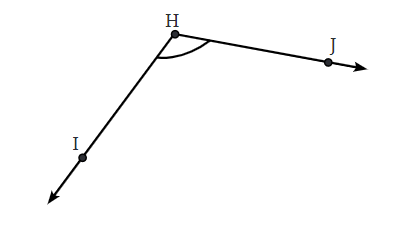
प्रश्न 3: एक ऐसा कोण बनाएं जिसका डिग्री माप निम्नलिखित कोण के समान है: इसके साथ, वह चरण लिखें जिन्हें आपने कोण बनाने के लिए अनुसरण किया।

• चरण 1: दिए गए कोण को मापें (∠IHJ = 120°)
• चरण 2: प्रोट्रैक्टर का उपयोग करके ∠ABC = 120° बनाएं।

पृष्ठ 51 और 52

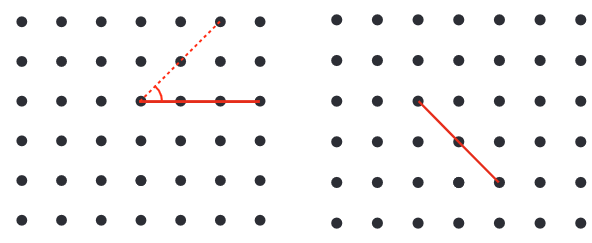
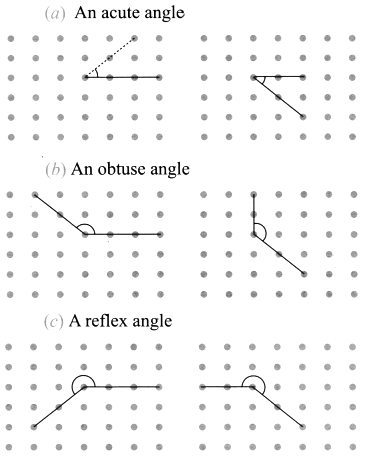
प्रश्न 1: नीचे दिए गए प्रत्येक ग्रिड में, A को चित्र में अन्य ग्रिड बिंदुओं से सीधी रेखा से जोड़ें ताकि:

• (क) एक तीजकोण प्राप्त करें
• (ख) एक विषम कोण प्राप्त करें
• (ग) एक रिफ्लेक्स कोण प्राप्त करें

इच्छित कोणों को दर्शाने के लिए वक्र के साथ चिह्नित करें। एक आपके लिए किया गया है। उत्तर:

प्रश्न 2: एक प्रोट्रैक्टर का उपयोग करके प्रत्येक कोण का माप ज्ञात करें। फिर प्रत्येक कोण को तिजकोण, विषम, समकोण, या रिफ्लेक्स के रूप में वर्गीकृत करें।

• (क) ∠PTR
• (ख) ∠PTQ
• (ग) ∠PTW
• (घ) ∠WTP

• (क) ∠PTR = 300 रिफ्लेक्स
• (ख) ∠PTQ = 60° तिजकोण
• (ग) ∠PTW = 105° विषम
• (घ) ∠WTP = 225° रिफ्लेक्स

पृष्ठ 53

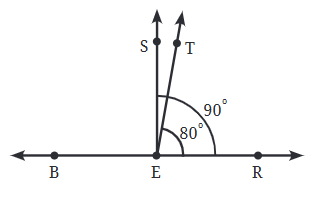
आओ खोजें: प्रश्न: इस चित्र में, ∠TER = 80º। ∠BET का माप क्या है? ∠SET का माप क्या है? उत्तर: ∠BET = 180º - ∠TER = 180º - 80º = 100º ∠SET = ∠SER - ∠TER = 90º - 80º = 10º

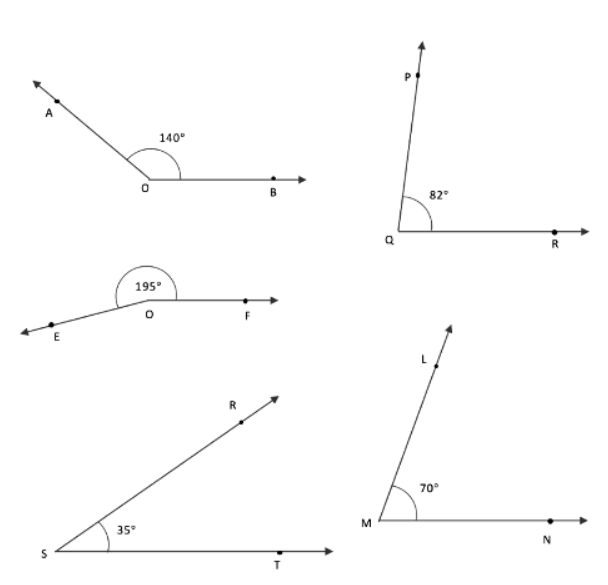
प्रश्न 1: निम्नलिखित डिग्री माप वाले कोण बनाएं:

• (क) 140°
• (ख) 82°
• (ग) 195°
• (घ) 70°
• (ङ) 35°

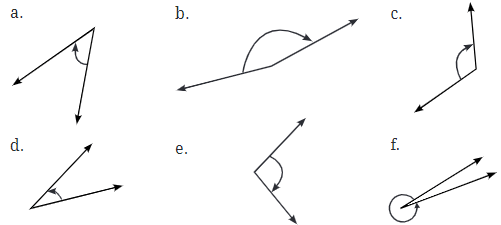
प्रश्न 2: प्रत्येक कोण का आकार अनुमानित करें और फिर इसे एक प्रोट्रैक्टर से मापें: इन कोणों को तिजकोण, समकोण, विषम या रिफ्लेक्स कोण के रूप में वर्गीकृत करें।

• (क) 45° तिजकोण
• (ख) 150° विषम
• (ग) 120° विषम
• (घ) 30° तिजकोण
• (ङ) 95° विषम
• (च) 350° रिफ्लेक्स

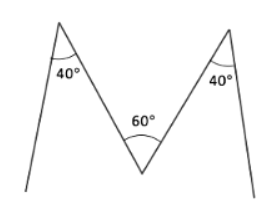
व्याख्या: 'M' के प्रत्येक पक्ष को आधार के साथ 40° का कोण बनाना चाहिए, और शीर्ष पर केंद्रीय कोण 60° होना चाहिए।

प्रश्न 5: 'Y' अक्षर को इस प्रकार खींचें कि बने हुए तीन कोण 150°, 60° और 150° हों। उत्तर:

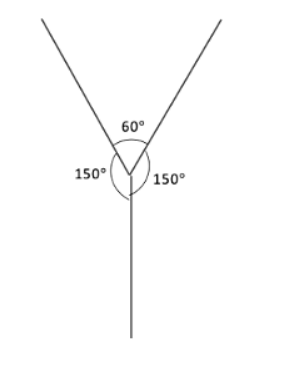
व्याख्या: शीर्ष पर कोण चौड़े (150°) होने चाहिए, जबकि आधार पर केंद्रीय कोण संकरा (60°) होना चाहिए।

पृष्ठ 54

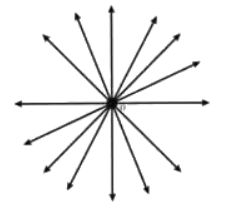
प्रश्न 6: अशोक चक्र में 24 spoke हैं। एक दूसरे के पास के दो spokes के बीच का कोण क्या है? दो spokes के बीच बना सबसे बड़ा तीव्र कोण क्या है? उत्तर: अशोक चक्र में 24 spokes हैं और कुल 360° हैं। दो spokes के बीच का कोण = 360°/24 = 15°। दो spokes के बीच संभावित कोण 15°, 30°, 45°, 60°, 75° हैं। इसलिए, दो spokes के बीच बना सबसे बड़ा तीव्र कोण 75° है।

प्रश्न 7: पहेली: मैं एक तीव्र कोण हूँ। यदि आप मेरे माप को दो गुना करते हैं, तो आपको एक तीव्र कोण मिलेगा। यदि आप मेरे माप को तीन गुना करते हैं, तो आपको फिर से एक तीव्र कोण मिलेगा। यदि आप मेरे माप को चार गुना (चार बार) करते हैं, तो आपको फिर से एक तीव्र कोण मिलेगा! लेकिन यदि आप मेरे माप को 5 गुना करते हैं, तो आपको एक obtuse कोण मिलेगा। मेरे माप के लिए संभावनाएँ क्या हैं? उत्तर: मान लीजिए कि कोण का माप m है। फिर 5 × m > 90 लेकिन 4 × m < 90="" या="" m="" /> 90/5 और m < 90/4।="" इसलिए="" m="" /> 18 लेकिन m < 22½।="" इस="" प्रकार,="" कोण="" का="" माप="" 19°,="" 20°="" या="" 21°="" />