Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > Unit Test (Solutions) रेखाएँ और कोण

Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

समय: 1 घंटा अधिकतम अंक: 30 सभी प्रश्नों का उत्तर दें। प्रश्न संख्या 1 से 5 में 1 अंक प्रत्येक का है। प्रश्न संख्या 6 से 8 में 2 अंक प्रत्येक का है। प्रश्न संख्या 9 से 11 में 3 अंक प्रत्येक का है। प्रश्न संख्या 12 और 13 में 5 अंक प्रत्येक का है।

Q1: घड़ी के घंटे के हाथ के 3 बजे से 6 बजे तक बढ़ने पर बने कोण को मापें। (1 अंक) उत्तर: 90° घंटे का हाथ 3 से 6 तक बढ़ता है, जो 3 घंटे को कवर करता है। प्रत्येक घंटे का प्रतिनिधित्व 30° करता है, इसलिए कुल कोण 3 × 30° = 90° है।

Q2: एक किरण बिंदु M से शुरू होती है और बिंदु N से गुजरती है। यदि बिंदु P बिंदु N के दाएं उसी रेखा पर है, तो इन बिंदुओं का उपयोग करते हुए इस किरण को क्या कहा जाता है? (1 अंक) उत्तर: किरण MP एक किरण एक बिंदु (इस मामले में M) से शुरू होती है और दूसरे बिंदु (N) से गुजरती है, जो बिंदु P के माध्यम से अनंत तक बढ़ती है, इसलिए इसे किरण MP कहा जाता है।

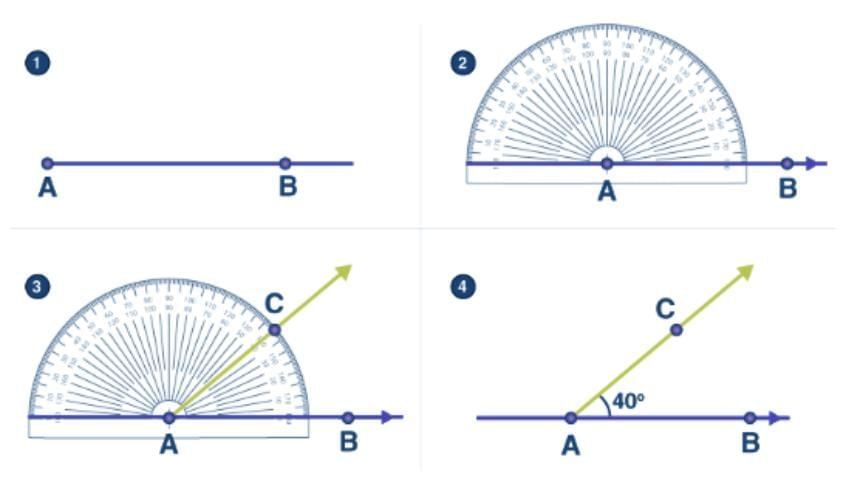
Q3: एक प्रोट्रैक्टर का उपयोग करके 40° का कोण बनाएं। (1 अंक) उत्तर: 180° - (35° 65°) = 80°

Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Q4: 10:00 बजे घड़ी के हाथों द्वारा बने कोण (तीव्र, समकोण, उभयकोण, या सीधा) को पहचानें। (1 अंक) उत्तर: तीव्र कोण 10:00 बजे, घंटे का हाथ 10 पर है और मिनट का हाथ 12 पर है। प्रत्येक घंटे के मार्किंग के बीच का कोण 30° है। 10 से 12 तक 2 घंटे के विभाजन हैं: 2 × 30° = 60°। चूंकि 60° 90° से कम है, यह एक तीव्र कोण है।

Q5: उस कोण का माप क्या है जो समकोण के माप का तीन गुना है? (1 अंक) उत्तर: 270° एक समकोण 90° है। इसलिए, समकोण का तीन गुना 3 × 90° = 270° है।

Q6: दो रेखाएं मिलती हैं और 150° का कोण बनाती हैं। उस इंटरसेक्शन पर सभी कोणों के माप क्या हैं? (2 अंक) उत्तर: कोण 150°, 30°, 150°, 30° हैं। विपरीत कोण समान होते हैं, इसलिए दो कोण 150° हैं और अन्य दो 30° हैं, क्योंकि 180° − 150° = 30°। 180° - 150° = 30°।

प्रश्न 7: 5 सेमी का एक रेखा खंड खींचें। इसके मध्य बिंदु पर, 4 सेमी का एक लंबवत रेखा खंड खींचें। इन दोनों रेखा खंडों के बीच कौन सा प्रकार का कोण बनता है? (2 अंक)
उत्तर: समकोण (90°) एक लंबवत रेखा मूल रेखा खंड के साथ समकोण बनाती है।

प्रश्न 8: क्या दो obtuse कोण पूरक हो सकते हैं? समझाएं क्यों या क्यों नहीं। (2 अंक)
उत्तर: नहीं, दो obtuse कोण पूरक नहीं हो सकते। एक obtuse कोण 90° से अधिक होता है। दो obtuse कोणों का योग 180° से अधिक होगा, जिससे वे पूरक नहीं बनते।

प्रश्न 9: एक कोण बाइसेक्टर ∠XYZ को दो कोणों, ∠XYB और ∠BYZ में बांटती है। यदि ∠XYZ = 90°, तो ∠XYB और ∠BYZ ज्ञात करें। (3 अंक)
उत्तर: ∠XYB = 45°, ∠BYZ = 45°। कोण बाइसेक्टर ∠XYZ को समान रूप से दो कोणों में बांटती है, इसलिए प्रत्येक 90° ÷ 2 = 45° होगा।

प्रश्न 10: प्रोट्रैक्टर का उपयोग करके 75° का कोण बनाएं और इसे ∠ABC के रूप में लेबल करें। उठाए गए कदमों का वर्णन करें। (3 अंक)
उत्तर:

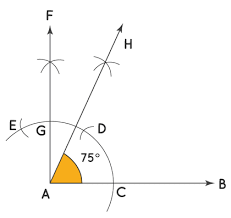
चरण 1: एक किरण AB खींचें। A को केंद्र मानकर और किसी भी त्रिज्या के साथ, एक आर्क खींचें जो AB को C पर काटता है।
चरण 2: C को केंद्र मानकर और समान त्रिज्या के साथ, हम एक आर्क खींचते हैं जो पहले आर्क को D पर काटता है, और D को केंद्र मानकर और समान त्रिज्या के साथ, एक आर्क खींचते हैं जो पहले आर्क को E पर काटता है।
चरण 3: E और D को केंद्र मानकर और समान त्रिज्या के साथ, हम दो आर्क खींचते हैं जो एक दूसरे को F पर काटते हैं। AF को जोड़ें। रेखा AF रेखा खंड AB के साथ 90° बनाती है।
चरण 4: उस बिंदु को चिह्नित करें जहां रेखा AF अर्ध-चक्राकार आर्क को G पर छूती है। अब G और D को केंद्र मानकर, फिर से दो आर्क खींचें जो एक दूसरे को H पर काटते हैं। अब हम AH को जोड़ते हैं। ∠HAB = 75°।

75° के कोण का निर्माण नीचे दिखाया गया है।

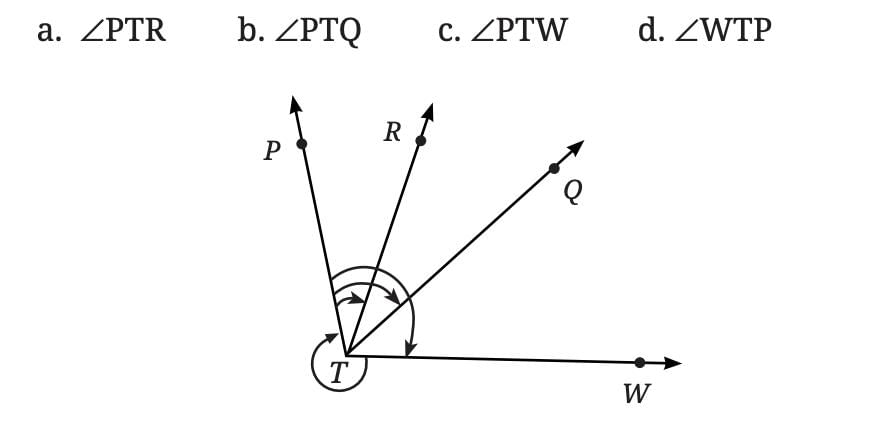
प्रश्न 11: एक प्रोट्रैक्टर का उपयोग करके प्रत्येक कोण का मापन करें। फिर प्रत्येक कोण को तीखा, obtuse, सही, या reflex के रूप में वर्गीकृत करें। (5 अंक)

उत्तर: ∠ABD = 90°

∠PTR = 300° reflex
∠PTQ = 60° acute
∠PTW = 105° obtuse
∠WTP = 225° reflex

25° + 65° = 90°

Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 12: एक त्रिकोण में कोणों का अनुपात 1:2:3 है। सभी तीन कोणों का मापन करें। (5 अंक)

उत्तर: 30°, 60°, 90°

मान लें कि कोण x, 2x, और 3x हैं। एक त्रिकोण में कोणों का योग 180° होता है। इसलिए, x + 2x + 3x = 180° ⇒ 6x = 180° ⇒ x = 30°

इस प्रकार, कोण 30°, 60°, और 90° हैं।

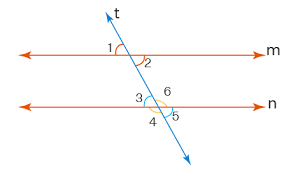
प्रश्न 13: दिए गए दो समानांतर रेखाएँ एक ट्रांसवर्सल द्वारा काटी जाती हैं, जिसमें एक जोड़ी समकोणों का मापन 110° है, सभी अन्य कोणों का मापन खोजें। (5 अंक)

उत्तर: दिए गए चित्र में, रेखाएँ m और n समानांतर हैं, और रेखा t एक ट्रांसवर्सल है। प्रश्न में कहा गया है कि एक जोड़ी समकोण 110° है।

चित्र के अनुसार: कोण 2, कोण 6 के समकक्ष है, मानते हुए कि कोण 2 110° है जैसा कि मूल प्रश्न में है।

कोण 2 और कोण 6 = 110° (समकक्ष कोण)
कोण 1 = 110° (कोण 2 के लिए वर्टिकल विपरीत कोण)
कोण 3 = 70° (कोण 2 के साथ रेखीय जोड़ी)
कोण 5 = 70° (कोण 3 के लिए समकक्ष कोण)
कोण 4 = 70° (कोण 5 के लिए वर्टिकल विपरीत)

इस प्रकार, आपके पास हैं:

कोण 1 = 110°
कोण 2 = 110°
कोण 3 = 70°
कोण 4 = 70°
कोण 5 = 70°
कोण 6 = 110°

ये गणनाएँ सुनिश्चित करती हैं कि ट्रांसवर्सल द्वारा बनाए गए सभी कोण दो समानांतर रेखाओं के साथ ज्यामितीय नियमों के अनुसार संगत हैं।

The document Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: Unit Test (Solutions) रेखाएँ और कोण for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for Unit Test (Solutions) रेखाएँ और कोण have been prepared according to the Class 6 exam syllabus. Information about Unit Test (Solutions) रेखाएँ और कोण covers topics like and Unit Test (Solutions) रेखाएँ और कोण Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Unit Test (Solutions) रेखाएँ और कोण.

Introduction of Unit Test (Solutions) रेखाएँ और कोण in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & Unit Test (Solutions) रेखाएँ और कोण in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about Unit Test (Solutions) रेखाएँ और कोण

In this doc you can find the meaning of Unit Test (Solutions) रेखाएँ और कोण defined & explained in the simplest way possible. Besides explaining types of Unit Test (Solutions) रेखाएँ और कोण theory, EduRev gives you an ample number of questions to practice Unit Test (Solutions) रेखाएँ और कोण tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Extra Questions

Semester Notes

Objective type Questions

Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Important questions

shortcuts and tricks

Viva Questions

practice quizzes

Unit Test (Solutions) रेखाएँ और कोण | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

ppt

Sample Paper

Summary

Exam

Previous Year Questions with Solutions

MCQs

study material

Free

video lectures

past year papers

pdf

mock tests for examination

;

Additional Information about Unit Test (Solutions) रेखाएँ और कोण for Class 6 Preparation

Unit Test (Solutions) रेखाएँ और कोण Free PDF Download

The Unit Test (Solutions) रेखाएँ और कोण is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Unit Test (Solutions) रेखाएँ और कोण now and kickstart your journey towards success in the Class 6 exam.

Importance of Unit Test (Solutions) रेखाएँ और कोण

The importance of Unit Test (Solutions) रेखाएँ और कोण cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Unit Test (Solutions) रेखाएँ और कोण Notes

Unit Test (Solutions) रेखाएँ और कोण Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Unit Test (Solutions) रेखाएँ और कोण. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Unit Test (Solutions) रेखाएँ और कोण Notes on EduRev are your ultimate resource for success.

Unit Test (Solutions) रेखाएँ और कोण Class 6 Questions

The "Unit Test (Solutions) रेखाएँ और कोण Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Unit Test (Solutions) रेखाएँ और कोण on the App

Students of Class 6 can study Unit Test (Solutions) रेखाएँ और कोण alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Unit Test (Solutions) रेखाएँ और कोण, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Unit Test (Solutions) रेखाएँ और कोण is prepared as per the latest Class 6 syllabus.

Education Revolution