संख्या खेल Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

परिचय

संख्याएँ हमारे दैनिक जीवन में एक महत्वपूर्ण भूमिका निभाती हैं, जो हमें विभिन्न कार्यों को व्यवस्थित और प्रबंधित करने में मदद करती हैं। हम इनका उपयोग गणना के लिए करते हैं, साथ ही रोज़मर्रा की समस्याओं को हल करने के लिए मूलभूत क्रियाएँ जैसे जोड़ना, घटाना, गुणा और भाग करना।

संख्याओं के उपयोग के उदाहरण:

• समय बताना: हम घड़ी पर समय पढ़ने के लिए संख्याओं का उपयोग करते हैं।
• खरीदारी: संख्याएँ वस्तुओं की कुल लागत की गणना और पैसे का प्रबंधन करने में उपयोग होती हैं।
• पकवान बनाना: व्यंजनों में अक्सर सामग्री के विशेष माप की आवश्यकता होती है, जिसमें संख्याएँ शामिल होती हैं।
• यात्रा करना: संख्याएँ यात्रा के दौरान दूरी, गति और समय को समझने में मदद करती हैं।
• खेल: स्कोर, समय सीमाएँ, और खिलाड़ी की सांख्यिकी सभी संख्याओं से संबंधित होती हैं।

संख्याएँ हमें बातें बता सकती हैं

कल्पना कीजिए कि छात्रों की एक पंक्ति स्कूल की दौड़ के लिए खड़ी है। प्रत्येक छात्र एक संख्या घोषित करता है, जो उनकी पंक्ति में स्थिति के बारे में कुछ दर्शाती है। आइए देखें कि ये संख्याएँ क्या अर्थ रख सकती हैं:

• अगर एक छात्र के बगल में एक तेज़ धावक है तो वह '1' कहता है।
• अगर उसके दोनों पड़ोसी तेज़ हैं तो वह '2' कहता है।
• अगर उसके बगल में कोई भी तेज़ नहीं है तो वह '0' कहता है।

इस मामले में, प्रत्येक छात्र यह गिन रहा है कि उनके पड़ोसी कितने तेज़ धावक हैं।

सुपरसेल

एक सुपरसेल एक ऐसा संख्या है जो एक ग्रिड में अपने सभी पड़ोसी संख्याओं से बड़ी होती है। एक सेल के पड़ोसी वह संख्याएँ हैं जो सीधे उसके बाईं, दाईं, ऊपर और नीचे होती हैं। मान लीजिए कि हमारे पास संख्याओं का एक ग्रिड है, और हमारा कार्य सुपरसेल्स को खोजना है।

संख्याओं के पैटर्न संख्या रेखा पर

आइए कुछ संख्याओं को संख्या रेखा पर रखने का अभ्यास करते हैं। कल्पना करें कि आपके पास निम्नलिखित संख्याएँ हैं: 2180, 2754, 1500, 3600, 9950, 9590, 1050, 3050, 5030, 5300, और 8400। इन संख्याओं को संख्या रेखा पर सही ढंग से रखा जाना चाहिए। यहाँ एक बुनियादी संख्या रेखा है जो आपकी कल्पना में मदद करेगी:

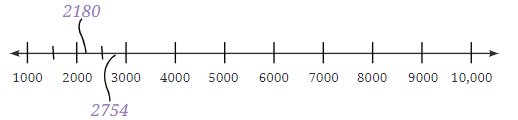
• 2180 को 2000 के बाद लेकिन 3000 से पहले रखा जाएगा।
• 9950 लगभग 10,000 के बहुत करीब होगा।
• 3050 बस 3000 के बाद होगा, और इसी तरह।

अंक के साथ खेलना

जब हम संख्याओं की गिनती शुरू करते हैं, तो हम उन्हें क्रम में लिखते हैं: 1, 2, 3, और इसी तरह। चलिए देखते हैं कि विभिन्न अंक लंबाई के साथ कितनी संख्याएँ हैं।

1-अंक की संख्याएँ: ये संख्याएँ 1 से 9 तक होती हैं, इसलिए 9 एक-अंक की संख्याएँ हैं।

2-अंक की संख्याएँ: ये संख्याएँ 10 से 99 तक होती हैं। यह जानने के लिए कि कितनी हैं:

• सबसे छोटी दो-अंक की संख्या (10) को सबसे बड़ी (99) से घटाएँ और 1 जोड़ें।
• 99 - 10 + 1 = 90
• तो, 90 दो-अंक की संख्याएँ हैं।

3-अंक की संख्याएँ: ये संख्याएँ 100 से 999 तक होती हैं।

• 999 - 100 + 1 = 900
• तो, 900 तीन-अंक की संख्याएँ हैं।

4-अंक की संख्याएँ: ये संख्याएँ 1000 से 9999 तक होती हैं।

• 9999 - 1000 + 1 = 9000
• तो, 9000 चार-अंक की संख्याएँ हैं।

5-अंक की संख्याएँ: ये संख्याएँ 10,000 से 99,999 तक होती हैं।

नंबर 99,999 से 10,000 तक के बीच में 90,000 पाँच अंकों के नंबर हैं।

• 99,999 - 10,000 1 = 90,000

संख्याओं के अंकों का योग

राजत ने एक दिलचस्प पैटर्न देखा: कभी-कभी, जब आप विभिन्न संख्याओं के अंकों को जोड़ते हैं, तो योग समान होता है। उदाहरण के लिए:

• 68: 6 + 8 = 14
• 176: 1 + 7 + 6 = 14
• 545: 5 + 4 + 5 = 14

इन सभी संख्याओं का अंक योग 14 है!

अंक जासूस

माही को एक जिज्ञासापूर्ण विचार आया: 1 से 100 या यहाँ तक कि 1 से 1000 तक सभी संख्याओं को लिखते समय अंक ‘7’ कितनी बार दिखाई देता है?

• 1 से 100: अंक ‘7’ 7वें, 17वें, 27वें, 37वें, 47वें, 57वें, 67वें, 70-79 (10 बार), और 87वें, 97वें में दिखाई देता है। कुल मिलाकर यह 20 बार है।
• 1 से 1000: अंक ‘7’ तीन स्थानों (सौ, दस और इकाई) में अधिक बार दिखाई देगा। प्रत्येक स्थान के लिए गणना करने में यह देखा जाता है कि ‘7’ प्रत्येक अंक स्थान में कितनी बार आता है:
  • इकाई स्थान: 100 बार (7, 17, 27...997)
  • दस स्थान: 100 बार (70-79 हर सौ में)
  • सौ स्थान: 100 बार (700-799)

इसलिए, अंक ‘7’ 1 से 1000 के बीच कुल 300 बार दिखाई देता है।

सुंदर पलिंड्रोमिक पैटर्न

पलिंड्रोमिक संख्याएँ वे संख्याएँ हैं जो आगे और पीछे दोनों ओर से पढ़ने पर समान होती हैं। उदाहरण के लिए, संख्याएँ 66, 848, 575, 797, और 1111 सभी पलिंड्रोम हैं क्योंकि इन्हें बाएँ से दाएँ या दाएँ से बाएँ पढ़ने पर एक समान दिखती हैं।

3-अंक के पलिंड्रोम बनाना

चलो देखें कि 1, 2, और 3 अंकों का उपयोग करके सभी संभावित 3-अंक के पलिंड्रोम कैसे बनाए जाते हैं। एक 3-अंक का पलिंड्रोम का पहला और तीसरा अंक समान होता है। यहाँ पर वे कैसे दिखते हैं:

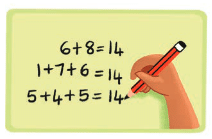
• 121: पहले और आखिरी अंक 1 हैं, और मध्य अंक 2 है।
• 131: पहले और आखिरी अंक 1 हैं, और मध्य अंक 3 है।
• 212: पहले और आखिरी अंक 2 हैं, और मध्य अंक 1 है।
• 232: पहले और आखिरी अंक 2 हैं, और मध्य अंक 3 है।
• 313: पहले और आखिरी अंक 3 हैं, और मध्य अंक 1 है।
• 323: पहले और आखिरी अंक 3 हैं, और मध्य अंक 2 है।

ये सभी संभव 3-अंक के पैलिंड्रोम हैं जिन्हें आप केवल अंकों 1, 2, और 3 का उपयोग करके बना सकते हैं।

रिवर्स-और-ऐड पैलिंड्रोम्स

अब, चलिए पैलिंड्रोम्स से संबंधित एक मजेदार गतिविधि, जिसे रिवर्स-और-ऐड विधि कहा जाता है, का पता लगाते हैं। यह कैसे काम करता है:

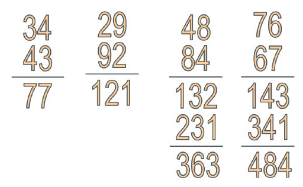
एक 2-अंक का नंबर शुरू करें। उदाहरण के लिए, 34 चुनते हैं।

संख्याओं के अंकों को पलटें: 34 का पलटाव 43 होता है।

मूल संख्या को उसके पलटाव से जोड़ें: 34 + 43 = 77

जांचें कि क्या परिणाम एक पैलिंड्रोम है। यदि है, तो आप समाप्त हो गए। यदि नहीं, तो नए नंबर को पलटें और फिर से जोड़ें।

आइए एक अलग संख्या, 47 के साथ एक और उदाहरण आजमाते हैं:

• 47 का पलटाव 74 है।
• इन्हें जोड़ें: 47 + 74 = 121।
• चूंकि 121 एक पैलिंड्रोम है, हम यहां रुकते हैं।

आइए 89 के साथ आजमाते हैं:

• 89 का पलटाव 98 है।
• इन्हें जोड़ें: 89 + 98 = 187 (पैलिंड्रोम नहीं है, इसलिए जारी रखें)।
• 187 का पलटाव 781 है।
• इन्हें जोड़ें: 187 + 781 = 968 (पैलिंड्रोम नहीं है, इसलिए जारी रखें)।
• 968 का पलटाव 869 है।
• इन्हें जोड़ें: 968 + 869 = 1837 (अभी भी पैलिंड्रोम नहीं है)।

इस मामले में, आप तब तक प्रक्रिया दोहराते रहेंगे जब तक कि आपको एक पैलिंड्रोम नहीं मिल जाता। कुछ संख्याएं पैलिंड्रोम बनने में कई चरण लेती हैं, जबकि अन्य कभी ऐसा नहीं कर सकतीं!

पहेली का समय

यहाँ एक मजेदार पहेली है:

मैं एक 5-अंकीय पैलिंड्रोम हूं। मैं एक सम संख्या हूं। मेरा 't' अंक (तीसरा अंक) मेरे 'u' अंक (दूसरा अंक) का आधा है। मेरा 'h' अंक (चौथा अंक) मेरे 't' अंक का तीन गुना है।

मैं कौन हूं? _______

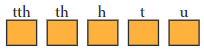
उत्तर: 5-अंकीय सम पैलिंड्रोम संख्या: 68486 शब्दों में: अठारह हजार चार सौ छियासी।

काप्रेकर का जादुई नंबर

D.R. काप्रेकर एक गणित के शिक्षक थे जो देवलाली, महाराष्ट्र से थे, और उन्हें संख्याओं से गहरा प्रेम था। उन्होंने संख्याओं में कई रोचक पैटर्न खोजे जो पहले कभी नहीं देखे गए थे। उनकी सबसे प्रसिद्ध खोजों में से एक काप्रेकर स्थिरांक है, जो 4-अंकीय संख्याओं से जुड़ा एक जादुई नंबर है।

जादू खोजने के चरण:

किसी भी 4-अंकीय संख्या का चयन करें (जैसे, 6382).

अंक को इस तरह व्यवस्थित करें कि सबसे बड़ा संभव नंबर बने। इसे A कहें।

• 6382 के लिए, सबसे बड़ा नंबर है 8632.

अंक को इस तरह व्यवस्थित करें कि सबसे छोटा संभव नंबर बने। इसे B कहें।

• 6382 के लिए, सबसे छोटा नंबर है 2368.

B को A से घटाकर एक नया नंबर प्राप्त करें, C।

• घटाएं: 8632 - 2368 = 6264.

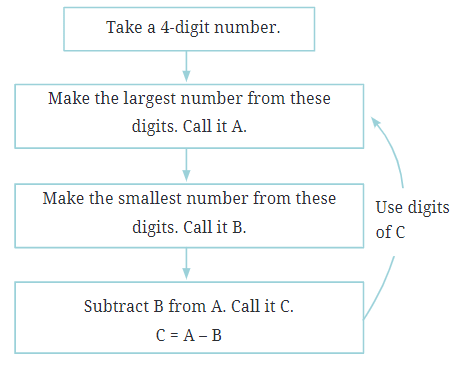
अगला क्या होता है?

संख्या C लें और प्रक्रिया को दोहराएं: 6264 से शुरू करें:

• सबसे बड़ा नंबर (A): 6642
• सबसे छोटा नंबर (B): 2466
• घटाएं: 6642 - 2466 = 4176

4176 के साथ जारी रखें:

• सबसे बड़ा नंबर (A): 7641
• सबसे छोटा नंबर (B): 1467
• घटाएं: 7641 - 1467 = 6174

आप चाहे जिस भी 4-अंकीय संख्या से शुरू करें, यदि आप इन चरणों को दोहराते हैं, तो आप हमेशा अंततः 6174 संख्या तक पहुँचेंगे। इस संख्या को काप्रेकर स्थिरांक कहा जाता है।

यदि आप समान चरणों का पालन करते हुए 3-अंकों के संख्याओं के साथ काम करते हैं, तो आप पाएंगे कि संख्या 495 दोहराना शुरू करती है। यह 3-अंकों के संख्याओं के लिए कापरेकर स्थिरांक है।

घड़ी और कैलेंडर संख्याएँ

घड़ियाँ और कैलेंडर केवल समय या तिथि बताने के उपकरण नहीं हैं; इनमें अपनी संख्याओं में छिपे हुए रोचक पैटर्न भी होते हैं।

घड़ी के पैटर्न

12-घंटे की घड़ी समय में पैटर्न खोजने के लिए रोचक अवसर प्रस्तुत करती है। उदाहरण के लिए:

• 4:44: यह एक समय है जहाँ सभी अंक समान हैं।
• 10:10: यहाँ, अंक एक दर्पण के समान दोहराते हैं।
• 12:21: यह समय पलिंड्रोमिक है, जिसका अर्थ है कि इसे आगे और पीछे पढ़ने पर समानता होती है।

अन्य पैटर्न खोजना

• 1:11: 4:44 के समान, सभी अंक समान हैं।
• 2:22: समान अंकों का एक और उदाहरण।
• 3:33: दोहराते अंकों का पैटर्न जारी रहा।
• 5:55: इसी प्रारूप का पालन करता है।
• 11:11: एक प्रसिद्ध समय, जो अक्सर अपनी समरूपता के लिए नोट किया जाता है।

इन सीधे उदाहरणों के अलावा, आप अन्य रोचक पैटर्न भी खोज सकते हैं जैसे:

• 12:12: एक समय जहाँ घंटे और मिनट के अंक समान संख्या को दोहराते हैं।
• 2:20: घंटे का अंक और मिनट के पहले अंक मेल खाते हैं।
• 5:05: घंटे का अंक और मिनट के अंतिम अंक समान हैं।

ये पैटर्न देखना मजेदार हो सकता है और दिखाते हैं कि समय देखना जैसे सामान्य कार्य में भी छिपी हुई संख्यात्मक सुंदरता हो सकती है।

कैलेंडर पैटर्न

कुछ विशेष तिथियाँ इस कारण से उभरती हैं कि उनके अंकों में दोहराव या कोई विशेष अनुक्रम होता है। उदाहरण के लिए, 20/12/2012 रोचक है क्योंकि अंकों 2, 0, 1, और 2 का दोहराव होता है। इस प्रकार का पैटर्न अन्य तिथियों में भी पाया जा सकता है:

02/10/2001: यहाँ, अंक 2, 0, 1 दोहराते हैं, लेकिन एक अलग क्रम में।

12/02/2001: इसी तरह का दोहराने वाला पैटर्न देखा जाता है।

10/02/2010: अंक 1, 0, 2, और 0 प्रकट होते हैं।

• ये तिथियाँ हमारी ध्यान आकर्षित करती हैं क्योंकि इनमें समmetry या दोहराव होता है, जिससे ये यादगार बन जाती हैं।

पलिंड्रोमिक तिथियाँ जैसे 11/02/2011

पलिंड्रोमिक तिथियाँ विशेष होती हैं क्योंकि इन्हें आगे और पीछे से पढ़ने पर एक समान होती हैं। उदाहरण के लिए:

• 02/02/2020: यह तिथि पूरी तरह से पलिंड्रोमिक है।
• 11/11/2011: एक तिथि जहाँ सभी अंक समान हैं और पूरी तिथि एक पलिंड्रोम है।
• 21/02/2012: एक और पलिंड्रोमिक तिथि जिसमें एक अलग क्रम होता है।

ये तिथियाँ दुर्लभ हैं और अक्सर अपनी सममिति के कारण विशेष या भाग्यशाली मानी जाती हैं।

कैलेंडर का पुन: उपयोग

जीवन के कैलेंडर के पुन: उपयोग के बारे में जिज्ञासा एक अच्छा सवाल है। सच्चाई यह है कि जबकि हमें आमतौर पर हर वर्ष एक नया कैलेंडर चाहिए होता है, कुछ वर्षों में बिल्कुल समान कैलेंडर साझा किए जा सकते हैं। इसका कारण यह है कि कैलेंडर तब दोहराता है जब सप्ताह के दिन समान तिथियों पर आते हैं, जो कई कारकों पर निर्भर करता है, जिसमें लीप वर्ष होना शामिल है।

एक लीप वर्ष हर 4 साल में होता है ताकि हमारा कैलेंडर सूर्य के चारों ओर पृथ्वी की कक्षा के साथ समन्वय में बना रहे। उदाहरण के लिए, वर्ष 2024 एक लीप वर्ष है, इसलिए फरवरी में 28 दिनों के बजाय 29 दिन होंगे।

मानसिक गणना

मध्य स्तंभ में अंक को जोड़कर किनारे पर अंक बनाए जाते हैं। यदि आवश्यक हो, तो आप मध्य में अंकों का कई बार उपयोग कर सकते हैं।

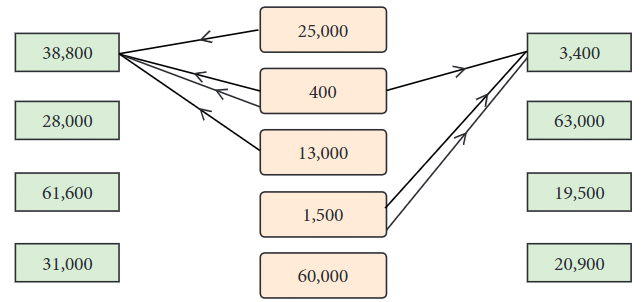
उदाहरण: 38,800

• गणना: 25,000 + 400 × 2 + 13,000।
• विभाजन: 25,000 से शुरू करें, 800 जोड़ें (400 दो बार), फिर 13,000 जोड़ें।

जोड़ना और घटाना

उदाहरण: 39,800

• गणना: 40,000 – 800 300 300।
• विवरण: 40,000 से शुरू करें, 800 घटाएं, फिर 300 को दो बार जोड़ें।

अंक और संचालन

यहाँ दो उदाहरण दिए गए हैं:

• दो 5-अंक वाले संख्याएं जोड़ना: 12,350 + 24,545 = 36,895
• दो 5-अंक वाले संख्याएं घटाना: 48,952 - 24,547 = 24,405

संख्याओं के पैटर्न के साथ खेलना

जब संख्याओं का एक सेट पैटर्न में व्यवस्थित होता है, तो अक्सर उन्हें अलग-अलग जोड़ने की तुलना में उन्हें जोड़ने के लिए तेज़ तरीके होते हैं। पैटर्न पहचानना गणनाओं को सरल और तेज़ बनाने में मदद कर सकता है।

पुस्तक से

इन चित्रों में, हमारे पास विभिन्न पैटर्न में व्यवस्थित संख्याएं हैं। कार्य यह है कि प्रत्येक पैटर्न में संख्याओं का कुल योग निकाला जाए। उन्हें एक-एक करके जोड़ने के बजाय, हम कुछ तरकीबें उपयोग कर सकते हैं ताकि योग जल्दी मिल सके। पैटर्न ए:

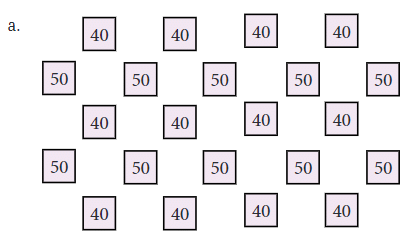
• शामिल संख्याएं: 40 और 50
• त्वरित गणना: ध्यान दें कि 50 केंद्र में है और इसे 40 के चारों ओर रखा गया है। संख्याओं को समूह बनाकर जोड़ें या गणना को तेज़ करने के लिए गुणन का उपयोग करें।
• समाधान:
  • शामिल संख्याएं: 40 और 50
  • चरण 1: संख्याओं की गणना करें: पैटर्न में हमारे पास 10 "50" और 12 "40" हैं।
  • चरण 2: संख्याओं को गुणा करें: 50 की संख्या को 50 से गुणा करें: 10 × 50 = 500।
  • 40 की संख्या को 40 से गुणा करें: 12 × 40 = 480।
  • चरण 3: उन्हें जोड़ें: 500 + 480 = 980।
  • अंतिम उत्तर: इस पैटर्न में संख्याओं का कुल योग 980 है।

पैटर्न ब:

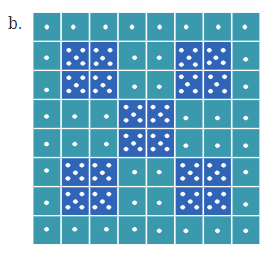
• पैटर्न शामिल: बिंदुओं से भरे छोटे चौकोर
• त्वरित गणना: चौकोरों की संख्या गिनें और प्रत्येक चौकोर में बिंदुओं की संख्या से गुणा करें। इससे आपको जल्दी से कुल बिंदुओं की संख्या मिल जाएगी।

समाधान:

• चरण 1: चौकोरों की गिनती करें। कुल 49 चौकोर हैं।
• चरण 2: चौकोरों के प्रकार पहचानें। 36 चौकोरों में 1-1 बिंदु है। 13 चौकोरों में 9-9 बिंदु हैं।
• चरण 3: बिंदुओं को गुणा और जोड़ें।
• 1 बिंदु वाले चौकोरों में बिंदु: 36 × 1 = 36
• 9 बिंदु वाले चौकोरों में बिंदु: 13 × 9 = 117
• चरण 4: उन्हें एक साथ जोड़ें: 36 + 117 = 153

अंतिम उत्तर: पैटर्न में कुल बिंदुओं की संख्या 153 है।

पैटर्न ग:

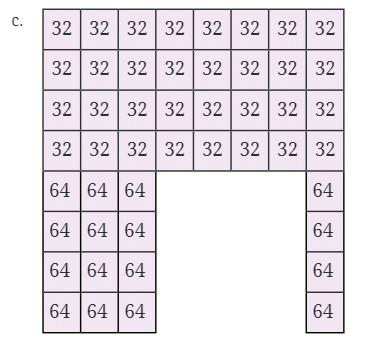
• संख्याएँ शामिल: 32 और 64
• त्वरित गणना: पैटर्न ज्यादातर 32 से बना है, लेकिन नीचे के भाग में 64 हैं। आप 32 और 64 की संख्या को अलग-अलग गुणा कर सकते हैं और फिर उन्हें जोड़ सकते हैं।

समाधान:

• संख्याएँ शामिल: 32 और 64
• चरण 1: संख्याओं की गिनती करें। पैटर्न में 28 "32" और 9 "64" हैं।
• चरण 2: संख्याओं को गुणा करें।
• 32 की संख्या को 32 से गुणा करें: 28 × 32 = 896
• 64 की संख्या को 64 से गुणा करें: 9 × 64 = 576
• चरण 3: उन्हें एक साथ जोड़ें: 896 + 576 = 1472

अंतिम उत्तर: इस पैटर्न में संख्याओं का कुल योग 1472 है।

पैटर्न d:

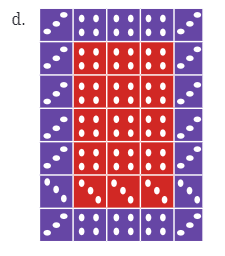
• शामिल संख्याएँ: अधिक वर्ग जिनमें बिंदु हैं
• त्वरित गणना: पैटर्न b के समान, बिंदुओं वाले वर्गों की गणना करें और गुणा करें। विभिन्न रंगों पर ध्यान दें, क्योंकि वे विभिन्न समूहों का प्रतिनिधित्व कर सकते हैं।
• समाधान:
  • चरण 1: वर्गों की पहचान करें
    • बैंगनी वर्गों में प्रत्येक में 4 बिंदु होते हैं।
    • लाल वर्गों में प्रत्येक में 6 बिंदु होते हैं।
  • चरण 2: वर्गों की संख्या गिनें
    • बैंगनी वर्ग: 20 वर्ग जिनमें 4 बिंदु हैं।
    • लाल वर्ग: 9 वर्ग जिनमें 6 बिंदु हैं।
  • चरण 3: बिंदुओं को गुणा करें
    • बैंगनी वर्गों में बिंदु: 20 × 4 = 80
    • लाल वर्गों में बिंदु: 9 × 6 = 54
  • चरण 4: उन्हें जोड़ें
    • 80 + 54 = 134
• अंतिम उत्तर: पैटर्न में कुल बिंदुओं की संख्या 134 है।

पैटर्न e:

• शामिल संख्याएँ: 15, 25, और 35
• त्वरित गणना: यह पैटर्न वृत्ताकार है। समान संख्याओं को समूहित करें और उनकी उपस्थिति की संख्या से गुणा करें।
• समाधान:
  • चरण 1: शामिल संख्याओं की पहचान करें
    • शामिल संख्याएँ: 15, 25, और 35।
  • चरण 2: प्रत्येक संख्या के बार-बार आने की संख्या गिनें
    • 15 15 बार आता है।
    • 25 16 बार आता है।
    • 35 13 बार आता है।
  • चरण 3: संख्याओं को उनकी उपस्थिति की संख्या से गुणा करें
    • 15 × 15 = 225
    • 25 × 16 = 400
    • 35 × 13 = 455
  • चरण 4: परिणाम जोड़ें
    • 225 + 400 + 455 = 1080
• अंतिम उत्तर: पैटर्न e के लिए कुल योग 1080 है।

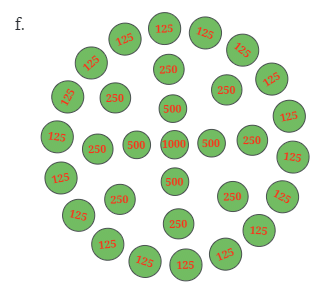
पैटर्न f:

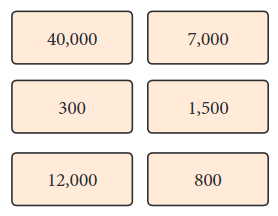
संख्याएँ शामिल: 125, 250, 500, 1000

• त्वरित गणना: संख्याएँ केंद्र की ओर बढ़ने पर बढ़ती हैं। सबसे पहले बाहरी वृत्तों को जोड़कर कुल का हिसाब लगाएँ।
• समाधान:
  • चरण 1: शामिल संख्याओं की पहचान करें: 125, 250, 500, और 1000।
  • चरण 2: प्रत्येक संख्या की उपस्थिति की गिनती करें:
    • 125, 12 बार।
    • 250, 9 बार।
    • 500, 6 बार।
    • 1000, 1 बार।
  • चरण 3: संख्याओं को उनकी उपस्थिति की संख्या से गुणा करें:
    • 125 × 12 = 1500
    • 250 × 9 = 2250
    • 500 × 6 = 3000
    • 1000 × 1 = 1000
  • चरण 4: परिणामों को जोड़ें:
    • 1500 + 2250 + 3000 + 1000 = 7750
• अंतिम उत्तर: पैटर्न f के लिए कुल योग 7750 है।

एक अनसुलझी पहेली - कोलत्ज़ अनुमान

कोलत्ज़ अनुमान एक दिलचस्प गणितीय अनुक्रम है जो अभी तक अनसुलझा है। अनुक्रम कैसे काम करते हैं, यहाँ बताया गया है:

अनुक्रम उदाहरण:

• अनुक्रम a: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1
• अनुक्रम b: 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
• अनुक्रम c: 21, 64, 32, 16, 8, 4, 2, 1
• अनुक्रम d: 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1

लागू किया गया नियम:

• सम संख्या: 2 से विभाजित करें।
• विषम संख्या: 3 से गुणा करें और 1 जोड़ें।
• दोहराएँ: परिणाम पर नियम को लगाते रहें।

प्रत्येक अनुक्रम, चाहे आप किस संख्या से शुरू करें, अंततः 1 तक पहुँचता है। यह अवलोकन कोलत्ज़ अनुमान का केंद्रीय भाग है।

सरल अनुमान

अनुमान तब मदद करता है जब आपको सटीक संख्या की आवश्यकता नहीं होती है और आप बस एक त्वरित विचार चाहते हैं। उदाहरण के लिए, यदि आप यह अनुमान लगा रहे हैं कि पुस्तकालय में कितनी किताबें हैं, तो आप जो देखते हैं उसके आधार पर अनुमान लगाते हैं न कि प्रत्येक को गिनते हैं।

उदाहरण 1: पुस्तकालय में किताबों की संख्या का अनुमान लगाना

• आप जानते हैं कि प्रत्येक शेल्फ पर लगभग 300 किताबें हैं।
• पुस्तकालय में 10 शेल्फ हैं।
• अनुमान: हर किताब को गिनने के बजाय, आप 300 को 10 से गुणा करते हैं और अनुमान लगाते हैं कि पुस्तकालय में लगभग 3,000 किताबें हैं।

उदाहरण 2: पार्टी में मेहमानों का अनुमान लगाना

• आप देखते हैं कि पार्टी में प्रत्येक टेबल पर लगभग 8 लोग हैं।
• कुल 12 टेबल हैं।
• अनुमान: 8 को 12 से गुणा करें ताकि यह अनुमान लगाया जा सके कि पार्टी में लगभग 100 लोग हैं।

खेल और जीतने की रणनीतियाँ

संख्याओं का उपयोग मजेदार खेलों में किया जा सकता है जहाँ आपको आगे की सोचने की आवश्यकता होती है और जीतने की योजना बनानी होती है।

खेल #1: 15 का खेल

नियम:

• खिलाड़ी बारी-बारी से 1 से 5 के बीच एक संख्या चुनते हैं।
• चुनी गई संख्या को एक चल रहे कुल में जोड़ा जाता है।
• पहला खिलाड़ी जो कुल को 15 तक पहुँचाता है, जीतता है।

जीतने की रणनीति:

• हमेशा जीतने के लिए, अपनी बारी के बाद कुल को 10 पर छोड़ने की कोशिश करें।
• उदाहरण के लिए, यदि आपका प्रतिद्वंद्वी ऐसी संख्याएँ चुनता है जो कुल को 9 बनाती हैं, तो आपको 1 चुनना चाहिए ताकि यह 10 हो जाए। इस तरह, आप खेल को नियंत्रित कर सकते हैं और अंततः 15 तक पहुँच सकते हैं।

खेल #2: 50 का खेल

• पहला खिलाड़ी 1 से 7 के बीच एक संख्या चुनता है।
• खिलाड़ी बारी-बारी से 1 से 7 के बीच एक संख्या जोड़ते हैं।
• पहला खिलाड़ी जो कुल को 50 तक पहुँचाता है, जीतता है।

• चल रहे कुल को महत्वपूर्ण संख्याओं जैसे 43, 36, 29, या 22 पर लाने का प्रयास करें।
• यदि आपका प्रतिद्वंद्वी कुल को 42 पर छोड़ता है, तो आपको 1 जोड़कर इसे 43 बनाना चाहिए। इससे आपको खेल जीतने का लाभ मिलेगा।

अपने स्वयं के खेल के विविधताएँ बनाना