यूनिट टेस्ट प्रश्न और समाधान: संख्या खेल - Class 6 PDF Download

समय: 1 घंटा म.म. 20

सभी प्रश्नों का उत्तर दें।

• प्रश्न संख्या 1 से 5 तक प्रत्येक 1 अंक का है।
• प्रश्न संख्या 6 से 8 तक प्रत्येक 2 अंक का है।
• प्रश्न संख्या 9 से 11 तक प्रत्येक 3 अंक का है।

प्रश्न 1: 645 और 876 का अनुमानित योग क्या है? (1 अंक) (a) 1300 (b) 1400 (c) 1500 (d) 1600

उत्तर: (c) समाधान: चूंकि, 645 600 के करीब है, और 876 900 के करीब है। इस प्रकार, अनुमानित योग = 600 + 900 = 1500।

प्रश्न 2: 812 – 493 का अनुमानित अंतर क्या है? (1 अंक) (a) 200 (b) 250 (c) 300 (d) 350

उत्तर: (c) समाधान: 812 – 493 चूंकि, 812 800 के करीब है, और 493 500 के करीब है। इस प्रकार, अनुमानित अंतर = 800 – 500 = 300।

प्रश्न 3: निम्नलिखित में से कौन सा संख्या समूह 24,539 के बराबर है? (1 अंक) (a) 5-अंक संख्या = 21,000, 3-अंक संख्या = 539 (b) 5-अंक संख्या = 20,000, 3-अंक संख्या = 439 (c) 5-अंक संख्या = 24,000, 3-अंक संख्या = 539 (d) 5-अंक संख्या = 19,000, 3-अंक संख्या = 539

उत्तर: (c) समाधान: 24,000 + 539 = 24,539।

प्रश्न 4: निम्नलिखित में से कौन सी 3-अंक की पलिंड्रोम संख्या है जो 1, 2, और 3 अंकों का उपयोग करके बनाई जा सकती है? (1 अंक) (a) 111 (b) 122 (c) 123 (d) 132

उत्तर: (a) समाधान: 3-अंक की पलिंड्रोम वह संख्या है जो आगे और पीछे समान पढ़ी जाती है। 111 एक पलिंड्रोम है, जबकि अन्य नहीं हैं।

प्रश्न 5: निम्नलिखित में से कौन सी संख्या के अंकों का योग 14 है? (1 अंक) (a) 59 (b) 67 (c) 85 (d) 92

उत्तर: (क) समाधान: 59 के अंकों का योग 5 + 9 = 14 है।

प्रश्न 6: उन 3-अंकीय संख्याओं के अंकों का योग निकालें जिनके अंक अनुक्रमिक हैं (जैसे, 123, 234)। क्या आपको कोई पैटर्न दिखाई देता है? क्या यह पैटर्न जारी रहेगा? (2 अंक)

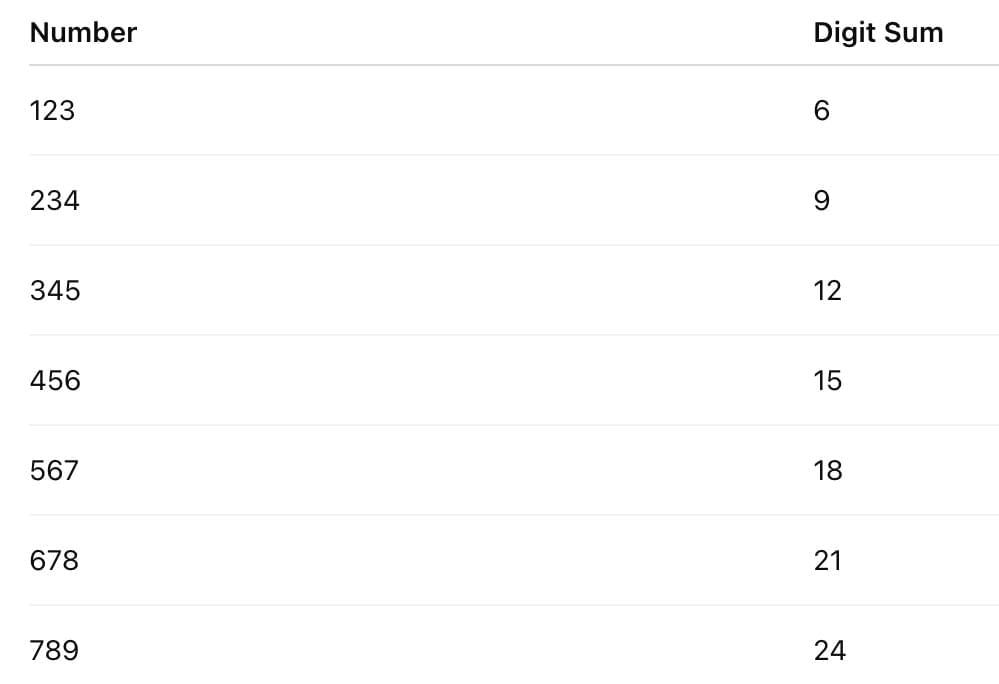
अंक का योग हर बार 3 से बढ़ता है। हाँ, पैटर्न जारी रहता है क्योंकि अंकों में क्रमिक प्रगति होती है।

प्रश्न 7: अब समय 02:15 है। घड़ी में अगली पलिंड्रोमिक समय दिखाने के लिए कितने मिनट बाकी हैं? उसके बाद का समय क्या है? (2 अंक)

उत्तर: अब समय – 02:15। अब, अगला पलिंड्रोमिक समय 02:20 है। इसलिए, 02:20 – 02:15 = 5 मिनट। इसके बाद अगला समय 03:30 है। इसलिए, 03:30 – 02:20 = 70 मिनट।

प्रश्न 8: हम 40,000 और 80,000 के बीच के 5-अंकीय संख्याओं का समूह हैं जिसमें हमारे सभी अंक सम हैं। हमारे समूह में सबसे बड़ा संख्या कौन है? हमारे समूह में सबसे छोटा संख्या कौन है? हम में से कौन 60,000 के सबसे निकट है? (2 अंक)

उत्तर:

• अनुमति प्राप्त सम अंकों में हैं: 0, 2, 4, 6, 8। चूंकि संख्या 40,000 और 80,000 के बीच होनी चाहिए, पहले अंक (दस हजार स्थान) या तो 4 या 6 होना चाहिए (यह सम होना चाहिए)।

सबसे छोटी संख्या: 4 के बाद सबसे छोटे सम अंकों का चयन करें → 40000

सबसे बड़ी संख्या: 6 से शुरू होने वाले सबसे बड़े सम अंकों का चयन करें → 68888

60000 के निकटतम: 60000 के निकटतम संख्या बनाने के लिए सम अंकों का चयन करें → 60000

उत्तर:

• सबसे छोटी संख्या: 40000
• सबसे बड़ी संख्या: 68888
• 60000 के निकटतम: 60000

प्रश्न 9: सबसे छोटी और सबसे बड़ी 5-अंकीय पलिंड्रोम का योग क्या है? उनका अंतर क्या है? (3 अंक)

उत्तर:

• सबसे छोटा 5-अंकों का पलिंड्रोम = 10001
• सबसे बड़ा 5-अंकों का पलिंड्रोम = 99999

योग:

अंतर:

अंतिम उत्तर:

• योग = 110000
• अंतर = 89998

प्रश्न 10. अंक योग 18. (3 अंक) (क) अन्य संख्याएँ लिखें जिनके अंकों का योग 18 है। (ख) सबसे छोटी संख्या क्या है जिसका अंक योग 18 है? (ग) सबसे बड़ी 5-अंकों की संख्या क्या है जिसका अंक योग 18 है? (घ) आप 18 अंक योग वाली कितनी बड़ी संख्या बना सकते हैं? क्या आप और भी बड़ी संख्या बना सकते हैं?

उत्तर: (क) समाधान: कुछ संख्याएँ जिनके अंकों का योग 18 है: 99, 189, 288, 297, 369, 459, 567, 678, 777, 885, 993, 1098, 1187, 1276। (ख) सबसे छोटी संख्या जिसका अंक योग 18 = 99। (ग) अंक योग 18 वाली सबसे बड़ी 5-अंकों की संख्या 99000 है (9 9 0 0 0 = 18)। (घ) हाँ, आप 18 अंक योग वाली बहुत बड़ी संख्याएँ बना सकते हैं, जैसे कि 18 का योग देने वाले अंकों के बाद और अंकों (शून्य) को जोड़कर। उदाहरण के लिए:

• 9900000000 (अंक योग फिर भी 18)
• 900000009 (9 0 0 0 0 0 0 0 9 = 18) इस प्रकार, आप 18 अंक योग वाली और भी बड़ी संख्याएँ बना सकते हैं, अंकों की संख्या बढ़ाकर।

900000009 (9 0 0 0 0 0 0 0 9 = 18) इस प्रकार, आप 18 अंक योग वाली और भी बड़ी संख्याएँ बना सकते हैं, अंकों की संख्या बढ़ाकर।

प्रश्न 11. क्या 2-अंकों की संख्या से शुरू करके संख्याओं को उलटकर और जोड़ते रहने पर हमेशा एक पलिंड्रोम मिलेगा? (3 अंक)

उत्तर:

हम उदाहरणों के साथ परीक्षण करते हैं:

• उदाहरण 1: 23 → उलट = 32 → 23 + 32 = 55 → पलिंड्रोम
• उदाहरण 2: 56 → उलट = 65 → 56 + 65 = 121 → पलिंड्रोम
• लेकिन हमेशा सुनिश्चित नहीं: उदाहरण: 196 → 196 + 691 = 887 → 887 + 788 = 1675 → और इसी प्रकार… (जाने पहचाने चरणों में कभी पलिंड्रोम नहीं बनता)

उदाहरण 1: 23 → उलट = 32 → 23 + 32 = 55 → पलिंड्रोम

उदाहरण 2: 56 → उल्टा = 65 → 56 65 = 121 → पैलिंड्रोम

• उदाहरण 2: 56 → उल्टा = 65 → 56 65 = 121 → पैलिंड्रोम

लेकिन हमेशा यह सुनिश्चित नहीं होता: उदाहरण: 196 → 196 691 = 887 → 887 788 = 1675 → और इसी तरह… (कभी भी ज्ञात चरणों में पैलिंड्रोम नहीं बनता)

• लेकिन हमेशा यह सुनिश्चित नहीं होता: उदाहरण: 196 → 196 691 = 887 → 887 788 = 1675 → और इसी तरह… (कभी भी ज्ञात चरणों में पैलिंड्रोम नहीं बनता)

निष्कर्ष: अधिकांश 2-अंक संख्या अंततः उलटने की जोड़ से पैलिंड्रोम बन जाती हैं, लेकिन कुछ संख्या (जैसे 196) शायद ऐसा कभी न करें।