Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > NCERT Solutions: संख्या खेल

संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

पृष्ठ 55

प्रश्न 1: विभिन्न परिस्थितियों के बारे में सोचें जहाँ हम संख्याओं का उपयोग करते हैं। ऐसी पाँच विभिन्न परिस्थितियों की सूची बनाएं जिनमें संख्याओं का उपयोग किया जाता है। देखें कि आपके सहपाठियों ने क्या सूचीबद्ध किया है, साझा करें और चर्चा करें। उत्तर: संख्याओं का उपयोग करने वाली पाँच विभिन्न परिस्थितियाँ:

समय बताने के लिए, हम घड़ी पर घंटे और मिनट देखने के लिए संख्याओं का उपयोग करते हैं।
जब हम खरीदारी करते हैं, तो हम वस्तुओं की कीमतें देखने और कुल लागत की गणना करने के लिए संख्याओं का उपयोग करते हैं।
खेलों में, स्कोर रखने के लिए संख्याओं का उपयोग किया जाता है, जैसे फुटबॉल में गोल या क्रिकेट में रन।
ऊँचाई या वजन मापने के दौरान, संख्याएँ यह बताती हैं कि कोई कितना लंबा या भारी है।
विद्यालय में, संख्याएँ परीक्षाओं या असाइनमेंट में अंक के लिए उपयोग की जाती हैं।

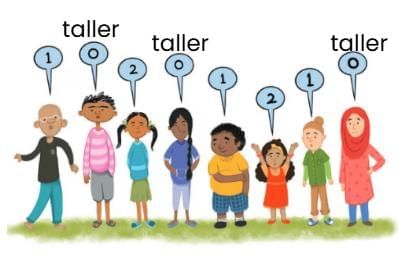
प्रश्न 2: कुछ बच्चे पार्क में एक पंक्ति में खड़े हैं। प्रत्येक बच्चा एक संख्या कहता है। एक बच्चा '1' कहता है अगर उसके पास एक ही ऊँचा बच्चा खड़ा है। एक बच्चा '2' कहता है अगर उसके पास दोनों पड़ोसी बच्चे ऊँचे हैं। एक बच्चा '0' कहता है, अगर उसके पास कोई भी पड़ोसी बच्चा ऊँचा नहीं है। अर्थात्, प्रत्येक व्यक्ति अपने पास के ऊँचे पड़ोसियों की संख्या बताता है।

संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

आपको क्या लगता है कि ये संख्याएँ क्या दर्शाती हैं? उत्तर: ये संख्याएँ उस बच्चे के पास के ऊँचे बच्चों की संख्या को दर्शाती हैं।

पृष्ठ 56

नीचे दिए गए प्रश्नों के उत्तर देने का प्रयास करें और अपनी तर्कशीलता साझा करें:

प्रश्न 1: क्या बच्चे अपने आप को इस तरह से व्यवस्थित कर सकते हैं कि जो बच्चे पंक्ति के अंत में हैं वे '2' कहें? उत्तर: हाँ, बच्चे अपने आप को इस तरह से व्यवस्थित कर सकते हैं कि पंक्ति के अंत में खड़े बच्चे '2' कहें क्योंकि, जैसा कि ऊपर दिए गए पैराग्राफ में उल्लेख किया गया है, एक बच्चा '2' कहता है यदि उसके पास खड़े दोनों बच्चे ऊँचे हैं।

प्रश्न 2: क्या हम बच्चों को एक लाइन में इस तरह व्यवस्थित कर सकते हैं कि सभी केवल 0 कहें? उत्तर: हाँ, बच्चों को इस तरह व्यवस्थित करना संभव है कि सभी केवल 0 कहें। क्योंकि, अनुच्छेद में दिया गया वाक्य कहता है, 'एक बच्चा '0' कहता है, यदि उसके पास खड़े बच्चों में से कोई भी ऊँचा नहीं है। अर्थात्, प्रत्येक व्यक्ति अपने पास के ऊँचे पड़ोसियों की संख्या कहता है।

प्रश्न 3: क्या दो बच्चे जो एक-दूसरे के पास खड़े हैं, वही संख्या कह सकते हैं? उत्तर: हाँ, दो बच्चे जो एक-दूसरे के पास खड़े हैं, वही संख्या कह सकते हैं यदि उन्हें उनकी ऊँचाई के क्रम में बढ़ती या घटती स्थिति में व्यवस्थित किया जाए।

प्रश्न 4: एक समूह में 5 बच्चे हैं, जिनकी ऊँचाई अलग-अलग है। क्या वे इस तरह खड़े हो सकते हैं कि चार '1' कहें और आखिरी बच्चा '0' कहे? क्यों या क्यों नहीं? उत्तर: हाँ, यह केवल तभी संभव है जब 5 बच्चों को उनकी ऊँचाई के क्रम में बढ़ते हुए व्यवस्थित किया जाए।

प्रश्न 5: क्या इस समूह में 5 बच्चों के लिए क्रम 1, 1, 1, 1, 1 संभव है? उत्तर: नहीं, क्रम 1, 1, 1, 1, 1 संभव नहीं है क्योंकि केवल पाँच बच्चे हैं और कम से कम एक बच्चे के पास कोई ऊँचा पड़ोसी नहीं होना चाहिए, जिसका अर्थ है कि वह '0' कहेगा। यह असंभव है कि हर बच्चे के पास एक ऊँचा पड़ोसी हो।

प्रश्न 6: क्या क्रम 0, 1, 2, 1, 0 संभव है? क्यों या क्यों नहीं? उत्तर: हाँ, यह संभव है यदि सबसे छोटे बच्चे को बीच में रखा जाए, और ऊँचाई केंद्र से बाहर की ओर बढ़ते समय सममित रूप से बढ़े।

प्रश्न 7: आप इन पाँच बच्चों को इस तरह कैसे पुनर्व्यवस्थित करेंगे कि अधिकतम संख्या में बच्चे ‘2’ कहें? उत्तर: हाँ, यह संभव है यदि ऊँचे और छोटे बच्चे बारी-बारी से व्यवस्थित हों।

पृष्ठ 57 और 58

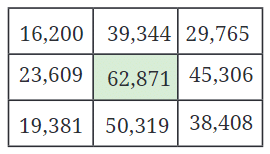
प्रश्न 1: नीचे दिए गए तालिका में सुपरसेल का रंग या चिह्नित करें।

उत्तर:

प्रश्न 2: नीचे दिए गए तालिका में केवल 4-अंकों की संख्याएँ भरें ताकि सुपरसेल ठीक वही रंगीन कोशिकाएँ हों।

उत्तर:

प्रश्न 3: नीचे दिए गए तालिका में भरें ताकि हम अधिकतम संभव सुपरसेल प्राप्त कर सकें। संख्या 100 और 1000 के बीच हो और पुनरावृत्ति न हो।

उत्तर:

प्रश्न 4: ऊपर दिए गए तालिका में 9 संख्याओं में से कितने सुपरसेल हैं?

उत्तर: 9 संख्याओं में से, ऊपर दिए गए तालिका में 5 सुपरसेल हैं।

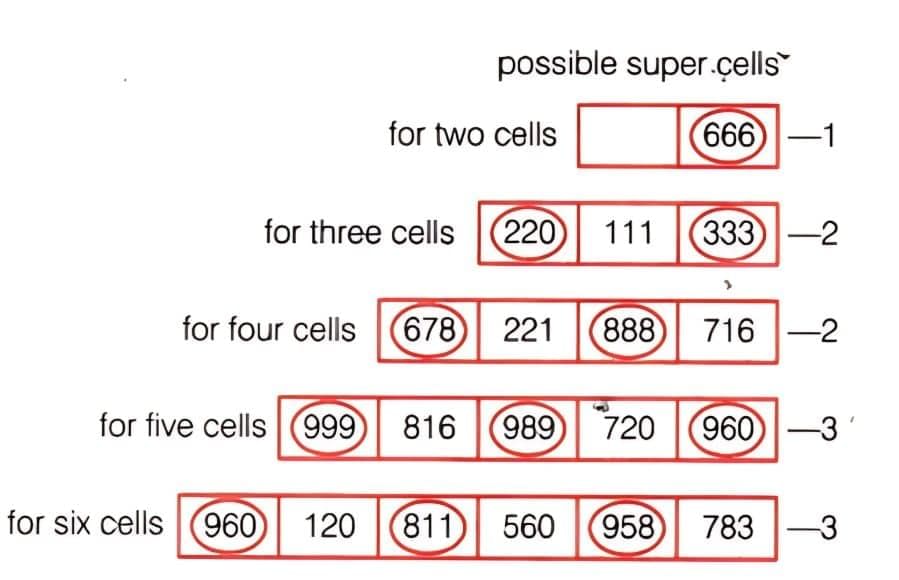
प्रश्न 5: विभिन्न कोशिकाओं की संख्याओं के लिए संभव सुपरसेल की संख्या ज्ञात करें। क्या आप कोई पैटर्न देखते हैं? अधिकतम सुपरसेल प्राप्त करने के लिए तालिका को भरने की विधि क्या है? अपनी रणनीति साझा करें।

उत्तर: यदि n विषम कोशिकाएँ हैं तो सुपरसेल की संख्या = n। यदि n सम कोशिकाएँ हैं तो सुपरसेल की संख्या = n/2

प्रश्न 6: क्या आप बिना संख्याओं को दोहराए एक सुपरसेल तालिका भर सकते हैं ताकि कोई सुपरसेल न हो? क्यों या क्यों नहीं?

उत्तर: नहीं, बिना संख्याओं को दोहराए सुपरसेल तालिका भरना संभव नहीं है ताकि कोई सुपरसेल न हो। इसके दो मामले हैं:

मामला I: यदि हम कोशिकाओं को अवरोही क्रम में भरते हैं, तो पहली कोशिका सुपरसेल होगी।
मामला II: यदि हम कोशिकाओं को आरोही क्रम में भरते हैं, तो अंतिम कोशिका सुपरसेल होगी।

यदि हम किसी क्रम का पालन नहीं करते हैं, तो निश्चित रूप से कम से कम एक सुपरसेल होगा।

प्रश्न 7: क्या तालिका में सबसे बड़ी संख्या वाली कोशिका हमेशा एक सुपरसेल होगी? क्या तालिका में सबसे छोटी संख्या वाली कोशिका एक सुपरसेल हो सकती है? क्यों या क्यों नहीं?

उत्तर: हाँ, तालिका में सबसे बड़ी संख्या वाली कोशिका हमेशा एक सुपरसेल होगी। चूंकि सबसे बड़ी संख्या तालिका में किसी अन्य संख्या से बड़ी होती है, यह स्वाभाविक रूप से अपनी आस-पास की संख्याओं से भी बड़ी होगी। इसलिए, यह हमेशा एक सुपरसेल होगी। नहीं, तालिका में सबसे छोटी संख्या वाली कोशिका एक सुपरसेल नहीं हो सकती। चूंकि तालिका में सबसे छोटी संख्या सभी अन्य संख्याओं से कम या उसके बराबर होती है, यह अपनी आस-पास की संख्याओं से बड़ी नहीं हो सकती। इसलिए, यह एक सुपरसेल नहीं हो सकती।

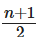
Q8: एक तालिका भरें ऐसी कि जिस सेल में दूसरा सबसे बड़ा नंबर हो, वह एक सुपरसेल न हो। उत्तर: सबसे बड़ा नंबर = 850 दूसरा सबसे बड़ा नंबर = 730

Q9: एक तालिका भरें ऐसी कि जिस सेल में दूसरा सबसे बड़ा नंबर हो, वह एक सुपरसेल न हो, लेकिन दूसरा सबसे छोटा नंबर एक सुपरसेल हो। क्या यह संभव है? उत्तर: हाँ, यह संभव है। यहाँ एक संभावित व्यवस्था है: सबसे बड़ा नंबर = 750 दूसरा सबसे बड़ा नंबर = 640 सबसे छोटा नंबर = 100 दूसरा सबसे छोटा नंबर = 210

Q10: इस पहेली के अन्य विविधताएँ बनाएं और अपने सहपाठियों को चुनौती दें। उत्तर: एक तालिका भरें ऐसी कि केवल सम संख्याएँ सुपरसेल हों। एक तालिका भरें ऐसी कि सभी सुपरसेल 5 द्वारा विभाज्य हों।

तालिका 2 को 5-अंक के नंबरों से पूरा करें जिनके अंक ‘1’, ‘0’, ‘6’, ‘3’, और ‘9’ किसी क्रम में हैं। केवल एक रंगीन सेल में ऐसा नंबर होना चाहिए जो अपने सभी पड़ोसियों से बड़ा हो।

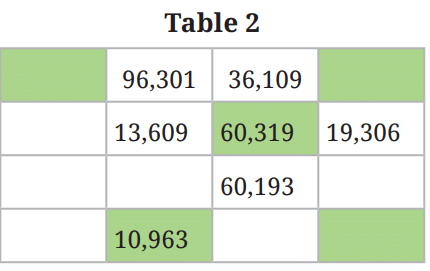
तालिका में सबसे बड़ा नंबर ____________ है। तालिका में सबसे छोटी सम संख्या ____________ है। तालिका में 50,000 से बड़ी सबसे छोटी संख्या ____________ है। एक बार जब आप ऊपर की तालिका भर लें, तो हजारों अंक के बाद उपयुक्त रूप से अल्पविराम लगाएं।

उत्तर:

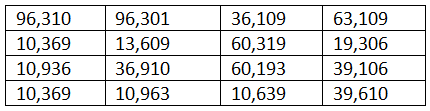
तालिका में सबसे बड़ा नंबर 96,310 है।
तालिका में सबसे छोटी सम संख्या 10,936 है।
तालिका में 50,000 से बड़ी सबसे छोटी संख्या 60,193 है।

पृष्ठ 59

समझें

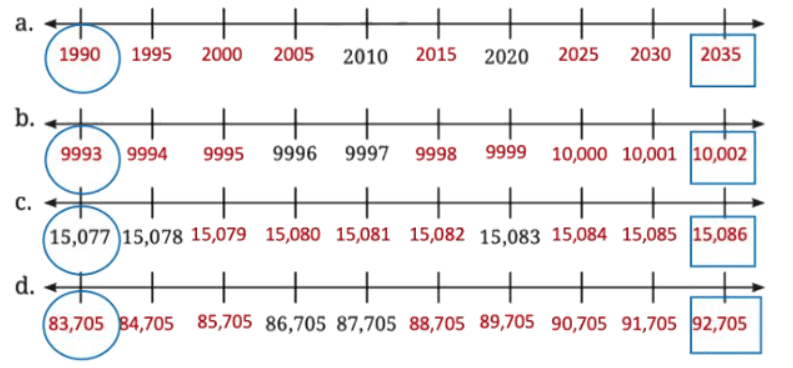
Q1: नीचे दिए गए नंबर लाइनों पर चिह्नित संख्याओं की पहचान करें, और शेष स्थानों को लेबल करें। प्रत्येक अनुक्रम में सबसे छोटी संख्या के चारों ओर एक वृत्त बनाएँ और सबसे बड़ी संख्या के चारों ओर एक बॉक्स बनाएँ। उत्तर:

पृष्ठ 60

प्रश्न 1: पता करें कि कितने संख्याएँ हैं जिनमें दो अंक, तीन अंक, चार अंक और पाँच अंक हैं।

प्रश्न 2: अंक योग 14

(क) अन्य संख्याएँ लिखें जिनके अंकों का योग 14 हो।
(ख) सबसे छोटी संख्या कौन-सी है जिसका अंक योग 14 है?
(ग) सबसे बड़ी 5-अंक की संख्या क्या है जिसका अंक योग 14 है?
(घ) आप कितनी बड़ी संख्या बना सकते हैं जिसका अंक योग 14 हो? क्या आप और भी बड़ी संख्या बना सकते हैं?

उत्तर:

(क) कुछ संख्याएँ जिनके अंकों का योग 14 है: 59, 68, 77, 86, 95, 149, 158, 167, 176, 185, 194, 239, 248, 257, 266, 275, 281, 293
(ख) सबसे छोटी संख्या जिसका अंक योग 14 है = 59।
(ग) सबसे बड़ी 5-अंक की संख्या जिसमें 0 हो और जिसका अंक योग 14 = 95,000। 0 के बिना सबसे बड़ी 5-अंक की संख्या जिसका अंक योग 14 = 92,111।
(घ) अनंत संख्याएँ बनाई जा सकती हैं जिनका अंक योग 14 है। हाँ, हम एक और बड़ी संख्या बना सकते हैं।

प्रश्न 3: 40 से 70 तक की सभी संख्याओं के अंक योग ज्ञात करें। अपनी अवलोकन कक्षा के साथ साझा करें।

उत्तर:

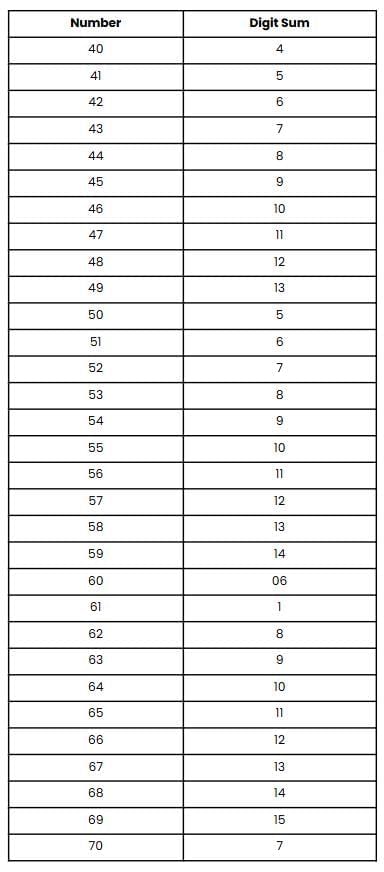
अवलोकन:

40 से 49 तक: अंक योग 4 से 13 तक बढ़ा
50 से 59 तक: अंक योग 5 से 14 तक बढ़ा
60 से 69 तक: अंक योग 6 से 15 तक बढ़ा
70 से 79 तक: अंक योग 7 से 16 तक बढ़ेगा

प्रश्न 4: उन 3-अंक की संख्याओं का अंक योग ज्ञात करें जिनके अंक क्रम में हैं (उदाहरण के लिए, 345)। क्या आप एक पैटर्न देखते हैं? क्या यह पैटर्न जारी रहेगा?

उत्तर:

1 2 3 = 6,

2 3 4 = 9,

3 4 5 = 12,

4 5 6 = 15,

5 6 7 = 18,

6 7 8 = 21,

7 8 9 = 24।

हाँ, पैटर्न 3 का एक तालिका है जो 3 × 2 से 3 × 8 तक है।

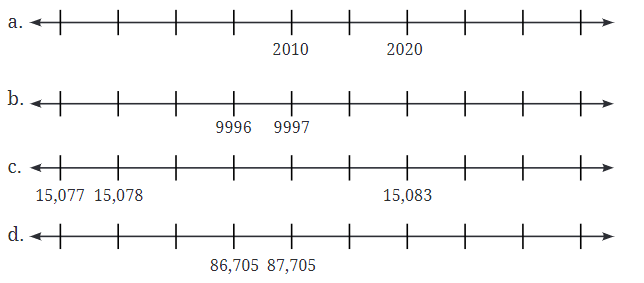
हम इस पैटर्न को 789 के बाद जारी नहीं रख सकते।

पृष्ठ 61

प्रश्न 1: संख्याओं 1-100 में, अंक '7' कितनी बार आएगा? उत्तर: हमें '7' की कुल संख्या 20 मिलती है।

प्रश्न 2: संख्याओं 1-1000 में, अंक '7' कितनी बार आएगा? उत्तर: संख्याओं 1 से 1000 तक की सूची में '7' 300 बार लिखा जाएगा।

प्रश्न 3: इन अंकों का उपयोग करके सभी संभावित 3-आंकड़े वाले पलिंड्रोम लिखिए। उत्तर:

पृष्ठ 62

प्रश्न 1: क्या 2-आंकड़े वाली संख्या से शुरू होकर बार-बार संख्याओं को उलटने और जोड़ने से हमेशा पलिंड्रोम मिलेगा? अन्वेषण करें और पता करें। उत्तर: सभी दो-आंकड़े वाली संख्याएँ अंततः पलिंड्रोम बन जाती हैं जब उन्हें बार-बार उलटा और जोड़ा जाता है। 10,000 के तहत लगभग 80% सभी संख्याएँ चार या कम कदमों में पलिंड्रोम में बदल जाती हैं; उन में से लगभग 90% सात कदमों या कम में बदल जाती हैं। उदाहरण 1: संख्या 12 1. प्रारंभिक संख्या: 12 2. उलटें: 21 3. जोड़ें: 12 + 21 = 33 4. पलिंड्रोम जांचें: 33 एक पलिंड्रोम है। • परिणाम: 33 एक पलिंड्रोम है। उदाहरण 2: संख्या 89 1. प्रारंभिक संख्या: 89 2. उलटें: 98 3. जोड़ें: 89 + 98 = 187 4. पलिंड्रोम जांचें: 187 एक पलिंड्रोम नहीं है। 5. 187 को उलटें: 781 6. जोड़ें: 187 + 781 = 968 7. पलिंड्रोम जांचें: 968 एक पलिंड्रोम नहीं है।

पहेली का समय

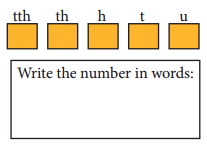
मैं एक 5-आंकड़े का पलिंड्रोम हूँ। मैं एक विषम संख्या हूँ। मेरा 't' अंक मेरे 'u' अंक का दो गुना है। मेरा 'h' अंक मेरे 't' अंक का दो गुना है। मैं कौन हूँ? ___________ उत्तर: 12421

पृष्ठ 63

अलग-अलग 4-आंकड़े की संख्याएँ लें और इन चरणों को आजमाएँ। पता करें कि क्या होता है। उत्तर: चयनित 4-आंकड़े की संख्या 1234

शुरुआती संख्या: 1234

उल्टी क्रम: 4321
सिद्धांत क्रम: 1234
घटाना: 4321 – 1234 = 3087

दोहराएं:

3087 का उल्टी क्रम: 8730
3087 का सिद्धांत क्रम: 0378
घटाना: 8730 – 0378 = 8352

8352 का उल्टी क्रम: 8532
8352 का सिद्धांत क्रम: 2358
घटाना: 8532 – 2358 = 6174

परिणाम: 6174 (कपरेकर स्थिरांक)

इन ही चरणों को कुछ 3-अंक संख्या के साथ दोहराएं। कौन सी संख्या शुरू में दोहराएगी? उत्तर: हम इसे दो उदाहरणों की मदद से करेंगे:

1. संख्या 123

शुरुआती संख्या: 123
उल्टी क्रम: 321
सिद्धांत क्रम: 123
घटाना: 321 – 123 = 198

198 का उल्टी क्रम: 981
198 का सिद्धांत क्रम: 189
घटाना: 981 – 189 = 792

792 का उल्टी क्रम: 972
792 का सिद्धांत क्रम: 279
घटाना: 972 – 279 = 693

693 का उल्टी क्रम: 963
693 का सिद्धांत क्रम: 369
घटाना: 963 – 369 = 594

594 का उल्टी क्रम: 954
594 का सिद्धांत क्रम: 459
घटाना: 954 – 459 = 495

495 का उल्टी क्रम: 954
495 का सिद्धांत क्रम: 459
घटाना: 954 – 459 = 495

परिणाम: संख्या 495 दोहराना शुरू करती है।

2. अब संख्या 317 लेते हैं

शुरुआती संख्या: 317
उल्टी क्रम: 731
सिद्धांत क्रम: 137
घटाना: 731 – 137 = 594

परिणाम: संख्या 495 दोहराना शुरू करती है। जब कपरेकर की प्रक्रिया को 3-अंक संख्याओं पर लागू किया जाता है, तो संख्या 495 अक्सर प्राप्त होती है और दोहराना शुरू करती है। यह संख्या 3-अंक संख्याओं के लिए कपरेकर स्थिरांक के रूप में जानी जाती है।

पृष्ठ 64 और 65

इन प्रकारों में से प्रत्येक के लिए 12-घंटे की घड़ी पर सभी संभावित समय खोजने का प्रयास करें। उदाहरण के लिए, 4:44, 10:10, 12:21। उत्तर: 01:10, 02:20, 03:30, 04:40, 05:50, 10:01, 11:11, 12:21

कुछ अन्य तिथियाँ खोजें जो इस रूप में हैं, जैसे 20/12/2012, जहाँ अंक '2', '0', '1', और '2' इस क्रम में दोहराए जाते हैं। उत्तर: 11/02/2011, 22/02/2022, 01/10/2010, 10/01/2010, 02/02/2020

1. प्रतिभा अंक '4', '7', '3' और '2' का उपयोग करती है, और इनके साथ सबसे छोटे और बड़े 4-अंक के नंबर बनाती है: 2347 और 7432। इन दोनों संख्याओं के बीच का अंतर है 7432 - 2347 = 5085। इन दोनों संख्याओं का योग 9779 है। 4-अंक की संख्याएँ चुनें ताकि:

(क) सबसे बड़ी और छोटी संख्याओं के बीच का अंतर 5085 से अधिक हो।
(ख) सबसे बड़ी और छोटी संख्याओं के बीच का अंतर 5085 से कम हो।
(ग) सबसे बड़ी और छोटी संख्याओं का योग 9779 से अधिक हो।
(घ) सबसे बड़ी और छोटी संख्याओं का योग 9779 से कम हो। उत्तर:
- (क) अंक: 9, 6, 5, 3 सबसे बड़ी संख्या = 9653 सबसे छोटी संख्या = 3569 अंतर = 9653 - 3569 = 6084।
- (ख) अंक: 4, 6, 3, 2 सबसे बड़ी 4-अंक की संख्या: 6432 सबसे छोटी 4- अंक की संख्या = 2346 अंतर: 6432 – 2346 = 4086 < 5085="" />
- (ग) अंक: 9, 8, 7, 1 सबसे बड़ी संख्या = 9871 सबसे छोटी संख्या = 1789 योग = 9871 + 1789 = 11660
- (घ) अंक: 8, 5, 2, 1 सबसे बड़ी संख्या = 8321 सबसे छोटी संख्या = 1238 योग = 8321 + 1238 = 9559
  प्रश्न 2: सबसे छोटे और सबसे बड़े 5-अंक के पलिंड्रोम का योग क्या है? उनका अंतर क्या है? उत्तर: सबसे छोटा 5-अंक का पलिंड्रोम = 10001 सबसे बड़ा 5-अंक का पलिंड्रोम = 99999 योग = 10001 + 99999 = 110000 अंतर = 99999 - 10001 = 89998
  
  प्रश्न 3: अब समय 10:01 है। घड़ी अगली पलिंड्रोम समय दिखाने में कितने मिनट लगेंगे? उसके बाद का समय क्या होगा? उत्तर: प्रमुख समय = 10:01 10:01 के बाद अगला पलिंड्रोम समय = 11:11 अंतर = 11:11 - 10:01 = 70 मिनट। इस प्रकार, अगला पलिंड्रोम समय 70 मिनट बाद दिखता है। 11:11 के बाद अगला पलिंड्रोम समय = 12:21 अंतर = 12:21 – 11:11 = 70 मिनट = 1 घंटा 10 मिनट। इस प्रकार, अगला पलिंड्रोम समय 1 घंटे 10 मिनट बाद दिखता है और अगला 12:21 है, जो कुल 2 घंटे 20 मिनट बाद आता है।
  प्रश्न 4: संख्या 5683 को कपरेकर स्थिरांक तक पहुँचने में कितने राउंड लगते हैं? उत्तर: दी गई संख्या 5683 है।
  - 1st राउंड: सबसे बड़ी संख्या = 8653, सबसे छोटी संख्या = 3568, घटाव = 8653 - 3568 = 5085
  - 2nd राउंड: सबसे बड़ी संख्या = 8550, सबसे छोटी संख्या = 0558, घटाव = 8550 - 0558 = 7992
  - 3rd राउंड: सबसे बड़ी संख्या = 9972, सबसे छोटी संख्या = 2799, घटाव = 9972 - 2799 = 7173
  - 4th राउंड: सबसे बड़ी संख्या = 7731, सबसे छोटी संख्या = 1377, घटाव = 7731 - 1377 = 6354
  - 5th राउंड: सबसे बड़ी संख्या = 6543, सबसे छोटी संख्या = 3456, घटाव = 6543 - 3456 = 3087
  - 6th राउंड: सबसे बड़ी संख्या = 8730, सबसे छोटी संख्या = 0378, अंतर = 8730 - 0378 = 8352
  - 7th राउंड: सबसे बड़ी संख्या = 8532, सबसे छोटी संख्या = 2358, अंतर = 8532 - 2358 = 6174 इसलिए, संख्या 5683 को 6174 तक पहुँचने में 7 राउंड लगते हैं, जो कपरेकर स्थिरांक है।

पृष्ठ 66 और 67

प्रश्न 1: नीचे दिए गए प्रत्येक परिदृश्य के लिए उदाहरण लिखें जहाँ संभव हो। क्या आप सभी मामलों के लिए उदाहरण खोज सकते हैं? यदि नहीं, तो सोचें और चर्चा करें कि ऐसा क्यों हो सकता है। अन्य ऐसे प्रश्न बनाएं और अपने सहपाठियों को चुनौती दें। उत्तर:

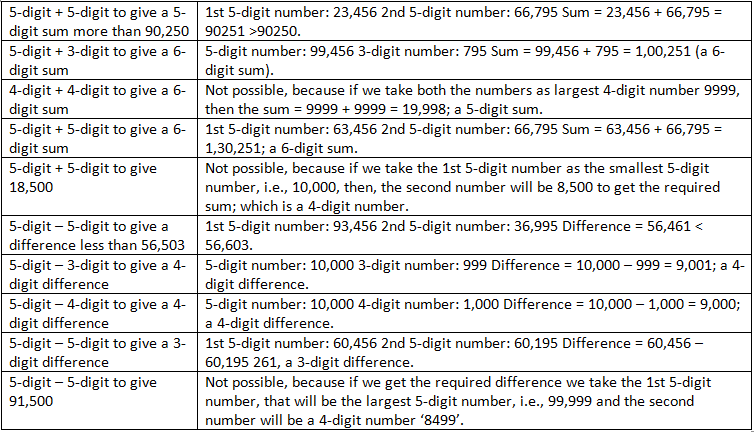
प्रश्न 2: हमेशा, कभी-कभी, कभी नहीं? नीचे कुछ कथन दिए गए हैं। सोचें, खोजें और पता करें कि क्या प्रत्येक कथन 'हमेशा सत्य', 'केवल कभी-कभी सत्य' या 'कभी नहीं सत्य' है। आप ऐसा क्यों सोचते हैं? अपने तर्क लिखें; इस पर कक्षा में चर्चा करें। (क) 5-अंक संख्या 5-अंक संख्या 5-अंक संख्या देती है (ख) 4-अंक संख्या 2-अंक संख्या 4-अंक संख्या देती है (ग) 4-अंक संख्या 2-अंक संख्या 6-अंक संख्या देती है (घ) 5-अंक संख्या - 5-अंक संख्या 5-अंक संख्या देती है (ड) 5-अंक संख्या - 2-अंक संख्या 3-अंक संख्या देती है। उत्तर: (क) केवल कभी-कभी सत्य। दिया गया कथन है '5-अंक संख्या 5-अंक संख्या 5-अंक संख्या देती है'। यह केवल कभी-कभी सत्य है। उदाहरण: 10000 + 10000 = 20000 अर्थात् 5-अंक संख्या और 99999 + 99999 = 199998 अर्थात् 6-अंक संख्या।

(ख) दिया गया कथन है '4-अंक संख्या 2-अंक संख्या 4-अंक संख्या देती है'। यह केवल कभी-कभी सत्य है। उदाहरण: 1000 + 10 = 1010 अर्थात् 4-अंक संख्या और 9999 + 10 = 10009 अर्थात् 5-अंक संख्या।

(ग) दिया गया कथन है '4-अंक संख्या 2-अंक संख्या 6-अंक संख्या देती है'। यह कभी नहीं सत्य है। उदाहरण: 9999 + 99 = 10098 अर्थात् 5-अंक संख्या।

(घ) दिया गया कथन है '5-अंक संख्या - 5-अंक संख्या 5-अंक संख्या देती है'। यह केवल कभी-कभी सत्य है। उदाहरण: 99999 - 10000 = 89999 अर्थात् 5-अंक संख्या और 98765 - 94321 = 4444 अर्थात् 4-अंक संख्या।

(e) दिया गया कथन है '5-अंकों वाला संख्या – 2-अंकों वाली संख्या से 3-अंकों वाली संख्या मिलती है'। यह कभी सच नहीं होता, जैसे 10000 – 99 = 9901 अर्थात यह 4-अंकों वाली संख्या है।

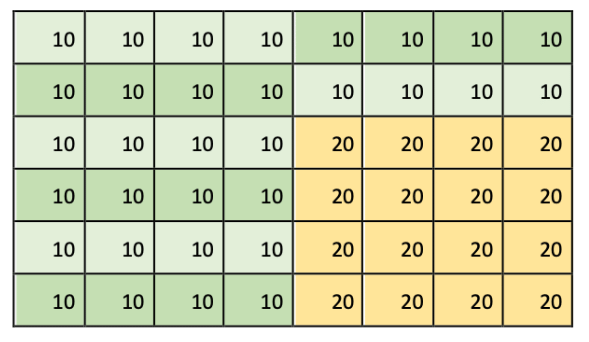
Q3: नीचे दिए गए आकृतियों में संख्याओं का योग ज्ञात करें। क्या हमें उन्हें एक-एक करके जोड़ना चाहिए या किसी तेज़ तरीके का उपयोग कर सकते हैं? कक्षा में यह चर्चा करें कि आपने इन प्रश्नों को हल करने के लिए कौन से विभिन्न तरीके अपनाए।

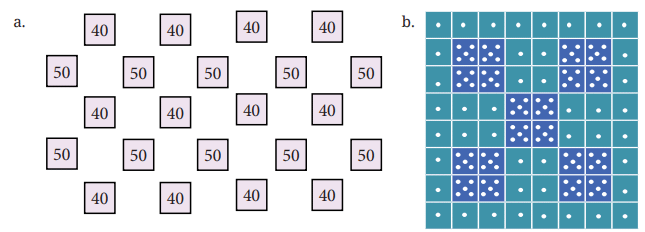
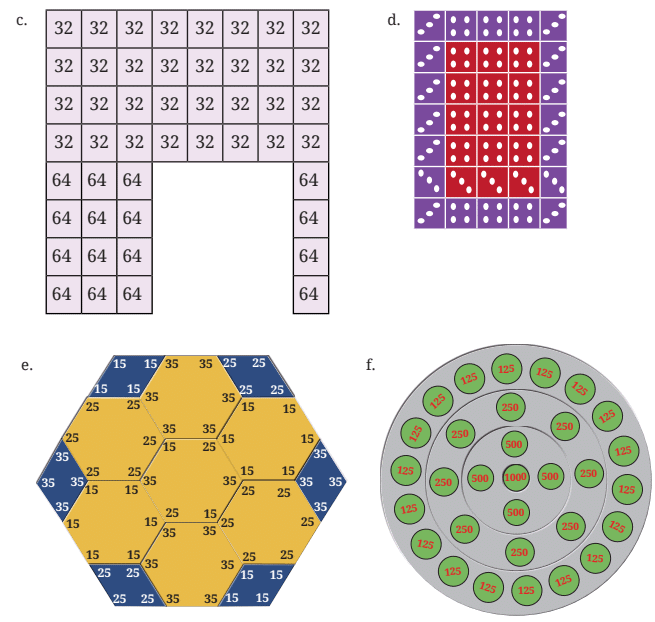
उत्तर: (a) आकृति (a) में, संख्या 40 12 बार दोहराई गई है और संख्या 50 10 बार दोहराई गई है। अतः सभी संख्याओं का योग = 40 × 12 + 50 × 10 = 480 + 500 = 980।

(b) आकृति (b) में, 1 बिंदु (•) 44 बार है और 5 बिंदु (•) 20 बार हैं। अतः सभी बिंदुओं का योग = 1 × 44 + 5 × 20 = 44 + 100 = 144।

(c) आकृति (c) में, संख्या 32 32 बार है और संख्या 64 16 बार है। अतः सभी संख्याओं का योग = 32 × 32 + 64 × 16 = 1024 + 1024 = 2048।

(d) आकृति (d) में, 3 बिंदु (•) 17 बार हैं और 4 बिंदु (•) 18 बार हैं। अतः सभी बिंदुओं का योग = 17 × 3 + 18 × 4 = 51 + 72 = 123।

(e) आकृति (e) में, संख्या 15 22 बार है, संख्या 25 22 बार है और संख्या 35 22 बार है। अतः सभी संख्याओं का योग = 15 × 22 + 25 × 22 + 35 × 22 = 330 + 550 + 770 = 1650।

(f) आकृति (f) में, संख्या 125 18 बार है, संख्या 250 8 बार है, संख्या 500 4 बार है और संख्या 1000 1 बार है। अतः सभी संख्याओं का योग = 125 × 18 + 250 × 8 + 500 × 4 + 1000 = 2250 + 2000 + 2000 + 1000 = 7250।

पृष्ठ 69 और 70

हम कुछ सरल अनुमान करेंगे। यह एक मजेदार व्यायाम है, और आप जानकर आश्चर्यचकित हो सकते हैं कि हमारे चारों ओर विभिन्न संख्याएँ कितनी होती हैं। याद रखें, हम निम्नलिखित प्रश्नों के लिए सटीक संख्याओं में रुचि नहीं रखते हैं। कक्षा में अपने अनुमान के तरीकों को साझा करें।

Q1: चलने के लिए आप कौन से कदम उठाएंगे: (a) उस स्थान से जहां आप बैठे हैं, कक्षा के दरवाजे तक (b) स्कूल के मैदान में शुरू से अंत तक (c) आपके कक्षा के दरवाजे से स्कूल के गेट तक (d) आपके स्कूल से आपके घर तक।

उत्तर: (a) 35 कदम। (b) 600 कदम। (c) 400 कदम। (d) 10,000 कदम।

Q2. आपकी आँखें कितनी बार झपकती हैं या आप कितनी बार साँस लेते हैं: (a) एक मिनट में (b) एक घंटे में (c) एक दिन में।

उत्तर: (a) 20 बार। (b) एक मिनट में आँखें झपकने की संख्या = 20। एक घंटे में मिनटों की संख्या = 60 मिनट। एक घंटे में आँखें झपकने की संख्या = 20 × 60 = 1200। (c) एक घंटे में आँखें झपकने की संख्या = 1200। एक दिन में घंटों की संख्या = 24 घंटे। एक दिन में हम कितने घंटे सोते हैं = 7 घंटे। एक दिन में आँखें झपकने की संख्या = (24 - 7) × 1200 = 17 × 1200 = 20,400।

Q3: आपके चारों ओर कुछ वस्तुओं के नाम बताएं जो: (a) कुछ हजारों की संख्या में हैं (b) दस हजार से अधिक की संख्या में हैं।

उत्तर: (a) पेड़ की पत्तियाँ, चावल के दाने, बीज, मेवे। (b) रेत के दाने, किताब में शब्द, बालों की लटें, कपड़े में धागे, टी.वी. स्क्रीन पर पिक्सल।

30 सेकंड के भीतर अनुमान लगाने की कोशिश करें। अपने दोस्तों के साथ अपने अनुमान की जांच करें।

30 सेकंड के भीतर अनुमान लगाने की कोशिश करें। अपने दोस्तों के साथ अपने अनुमान की जांच करें।

Q1: आपके गणित की पाठ्यपुस्तक में शब्दों की संख्या: (a) 5000 से अधिक (b) 5000 से कम उत्तर: (a)

Q2: आपके स्कूल में कितने छात्र बस से स्कूल जाते हैं: (a) 200 से अधिक (b) 200 से कम उत्तर: (a)

Q3: रोशन दूध और 3 प्रकार के फल खरीदना चाहता है ताकि वह 5 लोगों के लिए फल कस्टर्ड बना सके। वह लागत का अनुमान 100 लगाता है। क्या आप उससे सहमत हैं? क्यों या क्यों नहीं? उत्तर:

दूध की अनुमानित लागत = 60
3 फलों की अनुमानित लागत = 150 (प्रत्येक फल के लिए ₹50)
कस्टर्ड पाउडर की अनुमानित लागत = 50
कस्टर्ड बनाने की कुल अनुमानित लागत = 60 + 50 + 150 = 260।

नहीं, मैं रोशन के अनुमान से सहमत नहीं हूँ क्योंकि मुझे लगता है कि 5 लोगों के लिए कस्टर्ड बनाने की लागत लगभग 260 होगी।

Q4: गांधीनगर (गुजरात) से कोहिमा (नागालैंड) के बीच की दूरी का अनुमान लगाएं। [संकेत: इन शहरों को खोजने के लिए भारत का मानचित्र देखें।] उत्तर: 3000 किमी।

पृष्ठ 71

Q5: शीटल कक्षा 6 में है और कहती है कि वह अब तक स्कूल में लगभग 13,000 घंटे बिता चुकी है। क्या आप उससे सहमत हैं? क्यों या क्यों नहीं? उत्तर:

प्रति वर्ष कुल स्कूल दिन = 210
प्रति दिन स्कूल में बिताए गए घंटे = 6 घंटे
प्रति वर्ष स्कूल में बिताए गए कुल घंटे = 210 × 6 = 1260 घंटे
कक्षा 6 तक स्कूल में बिताए गए कुल वर्ष = 8 वर्ष
इसलिए, 8 वर्षों में स्कूल में बिताए गए कुल घंटे = 1260 × 8 = 10,080 घंटे।

नहीं, मैं शीटल के इस अनुमान से सहमत नहीं हूँ कि उसने अब तक स्कूल में लगभग 13,000 घंटे बिताए हैं क्योंकि मुझे लगता है कि अधिक उचित अनुमान लगभग 10,000 घंटे होगा।

Q6: पहले, लोग लंबी दूरी तय करते थे क्योंकि उनके पास कोई अन्य परिवहन का साधन नहीं था। मान लीजिए आप अपनी सामान्य गति से चलते हैं। लगभग कितना समय लगेगा: (a) आपके वर्तमान स्थान से आपके नजदीकी पसंदीदा स्थान तक। (b) आपके वर्तमान स्थान से किसी पड़ोसी राज्य की राजधानी तक। (c) भारत के सबसे दक्षिणी बिंदु से भारत के सबसे उत्तरी बिंदु तक। उत्तर:

(a) लगभग 1 घंटे।
(b) लगभग 7-8 दिन।
(c) लगभग 100 दिन।

Q7: कुछ अनुमान लगाने वाले प्रश्न बनाएं और अपने सहपाठियों को चुनौती दें! उत्तर: छात्रों द्वारा किया जाएगा।

पृष्ठ 72

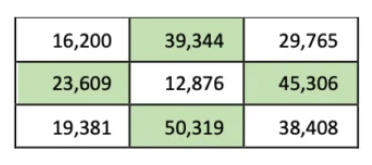
प्रश्न 1: इस ग्रिड में केवल एक सुपरसेल है (जो अपने सभी पड़ोसियों से बड़ा है)। यदि आप एक संख्या के दो अंकों को बदलते हैं, तो 4 सुपरसेल होंगे। पता करें कि कौन से अंकों को बदलना है। उत्तर: यदि आप सुपरसेल 62,871 के '6' को '1' से बदलते हैं, तो 4 सुपरसेल होंगे।

प्रश्न 2: आपके जन्म वर्ष को कपरेकर स्थिरांक तक पहुँचने में कितने राउंड लगते हैं? उत्तर: जन्म वर्ष: 2012
1st राउंड
सबसे बड़ा संख्या = 2210
सबसे छोटी संख्या = 0122
घटाना = 2210 - 0122 = 2088
2nd राउंड
सबसे बड़ा संख्या = 8820
सबसे छोटी संख्या = 0288
घटाना = 8820 - 0288
3rd राउंड
सबसे बड़ा संख्या = 8532
सबसे छोटी संख्या = 2358
घटाना = 8532 - 2358 = 6174
इसलिए, संख्या 2012 को 6174 तक पहुँचने में 3 राउंड लगते हैं, जो कपरेकर स्थिरांक है।

प्रश्न 3: हम 35,000 और 75,000 के बीच के 5-अंकीय संख्याओं का समूह हैं, जिनके सभी अंक विषम हैं। हमारे समूह में सबसे बड़ी संख्या कौन है? हमारे समूह में सबसे छोटी संख्या कौन है? हम में से 50,000 के सबसे निकट कौन है? उत्तर: 35000 और 75000 के बीच के विषम संख्याएँ हैं 35001, 35003, 35005, ……..74999। इसलिए, सबसे बड़ी संख्या = 74999, सबसे छोटी संख्या = 35001 और 50000 के निकटतम = 49999 या 50001।

प्रश्न 4: अनुमान लगाएँ कि आपको एक वर्ष में कितनी छुट्टियाँ मिलती हैं, जिसमें सप्ताहांत, त्योहार और छुट्टियाँ शामिल हैं। फिर एक सही संख्या प्राप्त करने की कोशिश करें और देखें कि आपका अनुमान कितना निकट है। उत्तर: एक वर्ष में छुट्टियों की अनुमानित संख्या, जिसमें सप्ताहांत, त्योहार और छुट्टियाँ शामिल हैं = 155 दिन
एक वर्ष में सप्ताहों की संख्या = 52 सप्ताह
रविवार की छुट्टियाँ = 52 दिन
शनिवार की छुट्टियाँ (प्रति माह 2 छुट्टियाँ) = 24
सार्वजनिक छुट्टियाँ = 15 दिन
गर्मी की छुट्टियाँ = 45 दिन
सर्दी की छुट्टियाँ = 15 दिन
एक वर्ष में वास्तविक छुट्टियों की संख्या = 52 + 24 + 15 + 45 + 15 = 151 दिन।

प्रश्न 5: एक मग, एक बाल्टी और एक ओवरहेड टैंक की क्षमता का अनुमान लगाएँ। उत्तर: एक मग की क्षमता = 0.3 लीटर
एक बाल्टी की क्षमता = 20 लीटर
एक ओवरहेड टैंक की क्षमता = 2000 लीटर।

प्रश्न 6: एक 5-अंकीय संख्या और दो 3-अंकीय संख्याएँ लिखें, जिनका योग 18,670 है। उत्तर: 5-अंकीय संख्या = 16,945
3-अंकीय संख्या = 825
3-अंकीय संख्या = 900
योग 16,945 + 825 + 900 = 18,670।

प्रश्न 7: 210 और 390 के बीच एक संख्या चुनें। एक संख्या पैटर्न बनाएं जो इस संख्या तक पहुँचने के लिए सेक्शन 3.9 में दिखाए गए समान हो। उत्तर: चुनी गई संख्या = 320
10 के मामले में: 4 × 8 × 10 = 320
20 के मामले में: 4 × 4 × 20 = 320

पृष्ठ 73

प्रश्न 8: अध्याय 1, तालिका 1 से 2 की शक्तियों का अनुक्रम याद करें। इस अनुक्रम में सभी प्रारंभिक संख्याओं के लिए कोलत्ज़ अनुमान सही क्यों है? उत्तर: 2 की शक्तियों का अनुक्रम: 1, 2, 4, 8, 16, 32, 64, ... 2 की शक्तियों का अनुक्रम सभी सम संख्याओं को शामिल करता है। जब हम एक सम संख्या को 2 से विभाजित करते हैं, तो हमें एक सम संख्या मिलेगी, लेकिन लगातार सम संख्या को 2 से विभाजित करने पर हम अंततः 1 पर पहुँचेंगे। यही कारण है कि कोलत्ज़ अनुमान इस अनुक्रम में सभी प्रारंभिक संख्याओं के लिए सही है। उदाहरण: 16 (2 की शक्ति) 16/2 = 8 8/2 = 4 4/2 = 2 2/2 = 1

प्रश्न 9: जांचें कि क्या कोलत्ज़ अनुमान प्रारंभिक संख्या 100 के लिए सही है। उत्तर: कोलत्ज़ अनुमान: यदि संख्या सम है, तो इसका आधा लें; यदि संख्या विषम है, तो इसे 3 से गुणा करें और 1 जोड़ें। यदि आप ऐसा करते रहें, तो आप हमेशा संख्या 1 तक पहुँचेंगे, चाहे आप जिस संख्या से शुरू करें। 100 (सम): 100/2 = 50 50 (सम): 50/2 = 25 25 (विषम): 25 x 3 + 1 = 76 76 (सम): 76/2 = 38 38 (सम): 38/2 = 19 19 (विषम): 19 x 3 + 1 = 58 58 (सम): 58/2 = 29 29 (विषम): 29 x 3 + 1 = 88 88 (सम): 88/2 = 44 44 (सम): 44/2 = 22 22 (सम): 22/2 = 11 11 (विषम): 11 x 3 + 1 = 34 34 (सम): 34/2 = 17 17 (विषम): 17 x 3 + 1 = 52 52 (सम): 52/2 = 26 26 (सम): 26/2 = 13 13 (विषम): 13 x 3 + 1 = 40 40 (सम): 40/2 = 20 20 (सम): 20/2 = 10 10 (सम): 10/2 = 5 5 (विषम): 5 x 3 + 1 = 16 16 (सम): 16/2 = 8 8 (सम): 8/2 = 4 4 (सम): 4/2 = 2 2 (सम): 2/2 = 1

प्रश्न 10: 0 से शुरू करते हुए, खिलाड़ी 1 से 3 के बीच संख्याएँ जोड़ते हैं। जो पहला व्यक्ति 22 तक पहुँचेगा, वह जीत जाएगा। अब जीतने की रणनीति क्या है? उत्तर:

(i) अपने पहले टर्न में 3 जोड़कर 3 तक पहुँचें।
(ii) फिर, हमेशा इस तरह से चलें कि आप विरोधी को 4 के गुना पर छोड़ें।
(iii) इस रणनीति का पालन करने से यह सुनिश्चित होगा कि आप पहले 22 तक पहुँचें, जिससे जीत सुनिश्चित होगी।

पृष्ठ 59

The document संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: NCERT Solutions: संख्या खेल for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for NCERT Solutions: संख्या खेल have been prepared according to the Class 6 exam syllabus. Information about NCERT Solutions: संख्या खेल covers topics like 30 सेकंड के भीतर अनुमान लगाने की कोशिश करें। अपने दोस्तों के साथ अपने अनुमान की जांच करें। and NCERT Solutions: संख्या खेल Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions: संख्या खेल.

Introduction of NCERT Solutions: संख्या खेल in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & NCERT Solutions: संख्या खेल in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about NCERT Solutions: संख्या खेल

In this doc you can find the meaning of NCERT Solutions: संख्या खेल defined & explained in the simplest way possible. Besides explaining types of NCERT Solutions: संख्या खेल theory, EduRev gives you an ample number of questions to practice NCERT Solutions: संख्या खेल tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

Extra Questions

Exam

mock tests for examination

Objective type Questions

video lectures

study material

practice quizzes

Semester Notes

Previous Year Questions with Solutions

ppt

shortcuts and tricks

संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Sample Paper

Free

pdf

Summary

संख्या खेल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

MCQs

Viva Questions

Important questions

past year papers

;

Additional Information about NCERT Solutions: संख्या खेल for Class 6 Preparation

NCERT Solutions: संख्या खेल Free PDF Download

The NCERT Solutions: संख्या खेल is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the NCERT Solutions: संख्या खेल now and kickstart your journey towards success in the Class 6 exam.

Importance of NCERT Solutions: संख्या खेल

The importance of NCERT Solutions: संख्या खेल cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

NCERT Solutions: संख्या खेल Notes

NCERT Solutions: संख्या खेल Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to NCERT Solutions: संख्या खेल. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions: संख्या खेल Notes on EduRev are your ultimate resource for success.

NCERT Solutions: संख्या खेल Class 6 Questions

The "NCERT Solutions: संख्या खेल Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study NCERT Solutions: संख्या खेल on the App

Students of Class 6 can study NCERT Solutions: संख्या खेल alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the NCERT Solutions: संख्या खेल, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of NCERT Solutions: संख्या खेल is prepared as per the latest Class 6 syllabus.

Education Revolution