Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > Word Problems: संख्या खेल

Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

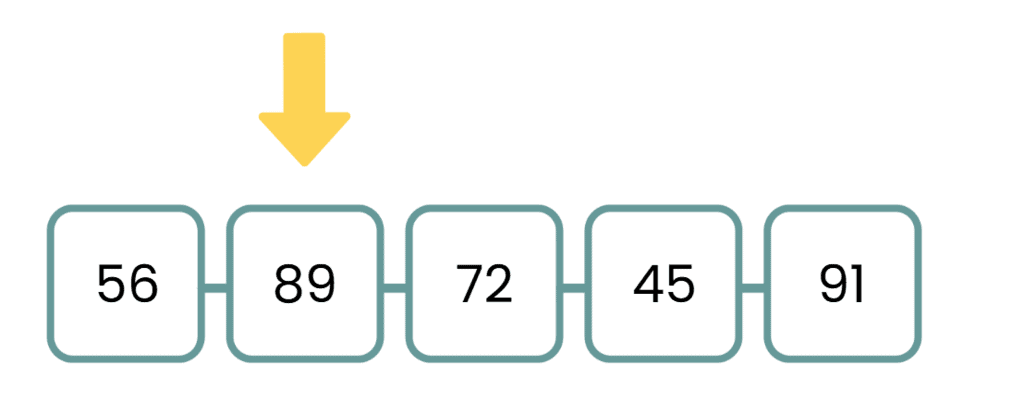
प्रश्न 1: एक विज्ञान मेले में, छात्र अपनी परियोजना के स्कोर को एक पंक्ति में प्रदर्शित करते हैं: 56, 89, 72, 45, 91। जब कोई स्कोर उसके तुरंत बाएँ और दाएँ स्कोर से अधिक होता है, तो उसे \"सुपरसेल\" कहा जाता है। कौन सा स्कोर सुपरसेल है? समाधान: आइए प्रत्येक स्कोर की तुलना उसके बाएँ और दाएँ पड़ोसियों से करें:

56: पहला नंबर, केवल दाएँ पड़ोसी (89) है। चूंकि 56 < 89="" →="" सुपरसेल="" नहीं="" />
89: बाएँ = 56, दाएँ = 72 → 89 > 56 और 89 > 72 → सुपरसेल।
72: बाएँ = 89, दाएँ = 45 → 72 < 89="" →="" सुपरसेल="" नहीं="" />
45: बाएँ = 72, दाएँ = 91 → 45 < 72="" →="" सुपरसेल="" नहीं="" />
91: अंतिम नंबर, केवल बाएँ पड़ोसी (45) है। 91 > 45 लेकिन कोई दाएँ पड़ोसी नहीं → सुपरसेल नहीं है।

उत्तर: 89 सुपरसेल है।

Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 2: प्रिया स्कोर को एक संख्या रेखा पर रख रही है: 1240, 3780, 950, 5200, 8900। संख्या रेखा 0 से 10,000 तक है। कौन सा स्कोर 4000 के सबसे निकट है? समाधान: प्रत्येक स्कोर से 4000 का पूर्ण अंतर ज्ञात करें:

|4000 - 1240| = 2760
|4000 - 3780| = 220
|4000 - 950| = 3050
|4000 - 5200| = 1200
|4000 - 8900| = 4900

सबसे छोटा अंतर 220 है। उत्तर: 3780 4000 के सबसे निकट है।

प्रश्न 3: रोहन एक 3-अंक संख्या खोजना चाहता है, जिसका अंक योग 273 के अंक योग के बराबर हो। ऐसी एक संख्या क्या है? समाधान: 273 का अंक योग = 2 + 7 + 3 = 12 उदाहरण: 156 → 1 + 5 + 6 = 12 उत्तर: ऐसी एक संख्या 156 है।

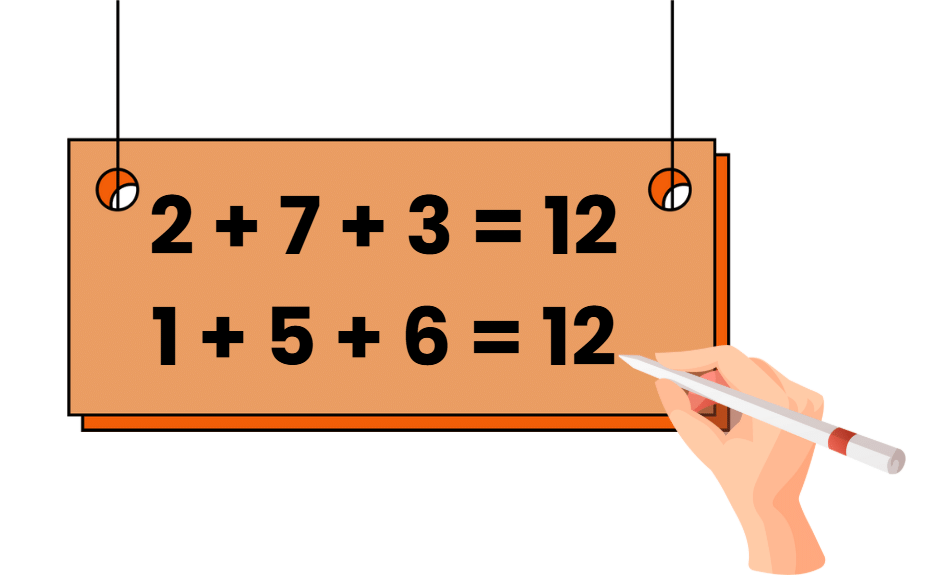
प्रश्न 4: सारा यह गिनती करती है कि अंक 5 1 से 50 के बीच कितनी बार आता है। यह कितनी बार आता है? समाधान: उन संख्याओं की गिनती करें जहाँ 5 आता है:

एकक स्थान: 5, 15, 25, 35, 45 → 5 बार
दहाई स्थान: 50 → 1 बार

कुल = 5 + 1 = 6 उत्तर: अंक 5 6 बार आता है।

प्रश्न 5: नेहा अंकों 2, 3, और 4 का उपयोग करके सभी 3-अंकीय पलिंड्रोम की सूची बनाती है। ऐसे कितने पलिंड्रोम हैं? समाधान: एक 3-अंकीय पलिंड्रोम का रूप ABA होता है।

A (पहला और आखिरी अंक) के लिए 3 विकल्प हैं: 2, 3, या 4
B (मध्य अंक) के लिए भी 3 विकल्प हैं।

कुल = 3 × 3 = 9 उत्तर: ऐसे 9 पलिंड्रोम हैं।

प्रश्न 6: विकास 56 के साथ रिवर्स-एंड-ऐड विधि का प्रयास करता है। वह कौन सा पहला पलिंड्रोम प्राप्त करता है? समाधान:

56 को पलटें → 65
जोड़ें: 56 + 65 = 121 (एक पलिंड्रोम)

उत्तर: पहला पलिंड्रोम 121 है।

प्रश्न 7: आर्यन संख्या 5281 पर कप्रेकर प्रक्रिया लागू करता है। एक चरण के बाद परिणाम क्या है? समाधान:

अंक को अवरोही क्रम में व्यवस्थित करें: 8521
अंक को आरोही क्रम में व्यवस्थित करें: 1258
घटाएं: 8521 - 1258 = 7263

उत्तर: परिणाम 7263 है।

प्रश्न 8: कुनाल यह गिनना चाहता है कि अंक 3 1 से 200 तक के अंकों में कितनी बार आता है। समाधान:

इकाइयों का स्थान: 3, 13, 23, ..., 193 → 20 अंक
दशमलव स्थान: 30–39 और 130–139 → 10 + 10 = 20 अंक

कुल उपस्थिति = 20 (इकाइयों) + 20 (दशमलव) = 40

उत्तर: अंक 3 कुल 40 बार आता है।

प्रश्न 9: रिया अपनी घड़ी देखती है और एक पलिंड्रोम समय नोट करती है, जैसे 3:33। 12 घंटे की घड़ी अवधि में ऐसे कितने पलिंड्रोम समय होते हैं? समाधान: एक पलिंड्रोम समय वह होता है जो आगे और पीछे पढ़ने पर समान दिखता है।

पलिंड्रोम समय जैसे AA:AA → 1:11, 2:22, 3:33, 4:44, 5:55 (5 बार)
AB:BA रूप → 10:01, 11:11, 12:21 (3 बार)

तो, एक 12 घंटे की अवधि (AM या PM) में, कुल पलिंड्रोम समय: 5 (चरण 1 से) + 3 (चरण 2 से) = 8

लेकिन याद रखें: 12-घंटे का घड़ी दिन में दो बार दोहराता है — एक बार AM में और एक बार PM में।

तो, 24 घंटे में कुल पलिंड्रोमिक समय:

8 (AM) 8 (PM) = 16

उत्तर: कुल 16 पलिंड्रोमिक समय हैं।

प्रश्न 10: कवी 30,000, 800, और 600 का उपयोग करके 28,600 प्राप्त करने के लिए घटाता है, प्रत्येक का उपयोग अधिकतम एक बार करता है। गणना क्या है? समाधान: 30,000 से शुरू करें। 800 घटाएं: 30,000 - 800 = 29,200 फिर 600 घटाएं: 29,200 - 600 = 28,600 उत्तर: 28,600 = 30,000 - 800 - 600

प्रश्न 11: अरव 14 से शुरू करता है और कॉलैट्ज़ अनुमान नियमों (सम संख्या ÷ 2, विषम संख्या × 3 + 1) को लागू करता है। 1 तक पहुँचने तक अनुक्रम क्या है? समाधान: 14 → 7 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 उत्तर: अनुक्रम है 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1।

प्रश्न 12: 3×3 ग्रिड में परीक्षण अंकों में सुपरसेल(s) की पहचान करें:

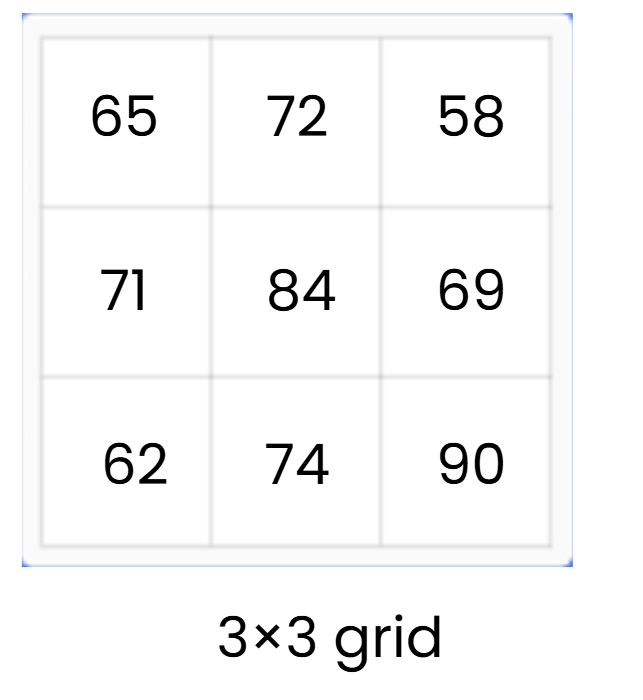
एक सुपरसेल अपने पड़ोसियों (ऊपर, नीचे, बाएं, और दाएं) से बड़ा होता है। समाधान:

प्रत्येक सेल की जांच करें और सभी 4 पड़ोसियों के साथ तुलना करें:

(1,1) = 65: पड़ोसी = 72 (दाएं), 71 (नीचे)। 65 < 72="" →="" सुपरसेल="" />
(1,2) = 72: पड़ोसी = 65 (बाएं), 58 (दाएं), 84 (नीचे)। 72 < 84="" →="" सुपरसेल="" />
(1,3) = 58: पड़ोसी = 72 (बाएं), 69 (नीचे)। 58 < 72="" →="" सुपरसेल="" />
(2,1) = 71: पड़ोसी = 65 (ऊपर), 84 (दाएं), 62 (नीचे)। 71 < 84="" →="" सुपरसेल="" />
(2,2) = 84: पड़ोसी = 72 (ऊपर), 71 (बाएं), 69 (दाएं), 77 (नीचे)। 84 > सभी → सुपरसेल।
(2,3) = 69: पड़ोसी = 58 (ऊपर), 84 (बाएं), 90 (नीचे)। 69 < 84="" →="" सुपरसेल="" />
(3,1) = 62: पड़ोसी = 71 (ऊपर), 77 (दाएं)। 62 < 71="" →="" सुपरसेल="" />
(3,2) = 77: पड़ोसी = 84 (ऊपर), 62 (बाएं), 90 (दाएं)। 77 < 84="" →="" सुपरसेल="" />
(3,3) = 90: पड़ोसी = 69 (ऊपर), 77 (बाएं)। 90 > दोनों → लेकिन सभी 4 पड़ोसी नहीं → सुपरसेल नहीं।

उत्तर: 84 सुपरसेल है।

प्रश्न 13: प्रियंक एक जार में कैंडी की संख्या का अनुमान लगाता है। प्रत्येक मुट्ठी में लगभग 20 कैंडी होती हैं, और वह 15 मुट्ठियों की गिनती करता है। जार में लगभग कितनी कैंडी हैं? समाधान: कैंडी की संख्या = 20 × 15 = 300 उत्तर: जार में लगभग 300 कैंडी हैं।

प्रश्न 14: एक खेल में, खिलाड़ी बारी-बारी से 1 से 4 तक का एक नंबर जोड़ते हैं, जिसका लक्ष्य 20 तक पहुँचना है। माया जीतने के लिए 20 तक पहुँचने के लिए क्या संख्या छोड़ना चाहती है? समाधान: 20 से पीछे की ओर काम करते हुए 4 के कदमों का उपयोग करें: 20 → 16 → 12 → 8 → 4 जीतने के लिए, माया को कुल को 16 पर छोड़ने का लक्ष्य रखना चाहिए। इस तरह, विपक्षी द्वारा जो भी जोड़ा जाए (1 से 4), माया सही संख्या जोड़कर 20 तक पहुँच सकती है। उत्तर: माया को कुल को 16 पर छोड़ने का लक्ष्य रखना चाहिए।

प्रश्न 15: अनिका उलटने और जोड़ने की विधि से 78 से शुरू करती है। पलिंड्रोम तक पहुँचने के लिए कितने कदम आवश्यक हैं? समाधान: उलटने और जोड़ने की विधि में, हम एक संख्या लेते हैं, उसके अंकों को उलटते हैं, दोनों संख्याओं को जोड़ते हैं, और तब तक कदम दोहराते हैं जब तक हमें पलिंड्रोम नहीं मिल जाता। पलिंड्रोम एक संख्या है जो आगे और पीछे समान पढ़ी जाती है (जैसे 121, 1331, या 4884)।

आइए 78 से शुरुआत करें और कदमों का पालन करें:

कदम 1: मूल संख्या = 78 उलटी संख्या = 87 योग: 78 + 87 = 165

कदम 2: मूल संख्या = 165 उलटी संख्या = 561 योग: 165 + 561 = 726

कदम 3: मूल संख्या = 726 उलटी संख्या = 627 योग: 726 + 627 = 1353

कदम 4: मूल संख्या = 1353 उलटी संख्या = 3531 योग: 1353 + 3531 = 4884

4884 एक पलिंड्रोम है, इसलिए हम यहाँ रुकते हैं।

उत्तर: उलटने और जोड़ने की विधि का उपयोग करके 78 से शुरू करके पलिंड्रोम तक पहुँचने में 4 कदम लगते हैं।

प्रश्न 16: अर्जुन एक संख्या रेखा पर बिंदुओं को अंकित करता है: 2300, 4500, 6700, 8900। वह 2300 और 6700 के बीच में एक नया बिंदु रखना चाहता है। इस बिंदु का मान क्या होगा? हल: मध्य बिंदु = (2300 + 6700) ÷ 2 = 9000 ÷ 2 = 4500 उत्तर: नया बिंदु 4500 है।

प्रश्न 17: लिला 9 पर कॉलत्ज़ अनुमान लागू करती है। 1 तक पहुँचने के लिए कितने चरणों की आवश्यकता है? हल: 9 → 28 → 14 → 7 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 कुल 19 चरण हैं। उत्तर: यह 19 चरण लेता है।

The document Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: Word Problems: संख्या खेल for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for Word Problems: संख्या खेल have been prepared according to the Class 6 exam syllabus. Information about Word Problems: संख्या खेल covers topics like and Word Problems: संख्या खेल Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Word Problems: संख्या खेल.

Introduction of Word Problems: संख्या खेल in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & Word Problems: संख्या खेल in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about Word Problems: संख्या खेल

In this doc you can find the meaning of Word Problems: संख्या खेल defined & explained in the simplest way possible. Besides explaining types of Word Problems: संख्या खेल theory, EduRev gives you an ample number of questions to practice Word Problems: संख्या खेल tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

MCQs

Sample Paper

Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Semester Notes

Important questions

Free

Objective type Questions

video lectures

practice quizzes

Summary

shortcuts and tricks

Extra Questions

past year papers

Exam

ppt

Previous Year Questions with Solutions

Viva Questions

Word Problems: संख्या खेल | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

pdf

mock tests for examination

study material

;

Additional Information about Word Problems: संख्या खेल for Class 6 Preparation

Word Problems: संख्या खेल Free PDF Download

The Word Problems: संख्या खेल is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Word Problems: संख्या खेल now and kickstart your journey towards success in the Class 6 exam.

Importance of Word Problems: संख्या खेल

The importance of Word Problems: संख्या खेल cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Word Problems: संख्या खेल Notes

Word Problems: संख्या खेल Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Word Problems: संख्या खेल. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Word Problems: संख्या खेल Notes on EduRev are your ultimate resource for success.

Word Problems: संख्या खेल Class 6 Questions

The "Word Problems: संख्या खेल Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Word Problems: संख्या खेल on the App

Students of Class 6 can study Word Problems: संख्या खेल alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Word Problems: संख्या खेल, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Word Problems: संख्या खेल is prepared as per the latest Class 6 syllabus.

Education Revolution