प्राइम टाइम Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

परिचय

इस अध्याय में, हम संख्याओं की दुनिया की खोज करेंगे और समझेंगे कि उन्हें विभिन्न तरीकों से विभाजित और गुणा कैसे किया जा सकता है। हम प्राइम नंबर (असाधारण संख्याएँ), कॉम्पोज़िट नंबर (संयोजित संख्याएँ) के बारे में जानेंगे और कैसे ये अवधारणाएँ हमें गणित में समस्याएँ हल करने में मदद करती हैं। इस अध्याय के अंत तक, आप प्राइम नंबरों की पहचान कर सकेंगे, गुणक और बहुगुणकों के महत्व को समझेंगे, और इन अवधारणाओं का उपयोग पहेलियाँ और खेल खेलने में कर सकेंगे।

सामान्य बहुगुणक और सामान्य गुणांक

• सामान्य बहुगुणक: ये ऐसे नंबर हैं जो दो या दो से अधिक संख्याओं के बहुगुणक होते हैं। उदाहरण के लिए, 3 और 5 के सामान्य बहुगुणक 15, 30, 45, आदि हैं। ये संख्याएँ खास होती हैं क्योंकि इन्हें 3 और 5 दोनों से बिना कोई शेष के विभाजित किया जा सकता है।
• सामान्य गुणांक: ये ऐसे नंबर हैं जो दो या दो से अधिक संख्याओं को बिना शेष के सही तरीके से विभाजित करते हैं। उदाहरण के लिए, 14 और 36 के सामान्य गुणांक 1 और 2 हैं।

एक उदाहरण के साथ सामान्य बहुगुणक को समझना

उदाहरण: इडली-वड़ा खेल कल्पना करें कि आप अपने दोस्तों के साथ एक सर्कल में बैठे हैं, और आप सभी एक खेल खेल रहे हैं जिसे "इडली-वड़ा" कहा जाता है। नियम सरल हैं:

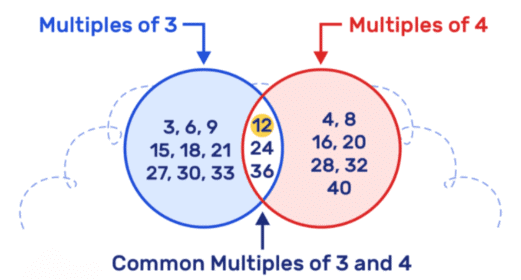
पहला खिलाड़ी \"1\" कहता है, अगला \"2\" कहता है, और इसी तरह आगे बढ़ते हैं। लेकिन जब संख्या 3 का गुणांक (जैसे 3, 6, 9...) कहने का समय आता है, तो खिलाड़ी संख्या कहने के बजाय \"इडली\" कहता है। जब संख्या 5 का गुणांक (जैसे 5, 10, 15...) कहने का समय आता है, तो खिलाड़ी \"वड़ा\" कहता है। यदि संख्या 3 और 5 दोनों का गुणांक है (जैसे 15, 30...), तो खिलाड़ी \"इडली-वड़ा!\" कहता है।

खेल तब तक जारी रहता है जब तक कोई गलती नहीं करता, और आखिरी बचे हुए खिलाड़ी की जीत होती है।

खेल को समझना: सामान्य गुणांक

अब, चलिए देखते हैं कि खेल में क्या हो रहा है।

• 3 के गुणांक: ये संख्या जैसे 3, 6, 9, 12... हैं जहाँ आप \"इडली\" कहते हैं।
• 5 के गुणांक: ये संख्या जैसे 5, 10, 15, 20... हैं जहाँ आप \"वड़ा\" कहते हैं।
• 3 और 5 के सामान्य गुणांक: ये विशेष संख्या जैसे 15, 30, 45... हैं जहाँ आप \"इडली-वड़ा\" कहते हैं क्योंकि वे दोनों 3 और 5 के गुणांक हैं।

खेल में, जब आप \"इडली\" या \"वड़ा\" कहते हैं, तो आप 3 और 5 के गुणांकों को पहचान रहे हैं। जब आप \"इडली-वड़ा\" कहते हैं, तो आप उन संख्याओं की पहचान कर रहे हैं जो 3 और 5 दोनों के साझा गुणांक हैं।

सामान्य गुणांक को एक उदाहरण के साथ समझना

उदाहरण: जंप जैकपॉट

अब, चलिए एक और खेल \"जंप जैकपॉट\" के बारे में जानते हैं। यह इस प्रकार काम करता है:

• ग्राम्पी एक संख्या, जैसे 24, पर एक खजाना छिपाता है।
• जम्पी केवल उस संख्या के गुणांकों पर ही उतर सकता है जो वह चुनता है (जैसे 4, 6, या 12)।
• जीतने के लिए, जम्पी को ठीक 24 पर उतरना होगा।

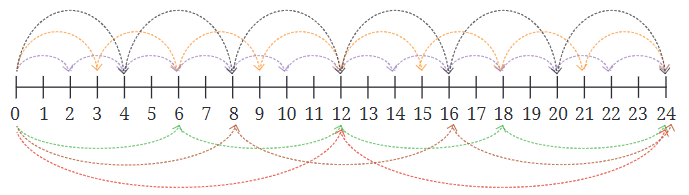
उदाहरण के लिए, यदि जम्पी 4 चुनता है, तो वह 4, 8, 12, 16, 20, 24... पर उतरता है और खजाना जीतता है! यदि वह 6 या 12 चुनता है, तो वह भी जीतता है क्योंकि ये संख्या 24 के गुणांक हैं।

लेकिन अगर दो खजाने हों तो क्या होगा? मान लीजिए एक 14 पर है और दूसरा 36 पर। जंपि को ऐसा नंबर चुनना होगा जो उसे दोनों पर लैंड करने की अनुमति दे। अगर वह 7 चुनता है, तो वह 14 पर लैंड करता है लेकिन 36 को चूक जाता है। हालांकि, अगर वह 2 चुनता है, तो वह दोनों 14 और 36 पर लैंड कर जाता है, दोनों खजाने जीतता है।

खेल को समझना: सामान्य गुणांक
"जंप जैकपॉट" में, जब जंपि सफलतापूर्वक दोनों खजानों पर लैंड करता है, तो वह एक सामान्य गुणांक का उपयोग कर रहा है।

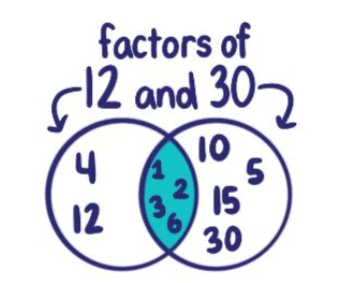
• 14 के गुणांक: ये नंबर हैं 1, 2, 7, और 14।
• 36 के गुणांक: ये नंबर हैं 1, 2, 3, 4, 6, 9, 12, 18, और 36।
• 14 और 36 के सामान्य गुणांक: ये वे नंबर हैं जो 14 और 36 दोनों को पूरी तरह विभाजित कर सकते हैं, जैसे 1 और 2।

अप्राइम नंबर

• अप्राइम नंबर: एक अप्राइम नंबर वह होता है जो 1 से बड़ा होता है और केवल 1 और अपने आप से ही विभाजित हो सकता है। उदाहरण के लिए, 7 एक अप्राइम नंबर है क्योंकि 7 को केवल 1 और 7 से ही पूरी तरह विभाजित किया जा सकता है।
• संयोजित नंबर: एक संयोजित नंबर वह होता है जिसके दो से अधिक गुणांक होते हैं। इसका मतलब है कि इसे 1, अपने आप और कम से कम एक अन्य नंबर से पूरी तरह विभाजित किया जा सकता है। उदाहरण के लिए, 12 संयोजित है क्योंकि इसे 1, 2, 3, 4, 6, और 12 से विभाजित किया जा सकता है।

संख्या 1 न तो अप्राइम है और न ही संयोजित संख्या है।

प्राइम नंबर और समग्र संख्या को समझना उदाहरणों के साथ

उदाहरण 1: अंजीर पैकिंग खेल

गुणा और अंशु अपने खेत से अंजीर पैक करना चाहते हैं। गुणा हर डिब्बे में 12 अंजीर रखना चाहता है, जबकि अंशु 7 अंजीर हर डिब्बे में रखना चाहता है। वे अंजीरों को आयताकार आकार में व्यवस्थित करना शुरू करते हैं:

• गुणा की व्यवस्था: गुणा 12 अंजीरों को कई तरीकों से व्यवस्थित कर सकता है, जैसे 2 पंक्तियों में 6 अंजीर (2 × 6) या 3 पंक्तियों में 4 अंजीर (3 × 4)। इसका कारण यह है कि 12 के कई कारक होते हैं।
• अंशु की व्यवस्था: अंशु केवल 7 अंजीरों को एक ही तरीके से व्यवस्थित कर सकता है: 1 पंक्ति में 7 अंजीर या 7 पंक्तियों में 1 अंजीर। इसका कारण यह है कि 7 के केवल दो कारक होते हैं।

सिद्धांतों को समझना

• कारक: यह खेल हमें दिखाता है कि जैसे 12 को कई तरीकों से व्यवस्थित किया जा सकता है क्योंकि इसके कई कारक होते हैं (जैसे, 12 = 2 × 6 या 3 × 4)। जबकि 7 को केवल एक ही तरीके से व्यवस्थित किया जा सकता है, इसके पास केवल दो कारक होते हैं (1 और वह संख्या स्वयं)।
• प्राइम नंबर: अंशु की 7 अंजीर केवल एक ही तरीके से व्यवस्थित की जा सकती हैं क्योंकि 7 एक प्राइम नंबर है। एक प्राइम नंबर के ठीक दो कारक होते हैं: 1 और वह संख्या स्वयं। प्राइम नंबर के उदाहरण हैं: 2, 3, 5, 7, 11, और 13।
• समग्र संख्या: गुणा की 12 अंजीर को कई तरीकों से व्यवस्थित किया जा सकता है क्योंकि 12 एक समग्र संख्या है। एक समग्र संख्या के दो से अधिक कारक होते हैं। उदाहरणों में 4, 6, 8, 9, और 12 शामिल हैं।

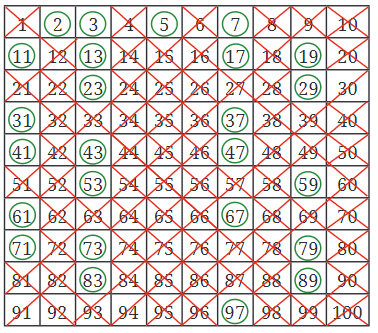
उदाहरण 2: प्राइम नंबर खोजना: एराटोस्थेनेस की छाननी

1 से 100 के बीच प्राइम नंबर खोजने के लिए, आप एराटोस्थेनेस की छाननी नामक एक विधि का उपयोग कर सकते हैं:

• 1 को काट दें क्योंकि यह न तो प्राइम है और न ही समग्र।
• 2 को घेरें (पहला प्राइम नंबर), फिर 2 के सभी गुणांक को काट दें (जैसे 4, 6, 8...)।
• 3 को घेरें (अगला प्राइम नंबर), फिर 3 के सभी गुणांक को काट दें (जैसे 6, 9, 12...)।
• 5 को घेरें और 5 के सभी गुणांक को काट दें (जैसे 10, 15, 20...)।
• जब तक सभी नंबर या तो घेराए या काटे नहीं जाते, इस प्रक्रिया को जारी रखें।

घेराए गए नंबर प्राइम हैं, और काटे गए नंबर (1 को छोड़कर) समग्र हैं। यह विधि आपको 100 तक सभी प्राइम नंबर जल्दी से खोजने में मदद करती है।

युगों के माध्यम से प्रमुख संख्याएँ

• प्रमुख संख्याएँ सभी पूर्ण संख्याओं के लिए मूलभूत निर्माण खंड की तरह हैं। प्राचीन समय से, 2000 साल पहले से, गणितज्ञ प्रमुख संख्याओं के रहस्यों को समझने की कोशिश कर रहे हैं, और वे आज भी इस पर काम कर रहे हैं!
• एक दिलचस्प प्रश्न है कि क्या कोई सबसे बड़ी प्रमुख संख्या है या इनकी संख्या अनंत है। एक प्रसिद्ध गणितज्ञ, यूक्लिड, ने इस प्रश्न का उत्तर बहुत पहले खोजा था, और आप इसे एक बाद की कक्षा में सीखेंगे।
• यहाँ एक मजेदार तथ्य है: सबसे बड़ी प्रमुख संख्या जो कभी भी लिखी गई है, इतनी विशाल है कि इसे हाथ से लिखने में लगभग 6500 पृष्ठ लगेंगे! इसके आकार के कारण, लोग इसे केवल कंप्यूटर पर रख सकते हैं।

खजाने की सुरक्षा के लिए सह-प्रमुख संख्याएँ

सह-प्रमुख संख्याएँ वे दो संख्याएँ होती हैं जिनके पास 1 के अलावा कोई सामान्य गुणक नहीं होता। इसका मतलब है कि इन्हें 1 के अलावा किसी भी समान संख्या से विभाजित नहीं किया जा सकता।

उदाहरण के साथ सह-प्रमुख को समझना

कल्पना कीजिए कि आपके दो दोस्त हैं, एलिस और बॉब, जो विभिन्न प्रकार की गेंदों का संग्रह करना पसंद करते हैं। एलिस के पास 7 गेंदों का एक थैला है, और बॉब के पास 9 गेंदों का एक थैला है। वे अपनी गेंदों को समान समूहों में बाँटना चाहते हैं, लेकिन एक शर्त है: वे सुनिश्चित करना चाहते हैं कि किसी भी एक समूह में दोनों थैलों से समान संख्या की गेंदें न हों।

अब, चलिए देखते हैं कि क्या वे ऐसा कर सकते हैं। अगर हम गेंदों को समूहों में बांटने की कोशिश करते हैं, तो हमें एक दिलचस्प बात का पता चलता है: 7 और 9 के पास कोई ऐसा सामान्य संख्या नहीं है जो उन्हें समान रूप से बांट सके, सिवाय 1 के। इसका मतलब है कि ऐलिस और बॉब ऐसे समूह नहीं बना सकते जहाँ दोनों के पास समान संख्या में गेंदें हों।

इसलिए, इस मामले में, 7 और 9 को को-प्राइम संख्या कहा जाता है क्योंकि वे 1 को छोड़कर कोई सामान्य गुणांक साझा नहीं करते हैं।

इसे और सरल बनाने के लिए, को-प्राइम संख्याओं को दो दोस्तों की तरह समझें जो अलग-अलग चीज़ों को पसंद करते हैं और उनके पास कुछ भी सामान्य नहीं है, सिवाय इसके कि वे दोनों आइसक्रीम पसंद करते हैं (जो इस मामले में संख्या 1 के समान है)।

एक और उदाहरण हो सकता है 8 और 15। ये संख्याएँ भी को-प्राइम हैं क्योंकि 1 को छोड़कर और कोई संख्या नहीं है जो 8 और 15 दोनों को समान रूप से बांट सके। ऐलिस और बॉब की तरह, इन संख्याओं के पास भी कुछ और सामान्य नहीं है!

खजाने को सुरक्षित रखना

को-प्राइम गुणांक एक गुप्त कोड की तरह होते हैं जो खजानों को सुरक्षित रखते हैं। यदि दो संख्याएँ 1 को छोड़कर कोई गुणांक साझा नहीं करती हैं, तो उन्हें को-प्राइम कहा जाता है। इसका मतलब है कि यदि आप इन संख्याओं पर खजाने रखते हैं, तो कोई भी व्यक्ति जो समान कूदने के आकार (1 को छोड़कर) से इन तक पहुँचने का प्रयास करेगा, नहीं पहुँच सकेगा, जिससे यह आपके खजानों के लिए एक आदर्श छिपने की जगह बन जाती है!

को-प्राइम कला

कल्पना कीजिए कि आपके पास एक वृत्त है जिसके चारों ओर खूंटे लगे हैं, जैसे एक घड़ी का चेहरा। आप एक खूंटे पर एक धागा बांधते हैं और फिर कुछ खूंटों को छोड़कर अगले खूंटे पर धागा बांधते हैं। इसे “धागा-फासला” कहा जाता है।

अब, चलिए कुछ उदाहरणों पर नज़र डालते हैं ताकि समझ सकें कि यह कैसे काम करता है:

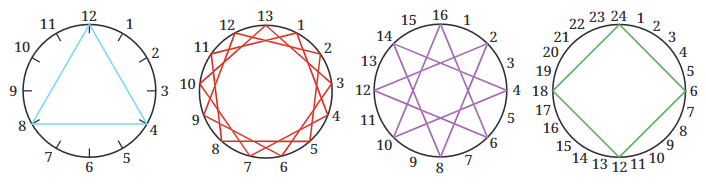
15 पेग्स, थ्रेड-गैप 10: कल्पना करें कि आपके पास एक वृत्त में 15 पेग्स हैं। आप पहले पेग पर धागा बांधते हैं, 10 पेग्स को छोड़ते हैं, और अगले पेग पर धागा बांधते हैं। आप इसे तब तक करते रहते हैं जब तक आप पहले पेग पर वापस नहीं आते। चूंकि 15 और 10 में आम गुणांक (5) होते हैं, धागा हर पेग को नहीं छुएगा। यह एक पैटर्न बनाएगा जिसमें कुछ पेग्स छोड़ दिए जाएंगे।

10 पेग्स, थ्रेड-गैप 7: अब आपके पास 10 पेग्स हैं, और आप हर बार 7 पेग्स छोड़ते हैं जब आप धागा बांधते हैं। 10 और 7 सह-प्राइम हैं (इनका कोई सामान्य गुणांक नहीं है सिवाय 1 के)। इसलिए, धागा अंततः हर पेग को छू लेगा, जिससे एक पूर्ण पैटर्न बनेगा।

14 पेग्स, थ्रेड-गैप 6: यहाँ, आपके पास 14 पेग्स हैं और आप हर बार 6 पेग्स छोड़ते हैं। चूंकि 14 और 6 में आम गुणांक (2) होते हैं, धागा हर पेग को नहीं छू पाएगा, और पैटर्न में कुछ पेग्स छोड़ दिए जाएंगे।

8 पेग्स, थ्रेड-गैप 3: आपके पास 8 पेग्स हैं और आप हर बार 3 पेग्स छोड़ते हैं। 8 और 3 सह-प्राइम हैं, इसलिए धागा अंततः हर पेग को छू लेगा, जिससे एक पूर्ण पैटर्न बनेगा।

यहाँ क्या हो रहा है?

जब पेग्स की संख्या और थ्रेड-गैप सह-प्राइम होते हैं (जैसे 10 और 7 या 8 और 3), तो धागा हर पेग को छूता है, जिससे एक पूर्ण पैटर्न बनता है। लेकिन जब वे सह-प्राइम नहीं होते (जैसे 15 और 10 या 14 और 6), तो धागा कुछ पेग्स छोड़ देता है, और आपको एक पूर्ण पैटर्न नहीं मिलता।

प्राइम फैक्टराइजेशन

• जब हम किसी संख्या को उसके व्यक्तिगत गुणकों में तोड़ते हैं, तो उन गुणकों को प्राइम फैक्टर्स कहा जाता है यदि वे प्राइम नंबर हैं। उदाहरण के लिए, 56 के प्राइम फैक्टर्स 2 और 7 हैं क्योंकि दोनों प्राइम नंबर हैं।
• 1 से बड़ी हर संख्या को प्राइम फैक्टर्स में तोड़ा जा सकता है, जिसे प्राइम फैक्टराइजेशन कहा जाता है। इसमें सम संख्याओं को उनके गुणकों में तब तक तोड़ना शामिल है जब तक कि केवल प्राइम नंबर न रह जाएं।
• संख्या 1 का प्राइम फैक्टराइजेशन नहीं होता क्योंकि यह किसी भी प्राइम नंबर द्वारा विभाज्य नहीं है। प्राइम फैक्टराइजेशन केवल 1 से बड़ी संख्याओं पर लागू होता है।

एक उदाहरण के साथ प्राइम फैक्टराइजेशन को समझना

कल्पना कीजिए कि आपके पास कई मिठाइयाँ हैं, और प्रत्येक मिठाई का एक अलग स्वाद है। अब, आप इन मिठाइयों को छोटे समूहों में विभाजित करना चाहते हैं, जहाँ प्रत्येक समूह में केवल एक प्रकार की मिठाई हो।

उदाहरण के लिए, मान लीजिए कि आपके पास 56 मिठाइयाँ हैं। आप इन्हें छोटे ढेरों में समूहित करना शुरू करते हैं:

• सबसे पहले, आप देखते हैं कि आप इन्हें प्रत्येक ढेर में 14 मिठाइयों के साथ विभाजित कर सकते हैं, और आपके पास 4 ढेर होंगे (14 × 4 = 56)।
• फिर, आप इनमें से एक ढेर (14 मिठाइयाँ) को 7 मिठाइयों और 2 मिठाइयों में विभाजित करते हैं (7 × 2 = 14)।
• अंत में, आप अन्य ढेर को देखते हैं जिसमें 4 मिठाइयाँ हैं और देखते हैं कि आप इसे दो समूहों में विभाजित कर सकते हैं, प्रत्येक में 2 मिठाइयाँ (2 × 2 = 4)।

अब, आपने मिठाइयों को जितना संभव हो सके विभाजित कर दिया है, तो आपके पास हैं:

• 2 मिठाइयों के दो ढेर
• 1 मिठाई का ढेर जिसमें 7 मिठाइयाँ हैं

ये संख्याएँ—2 और 7—प्रधान संख्याएँ हैं, जिसका अर्थ है कि इन्हें और छोटे समूहों में नहीं बाँटा जा सकता। इसलिए, 56 का प्रधान गुणनफल 2 × 2 × 2 × 7 है।

यह क्यों महत्वपूर्ण है? प्रधान गुणनफल किसी संख्या को उसके मूल निर्माण खंडों में तोड़ने की तरह है, ठीक वैसे ही जैसे मिठाइयों को समान स्वाद वाले समूहों में अलग करना। हर संख्या (1 से बड़ी) को इस तरह तोड़ा जा सकता है जब तक कि केवल प्रधान संख्याएँ न बचें। उदाहरण के लिए, यदि आप जानना चाहते हैं कि दो संख्याएँ, जैसे 56 और 63, सह-प्रधान हैं या नहीं (जिसका अर्थ है कि उनके पास 1 के अलावा कोई सामान्य गुणांक नहीं है), तो आप उनके प्रधान गुणनफलों को देख सकते हैं:

• 56 = 2 × 2 × 2 × 7
• 63 = 3 × 3 × 7

यहाँ, आप देख सकते हैं कि दोनों संख्याएँ प्रधान गुणांक 7 साझा करती हैं, इसलिए वे सह-प्रधान नहीं हैं। उनके पास कुछ समान है, जैसे कि यदि दो अलग-अलग मिठाई की थैलियों में एक ही स्वाद हो।

क्यों क्रम महत्वपूर्ण नहीं है

जब आप संख्याओं को एक साथ गुणा करते हैं ताकि मूल संख्या पर वापस जा सकें, तो आप जिस क्रम में उन्हें गुणा करते हैं, उससे परिणाम नहीं बदलता है।

उदाहरण के लिए:

• 2 × 3 × 5 = 30
• 5 × 2 × 3 = 30

आप इन्हें किसी भी क्रम में व्यवस्थित करें, समान संख्याओं को गुणा करने से हमेशा समान कुल मिलेगा। यह ऐसा है जैसे कहना कि आप चॉकलेट को किसी भी क्रम में उठाएं, अंत में आपके पास हमेशा समान संख्या में चॉकलेट होगी!

दो संख्याओं के उत्पाद का प्राथमिक गुणनखंड

जब हम किसी संख्या का प्राथमिक गुणनखंड खोजने की कोशिश करते हैं, तो हम इसे दो गुणकों के उत्पाद के रूप में लिखने से शुरू करते हैं। उदाहरण के लिए, हम 72 को 12 x 6 के रूप में व्यक्त कर सकते हैं।

एक उदाहरण के माध्यम से समझना

अब, आप प्रत्येक छोटे बैग पर एक नज़र डालते हैं:

• 12 चॉकलेट वाला बैग को 2, 2, और 3 चॉकलेट में और विभाजित किया जा सकता है (12 = 2 × 2 × 3)।
• 6 चॉकलेट वाला बैग 2 और 3 चॉकलेट में विभाजित किया जा सकता है (6 = 2 × 3)।

अब, बड़े बैग (जो 72 है) में मूल चॉकलेट के प्रकारों को जानने के लिए, आप बस दोनों छोटे बैग से चॉकलेट को जोड़ते हैं:

• 72 = 2 × 2 × 3 × 2 × 3

इसे आसान बनाने के लिए, आप उन्हें इस तरह व्यवस्थित कर सकते हैं:

• 72 = 2 × 2 × 2 × 3 × 3

अब, आपने पता लगा लिया है कि 72 चॉकलेट का बड़ा बैग 2 और 3 से बना है।

प्राइम फैक्टराइजेशन का उपयोग करके यह जांचना कि क्या दो संख्याएँ सह-प्राइम हैं

मान लीजिए आपके पास कैंडीज़ के दो अलग-अलग बैग हैं, एक में 56 कैंडीज़ हैं और दूसरे में 63 कैंडीज़ हैं। आप यह जांचना चाहते हैं कि क्या दोनों बैग में कोई सामान्य प्रकार की कैंडी है, जिसका अर्थ है कि वे सह-प्राइम नहीं हैं। आप दोनों बैग की कैंडीज़ का विश्लेषण करते हैं:

• 56-कैंडी बैग में 2 × 2 × 2 × 7 कैंडीज़ हैं।
• 63-कैंडी बैग में 3 × 3 × 7 कैंडीज़ हैं।

जब आप उनकी तुलना करते हैं, तो आप देखते हैं कि दोनों बैग में 7 कैंडीज़ हैं। चूंकि वे एक सामान्य प्रकार की कैंडी (जो कि 7 है) साझा करते हैं, इसलिए वे सह-प्राइम नहीं हैं। अब हम दो अन्य बैग के साथ प्रयास करते हैं, एक में 80 कैंडीज़ और दूसरे में 63 कैंडीज़:

• 80-कैंडी बैग में 2 × 2 × 2 × 2 × 5 कैंडीज़ हैं।
• 63-कैंडी बैग में 3 × 3 × 7 कैंडीज़ हैं।

इस बार, जब आप दोनों की तुलना करते हैं, तो आप देखते हैं कि उनके बीच कोई सामान्य प्रकार की कैंडी नहीं है। चूंकि वे कोई सामान्य गुणांक साझा नहीं करते हैं, ये दो संख्याएँ (80 और 63) सह-प्राइम हैं!

अधिक उदाहरण

उदाहरण 1: दो बैग पर विचार करें, एक में 40 कैंडीज़ और दूसरे में 231 कैंडीज़।

• 40-कैंडी बैग में 2 × 2 × 2 × 5 कैंडीज़ हैं।
• 231-कैंडी बैग में 3 × 7 × 11 कैंडीज़ हैं।
• दोनों बैग के बीच कोई सामान्य प्रकार की कैंडी नहीं है, इसलिए 40 और 231 सह-प्राइम हैं।

उदाहरण 2: दो अन्य बैग पर विचार करें, एक में 242 कैंडीज़ और दूसरे में 195 कैंडीज़।

• 242-कैंडी बैग में 2 × 11 × 11 कैंडीज़ हैं।
• 195-कैंडी बैग में 3 × 5 × 13 कैंडीज़ हैं।
• फिर से, कोई सामान्य प्रकार की कैंडी नहीं है, इसलिए 242 और 195 भी सह-प्राइम हैं।

प्राइम फैक्टराइजेशन का उपयोग करके यह जांचना कि क्या एक संख्या दूसरी से विभाजित है

उदाहरणों के साथ समझना संख्याओं को फलों से भरी टोकरी के रूप में सोचें, और प्रत्येक प्रकार का फल एक प्राइम फैक्टर का प्रतिनिधित्व करता है। अब, आप यह जांचना चाहते हैं कि क्या एक टोकरी (संख्या) पूरी तरह से दूसरी टोकरी में समा सकती है बिना कुछ बाहर छोड़े। यदि छोटी टोकरी के सभी फल (प्राइम फैक्टर्स) बड़ी टोकरी के अंदर समा जाते हैं, तो बड़ी संख्या छोटी संख्या से विभाज्य है।

उदाहरण 1: क्या 168, 12 से विभाज्य है? मान लीजिए कि आपके पास 168 फलों की एक टोकरी है और दूसरी टोकरी में 12 फल हैं। यह जांचने के लिए कि क्या 168, 12 से विभाज्य है, हम प्रत्येक टोकरी में फलों (प्राइम फैक्टर्स) को तोड़ते हैं।

• 168 = 2 × 2 × 2 × 3 × 7
• 12 = 2 × 2 × 3

अब, दोनों टोकरी में फलों पर ध्यान दें। आप देख सकते हैं कि 12 फल वाली टोकरी (2 × 2 × 3) के सभी फल 168 फल वाली टोकरी में भी हैं। इसका मतलब है कि आप 12 फल वाली टोकरी को 168 फल वाली टोकरी के अंदर बिना कुछ छोड़े रख सकते हैं। इसलिए, 168, 12 से विभाज्य है!

उदाहरण 2: क्या 75, 21 से विभाज्य है? अब, मान लीजिए कि आपके पास 75 फलों की एक टोकरी है और दूसरी टोकरी में 21 फल हैं।

• 75 = 3 × 5 × 5
• 21 = 3 × 7

जब हम फलों को देखते हैं, तो हम देखते हैं कि 75 फल वाली टोकरी में 3 और 5 हैं, लेकिन इसमें 7 नहीं है, जो 21 फल वाली टोकरी में है। इसका मतलब है कि छोटी टोकरी पूरी तरह से बड़ी टोकरी में नहीं समा सकती। इसलिए, 75, 21 से विभाज्य नहीं है।

विभाज्यता परीक्षण

विभाज्यता परीक्षण ऐसे शॉर्टकट होते हैं जो आपको यह पता लगाने में मदद करते हैं कि क्या एक संख्या को दूसरी संख्या से बिना लंबे विभाजन के विभाजित किया जा सकता है। पूरी प्रक्रिया को किए बिना, आप पैटर्न या नियमों का उपयोग करके जल्दी से जांच सकते हैं।

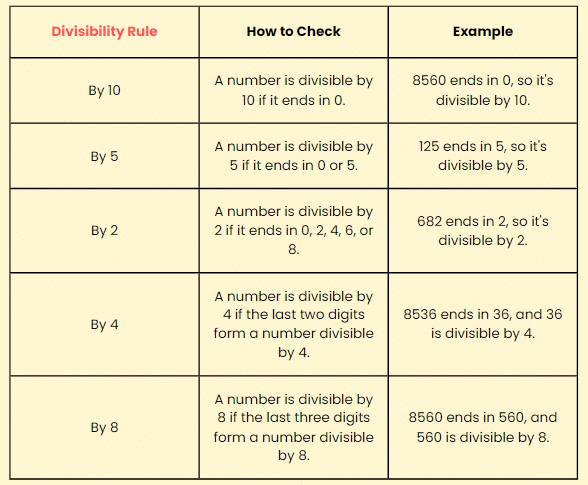
10 से विभाज्यता

• किसी संख्या की 10 से विभाज्यता की जांच करने के लिए, बस अंतिम अंक पर ध्यान दें। यदि अंतिम अंक 0 है, तो संख्या 10 से विभाज्य है।

उदाहरण: क्या 8560 10 से विभाज्य है?

• अंतिम अंक पर ध्यान दें: 0। चूंकि यह 0 पर समाप्त होता है, 8560 10 से विभाज्य है।

5 से विभाज्यता

• 5 से विभाज्यता के लिए, नियम समान है लेकिन थोड़ा अलग है। यदि अंतिम अंक 0 या 5 है, तो संख्या 5 से विभाज्य है।

उदाहरण: क्या 8560 5 से विभाज्य है?

• अंतिम अंक पर ध्यान दें: 0। चूंकि यह 0 पर समाप्त होता है, 8560 5 से विभाज्य है।

2 से विभाज्यता

• किसी संख्या की 2 से विभाज्यता तभी होती है जब उसका अंतिम अंक even (सम) हो। इसका मतलब है कि अंतिम अंक 0, 2, 4, 6, या 8 होना चाहिए।

उदाहरण: क्या 8560 2 से विभाज्य है?

• अंतिम अंक पर ध्यान दें: 0। चूंकि यह 0 (एक सम संख्या) पर समाप्त होता है, 8560 2 से विभाज्य है।

4 से विभाज्यता

• किसी संख्या की 4 से विभाज्यता की जांच करने के लिए, संख्या के अंतिम दो अंकों पर ध्यान दें। यदि इन दो अंकों से बनी संख्या 4 से विभाज्य है, तो पूरी संख्या 4 से विभाज्य है।

उदाहरण: क्या 8536 4 से विभाज्य है?

• अंतिम दो अंकों पर ध्यान दें: 36। चूंकि 36 ÷ 4 = 9 (कोई शेष नहीं), 8536 4 से विभाज्य है।

8 से विभाज्यता

• 8 से विभाज्यता के लिए, संख्या के अंतिम तीन अंकों की जांच करें। यदि इन तीन अंकों से बनी संख्या 8 से विभाज्य है, तो पूरी संख्या 8 से विभाज्य है।

उदाहरण: क्या 8560 8 से विभाज्य है?

संख्याओं के साथ मज़ा

विशेष संख्याएँ चलिए देखते हैं कि विभिन्न संख्याएँ दूसरों की तुलना में विशेष क्यों मानी जा सकती हैं। यहाँ संख्याओं का पहला सेट है: 9, 16, 25, 43। इन संख्याओं में से प्रत्येक को विशेष रूप से देखा जा सकता है, यह इस पर निर्भर करता है कि आप उन्हें कैसे देखते हैं:

• 9: यह विशेष है क्योंकि यह एकमात्र एकल-अंक संख्या है। यह एक पूर्ण वर्ग भी है (3 × 3)।
• 16: यह विशेष है क्योंकि यह समूह में एकमात्र सम संख्या है, और यह भी एक पूर्ण वर्ग है (4 × 4)।
• 25: यह विशेष है क्योंकि यह 5 का एकमात्र गुणांक है, और यह भी एक पूर्ण वर्ग है (5 × 5)।
• 43: यह विशेष है क्योंकि यह एकमात्र अभाज्य संख्या है, जिसका अर्थ है कि इसके पास 1 और स्वयं के अलावा कोई विभाजक नहीं है। इसके अलावा, यह इस सेट में एकमात्र संख्या है जो पूर्ण वर्ग नहीं है।

अब, चलिए यह पता लगाने की कोशिश करते हैं कि निम्नलिखित बक्सों में संख्याएँ विशेष क्यों हैं:

बॉक्स 1: 5, 7, 12, 35

• 5: यह एक अभाज्य संख्या है और यह एकमात्र संख्या है जो 5 पर समाप्त होती है।
• 7: यह भी एक अभाज्य संख्या है।
• 12: यह एकमात्र संख्या है जो 3 से विभाजित होती है (12 = 3 × 4)।
• 35: यह एकमात्र संख्या है जो 7 और 5 का गुणांक है।

बॉक्स 2: 3, 8, 11, 24

• 3: यह एकमात्र एकल-अंक अभाज्य संख्या है।
• 8: यह एकमात्र सम संख्या है जो 2 का घातांक भी है (2 × 2 × 2)।
• 11: यह एकमात्र दो-अंक की अभाज्य संख्या है।
• 24: यह एकमात्र संख्या है जो 8 का गुणांक है।

बॉक्स 3: 27, 3, 123, 31

• 27: यह एकमात्र संख्या है जो एक पूर्ण घन है (3 × 3 × 3)।
• 3: यह एकमात्र एकल अंकीय अभाज्य संख्या है।
• 123: यह एकमात्र तीन अंकीय संख्या है।
• 31: यह एक अभाज्य संख्या है।

बॉक्स 4: 17, 27, 44, 65

• 17: यह एक अभाज्य संख्या है।
• 27: यह एकमात्र संख्या है जो एक पूर्ण घन है (3 × 3 × 3)।
• 44: यह एकमात्र सम संख्या है।
• 65: यह एकमात्र संख्या है जो 5 का गुणनखंड है।

एक अभाज्य पहेली

इस पहेली में, लक्ष्य है कि एक ग्रिड को अभाज्य संख्याओं से भरा जाए ताकि प्रत्येक पंक्ति का गुणनफल दाईं ओर के संख्या के बराबर हो, और प्रत्येक कॉलम का गुणनफल उसके नीचे की संख्या के बराबर हो। यहाँ पहेली को हल करने का तरीका है:

पहेली ग्रिड:

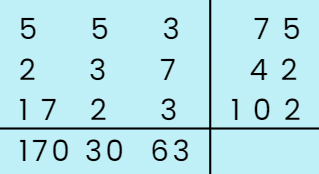
पहेली को हल करने के नियम:

• केवल अभाज्य संख्याएँ: प्रत्येक सेल में एक अभाज्य संख्या भरी जानी चाहिए।
• पंक्तियों का गुणनफल: प्रत्येक पंक्ति में संख्याओं का गुणनफल उस पंक्ति के दाईं ओर की संख्या के बराबर होना चाहिए।
• कॉलम का गुणनफल: प्रत्येक कॉलम में संख्याओं का गुणनफल उस कॉलम के नीचे की संख्या के बराबर होना चाहिए।

पहली पंक्ति में अभाज्य संख्याएँ 5, 5, और 3 हैं। गुणनफल है 5 × 5 × 3 = 75। पहली कॉलम में अभाज्य संख्याएँ 5, 2, और 17 हैं। गुणनफल है 5 × 2 × 17 = 170।

इन नियमों का पालन करके, आप अभाज्य पहेली को हल कर सकते हैं और सुनिश्चित कर सकते हैं कि सभी शर्तें पूरी हों!