NCERT समाधान: प्राइम टाइम | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

पृष्ठ 108

समस्या हल करें

प्रश्न 1: 'इडली-वड़ा' कितनी बार कहा गया है जब यह 10वीं बार कहा जाता है? उत्तर: 'इडली-वड़ा' का 10वां अवसर निर्धारित करने के लिए, हमें उन संख्याओं को पहचानना होगा जो 3 और 5 दोनों के गुणांक हैं। जिन संख्याओं के लिए 'इडली-वड़ा' कहा जाता है, वे 15 के गुणांक हैं। यह अनुक्रम है: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150,… इस प्रकार, खिलाड़ियों को 'इडली-वड़ा' कहने के लिए 10वीं संख्या 150 है। या 'इडली-वड़ा' के 10वीं बार कहे जाने वाली संख्या = 10 x 15 = 150।

प्रश्न 2: यदि खेल 1 से 90 तक की संख्याओं के लिए खेला जाता है, तो पता करें: (क) बच्चे 'इडली' कितनी बार कहेंगे (जिसमें वे 'इडली-वड़ा' कहते हैं)? उत्तर: 1 से 90 तक 3 के गुणांक हैं: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87 और 90। इस प्रकार, बच्चे 'इडली' 30 बार कहेंगे।

या 'इडली' उन संख्याओं के लिए कहा जाता है जो 3 के गुणांक हैं।

बच्चों द्वारा 'इडली' कहने की संख्या = 90 / 3

= 30 बार।

(ख) बच्चे 'वड़ा' कितनी बार कहेंगे (जिसमें वे 'इडली-वड़ा' कहते हैं)? उत्तर: 1 से 90 तक 5 के गुणांक हैं: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85 और 90। इस प्रकार, बच्चे 'वड़ा' 18 बार कहेंगे।

या 'वड़ा' उन संख्याओं के लिए कहा जाता है जो 5 के गुणांक हैं।

बच्चों द्वारा 'वड़ा' कहने की संख्या = 90 / 5

= 18 बार।

(ग) बच्चे 'इडली-वड़ा' कितनी बार कहेंगे? उत्तर: 15 के गुणांक हैं: 15, 30, 45, 60, 75 और 90। इस प्रकार, बच्चे 'इडली-वड़ा' 6 बार कहेंगे।

या 'इडली-वड़ा' उन संख्याओं के लिए कहा जाता है जो 15 के गुणांक हैं।

बच्चों द्वारा 'इडली- वडा' कहने की संख्या = 90 / 15

= 6 बार। प्रश्न 3: अगर खेल 900 तक खेला गया तो आपके उत्तर कैसे बदलेंगे? उत्तर: अगर खेल 900 तक खेला गया:

• 'इडली' कहने की बार (जिसमें 'इडली- वडा' शामिल हैं): 900/3 = 300 तीन के गुणांक हैं।
• 900 तक 15 के गुणांक हैं: 900/15 = 60
• कुल बार 'इडली' कहा गया: 300।
• 'वड़ा' कहने की बार (जिसमें 'इडली- वडा' शामिल हैं): 900/5 = 180 पांच के गुणांक हैं।
• 60 बार 'इडली- वडा' कहा गया।
• कुल बार 'वड़ा' कहा गया: 180।
• 'इडली- वडा' कहने की बार: 'इडली- वडा' 15 के गुणांक के लिए कहा जाता है, और 900/15 = 60 गुणांक हैं।
• कुल बार 'इडली- वडा' कहा गया: 60।

प्रश्न 4: क्या यह संख्या किसी तरह 'इडली- वडा' खेल से संबंधित है?

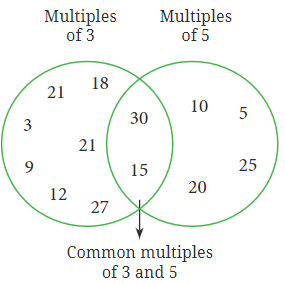
उत्तर: हाँ, यह 'इडली- वडा' खेल से संबंधित है, यदि हम 3 को इडली और 5 को वड़ा मानते हैं।

तीन के गुणांक: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60।

पांच के गुणांक: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60।

15 के गुणांक: 15, 30, 45, 60।

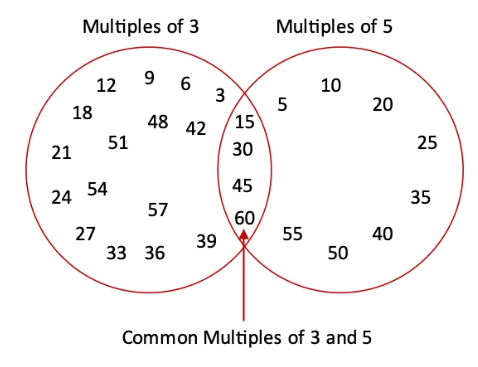
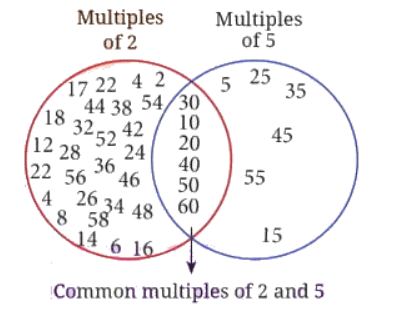
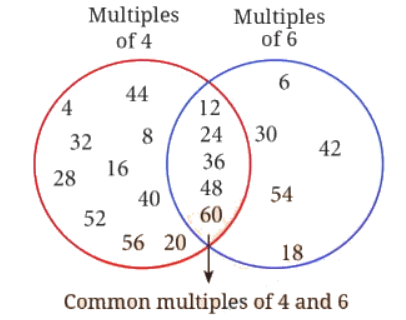
प्रश्न: अब हम 'इडली- वडा' खेलेंगे विभिन्न संख्या के जोड़ों के साथ: (क) 2 और 5, (ख) 3 और 7, (ग) 4 और 6। हम छोटे संख्या के गुणांक के लिए 'इडली' कहेंगे, बड़े संख्या के गुणांक के लिए 'वड़ा' और सामान्य गुणांक के लिए 'इडली- वडा' कहेंगे। यदि खेल 60 तक खेला जाए तो चित्र बनाएं जो चित्र 5.1 के समान हो। उत्तर: (क) 2 और 5

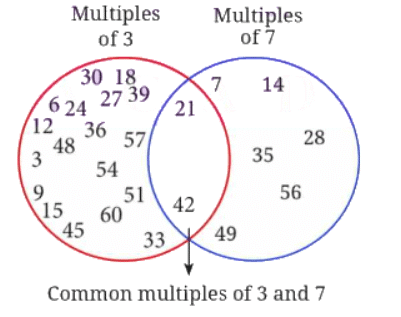
(ख) 3 और 7 (ग) 4 और 6

पृष्ठ 109

प्रश्न: निम्नलिखित में से कौन सा अन्य संख्या हो सकती है: 2, 3, 5, 8, 10? उत्तर: 2

पृष्ठ 110 और 111

प्रश्न: किस कूद के आकार के माध्यम से 15 और 30 दोनों पर पहुँचा जा सकता है? कई कूद के आकार संभव हैं। सभी का पता लगाने का प्रयास करें। उत्तर:

जंपिंग (Jumpy) को 15 और 30 दोनों पर पहुँचने के लिए, आपको इन दोनों संख्याओं के सामान्य गुणांक निर्धारित करने होंगे। यहाँ बताया गया है कि आप इन सामान्य कूद के आकारों को कैसे ढूंढ सकते हैं:

15 के गुणांक:

15 को इस प्रकार लिखा जा सकता है: 15 = 3 × 5

15 के गुणांक हैं: 1, 3, 5, 15

30 के गुणांक:

30 को इस प्रकार लिखा जा सकता है: 30 = 2 × 3 × 5

30 के गुणांक हैं: 1, 2, 3, 5, 6, 10, 15, 30

इन दोनों सूचियों के बीच के सामान्य गुणांक हैं: 1, 3, 5, 15। इसलिए, कूद के आकार जो जंपिंग को 15 और 30 दोनों पर पहुँचने में सक्षम बनाते हैं, वे हैं 15 और 30 के सामान्य गुणांक।

इसलिए, कूद के आकार जो जंपिंग को 15 और 30 दोनों पर पहुँचने में सक्षम बनाते हैं, वे हैं: 1, 3, 5, 15

प्रश्न: नीचे दी गई तालिका को देखें। आपको क्या नजर आता है? तालिका में, 1. क्या छायांकित संख्याओं में कुछ सामान्य है? 2. क्या चिह्नित संख्याओं में कुछ सामान्य है? 3. कौन सी संख्याएँ दोनों छायांकित और चिह्नित हैं? इन संख्याओं को क्या कहा जाता है? उत्तर:

1. तालिका में छायांकित संख्याएँ हैं: 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69। ये सभी 3 के गुणांक हैं। इसलिए, छायांकित बॉक्स में संख्याएँ 3 के गुणांक हैं।

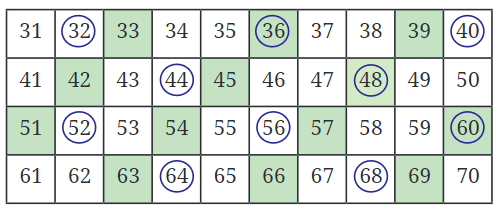
2. तालिका में चिह्नित संख्याएँ हैं: 32, 36, 40, 44, 48, 52, 56, 60, 64, 68। ये सभी 4 के गुणांक हैं। इसलिए, चिह्नित संख्याएँ 4 के गुणांक हैं।

3. जो संख्याएँ दोनों छायांकित और चिह्नित हैं, वे हैं: 36, 48, 60, 64। इन संख्याओं को 12 के सामान्य गुणांक कहा जाता है (3 और 4 दोनों)।

इसे समझें

Q1: 310 और 410 के बीच सभी 40 के गुणांक ज्ञात करें। उत्तर: 310 और 410 के बीच 40 के गुणांक हैं: 320, 360, 400।

व्याख्या: 310 से बड़े सबसे छोटे 40 के गुणांक को ढूंढें, जो कि 320 है। फिर, अगले गुणांक ज्ञात करने के लिए 40 जोड़ते रहें जब तक कि आप 410 तक न पहुँच जाएं या उसे पार न कर लें।

Q2: मैं कौन हूँ?

• (a) मैं 40 से कम एक संख्या हूँ। मेरे गुणांकों में से एक 7 है। मेरी अंकों का योग 8 है। उत्तर: 7, 14, 21, 28, 35, ये सभी 40 से कम 7 के गुणांक हैं। और 35 एक ऐसा संख्या है जिसका अंकों का योग 8 है, यानी 35 = (3 + 5) = 8। इसलिए, मैं 35 हूँ।
• 
• (b) मैं 100 से कम एक संख्या हूँ। मेरे दो गुणांक 3 और 5 हैं। मेरे एक अंक दूसरे से 1 अधिक है। उत्तर: 3 और 5 के सामान्य गुणांक 15, 30, 45, 60, 75, 90 हैं (जो 100 से कम हैं)। और एक संख्या है जिसमें एक अंक दूसरे से 1 अधिक है, वह है 45। इसलिए, मैं 45 हूँ।
• 

Q3: एक संख्या जिसके सभी गुणांकों का योग उस संख्या के दोगुने के बराबर होता है, उसे पूर्ण संख्या कहा जाता है। संख्या 28 एक पूर्ण संख्या है। इसके गुणांक हैं 1, 2, 4, 7, 14, और 28। उनका योग 56 है, जो 28 का दोगुना है। 1 और 10 के बीच एक पूर्ण संख्या ज्ञात करें। उत्तर: 1 और 10 के बीच पूर्ण संख्या 6 है। 6 के गुणांक हैं 1, 2, 3 और 6, और उनका योग 12 है, जो 6 का दोगुना है।

• 1 का गुणांक नहीं है। (1 पूर्ण संख्या नहीं है)
• 2 के गुणांक → 1, 2। गुणांकों का योग = 1 + 2 = 3। 3, 2 का दोगुना नहीं है। (2 पूर्ण संख्या नहीं है)
• 3 के गुणांक → 1, 3। गुणांकों का योग = 1 + 3 = 4। 4, 3 का दोगुना नहीं है। (3 पूर्ण संख्या नहीं है)
• 4 के गुणांक → 1, 2, 4। गुणांकों का योग = 1 + 2 + 4 = 7। 7, 4 का दोगुना नहीं है। (4 पूर्ण संख्या नहीं है)
• 5 के गुणांक → 1, 5। गुणांकों का योग = 1 + 5 = 6। 6, 5 का दोगुना नहीं है। (5 पूर्ण संख्या नहीं है)
• 6 के गुणांक → 1, 2, 3, 6। गुणांकों का योग = 1 + 2 + 3 + 6 = 12। 12, 6 का दोगुना है। (6 पूर्ण संख्या है)
• 7 के गुणांक → 1, 7। गुणांकों का योग = 1 + 7 = 8। 8, 7 का दोगुना नहीं है। (7 पूर्ण संख्या नहीं है)
• 8 के गुणांक → 1, 2, 4, 8। गुणांकों का योग = 1 + 2 + 4 + 8 = 15। 15, 8 का दोगुना नहीं है। (8 पूर्ण संख्या नहीं है)
• 9 के गुणांक → 1, 3, 9। गुणांकों का योग = 1 + 3 + 9 = 13। 13, 9 का दोगुना नहीं है। (9 पूर्ण संख्या नहीं है)
• 10 के गुणांक → 1, 2, 5, 10। गुणांकों का योग = 1 + 2 + 5 + 10 = 18। 18, 10 का दोगुना नहीं है। (10 पूर्ण संख्या नहीं है)

इसलिए, 6 1 और 10 के बीच एक पूर्ण संख्या है।

प्रश्न 4: निम्नलिखित संख्याओं के सामान्य गुणांक ज्ञात कीजिए:

• (क) 20 और 28
  • उत्तर: 20 और 28 के सामान्य गुणांक हैं 1, 2 और 4।

  व्याख्या: 20 के गुणांक हैं 1, 2, 4, 5, 10, और 20। 28 के गुणांक हैं 1, 2, 4, 7, 14, और 28। सामान्य गुणांक हैं 1, 2, और 4।

• (ख) 35 और 50
  • उत्तर: 35 और 50 के सामान्य गुणांक हैं 1 और 5।

  व्याख्या: 35 के गुणांक हैं 1, 5, 7, और 35। 50 के गुणांक हैं 1, 2, 5, 10, 25, और 50। सामान्य गुणांक हैं 1 और 5।

• (ग) 4, 8, और 12
  • उत्तर: 4, 8, और 12 के सामान्य गुणांक हैं 1 और 2, 4।

  व्याख्या: 4 के गुणांक हैं 1, 2, और 4। 8 के गुणांक हैं 1, 2, 4, और 8। 12 के गुणांक हैं 1, 2, 3, 4, 6, और 12। सामान्य गुणांक हैं 1 और 2, 4।

• (घ) 5, 15, और 25
  • उत्तर: 5, 15, और 25 का सामान्य गुणांक है 1 और 5।

  व्याख्या: 5 के गुणांक हैं 1 और 5। 15 के गुणांक हैं 1, 3, 5, और 15। 25 के गुणांक हैं 1, 5, और 25। सामान्य गुणांक है 5।

प्रश्न 5: ऐसे तीन संख्याएँ ज्ञात कीजिए जो 25 के गुणांक हों लेकिन 50 के गुणांक न हों।

उत्तर: 25, 75 और 125, ये तीन संख्याएँ 25 के गुणांक हैं लेकिन 50 के गुणांक नहीं हैं।

प्रश्न 6: अंशु और उसके दोस्त 'इडली-वड़ा' खेलते हैं, जिसमें दो संख्या होती हैं, जो दोनों 10 से छोटी हैं। जब पहली बार कोई 'इडली-वड़ा' कहता है, तो वह संख्या 50 के बाद होती है। 'इडली' और 'वड़ा' के लिए दो संख्याएँ क्या हो सकती हैं?

उत्तर: दो संख्याएँ 6 और 9 हो सकती हैं।

व्याख्या: यदि पहली बार "इडली-वड़ा" संख्या 50 के बाद कहते हैं और दोनों संख्याएँ 10 से छोटी हैं, तो हमें ऐसी दो संख्याएँ ज्ञात करनी हैं जिनका न्यूनतम सामान्य गुणांक 50 से थोड़ा अधिक हो। 6 और 9 का न्यूनतम सामान्य गुणांक 54 है, इसलिए ये दो संख्याएँ 6 और 9 हो सकती हैं। इसका अर्थ है कि पहली बार जब वे "इडली-वड़ा" कहेंगे, वह 54 पर होगा, क्योंकि 54 6 और 9 दोनों का गुणांक है।

प्रश्न 7: खजाना खोजने के खेल में, ग्रम्पी ने 28 और 70 पर खजाने रखे हैं। कौन से कूदने के आकार दोनों संख्याओं पर पहुँचेंगे? उत्तर:

28 के गुणांक: 1, 2, 4, 7, 14, 28। (ये कूदने के आकार 28 पर पहुँचेंगे)

70 के गुणांक: 1, 2, 5, 7, 10, 14, 35, 70। (ये कूदने के आकार 70 पर पहुँचेंगे)

सामान्य गुणांक: 1, 2, 7, 14।

इसलिए, 1, 2, 7 और 14 के कूदने के आकार दोनों संख्याओं 28 और 70 पर पहुँचेंगे।

प्रश्न 8: नीचे दिए गए चित्र में, गुणा ने सभी संख्याओं को मिटा दिया है सिवाय सामान्य गुणा के। उन संख्याओं को खोजें और खाली क्षेत्रों में गायब संख्याओं को भरें। उत्तर: सामान्य गुणा— बायाँ वृत्त (12 के गुणा): 12, 24, 36, 48, 60, 72, आदि। दायाँ वृत्त (8 के गुणा): 8, 16, 24, 32, 40, 48, 56, 64, 72, आदि। इसलिए, लाल वृत्त में 12 के गुणा हैं और नीले वृत्त में 8 के गुणा हैं।

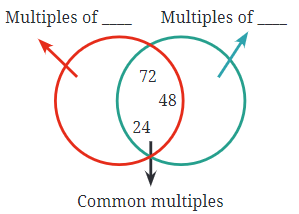
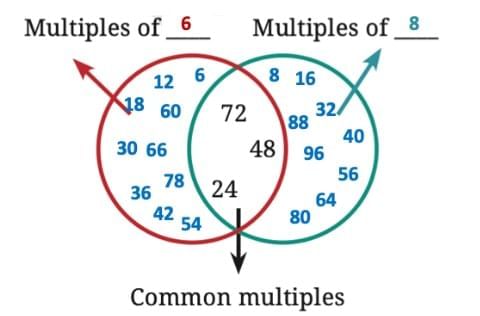
व्याख्या: वैन आरेख में, ओवरलैप (सामान्य गुणा) में संख्याएँ 24, 48, और 72 हैं। इसलिए, लाल वृत्त 24 के गुणा को दर्शा सकता है, और नीला वृत्त 48 के गुणा को दर्शा सकता है।

प्रश्न 9: 1 से 10 तक सभी संख्याओं का गुणा क्या है, सिवाय 7 के? उत्तर: 1 से 10 तक सभी संख्याओं का गुणा खोजने के लिए (7 को छोड़कर), हम 1, 2, 3, 4, 5, 6, 8, 9 और 10 का सबसे छोटा सामान्य गुणा निकालते हैं। इन संख्याओं का सबसे छोटा सामान्य गुणा 360 है। = 2 x 2 x 2 x 3 x 3 x 5 = 360।

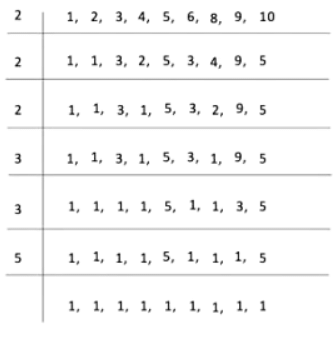
प्रश्न 10: 1 से 10 तक सभी संख्याओं का गुणा क्या है? उत्तर: 1 से 10 तक सभी संख्याओं का गुणा खोजने के लिए, हम 1, 2, 3, 4, 5, 6, 7, 8, 9 और 10 का सबसे छोटा गुणा निकालते हैं। इन संख्याओं का सबसे छोटा गुणा 2520 है। आवश्यक सबसे छोटा संख्या = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 के संख्याओं का L.C.M। = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 360 x 7 = 2520।

पृष्ठ 113

प्रश्न: 21 से 30 के बीच कितने अभाज्य (prime) संख्याएँ हैं? 21 से 30 के बीच कितनी संख्याएँ समुच्चय (composite) हैं? उत्तर: अभाज्य संख्याएँ वे संख्याएँ हैं जिनके केवल दो भाजक होते हैं: 1 और स्वयं संख्या। 21 से 30 के बीच अभाज्य संख्याएँ हैं: 23 और 29। इसलिए, वहाँ 2 अभाज्य संख्याएँ हैं। समुच्चय संख्याएँ वे होती हैं जिनके दो से अधिक भाजक होते हैं। 21 से 30 के बीच समुच्चय संख्याएँ हैं: 22, 24, 25, 26, 27, 28 और 30। इसलिए, वहाँ 7 समुच्चय संख्याएँ हैं।

पृष्ठ 114

प्रश्न 1: हम देखते हैं कि 2 एक अभाज्य और एक सम संख्या है। क्या कोई अन्य सम अभाज्य संख्या है?

उत्तर: नहीं, कोई अन्य सम अभाज्य संख्या नहीं है।

व्याख्या: संख्या 2 एकमात्र सम अभाज्य संख्या है क्योंकि एक अभाज्य संख्या के पास केवल दो अलग सकारात्मक भाजक होते हैं: 1 और स्वयं। कोई अन्य सम संख्या 2 से विभाजित हो सकती है, जिसका अर्थ है कि इसके पास कम से कम तीन भाजक होते हैं (1, 2, और स्वयं संख्या), इसलिए यह अभाज्य नहीं हो सकती।

प्रश्न 2: 100 तक की अभाज्य संख्याओं की सूची देखें। दो लगातार अभाज्य संख्याओं के बीच का सबसे छोटा अंतर क्या है? सबसे बड़ा अंतर क्या है? उत्तर: 100 तक की दो लगातार अभाज्य संख्याओं के बीच का सबसे छोटा अंतर जानने के लिए, चलिए उस सीमा में अभाज्य संख्याओं को सूचीबद्ध करते हैं और प्रत्येक जोड़ी के बीच के अंतर की गणना करते हैं: 100 तक की अभाज्य संख्याएँ: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97। लगातार अभाज्य संख्याओं के बीच के अंतर:

• 3 – 2 = 1
• 5 – 3 = 2
• 7 – 5 = 2
• 11 – 7 = 4
• 13 – 11 = 2
• 17 – 13 = 4
• 19 – 17 = 2
• 23 – 19 = 4
• 29 – 23 = 6
• 31 – 29 = 2
• 37 – 31 = 6
• 41 – 37 = 4
• 43 – 41 = 2
• 47 – 43 = 4
• 53 – 47 = 6
• 59 – 53 = 6
• 61 – 59 = 2
• 67 – 61 = 6
• 71 – 67 = 4
• 73 – 71 = 2
• 79 – 73 = 6
• 83 – 79 = 4
• 89 – 83 = 6
• 97 – 89 = 8

100 तक की दो लगातार अभाज्य संख्याओं के बीच का सबसे छोटा अंतर 1 है (अभाज्य संख्याओं 2 और 3 के बीच)। 100 तक की दो लगातार अभाज्य संख्याओं के बीच का सबसे बड़ा अंतर 8 है, जो अभाज्य संख्याओं 89 और 97 के बीच होता है।

प्रश्न 3: क्या पिछले पृष्ठ पर तालिका में प्रत्येक पंक्ति में अभाज्य संख्याओं की संख्या समान है? कौन सी दशकों में सबसे कम अभाज्य संख्याएँ हैं? कौन सी दशकों में सबसे अधिक अभाज्य संख्याएँ हैं? उत्तर: हर पंक्ति में अभाज्य संख्याओं की संख्या समान नहीं है। पंक्तियों के बीच अभाज्य संख्याओं की संख्या भिन्न होती है। दशक 90-99 में केवल 1 अभाज्य संख्या है (97), जिससे यह सबसे कम है। दशक 0-9 और 10-19 में सबसे अधिक अभाज्य संख्याएँ हैं, प्रत्येक में 4 अभाज्य संख्याएँ।

प्रश्न 4: निम्नलिखित में से कौन सी संख्याएँ अभाज्य हैं? 23, 51, 37, 26 उत्तर: 23 के भाजक: 1, 23।

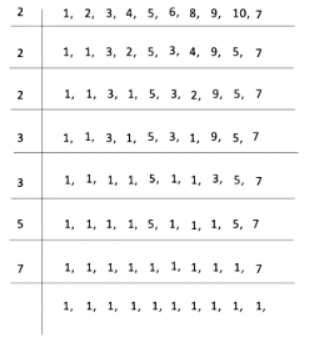
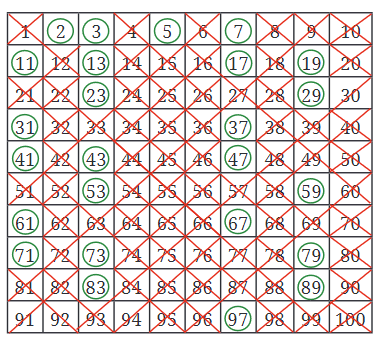
51 के गुणांक: 1, 3, 17, 51।

37 के गुणांक: 1, 37।

26 के गुणांक: 1, 2, 13, 26।

इसलिए, 23 और 37 अभाज्य हैं।

प्रश्न 5: 20 से कम के तीन अभाज्य संख्याओं के जोड़े लिखें, जिनका योग 5 का गुणांक हो।

उत्तर: 20 से कम की अभाज्य संख्याएँ: 2, 3, 5, 7, 11, 13, 17, 19।

• 2 + 3 = 5 (5 का गुणांक)
• 3 + 7 = 10 (5 का गुणांक)
• 7 + 13 = 20 (5 का गुणांक)

इसलिए, आवश्यक तीन अभाज्य संख्या के जोड़े हैं (2, 3); (3, 7) और (7, 13)।

प्रश्न 6: संख्याएँ 13 और 31 अभाज्य संख्याएँ हैं। इन दोनों संख्याओं के अंक 1 और 3 हैं। 100 तक ऐसे अभाज्य संख्या के जोड़े खोजें।

उत्तर: अंक 1 और 3 वाली संख्याएँ: 13, 31

• अंक 1 और 7 वाली संख्याएँ: (17, 71)
• अंक 3 और 7 वाली संख्याएँ: (37, 73)

इसलिए, आवश्यक अभाज्य जोड़े हैं (13, 31); (17, 71) और (37, 73)।

प्रश्न 7: 1 से 100 के बीच सात लगातार यौगिक संख्याएँ खोजें।

उत्तर: 1 से 100 के बीच सात लगातार यौगिक संख्याएँ हैं: 90, 91, 92, 93, 94, 95, और 96।

व्याख्या: एक यौगिक संख्या के दो से अधिक गुणांक होते हैं। संख्याएँ 90 से 96 सभी यौगिक हैं और क्रमशः आती हैं।

प्रश्न 8: जुड़वाँ अभाज्य ऐसे अभाज्य संख्याओं के जोड़े हैं जिनमें अंतर 2 होता है। उदाहरण के लिए, 3 और 5 जुड़वाँ अभाज्य हैं। 17 और 19 भी हैं। 1 से 100 के बीच अन्य जुड़वाँ अभाज्य खोजें।

उत्तर: 1 से 100 के बीच जुड़वाँ अभाज्य हैं: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), और (71, 73)।

व्याख्या: जुड़वाँ अभाज्य ऐसे अभाज्य संख्याओं के जोड़े होते हैं जिनका अंतर ठीक 2 होता है, और ये सभी जोड़े 1 से 100 के बीच हैं।

पृष्ठ 115

प्रश्न 9: पहचानें कि प्रत्येक कथन सत्य है या गलत। व्याख्या करें।

(a) कोई भी ऐसा प्राथमिक संख्या नहीं है जिसका इकाई अंक 4 है। उत्तर: सत्य।

व्याख्या: एक प्राथमिक संख्या को 1, 3, 7, या 9 में समाप्त होना चाहिए (संख्या 2 को छोड़कर) क्योंकि कोई भी संख्या जो 0, 2, 4, 6, या 8 में समाप्त होती है, वह 2 से विभाज्य होती है।

(b) प्राथमिक संख्याओं का गुणनफल भी प्राथमिक हो सकता है। उत्तर: असत्य।

व्याख्या: दो या अधिक प्राथमिक संख्याओं का गुणनफल एक संयुक्त संख्या बनाता है, न कि एक प्राथमिक।

(c) प्राथमिक संख्याओं के कोई गुणांक नहीं होते। उत्तर: असत्य।

व्याख्या: प्राथमिक संख्याओं के ठीक दो गुणांक होते हैं: 1 और स्वयं संख्या।

(d) सभी सम संख्याएँ संयुक्त संख्याएँ होती हैं। उत्तर: असत्य।

व्याख्या: संख्या 2 एक सम संख्या है, लेकिन यह एक प्राथमिक संख्या भी है।

(e) 2 एक प्राथमिक है और अगली संख्या 3 भी है। प्रत्येक अन्य प्राथमिक के लिए, अगली संख्या संयुक्त है। उत्तर: सत्य।

व्याख्या: 2 और 3 के बाद, किसी भी प्राथमिक के बाद अगली संख्या संयुक्त होती है क्योंकि यह कम से कम दो संख्याओं (1 और स्वयं प्राथमिक) से विभाज्य होती है।

प्रश्न 10: निम्नलिखित में से कौन सी संख्या ठीक तीन भिन्न प्राथमिक संख्याओं का गुणनफल है: 45, 60, 91, 105, 330? उत्तर: संख्या 105 ठीक तीन भिन्न प्राथमिक संख्याओं का गुणनफल है अर्थात् 3 × 5 × 7।

• 60 = 2 × 3 × 5 (तीन भिन्न प्राथमिक)
• 105 = 3 × 5 × 7 (तीन भिन्न प्राथमिक)
• 330 = 2 × 3 × 5 × 11 (चार भिन्न प्राथमिक, इसलिए यह गिनती में नहीं आता)
• 91 = 7 × 13 (दो भिन्न प्राथमिक)
• 45 = 3 × 3 × 5 (दो भिन्न प्राथमिक)

प्रश्न 11: आप 2, 4, और 5 का उपयोग करके एक बार में कितनी तीन-अंकीय प्राथमिक संख्याएँ बना सकते हैं? उत्तर: अंकों 2, 4 और 5 का एक बार उपयोग करके बनी संख्याएँ: 245, 254, 425, 452, 524, 542। 245 (5 से विभाज्य) — प्राथमिक नहीं 254 (2 से विभाज्य) — प्राथमिक नहीं 425 (5 से विभाज्य) — प्राथमिक नहीं 452 (2 से विभाज्य) — प्राथमिक नहीं 524 (2 से विभाज्य) — प्राथमिक नहीं 542 (2 से विभाज्य) — प्राथमिक नहीं। इसलिए, 2, 4 और 5 का उपयोग करके एक बार में कोई तीन-अंकीय प्राथमिक संख्या नहीं बनाई जा सकती।

प्रश्न 12: अवलोकन करें कि 3 एक प्राथमिक संख्या है, और 2 × 3 + 1 = 7 भी एक प्राथमिक है। क्या अन्य प्राथमिक संख्याएँ हैं जिनके लिए डबल करने और 1 जोड़ने पर एक अन्य प्राथमिक संख्या मिलती है? ऐसी कम से कम पांच उदाहरण खोजें। उत्तर: उन पांच प्राथमिक संख्याओं के लिए जिनके लिए डबल करने और 1 जोड़ने पर एक अन्य प्राथमिक संख्या मिलती है:

2 (क्योंकि 2 × 2 + 1 = 5)

• 2 (क्योंकि 2 × 2 + 1 = 5)
• 3 (क्योंकि 2 × 3 + 1 = 7)
• 5 (क्योंकि 2 × 5 + 1 = 11)
• 11 (क्योंकि 2 × 11 + 1 = 23)
• 23 (क्योंकि 2 × 23 + 1 = 47)

प्रश्न: ग्रम्पी को खजाने को कहाँ रखना चाहिए ताकि जंपिंग दोनों खजानों तक न पहुँच सके?

उत्तर: जंपिंग को दोनों खजानों तक पहुँचने से रोकने के लिए, ग्रम्पी को खजाने को उन दो संख्याओं पर रखना चाहिए जो किसी भी सामान्य गुणांक (1 को छोड़कर) को साझा नहीं करती हैं। इन संख्याओं को को-प्राइम कहा जाता है। उदाहरण के लिए: ग्रम्पी खजाने को 4 और 9 पर रख सकता है, क्योंकि वे को-प्राइम हैं (इनके पास 1 को छोड़कर कोई सामान्य गुणांक नहीं है)। इसका मतलब है कि जंपिंग एकल कूद के आकार के साथ दोनों संख्याओं तक नहीं पहुँच सकता, सिवाय कूद के आकार 1 के, जो खेल के नियमों द्वारा अनुमत नहीं है। यह रणनीति सुनिश्चित करती है कि जंपिंग 1 के अलावा किसी अन्य कूद के आकार का उपयोग करके दोनों संख्याओं पर नहीं पहुँच सकेगा।

पृष्ठ 116

प्रश्न: निम्नलिखित संख्याओं के जोड़े में से कौन सी को-प्राइम हैं?

(a) 18 और 35

उत्तर: यहाँ 18 के गुणांक = 1 × 2 × 3 × 3 और 35 के गुणांक = 1 × 5 × 7 हैं। 1 को छोड़कर कोई सामान्य गुणांक नहीं है। इसलिए 18 और 35 को-प्राइम संख्याएँ हैं।

(b) 15 और 37

उत्तर: 15 के गुणांक = 1 × 3 × 5 और 37 के गुणांक = 1 × 37 हैं। 1 को छोड़कर कोई सामान्य गुणांक नहीं है। इसलिए 15 और 37 को-प्राइम संख्याएँ हैं।

(c) 30 और 415

उत्तर: दिए गए संख्याएँ 30 और 415 हैं। यहाँ 30 के गुणांक = 1 × 2 × 3 × 5 और 415 के गुणांक = 5 × 83 हैं। स्पष्ट रूप से 5, 30 और 415 का सामान्य गुणांक है। इसलिए 30 और 415 को-प्राइम संख्याएँ नहीं हैं।

(d) 17 और 69 उत्तर: 17 के गुणनखंड: 1, 17 सामान्य गुणनखंड: 1 सह-प्राइम: हाँ और 69 के गुणनखंड: 1, 3, 23, 69

(e) 81 और 18 उत्तर: 81 के गुणनखंड: 1, 3, 9, 27, 81 और 18 के गुणनखंड: 1, 2, 3, 6, 9, 18 सामान्य गुणनखंड: 1, 3, 9 सह-प्राइम: नहीं (इनमें 3 और 9 का सामान्य गुणनखंड है) अंतिम परिणाम:

• 18 और 35: सह-प्राइम
• 15 और 37: सह-प्राइम
• 30 और 415: सह-प्राइम नहीं
• 17 और 69: सह-प्राइम
• 81 और 18: सह-प्राइम नहीं

प्रश्न: 'इडली-वड़ा' खेल खेलते समय, अंकुश ने कुछ दिलचस्प चीजें देखीं! (a) कभी-कभी पहला सामान्य गुणनफल दो संख्याओं के गुणनफल के समान होता था। (b) अन्य समय में, पहला सामान्य गुणनफल दो संख्याओं के गुणनफल से कम होता था। प्रत्येक के लिए उदाहरण खोजें। यह सह-प्राइम संख्या के जोड़े से कैसे संबंधित है?

उत्तर: (a) कभी-कभी पहला सामान्य गुणनफल दो संख्याओं के गुणनफल के समान होता है। यह तब होता है जब दोनों संख्याएँ सह-प्राइम होती हैं, अर्थात् उनके पास 1 के अलावा कोई सामान्य गुणनखंड नहीं होता। उदाहरण के लिए: 3 और 5 का जोड़ा लें। 3 और 5 का गुणनफल 3 × 5 = 15 है। 3 और 5 का न्यूनतम सामान्य गुणनफल (LCM) भी 15 है। चूंकि 3 और 5 सह-प्राइम हैं, इसलिए उनका LCM उनके गुणनफल के समान है।

(b) दो संख्याओं का गुणनफल से कम पहला सामान्य गुणनफल: यह तब होता है जब दोनों संख्याएँ सह-प्राइम नहीं होती (वे 1 से बड़ा एक सामान्य गुणनखंड साझा करती हैं)। ऐसे मामलों में, LCM दो संख्याओं के गुणनफल से कम होता है। उदाहरण के लिए: 4 और 6 का जोड़ा लें। 4 और 6 का गुणनफल 4 × 6 = 24 है। 4 और 6 का LCM 12 है (24 नहीं) क्योंकि वे एक सामान्य गुणनखंड (2) साझा करते हैं। चूंकि 4 और 6 सह-प्राइम नहीं हैं, LCM उनके गुणनफल से कम है।

सह-प्राइम संख्याओं से संबंध:

सह-प्रधान संख्याएँ: जब दो संख्याएँ सह-प्रधान होती हैं (जैसे 3 और 5), तो उनका LCM (कम से कम गुणज) उन दोनों संख्याओं का गुणनफल होता है क्योंकि उनके बीच कोई सामान्य गुणांक नहीं होता।

• सह-प्रधान संख्याएँ: जब दो संख्याएँ सह-प्रधान होती हैं (जैसे 3 और 5), तो उनका LCM उन दोनों संख्याओं का गुणनफल होता है क्योंकि उनके बीच कोई सामान्य गुणांक नहीं होता।
• गैर सह-प्रधान संख्याएँ: जब दो संख्याएँ गैर सह-प्रधान होती हैं (जैसे 4 और 6), तो उनका LCM उनके गुणनफल से कम होता है क्योंकि सामान्य गुणांक एक छोटा गुणज बनाने की अनुमति देता है। इसलिए, यदि संख्याएँ सह-प्रधान हैं, तो उनका LCM उनके गुणनफल के बराबर होता है। यदि वे गैर सह-प्रधान हैं, तो उनका LCM उनके गुणनफल से कम होता है।

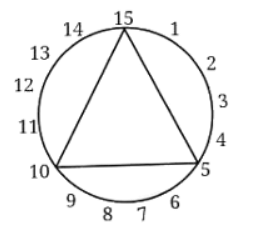
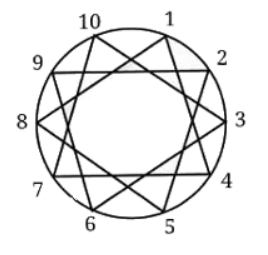
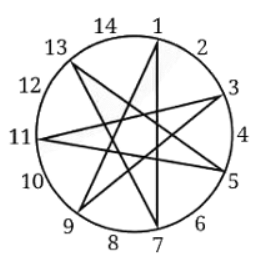
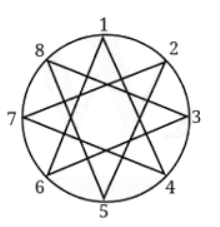
प्रश्न: निम्नलिखित धागा कला को देखें। पहले आरेख में 12 पेग हैं और धागा हर चौथे पेग से बंधा है (हम कहते हैं कि धागा-गैप 4 है)। दूसरे आरेख में 13 पेग हैं और धागा-गैप 3 है। अन्य आरेखों के बारे में क्या? इन चित्रों का अवलोकन करें, अपने निष्कर्षों को साझा करें और कक्षा में चर्चा करें।

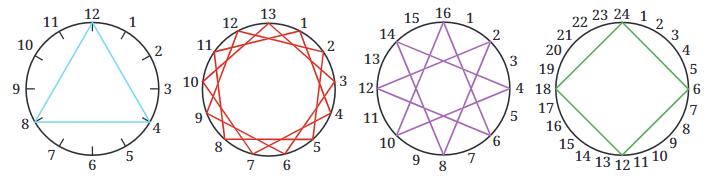
कुछ आरेखों में, धागा हर पेग से बंधा है। कुछ में, यह बंधा नहीं है। क्या यह दो संख्याओं (पेग की संख्या और धागा-गैप) के सह-प्रधान होने से संबंधित है? (a) 15 पेग, धागा-गैप 10 (b) 10 पेग, धागा-गैप 7 (c) 14 पेग, धागा-गैप 6 (d) 8 पेग, धागा-गैप 3

उत्तर: तीसरा आरेख: 16 पेग और धागा-गैप 6। चौथा आरेख: 24 पेग और धागा-गैप 6। (a) 15 पेग, धागा-गैप 10: (b) 10 पेग, धागा-गैप 7:

प्रश्न 1: निम्नलिखित संख्याओं के प्राथमिक गुणनखंड ज्ञात कीजिए: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000। उत्तर:

• (i) 64 का प्राथमिक गुणनखंड है 2 × 2 × 2 × 2 × 2 × 2।
• (ii) 104 का प्राथमिक गुणनखंड है 2 × 2 × 2 × 13।
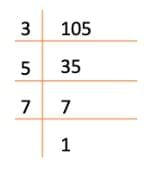
• (iii) 105 का प्राथमिक गुणनखंड है 3 × 5 × 7।
• (iv) 243 का प्राथमिक गुणनखंड है 3 × 3 × 3 × 3 × 3।
• (v) 320 का प्राथमिक गुणनखंड है 2 × 2 × 2 × 2 × 2 × 2 × 5।
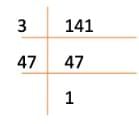
• (vi) 141 का प्राथमिक गुणनखंड है 3 × 47।
• (vii) 1728 का प्राथमिक गुणनखंड है 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3।
• (viii) 729 का प्राथमिक गुणनखंड है 3 × 3 × 3 × 3 × 3 × 3।
• (ix) 1024 का प्राथमिक गुणनखंड है 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2।
• (x) 1331 का प्राथमिक गुणनखंड है 11 × 11 × 11।
• (xi) 1000 का प्राथमिक गुणनखंड है 2 × 2 × 2 × 5 × 5 × 5।

प्रश्न 2: एक संख्या के प्राथमिक गुणनखंड में एक 2, दो 3, और एक 11 है। वह संख्या क्या है? उत्तर: वह संख्या 198 है।

व्याख्या: संख्या की गणना इस प्रकार की गई है: 2 × 3 × 3 × 11 = 198।

प्रश्न 3: तीन प्राथमिक संख्याएँ ज्ञात कीजिए, जो सभी 30 से कम हैं और जिनका गुणनफल 1955 है। उत्तर: 1955 का प्राथमिक गुणनखंड है: 1955 = 5 × 17 × 23। सभी गुणांक प्राथमिक संख्याएँ हैं और 30 से कम हैं। इसलिए, तीन प्राथमिक संख्याएँ जिनका गुणनफल 1955 है, वे हैं 5, 17, और 23।

प्रश्न 4: इन संख्याओं के प्राथमिक गुणनखंड ज्ञात कीजिए बिना पहले गुणा किए: (क) 56 × 25। उत्तर: 56 के प्राथमिक गुणनखंड हैं 2 × 2 × 2 × 7। 25 के प्राथमिक गुणनखंड हैं 5 × 5। 56 × 25 का संयुक्त प्राथमिक गुणनखंड है 2 × 2 × 2 × 7 × 5 × 5।

(b) 108 × 75 उत्तर: 108 के प्रमुख गुणांक = 2 × 2 × 3 × 3 × 3
75 के प्रमुख गुणांक = 3 × 5 × 5
108 × 75 का संयुक्त प्रमुख गुणनखंडन = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5

(c) 1000 × 81 उत्तर: 1000 के प्रमुख गुणांक = 2 × 2 × 2 × 5 × 5 × 5
81 के प्रमुख गुणांक = 3 × 3 × 3 × 3
1000 × 81 का संयुक्त प्रमुख गुणनखंडन = 2 × 2 × 2 × 5 × 5 × 5 × 3 × 3 × 3 × 3

प्रश्न 5: सबसे छोटा संख्या क्या है जिसका प्रमुख गुणनखंडन में है:
(a) तीन अलग-अलग प्रमुख संख्याएँ? उत्तर: सबसे छोटी प्रमुख संख्याएँ 2, 3, और 5 हैं। इन प्रमुख संख्याओं को गुणा करने पर सबसे छोटी संख्या मिलती है: 2 × 3 × 5 = 30
तो, सबसे छोटी संख्या जिसका प्रमुख गुणनखंडन में तीन अलग-अलग प्रमुख संख्याएँ हैं, वह 30 है।

(b) चार अलग-अलग प्रमुख संख्याएँ? उत्तर: सबसे छोटी चार प्रमुख संख्याएँ 2, 3, 5, और 7 हैं। इन प्रमुख संख्याओं को गुणा करने पर सबसे छोटी संख्या मिलती है: 2 × 3 × 5 × 7 = 210
इसलिए, सबसे छोटी संख्या जिसका प्रमुख गुणनखंडन में चार अलग-अलग प्रमुख संख्याएँ हैं, वह 210 है।

पृष्ठ 122

प्रश्न 1: क्या निम्नलिखित संख्याओं के जोड़े सह-प्रमुख हैं? पहले अनुमान लगाएँ और फिर प्रमुख गुणनखंडन का उपयोग करके अपने उत्तर की पुष्टि करें।

(a) 30 और 45 उत्तर: नहीं, 30 और 45 सह-प्रमुख नहीं हैं।
व्याख्या: 30 का प्रमुख गुणनखंडन 2 × 3 × 5 है, और 45 का प्रमुख गुणनखंडन 3 × 3 × 5 है। उनके पास सामान्य प्रमुख गुणांक (3 और 5) हैं, इसलिए वे सह-प्रमुख नहीं हैं।

(b) 57 और 85 उत्तर: हाँ, 57 और 85 सह-प्रमुख हैं।
व्याख्या: 57 का प्रमुख गुणनखंडन 3 × 19 है, और 85 का प्रमुख गुणनखंडन 5 × 17 है। उनके पास कोई सामान्य प्रमुख गुणांक नहीं हैं, इसलिए वे सह-प्रमुख हैं।

(c) 121 और 1331 उत्तर: नहीं, 121 और 1331 सह-प्रधान नहीं हैं।

व्याख्या: 121 का प्रधान गुणनखंड 11 × 11 है, और 1331 का प्रधान गुणनखंड 11 × 11 × 11 है। उनके पास सामान्य प्रधान गुणांक 11 है, इसलिए वे सह-प्रधान नहीं हैं।

(d) 343 और 216 उत्तर: हाँ, 343 और 216 सह-प्रधान हैं।

व्याख्या: 343 का प्रधान गुणनखंड 7 × 7 × 7 है, और 216 का प्रधान गुणनखंड 2 × 2 × 2 × 3 × 3 × 3 है। उनके पास कोई सामान्य प्रधान गुणांक नहीं है, इसलिए वे सह-प्रधान हैं।

प्रश्न 2: क्या पहला संख्या दूसरे द्वारा विभाज्य है? प्रधान गुणनखंड का उपयोग करें। (a) 225 और 27 उत्तर: नहीं, 225 27 द्वारा विभाज्य नहीं है।

व्याख्या: 225 का प्रधान गुणनखंड 3 × 3 × 5 × 5 है, और 27 का प्रधान गुणनखंड 3 × 3 × 3 है। चूंकि 225 में केवल दो 3 हैं, यह 27 द्वारा विभाज्य नहीं हो सकता, जो तीन 3 की आवश्यकता है।

(b) 96 और 24 उत्तर: हाँ, 96 24 द्वारा विभाज्य है।

व्याख्या: 96 का प्रधान गुणनखंड 2 × 2 × 2 × 2 × 2 × 3 है, और 24 का प्रधान गुणनखंड 2 × 2 × 2 × 3 है। चूंकि 96 में 24 के सभी गुणांक हैं, यह 24 द्वारा विभाज्य है।

(c) 343 और 17 उत्तर: नहीं, 343 17 द्वारा विभाज्य नहीं है।

व्याख्या: 343 का प्रधान गुणनखंड 7 × 7 × 7 है, और 17 एक प्रधान संख्या है जिसका 343 के साथ कोई सामान्य गुणांक नहीं है, इसलिए यह 17 द्वारा विभाज्य नहीं है।

(d) 999 और 99 उत्तर: नहीं, 999 99 द्वारा विभाज्य नहीं है।

व्याख्या: 999 का प्रधान गुणनखंड 3 × 3 × 3 × 37 है, और 99 का प्रधान गुणनखंड 3 × 3 × 11 है। उनके पास सभी गुणांक साझा नहीं हैं, और 37 11 द्वारा विभाज्य नहीं है। इसलिए, 999 99 द्वारा विभाज्य नहीं है।

प्रश्न 3: पहले संख्या का प्रमुख गुणनखंड 2 × 3 × 7 है और दूसरी संख्या का प्रमुख गुणनखंड 3 × 7 × 11 है। क्या ये सह-प्राइम हैं? क्या इनमें से कोई एक दूसरे को विभाजित करता है?

उत्तर: पहले संख्या के प्रमुख गुणनखंड = 2 × 3 × 7
दूसरे संख्या के प्रमुख गुणनखंड = 3 × 7 × 11
दोनों संख्याएँ सह-प्राइम नहीं हैं क्योंकि उनके पास 3 और 7 सामान्य गुणनखंड हैं। पहले संख्या में प्रमुख गुणनखंड 11 की कमी है और दूसरी संख्या में प्रमुख संख्या 2 की कमी है। इसलिए, इनमें से कोई भी एक दूसरे को विभाजित नहीं करता।

प्रश्न 4: गुणा कहता है, "किसी भी दो प्रमुख संख्याएँ सह-प्राइम होती हैं।" क्या वह सही है?

उत्तर: हाँ, गुणा सही है।

व्याख्या: किसी भी दो भिन्न प्रमुख संख्याओं के पास 1 के अलावा कोई सामान्य गुणनखंड नहीं होता, जिसका मतलब है कि वे हमेशा सह-प्राइम होती हैं।

पृष्ठ 123

प्रश्न: इस कथन पर विचार करें: 10 द्वारा विभाज्य संख्याएँ वे होती हैं जो 0 पर समाप्त होती हैं। क्या आप सहमत हैं?

उत्तर: हाँ, मैं सहमत हूँ। 10 द्वारा विभाज्य संख्याएँ हमेशा '0' पर समाप्त होती हैं। इसका कारण यह है कि 10, 2 और 5 का गुणनफल है, और किसी संख्या के 10 द्वारा विभाज्य होने के लिए, उसमें 2 और 5 दोनों को गुणनखंड के रूप में होना चाहिए। जब कोई संख्या 0 पर समाप्त होती है, तो यह इंगित करता है कि वह संख्या बिना शेष के 10 से विभाजित की जा सकती है। उदाहरण के लिए: 20, 30, 100 और 150 सभी 0 पर समाप्त होते हैं और ये 10 द्वारा विभाज्य हैं।

प्रश्न: इस कथन पर विचार करें: 5 द्वारा विभाज्य संख्याएँ वे होती हैं जो या तो '0' या '5' पर समाप्त होती हैं। क्या आप सहमत हैं?

उत्तर: हाँ, मैं सहमत हूँ। 5 द्वारा विभाज्य संख्याएँ हमेशा या तो '0' या '5' पर समाप्त होती हैं। इसका कारण यह है कि 5 के लिए विभाज्यता नियम बताता है कि किसी संख्या में 5 को उसके गुणनखंडों में से एक होना चाहिए। ऐसा होने के लिए, संख्या का अंतिम अंक या तो 0 या 5 होना चाहिए। उदाहरण के लिए: 15, 25, 40 और 55 सभी 5 द्वारा विभाज्य हैं क्योंकि वे 5 या 0 पर समाप्त होते हैं।

पृष्ठ 124

प्रश्न: इस कथन पर विचार करें: 2 से विभाज्य संख्या वे हैं जो '0', '2', '4', '6' या '8' पर समाप्त होती हैं। क्या आप सहमत हैं? 399 और 411 के बीच सभी 2 के गुणांक क्या हैं? उत्तर: हाँ, मैं सहमत हूँ। 2 से विभाज्य संख्या वे हैं जो '0', '2', '4', '6' या '8' पर समाप्त होती हैं। यह इसलिए है क्योंकि किसी संख्या के 2 से विभाज्य होने के लिए, उसे एक सम संख्या होना चाहिए, और सभी सम संख्याएँ इन अंकों में समाप्त होती हैं। 399 और 411 के बीच 2 के गुणांक हैं: 400, 402, 404, 406, 408 और 410। ये संख्याएँ 0, 2, 4, 6 या 8 पर समाप्त होती हैं, जो पुष्टि करती है कि वे 2 से विभाज्य हैं।

प्रश्न: 330 और 340 के बीच ऐसी संख्याएँ खोजें जो 4 से विभाज्य हों। इसके अलावा, 1730 और 1740 तथा 2030 और 2040 के बीच ऐसी संख्याएँ खोजें जो 4 से विभाज्य हों। आप क्या देखते हैं? उत्तर: 330 और 340 के बीच जो संख्याएँ 4 से विभाज्य हैं, वे हैं 332, 336, और 340। 1730 और 1740 के बीच जो संख्याएँ 4 से विभाज्य हैं, वे हैं 1732, 1736, और 1740। 2030 और 2040 के बीच जो संख्याएँ 4 से विभाज्य हैं, वे हैं 2032, 2036, और 2040।

प्रश्न: क्या 8536, 4 से विभाज्य है? उत्तर: चूंकि 8536 के अंतिम दो अंक (जो 36 हैं) 4 से विभाज्य हैं, इसलिए मूल संख्या 8536 भी 4 से विभाज्य है।

प्रश्न: इन कथनों पर विचार करें: (a) केवल अंतिम दो अंक महत्वपूर्ण हैं जब यह तय करने की बात आती है कि कोई संख्या 4 से विभाज्य है। (b) यदि अंतिम दो अंकों द्वारा बनाई गई संख्या 4 से विभाज्य है, तो मूल संख्या भी 4 से विभाज्य है। (c) यदि मूल संख्या 4 से विभाज्य है, तो अंतिम दो अंकों द्वारा बनाई गई संख्या भी 4 से विभाज्य है। क्या आप सहमत हैं? क्यों या क्यों नहीं? उत्तर: (a) हाँ, यह सही है। जब यह तय किया जाता है कि कोई संख्या 4 से विभाज्य है या नहीं, तो केवल संख्या के अंतिम दो अंक महत्वपूर्ण होते हैं। यह इसलिए है क्योंकि 100, 4 से विभाज्य है, इसलिए 4 के लिए विभाजन का नियम इस बात पर केंद्रित होता है कि अंतिम दो अंकों द्वारा बनाई गई संख्या 4 से विभाज्य है या नहीं। (b) हाँ, यह सही है। यदि किसी संख्या के अंतिम दो अंकों द्वारा बनाई गई संख्या 4 से विभाज्य है, तो मूल संख्या भी 4 से विभाज्य है। (c) हाँ, यह सही है। यदि मूल संख्या 4 से विभाज्य है, तो संख्या के अंतिम दो अंक भी निश्चित रूप से 4 से विभाज्य होंगे।

पृष्ठ 125

प्रश्न: 120 और 140 के बीच वे संख्याएँ खोजें जो 8 से विभाजित होती हैं। इसके अलावा 1120 और 1140, तथा 3120 और 3140 के बीच वे संख्याएँ खोजें जो 8 से विभाजित होती हैं। आप क्या देखते हैं? उत्तर: 8 से विभाजित संख्याएँ: 120 और 140 के बीच: 120, 128 और 136। 1120 और 1140 के बीच: 1120, 1128 और 1136। 3120 और 3140 के बीच: 3120, 3128 और 3136। अवलोकन: 8 से विभाजित संख्याएँ विभिन्न श्रेणियों में समान पैटर्न का पालन करती हैं, जो 8 के अंतराल पर होती हैं।

प्रश्न: 8560 के अंतिम दो अंकों को इस प्रकार बदलें कि परिणामी संख्या 8 का गुणांक हो। उत्तर: 8560 के अंतिम दो अंक "60" हैं, जो 8 से विभाजित नहीं होते। अंतिम दो अंकों को "64" में बदलने से यह 8 से विभाजित हो जाता है। नई संख्या 8564 है, जो 8 का गुणांक है।

प्रश्न: इस कथन पर विचार करें: (a) एक दिए गए संख्या के 8 से विभाजित होने का निर्णय लेते समय केवल अंतिम तीन अंक महत्वपूर्ण हैं। (b) यदि अंतिम तीन अंकों द्वारा बनाई गई संख्या 8 से विभाजित है, तो मूल संख्या भी 8 से विभाजित है। (c) यदि मूल संख्या 8 से विभाजित है, तो अंतिम तीन अंकों द्वारा बनाई गई संख्या भी 8 से विभाजित है। क्या आप सहमत हैं? क्यों या क्यों नहीं? उत्तर: (a) गलत। क्योंकि 8 से विभाज्यता की जाँच करते समय केवल अंतिम दो अंक महत्वपूर्ण होते हैं, क्योंकि हम 2 की शक्तियों से संबंधित हैं। (b) सही। क्योंकि यदि अंतिम तीन अंक 8 से विभाजित हैं, तो पूरी संख्या भी 8 से विभाजित है। (c) सही। क्योंकि यदि पूरी संख्या 8 से विभाजित है, तो इसके अंतिम तीन अंक भी 8 से विभाजित होंगे।

प्रश्न 1: 2024 एक लीप वर्ष है (क्योंकि फरवरी में 29 दिन होते हैं)। लीप वर्ष वे वर्ष होते हैं जो 4 के गुणांक होते हैं, सिवाय उन वर्षों के जो 100 से पूरी तरह विभाजित होते हैं लेकिन 400 से नहीं। (a) आपके जन्म के वर्ष से अब तक, कौन-कौन से वर्ष लीप वर्ष थे? उत्तर: वर्ष 2010 से 2024 तक, 4 लीप वर्ष हैं: 2012, 2016, 2020 और 2024।

• (a) दो सम संख्याओं का योग 4 का गुणांक देता है। उत्तर: कभी-कभी सत्य। किसी भी दो सम संख्याओं का योग हमेशा 4 से विभाज्य नहीं होता। उदाहरण के लिए, 6 + 4 = 10 जो 4 से विभाज्य नहीं है जबकि 2 + 2 = 4 जो 4 से विभाज्य है।
• (b) दो विषम संख्याओं का योग 4 का गुणांक देता है। उत्तर: कभी-कभी सत्य। दो विषम संख्याओं का योग वास्तव में सम हो सकता है लेकिन अनिवार्य रूप से 4 का गुणांक नहीं हो सकता। उदाहरण के लिए, 1 + 5 = 6 जो 4 का गुणांक नहीं है जबकि 1 + 3 = 4, जो 4 का गुणांक है। इसी प्रकार 7 + 5 = 12, जो 4 का गुणांक है।

पृष्ठ 126

Q4: निम्नलिखित संख्याओं को i) 10, ii) 5, iii) 2 से विभाजित करने पर प्राप्त शेषफल खोजें। 78, 99, 173, 572, 980, 1111, 2345। उत्तर:

• (i) 78 को 10 से विभाजित करने पर: शेषफल = 8 5 से विभाजित करने पर: शेषफल = 3 2 से विभाजित करने पर: शेषफल = 0
• (ii) 99 को 10 से विभाजित करने पर: शेषफल = 9 5 से विभाजित करने पर: शेषफल = 4 2 से विभाजित करने पर: शेषफल = 1
• (iii) 173 को 10 से विभाजित करने पर: शेषफल = 3 5 से विभाजित करने पर: शेषफल = 3 2 से विभाजित करने पर: शेषफल = 1
• (iv) 572 को 10 से विभाजित करने पर: शेषफल = 2 5 से विभाजित करने पर: शेषफल = 2 2 से विभाजित करने पर: शेषफल = 0
• (v) 980 को 10 से विभाजित करने पर: शेषफल = 0 5 से विभाजित करने पर: शेषफल = 0 2 से विभाजित करने पर: शेषफल = 0
• (vi) 1111 को 10 से विभाजित करने पर: शेषफल = 1 5 से विभाजित करने पर: शेषफल = 1 2 से विभाजित करने पर: शेषफल = 1
• (vii) 2345 को 10 से विभाजित करने पर: शेषफल = 5 5 से विभाजित करने पर: शेषफल = 0 2 से विभाजित करने पर: शेषफल = 1

Q5: शिक्षक ने पूछा कि क्या 14560 सभी 2, 4, 5, 8, और 10 से विभाज्य है। गुणा ने केवल दो इन संख्याओं के लिए 14560 के विभाजन की जांच की और फिर घोषित किया कि यह सभी से विभाज्य है। वे दो संख्याएँ क्या हो सकती हैं? उत्तर: 14560 का 2, 4, 5, 8 और 10 से विभाज्यता: जांचने के लिए दो महत्वपूर्ण संख्याएँ 4 और 5 होंगी। यदि कोई संख्या 4 और 5 से विभाज्य है, तो यह 2, 8 और 10 से भी विभाज्य होनी चाहिए।

Q6: निम्नलिखित में से कौन से संख्या 2, 4, 5, 8 और 10 द्वारा विभाज्य हैं: 572, 2352, 5600, 6000, 77622160? उत्तर: 2, 4, 5, 8 और 10 द्वारा विभाज्य: 5600, 6000 और 77622160।

(i) 572

• 2 पर समाप्त होता है: 2 द्वारा विभाज्य।
• अंतिम दो अंक 72 हैं: 4 द्वारा विभाज्य।
• 0 या 5 पर समाप्त नहीं होता: 5 द्वारा विभाज्य नहीं।
• अंतिम तीन अंक 572 हैं: 8 द्वारा विभाज्य नहीं।
• 0 पर समाप्त नहीं होता: 10 द्वारा विभाज्य नहीं।

(ii) 2352

• अंतिम दो अंक 52 हैं: 4 द्वारा विभाज्य।
• अंतिम तीन अंक 352 हैं: 8 द्वारा विभाज्य नहीं।

(iii) 5600

• 0 पर समाप्त होता है: 2 द्वारा विभाज्य।
• अंतिम दो अंक 00 हैं: 4 द्वारा विभाज्य।
• 0 पर समाप्त होता है: 5 द्वारा विभाज्य।
• अंतिम तीन अंक 600 हैं: 8 द्वारा विभाज्य।
• 0 पर समाप्त होता है: 10 द्वारा विभाज्य।

(iv) 6000

• अंतिम तीन अंक 000 हैं: 8 द्वारा विभाज्य।

(v) 77622160

• अंतिम दो अंक 60 हैं: 4 द्वारा विभाज्य।
• अंतिम तीन अंक 160 हैं: 8 द्वारा विभाज्य।

व्याख्या: ये संख्याएँ सभी गुणांक द्वारा विभाज्य हैं क्योंकि वे 2, 4, 5, 8 और 10 द्वारा विभाज्यता की शर्तों को पूरा करती हैं।

Q7: दो संख्याएँ लिखिए जिनका गुणनफल 10000 है। इन दोनों संख्याओं का इकाई अंक 0 नहीं होना चाहिए। उत्तर: 10000 के प्रमुख गुणांक = 2×2×2×2×5×5

= (2×2×2×2)×(5×5)

= 16 × 625

इसलिए, 16 और 625 वे दो संख्याएँ हैं जिनका इकाई अंक '0' नहीं है और जो मिलकर 10000 बनाती हैं।