Important Formulas: प्राइम टाइम | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

1. सामान्य गुणांक: वे संख्याएँ जो दो या दो से अधिक दिए गए संख्याओं के गुणांक होते हैं। उदाहरण: संख्याएँ 3 और 5 के लिए, सामान्य गुणांक 15, 30, और 45 जैसी संख्याएँ हैं। ये संख्याएँ 3 और 5 दोनों से विभाज्य हैं।

2. गुणांक: एक संख्या दूसरी संख्या का गुणांक है यदि वह दूसरी संख्या को बिना शेषफल के विभाजित करती है। उदाहरण के लिए, 4, 12 का गुणांक है क्योंकि 12 ÷ 4 = 3।

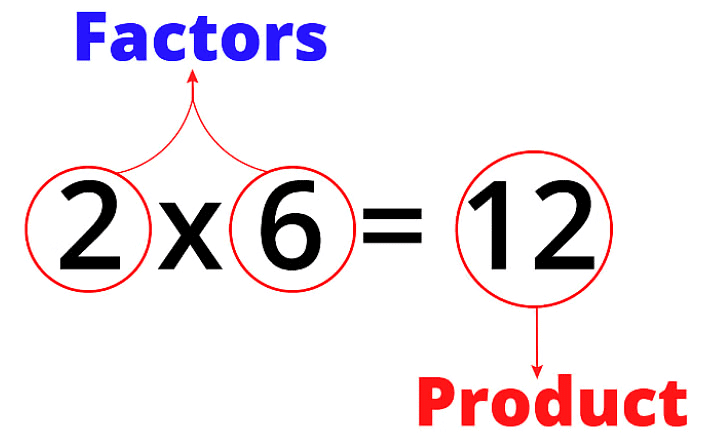
3. सामान्य गुणांक: एक सामान्य गुणांक वह संख्या है जो सेट में प्रत्येक संख्या को समान रूप से विभाजित कर सकती है। उदाहरण: संख्या 4, 12 और 16 का सामान्य गुणांक है क्योंकि 12 ÷ 4 = 3 और 16 ÷ 4 = 4।

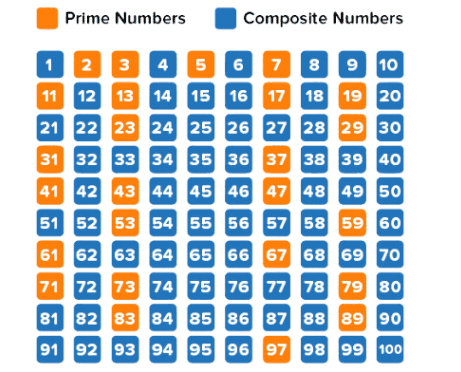
4. अभाज्य संख्याएँ: एक अभाज्य संख्या वह संख्या है जो 1 और स्वयं के अलावा किसी और संख्या से समान रूप से विभाजित नहीं होती। उदाहरण के लिए, 7 एक अभाज्य संख्या है क्योंकि 7 को समान रूप से विभाजित करने वाली केवल 1 और 7 ही संख्याएँ हैं।

5. समग्र संख्याएँ: एक समग्र संख्या वह होती है जिसमें दो से अधिक गुणांक होते हैं। इसका मतलब है कि इसे 1, स्वयं और कम से कम एक अन्य संख्या द्वारा समान रूप से विभाजित किया जा सकता है। उदाहरण के लिए, 12 समग्र है क्योंकि इसे 1, 2, 3, 4, 6, और 12 द्वारा विभाजित किया जा सकता है।

6. अभाज्य गुणनखंडन: 1 से बड़ी प्रत्येक संख्या को अभाज्य संख्याओं के गुणन के रूप में व्यक्त किया जा सकता है। उदाहरण के लिए, 84 = 2 × 2 × 3 × 7।

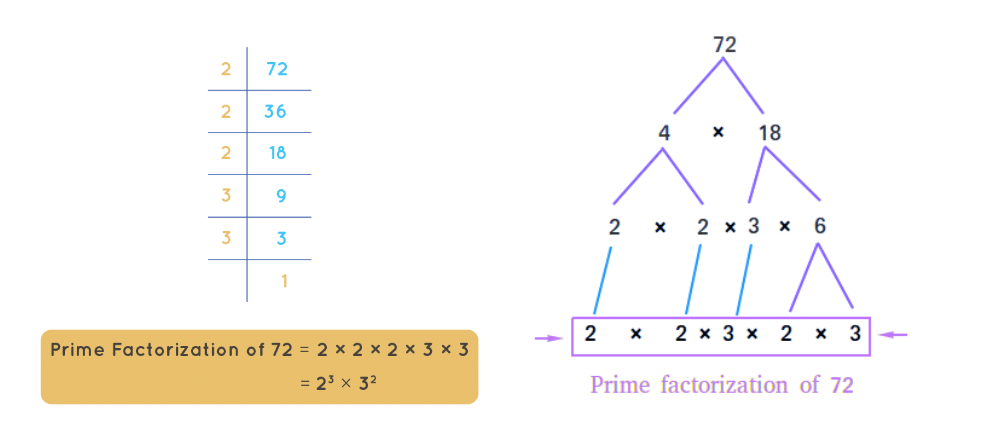
7. अद्वितीय गुणनखंडन: एक संख्या को अभाज्य संख्याओं में गुणन करने का केवल एक ही तरीका होता है, हालांकि गुणांक का क्रम भिन्न हो सकता है।

8. सह-प्राइम संख्याएँ: दो संख्याएँ सह-प्राइम होती हैं यदि उनके पास 1 के अलावा कोई सामान्य गुणांक नहीं होता।

9. सह-प्रायमिता की जाँच: यह निर्धारित करने के लिए कि क्या दो संख्याएँ सह-प्राइम हैं, उनके अभाज्य गुणनखंडन को खोजें। यदि कोई सामान्य अभाज्य गुणांक नहीं है, तो वे सह-प्राइम हैं। उदाहरण:

80 = 2 × 2 × 2 × 2 × 563 = 3 × 3 × 7

10. गुणांक समावेशन: एक संख्या दूसरी संख्या का गुणांक होती है यदि उसकी प्राइम फैक्टराइजेशन दूसरी संख्या की प्राइम फैक्टराइजेशन का भाग हो।

11. विभाजन परीक्षण:

• 10 से विभाजन: एक संख्या 10 से विभाज्य होती है यदि उसका अंतिम अंक 0 है।
• 5 से विभाजन: एक संख्या 5 से विभाज्य होती है यदि उसका अंतिम अंक 0 या 5 है।
• 2 से विभाजन: एक संख्या 2 से विभाज्य होती है यदि उसका अंतिम अंक सम (0, 2, 4, 6, 8) है।
• 4 से विभाजन: एक संख्या 4 से विभाज्य होती है यदि उसके अंतिम दो अंकों द्वारा बनाई गई संख्या 4 से विभाज्य है।
• 8 से विभाजन: एक संख्या 8 से विभाज्य होती है यदि उसके अंतिम तीन अंकों द्वारा बनाई गई संख्या 8 से विभाज्य है।

12. विशेष संख्याएँ:

• पूर्ण वर्ग: एक संख्या जो किसी पूर्णांक का वर्ग है (उदाहरण: 9 = 3 × 3)।
• प्राइम संख्या: एक संख्या जो 1 से बड़ी होती है और जिसका कोई सकारात्मक विभाजक 1 और स्वयं के अलावा नहीं होता (उदाहरण: 43, 7)।
• पूर्ण घन: एक संख्या जो किसी पूर्णांक का घन है (उदाहरण: 27 = 3 × 3 × 3)।