परिमाप और क्षेत्रफल Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

परिचय

यह अध्याय परिधि और क्षेत्रफल के बारे में है—दो महत्वपूर्ण तरीके जो आकृतियों और उनके द्वारा लिए गए स्थान को समझने में मदद करते हैं। परिधि हमें यह बताती है कि किसी आकृति के चारों ओर कितनी दूरी है, जैसे कि बगीचे के चारों ओर बाड़ की लंबाई को मापना। क्षेत्रफल हमें यह बताता है कि किसी आकृति के अंदर कितना स्थान है, जैसे कि यह पता करना कि एक दीवार को रंगने के लिए कितना रंग चाहिए। इन अवधारणाओं को सीखने से आप असली जीवन की समस्याओं को हल कर सकेंगे, जैसे कि खेल के मैदान का डिज़ाइन करना या अपने कमरे को सजाना, और आप अपने चारों ओर की दुनिया में गणित को देख पाएंगे।

परिधि

• एक बंद समतल आकृति की परिधि उस सीमा के चारों ओर की कुल दूरी है जब आप इसके चारों ओर एक बार जाते हैं।
• एक बहुभुज के लिए, जो सीधे रेखा खंडों से बनी एक बंद आकृति है, परिधि सरलता से इसके सभी किनारों की लंबाई का योग होती है। इसका मतलब है कि आप प्रत्येक किनारे की लंबाई को जोड़ते हैं ताकि आकृति के बाहरी किनारे के चारों ओर कुल दूरी प्राप्त हो सके।
• परिधि का सूत्र: परिधि = सभी किनारों की लंबाई का योग।
• परिधि की अवधारणा का वास्तविक जीवन में व्यापक रूप से उपयोग किया जाता है। उदाहरण: भूमि की बाड़ लगाने के लिए। घर के चारों ओर एक कंपाउंड दीवार बनाने के लिए।

आयत की परिधि

• आयत की परिधि: परिधि = लंबाई + चौड़ाई + लंबाई + चौड़ाई।
• परिधि = 2 x (लंबाई + चौड़ाई)।
• आयत की परिधि उसकी लंबाई और चौड़ाई के योग का दो गुना होती है।

उदाहरण: कल्पना करें कि आपके पास एक आयताकार बगीचा है। बगीचा 12 सेंटीमीटर लंबा और 8 सेंटीमीटर चौड़ा है। आप इसके चारों ओर एक बाड़ लगाना चाहते हैं। यह पता करने के लिए कि आपको कितनी बाड़ की आवश्यकता है, आपको आयत की परिधि की गणना करनी होगी।

समाधान: परिमाप बाग के चारों ओर की कुल दूरी है, जो सभी चार किनारों का योग है। इसे इस प्रकार गणना करते हैं:

चरण 1: लंबाई और चौड़ाई को एक साथ जोड़ें।

• लंबाई (AB) = 12 सेमी
• चौड़ाई (BC) = 8 सेमी
• AB + BC = 12 सेमी + 8 सेमी = 20 सेमी

चरण 2: चूंकि आयत के दो लंबाई और दो चौड़ाई होते हैं, इसलिए योग को 2 से गुणा करें।

• परिमाप = 2 × (लंबाई + चौड़ाई)
• परिमाप = 2 × 20 सेमी = 40 सेमी

इसलिए, बाग का परिमाप 40 सेमी है।

वर्ग का परिमाप

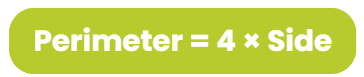
• वर्ग का परिमाप = 4 × एक किनारे की लंबाई। वर्ग का परिमाप उसके किनारे की लंबाई का चौगुना होता है।

उदाहरण: डेबोजीत के पास एक वर्ग फोटो फ्रेम है, और फ्रेम के प्रत्येक किनारे की लंबाई 1 मीटर है। वह चाहते हैं कि वह फ्रेम के चारों ओर रंगीन टेप लगाएं। यह जानने के लिए कि उन्हें कितनी टेप की आवश्यकता है, हम वर्ग का परिमाप निकालते हैं।

समाधान: एक वर्ग के लिए, सभी चार किनारे समान लंबाई के होते हैं। परिमाप केवल एक किनारे की लंबाई का चार गुना है:

चरण 1: एक किनारे की लंबाई को 4 से गुणा करें।

• परिमाप = 4 × किनारा
• परिमाप = 4 × 1 मीटर = 4 मीटर

इसलिए, डेबोजीत को फोटो फ्रेम के चारों ओर लगाने के लिए 4 मीटर टेप की आवश्यकता है।

त्रिकोण का परिमाप

उदाहरण: मान लीजिए आपके पास एक त्रिकोण है, जिसके किनारे 4 सेमी, 5 सेमी, और 7 सेमी लंबे हैं। आप इस त्रिकोण का परिमाप जानना चाहते हैं।

समाधान: परिमाप सभी तीन किनारों की लंबाई का योग है:

• परिमाप = 4 सेमी + 5 सेमी + 7 सेमी = 16 सेमी

इसलिए, त्रिकोण का परिमाप 16 सेमी है।

रेखाओं द्वारा निर्मित आकृतियों का परिमाप

\"F\" अक्षर की आकृतियाँ ग्रिड पर रेखाओं का उपयोग करके बनाई गई हैं। प्रत्येक अक्षर का परिमाप ज्ञात करने के लिए, हमें उस आकृति के सभी किनारों की लंबाई को मापना होगा।

• सीधी रेखाएँ (s): ये रेखाएँ क्षैतिज या ऊर्ध्वाधर दिशा में चलती हैं।
• तिरछी रेखाएँ (d): ये रेखाएँ बिंदुओं को तिरछी दिशा में जोड़ती हैं, जिससे एक झुकी हुई रेखा बनती है।
• आप सीधी इकाइयों (s) और तिरछी इकाइयों (d) की संख्या गिनते हैं।
• इन्हें जोड़कर \"s d इकाइयाँ\" के रूप में कुल परिमाप प्राप्त करें।

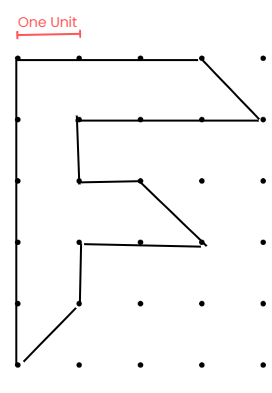
ग्रिड में \"F\" की इस छवि के लिए, 16 सीधी और 3 तिरछी रेखाएँ हैं।

• सीधी रेखाएँ (s) = 16
• तिरछी रेखाएँ (d) = 3
• कुल परिमाप = s d = 16 3 = 19 इकाइयाँ

कुल परिमाप = s d = 16 3 = 19 इकाइयाँ

सरल उदाहरणों के साथ परिमाप को समझना

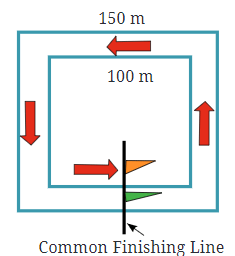
उदाहरण: गहरा गोताखोरी। अब, कल्पना करें कि आप एक खेल के मैदान में हैं जहाँ दो रास्ते हैं जिन पर आप दौड़ सकते हैं। एक रास्ता बड़ा है, और दूसरा छोटा। आप और आपका मित्र विभिन्न रास्तों पर दौड़ने का निर्णय लेते हैं और देखते हैं कि कौन अधिक दौड़ता है।

• बड़ा रास्ता: यह 50 मीटर लंबा और 30 मीटर चौड़ा है। एक चक्कर में आप कितनी दूर दौड़ते हैं, यह जानने के लिए, आप इस रास्ते का परिमाप निकालते हैं।
• बड़े रास्ते का परिमाप = 2 × (लंबाई × चौड़ाई) = 2 × (50 मीटर × 30 मीटर) = 2 × 80 मीटर = 160 मीटर।
• तो, यदि आप एक बार बड़े रास्ते के चारों ओर दौड़ते हैं, तो आप 160 मीटर दौड़ते हैं।
• छोटा रास्ता: यह 30 मीटर लंबा और 20 मीटर चौड़ा है।
• छोटे रास्ते का परिमाप = 2 × (लंबाई × चौड़ाई) = 2 × (30 मीटर × 20 मीटर) = 2 × 50 मीटर = 100 मीटर।

यदि आपका मित्र एक बार छोटे रास्ते के चारों ओर दौड़ता है, तो वह 100 मीटर दौड़ता है।

अब, यदि आप बड़े पथ पर 3 चक्र दौड़ते हैं, तो आप दौड़ेंगे: 3 × 160 मीटर = 480 मीटर। और यदि आपका दोस्त छोटे पथ पर 4 चक्र दौड़ता है, तो वह दौड़ेगा: 4 × 100 मीटर = 400 मीटर। इसलिए, हालांकि आपके दोस्त ने अधिक चक्र दौड़े, आपने लंबी दूरी (480 मीटर बनाम 400 मीटर) तय की।

उदाहरण: सरल दौड़ के साथ दूरी की तुलना

मान लीजिए कि आप और आपका दोस्त दो ट्रैक के चारों ओर दौड़ने जा रहे हैं, लेकिन ये ट्रैक आयत के बजाय वर्ग हैं:

• बड़ा वर्ग ट्रैक: प्रत्येक पक्ष की लंबाई 40 मीटर है।
• छोटा वर्ग ट्रैक: प्रत्येक पक्ष की लंबाई 20 मीटर है।
• बड़े वर्ग ट्रैक का परिमिति = 4 × पक्ष = 4 × 40 मीटर = 160 मीटर
• छोटे वर्ग ट्रैक का परिमिति = 4 × पक्ष = 4 × 20 मीटर = 80 मीटर

यदि दौड़ की लंबाई 240 मीटर है, तो आपको यह पता लगाना होगा कि आपको कहाँ से शुरू करना है ताकि आप दोनों एक ही स्थान पर समाप्त करें:

• बड़े ट्रैक पर, 240 मीटर दौड़ने के बाद, आप अपने प्रारंभिक बिंदु से 240 - 160 = 80 मीटर पर होंगे।
• छोटे ट्रैक पर, 240 मीटर दौड़ने के बाद, आप अपने प्रारंभिक बिंदु से 240 - 80 = 160 मीटर पर होंगे।

अनुमान और सत्यापन

एक कागज़ या समाचार पत्र लें और इसे विभिन्न आकारों, जैसे सितारे, दिल या त्रिकोण में काटें।

• पहले, अनुमान लगाएँ कि प्रत्येक आकार के किनारे (या परिमिति) कितने लंबे हैं। फिर, एक पैमाने या मापने वाली टेप का उपयोग करके वास्तविक परिमिति मापें।

देखें कि आपका अनुमान कितना करीब था!

नियमित बहुभुज का परिमिति

एक नियमित बहुभुज एक बंद आकृति है जहाँ सभी पक्ष और सभी कोण समान होते हैं। उदाहरण के लिए:

समान्तर त्रिकोण: सभी तीन भुजाएँ और सभी तीन कोण समान होते हैं।

वर्ग: सभी चार भुजाएँ और सभी चार कोण समान होते हैं।

समान्तर त्रिकोण का परिमाप

किसी भी त्रिकोण का परिमाप उसकी तीन भुजाओं का योग होता है। एक समान्तर त्रिकोण के लिए, चूंकि सभी तीन भुजाएँ समान होती हैं, परिमाप होगा:

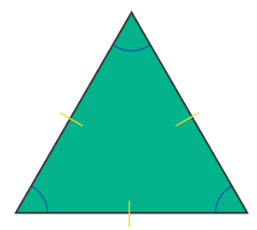
उदाहरण: कल्पना कीजिए कि आपके पास एक समान्तर त्रिकोण है जिसकी प्रत्येक भुजा 5 सेमी है। परिमाप होगा: परिमाप = 3 × 5 सेमी = 15 सेमी

वर्ग और समान्तर त्रिकोण के बीच समानता

• दोनों आकृतियों के पास समान भुजाएँ और समान कोण होते हैं, जिससे वे नियमित बहुभुज बनती हैं।
• प्रत्येक का परिमाप उसकी भुजाओं की संख्या को एक भुजा की लंबाई से गुणा करके निकाला जा सकता है।

फटने और फिर से जोड़ने की गतिविधि: आपके पास 6 सेमी × 4 सेमी आकार का एक आयताकार कागज़ है।

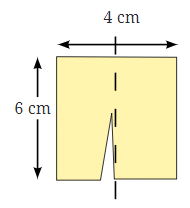
इस आयत को दो समान टुकड़ों में काटा गया है और नए आकार बनाने के लिए विभिन्न तरीकों से फिर से जोड़ा गया है। आपका कार्य प्रत्येक नए आकार का परिमाप निकालना है।

उदाहरण अ:

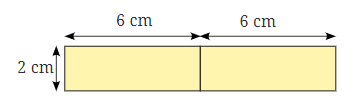
पहले व्यवस्था के लिए, टुकड़े एक-दूसरे के बगल में जुड़े हैं, जिससे एक लंबा आयत बनता है। परिमाप होगा:

व्यवस्था अ का परिमाप:

• ऊपर: 6 सेमी
• नीचे: 6 सेमी
• बाएं: 2 सेमी
• दाएं: 2 सेमी
• कुल परिमाप = 6 सेमी + 6 सेमी + 2 सेमी + 2 सेमी = 28 सेमी

उदाहरण ब, स, और द:

अब, चलिए इन नए आकारों के लिए परिमाप की गणना करते हैं:

ब.

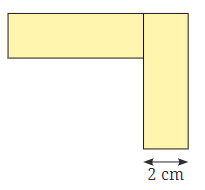
उत्तर:

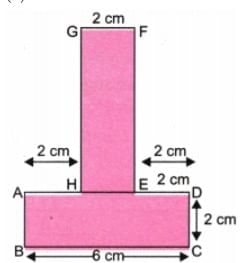
सीमा की लंबाई = AB BC CD DE EF FG GA = 6 2 6 2 4 6 2 = 28 सेमी

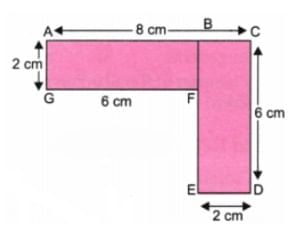
c.

कुल सीमा की लंबाई = AB BC CD DE EF FG GH HA = 2 6 2 2 6 2 6 2 = 28 सेमी

उत्तर:

कुल सीमा की लंबाई = AB BC CD DE EF FG GH HA = 6 2 3 2 6 2 3 2 = 26 सेमी

क्षेत्रफल

किसी बंद आकृति के द्वारा घिरे क्षेत्र को उसका क्षेत्रफल कहा जाता है।

मुख्य सूत्र

• वर्ग का क्षेत्रफल: वर्ग का क्षेत्रफल एक भुजा की लंबाई को स्वयं से गुणा करके निकाला जाता है।
• आयत का क्षेत्रफल: आयत का क्षेत्रफल लंबाई और चौड़ाई को गुणा करके प्राप्त किया जाता है।

उदाहरणों के साथ समझना

उदाहरण 1: फर्श पर अनकवर्ड क्षेत्र का पता लगाना

कल्पना करें कि आपके पास एक आयत कक्ष है जिसकी लंबाई 5 मीटर और चौड़ाई 4 मीटर है। आप फर्श के बीच में 3 मीटर प्रत्येक भुजा वाला एक वर्ग कालीन रखते हैं। फर्श का कितना हिस्सा कालीन द्वारा कवर नहीं किया गया है?

चरण-दर-चरण समाधान:

• फर्श का क्षेत्रफल निकालें:
  • फर्श की लंबाई: 5 मीटर
  • फर्श की चौड़ाई: 4 मीटर
  • फर्श का क्षेत्रफल: 5 मीटर × 4 मीटर = 20 वर्ग मीटर
• कालीन का क्षेत्रफल निकालें:
  • कालीन की भुजा: 3 मीटर
  • कालीन का क्षेत्रफल: 3 मीटर × 3 मीटर = 9 वर्ग मीटर
• अनकवर्ड क्षेत्र खोजें:
  • अनकवर्ड क्षेत्र: फर्श का क्षेत्रफल - कालीन का क्षेत्रफल
  • अनकवर्ड क्षेत्र: 20 वर्ग मीटर - 9 वर्ग मीटर = 11 वर्ग मीटर

तो, फर्श के 11 वर्ग मीटर हिस्से पर कालीन नहीं है।

वास्तविक जीवन में अनुप्रयोग: आप इसे घर पर आजमा सकते हैं! अपने कमरे का क्षेत्रफल मापें और फिर देखें कि आपके बिस्तर या टेबल द्वारा कितना स्थान लिया गया है। इससे आपको यह समझने में मदद मिलेगी कि आपके कमरे में कितना खाली स्थान बचा है।

असमान आकारों का क्षेत्रफल अनुमानित करना

छवि में दो आकारों पर ध्यान दें। आपको क्या लगता है कि इनमें से किसका क्षेत्रफल अधिक है? केवल देखने से यह बताना आसान नहीं है, है ना? इन असमान आकारों का क्षेत्रफल अनुमानित करने के लिए, हम वर्ग या ग्राफ पेपर का उपयोग कर सकते हैं। यह विधि तब सहायक होती है जब आकार सरल वर्ग या आयत नहीं होता।

ग्राफ पेपर का उपयोग करके क्षेत्रफल का अनुमान कैसे लगाएं:

• आकार का ट्रेस करें: सबसे पहले, आकार को एक पारदर्शक कागज पर ट्रेस करें। फिर, इस कागज को ग्राफ पेपर की एक शीट के ऊपर रखें। ग्राफ पेपर पर प्रत्येक छोटा वर्ग 1 वर्ग इकाई का प्रतिनिधित्व करता है।
• पूर्ण वर्गों की गणना करें: आकार के अंदर सभी पूर्ण वर्गों की गणना करें। इनमें से प्रत्येक पूर्ण वर्ग क्षेत्रफल में ठीक 1 वर्ग इकाई योगदान करता है।
• आंशिक वर्गों को संभालें:
  • आधा वर्ग से कम: इन्हें अनदेखा करें। ये क्षेत्रफल में योगदान नहीं करते।
  • आधे से अधिक वर्ग: इन्हें 1 वर्ग इकाई के रूप में गिनें।
  • सटीक आधा वर्ग: इन्हें 0.5 वर्ग इकाई (या ½ वर्ग इकाई) के रूप में गिनें।

इन चरणों का पालन करके, आप लगभग किसी भी आकार का क्षेत्रफल अनुमानित कर सकते हैं।

क्षेत्रफल को मापने के लिए वर्गों का उपयोग क्यों करें?

आप सोच सकते हैं कि हम क्षेत्रफल को मापने के लिए अन्य आकारों जैसे वृत्त या त्रिकोण के बजाय वर्गों का उपयोग क्यों करते हैं। आइए इसे समझें:

• वर्ग पूरी तरह से फिट होते हैं: जब आप क्षेत्र को वर्गों से ढकते हैं, तो कोई खाली स्थान या ओवरलैप नहीं होता। इससे माप सटीक होता है।
• वृत्त या अन्य आकार: यदि आप क्षेत्र को मापने के लिए वृत्तों का उपयोग करने की कोशिश करते हैं, तो आप यह देखेंगे कि वृत्त बिना खाली स्थान छोड़े एक साथ फिट नहीं होते। इससे क्षेत्रफल को सटीक रूप से मापना मुश्किल हो जाता है।

त्रिकोण का क्षेत्रफल

उदाहरण 1: चित्र में, आप एक आयत ABCD देख रहे हैं जिसमें एक विकर्ण रेखा BD है। यह विकर्ण आयत को दो त्रिकोणों में विभाजित करता है: नीला त्रिकोण BAD और पीला त्रिकोण BEC।

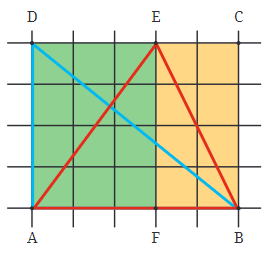
समाधान:

• कल्पना करें कि ग्राफ पेपर पर एक आयत ABCD है। आयत के कोनों को A, B, C, और D के रूप में लेबल किया गया है। विकर्ण रेखा B से D तक खींचकर आयत को दो त्रिकोणों में विभाजित किया गया है: त्रिकोण BAD और BCD।

आयत ABCD का क्षेत्रफल निकालना

• आयत का क्षेत्रफल निकालने के लिए, इसके भीतर के वर्ग इकाइयों की संख्या को गिनें। ग्राफ पेपर पर प्रत्येक वर्ग 1 वर्ग इकाई का प्रतिनिधित्व करता है। उदाहरण के लिए, यदि आयत A से B तक 5 वर्ग लंबी है और A से D तक 4 वर्ग चौड़ी है, तो क्षेत्रफल निम्नलिखित के अनुसार गणना की जाती है:
• ABCDA का क्षेत्रफल = लंबाई × चौड़ाई
• ABCDA का क्षेत्रफल = 5 वर्ग × 4 वर्ग = 20 वर्ग इकाइयाँ।

त्रिकोण BAD का क्षेत्रफल समझना

• त्रिकोण BAD आयत को विकर्ण BD के साथ काटकर बनाया गया है। चूंकि विकर्ण आयत को दो समान भागों में विभाजित करता है, त्रिकोण BAD का क्षेत्रफल आयत ABCD के क्षेत्रफल का आधा है।
• सूत्र: त्रिकोण BAD का क्षेत्रफल = ½ × आयत ABCD का क्षेत्रफल
• हमारे पिछले उदाहरण का उपयोग करते हुए, यदि ABCD का क्षेत्रफल 20 वर्ग इकाइयाँ हैं:
• त्रिकोण BAD का क्षेत्रफल = ½ × 20 वर्ग इकाइयाँ = 10 वर्ग इकाइयाँ।

त्रिकोण ABE का अन्वेषण करना

• त्रिकोण ABE आयत के भीतर एक और विकर्ण द्वारा बनाया गया है, जो इसे छोटे खंडों में विभाजित करता है।
• यह त्रिकोण आगे दो छोटे त्रिकोणों: AEF और BEF में विभाजित किया जा सकता है।
• त्रिकोण ABE का क्षेत्रफल त्रिकोणों AEF और BEF के क्षेत्रफल का योग है।
• इन छोटे त्रिकोणों (AEF और BEF) में से प्रत्येक, ABCD के भीतर फिट होने वाले छोटे आयतों के क्षेत्रफल का आधा है।

त्रिकोण ABE का विभाजन

• त्रिकोण AEF का क्षेत्रफल छोटे आयत AFED के क्षेत्रफल का आधा है।
• इसी तरह, त्रिकोण BEF का क्षेत्रफल छोटे आयत BFEC के क्षेत्रफल का आधा है।
• इसलिए, त्रिकोण ABE का क्षेत्रफल AFED और BFEC के क्षेत्रफल का आधा है।
• यह भी अर्थ रखता है कि त्रिकोण ABE का क्षेत्रफल बड़े आयत ABCD के क्षेत्रफल का आधा है।
• जब आप किसी आयत को उसके विकर्ण के साथ काटते हैं, तो आप दो त्रिकोण बनाते हैं, जिनमें से प्रत्येक का क्षेत्रफल ठीक आयत के क्षेत्रफल का आधा होता है।
• चाहे आप त्रिकोण BAD या ABE का सामना कर रहे हों, संबंध समान रहता है: दोनों त्रिकोण आयत ABCD के क्षेत्रफल का आधा कवर करते हैं।

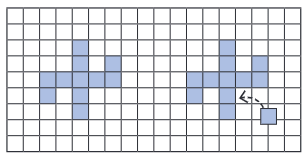
उदाहरण 2: इसे 'ज्यादा' या 'कम' बनाना

आपके द्वारा प्रदान किए गए चित्रों में, 9 इकाई वर्गों से बने दो आकृतियाँ हैं। प्रत्येक वर्ग का क्षेत्रफल 1 वर्ग इकाई है, इसलिए दोनों आकृतियों का कुल क्षेत्रफल 9 वर्ग इकाई है।

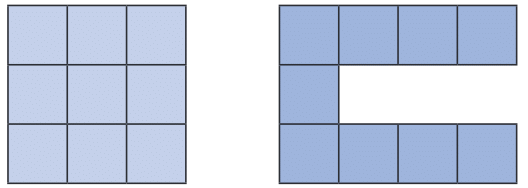
हालांकि, इन दोनों आकृतियों के परिमाप अलग हैं। पहले आकृति का परिमाप 12 इकाइयाँ है, और दूसरी आकृति का परिमाप 20 इकाइयाँ है। समाधान:

• 9 इकाई वर्गों के साथ परिमाप का अन्वेषण:
  • संभव सबसे छोटा परिमाप: सबसे छोटा परिमाप तब होता है जब आप वर्गों को सबसे संकुचित आकार में व्यवस्थित करते हैं। यह आमतौर पर तब होता है जब आप 3x3 वर्ग बनाते हैं। इस मामले में परिमाप 12 इकाइयाँ होगा।
  • संभव सबसे बड़ा परिमाप: सबसे बड़ा परिमाप तब होता है जब वर्गों को एकल रेखा में व्यवस्थित किया जाता है। इस मामले में परिमाप 20 इकाइयाँ होगा।
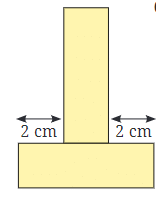
  • 18 इकाइयों के परिमाप वाली आकृति बनाना: आप वर्गों को विभिन्न आकारों में व्यवस्थित करके प्रयोग कर सकते हैं। 18 इकाइयों के परिमाप वाली एक संभावित आकृति "L" आकार की हो सकती है, जिसमें एक तरफ 2 वर्ग और दूसरी तरफ 3 वर्ग हों।
• आकृति में एक नया वर्ग जोड़ना: यदि आप 24 इकाइयों के परिमाप वाली आकृति में एक नया वर्ग जोड़ते हैं, तो परिमाप में परिवर्तन इस बात पर निर्भर करता है कि आप नया वर्ग कहाँ रखते हैं।
  • यदि परिमाप बढ़ता है: यह तब होता है जब नया वर्ग इस तरह से रखा जाता है कि यह आकृति के बाहरी किनारे पर अधिक पक्ष जोड़ता है।
  • यदि परिमाप घटता है: यह तब होता है यदि नया वर्ग किसी खाली जगह को भरता है, जिससे उजागर पक्षों की संख्या कम हो जाती है।
  • यदि परिमाप वही रहता है: यह तब होता है जब नया वर्ग मौजूदा पक्ष के साथ पूरी तरह से संरेखित होता है, जिससे बाहरी किनारे पर कोई नया पक्ष नहीं जुड़ता।

आकृति में एक नया वर्ग जोड़ना: यदि आप 24 इकाइयों के परिमाप वाली आकृति में एक नया वर्ग जोड़ते हैं, तो परिमाप में परिवर्तन इस बात पर निर्भर करता है कि आप नया वर्ग कहाँ रखते हैं।

मुख्य बिंदु

• परिमाप एक बंद आकृति के चारों ओर की कुल दूरी होती है।
• एक बहुभुज का परिमाप इसके सभी किनारों की लंबाइयों का योग होता है।
• एक आयत का परिमाप इस प्रकार निकाला जाता है: 2 × (लंबाई + चौड़ाई)।
• एक वर्ग का परिमाप इस प्रकार निकाला जाता है: 4 × एक किनारे की लंबाई।
• एक त्रिकोण का परिमाप इसके तीन किनारों की लंबाइयों का योग होता है।
• एक ग्रिड पर आकृतियों के लिए, परिमाप में सीधे और तिरछे दोनों रेखाएँ शामिल होती हैं।

• क्षेत्रफल एक बंद आकृति के अंदर का स्थान होता है, जिसे वर्ग इकाइयों में मापा जाता है।
• एक वर्ग का क्षेत्रफल इस प्रकार निकाला जाता है: किनारा × किनारा।
• एक आयत का क्षेत्रफल इस प्रकार निकाला जाता है: लंबाई × चौड़ाई।
• अनियमित आकृतियों के क्षेत्रफल का अनुमान लगाने के लिए ग्राफ पेपर का उपयोग किया जा सकता है, जिसमें पूर्ण और आंशिक वर्गों की गिनती की जाती है।
• एक आयत को तिरछा काटने पर दो त्रिकोण बनते हैं, प्रत्येक का क्षेत्रफल आयत का आधा होता है।
• एक घर की योजना का क्षेत्रफल और परिमाप खोजने के लिए, प्रत्येक कमरे का क्षेत्रफल निकालें और कुल क्षेत्र के लिए उन्हें जोड़ें; कुल परिमाप के लिए बाहरी किनारों का योग करें।
• घर की योजनाओं की तुलना में उनके कुल क्षेत्रफल और परिमाप की गणना और तुलना करना शामिल है।