परिमाप और क्षेत्रफल NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download
पृष्ठ 132
प्रश्न 1: गायब शब्दों को खोजें:
(क) आयत का परिमाप = 14 सेमी; चौड़ाई = 2 सेमी; लंबाई = ? उत्तर: हमें पता है कि आयत का परिमाप = 2(l + b) यहाँ, आयत का परिमाप = 14 सेमी और चौड़ाई b = 2 सेमी है, l =? इस प्रकार 14 = 2(l + 2) ⇒ 14 = 2l + 4 ⇒ 2l = 14 – 4 = 10 ⇒ l = 10/2 = 5 सेमी
(ख) वर्ग का परिमाप = 20 सेमी; भुजा की लंबाई = ? उत्तर: हमें पता है कि वर्ग का परिमाप = 4 × a जहाँ a = वर्ग की भुजा ∴ 20 = 4 × a ⇒ a = 5 सेमी
(ग) आयत का परिमाप = 12 मीटर; लंबाई = 3 मीटर; चौड़ाई = ? उत्तर: आयत का परिमाप = 2(l + b) ⇒ 12 = 2(3 + b) ⇒ 12 = 6 + 2b ⇒ 12 – 6 = 2b ⇒ 2b = 6 मीटर ⇒ b = 3 मीटर
प्रश्न 2: एक आयत जिसकी भुजाएँ 5 सेमी और 3 सेमी हैं, को एक तार से बनाया गया है। यदि तार को सीधा किया जाता है और फिर एक वर्ग बनाने के लिए मोड़ा जाता है, तो वर्ग की एक भुजा की लंबाई क्या होगी? उत्तर: यहाँ आयत का परिमाप = 2(5 + 3) = 2 × 8 = 16 सेमी। अब तार को सीधा किया जाता है और फिर एक वर्ग बनाने के लिए मोड़ा जाता है। ∴ वर्ग का परिमाप = 16 सेमी ⇒ 4a = 16 सेमी ⇒ a = 4 सेमी, वर्ग की भुजा की आवश्यक लंबाई।
प्रश्न 3: एक त्रिकोण की तीसरी भुजा की लंबाई खोजें, जिसका परिमाप 55 सेमी है और जिसकी दो भुजाएँ क्रमशः 20 सेमी और 14 सेमी हैं। उत्तर:
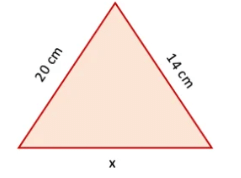
त्रिकोण की पहली भुजा = 20 सेमी। त्रिकोण की दूसरी भुजा = 14 सेमी। मान लें त्रिकोण की तीसरी भुजा 'x' है। त्रिकोण का परिमाप = 55 सेमी ∴ 20 + 14 + x = 55 सेमी। 34 + x = 55। x = 55 - 34। x = 21 सेमी। इसलिए, त्रिकोण की तीसरी भुजा की लंबाई 21 सेमी है।
प्रश्न 4: एक आयताकार पार्क की बाड़ लगाने की लागत क्या होगी, जिसकी लंबाई 150 मीटर और चौड़ाई 120 मीटर है, यदि बाड़ की कीमत ₹ 40 प्रति मीटर है? उत्तर: बाड़ की लंबाई आयताकार पार्क का परिमाप है। दिया गया है कि आयताकार पार्क की लंबाई = 150 मीटर और चौड़ाई = 120 मीटर। ∴ परिमाप = 2(l + b) = 2(150 + 120) = 2(270) = 540 मीटर। अब प्रति मीटर बाड़ लगाने की लागत = ₹ 40। आयताकार पार्क की बाड़ लगाने की लागत = ₹ 40 × 540 = ₹ 21600।
प्रश्न 5: एक तार की लंबाई 36 सेमी है। यदि इसका उपयोग किया जाए तो प्रत्येक भुजा की लंबाई क्या होगी: (क) एक वर्ग के लिए? उत्तर: दिया गया है, एक तार की लंबाई 36 सेमी है। ∴ वर्ग की प्रत्येक भुजा की लंबाई = a, परिमाप = 36 ⇒ 4a = 36 ⇒ a = 9 सेमी।
(b) सभी भुजाओं की लंबाई समान त्रिकोण
उत्तर: त्रिकोण की प्रत्येक भुजा की लंबाई = 3a (दी गई) परिधि = 36 ⇒ 3a = 36 ⇒ a = 12 सेमी
(c) समान भुजाओं वाला एक षट्कोण (छह भुजाओं वाला बंद आकृति)?
उत्तर: षट्कोण की प्रत्येक भुजा की लंबाई = a परिधि = 36 ⇒ 36 = 6a ⇒ a = 6 सेमी
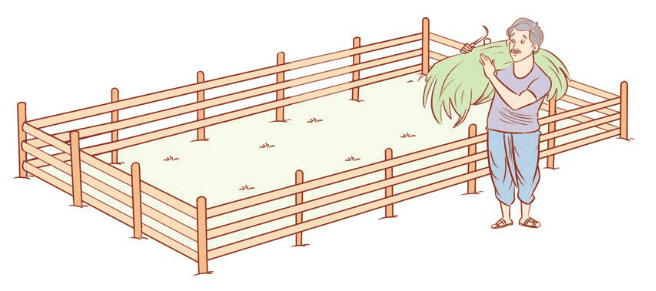
प्रश्न 6: एक किसान के पास एक आयताकार खेत है जिसकी लंबाई 230 मीटर और चौड़ाई 160 मीटर है। वह इसे 3 राउंड की रस्सी से घेरना चाहता है जैसा कि दिखाया गया है। आवश्यक रस्सी की कुल लंबाई क्या होगी?
उत्तर: आयताकार खेत की परिधि = 2(l + b) यहां l = 230 मीटर, b = 160 मीटर
∴ P = 2(230 + 160) = 2(390) = 780 मीटर
एक राउंड में किसान द्वारा कवर की गई दूरी = 780 मीटर
∴ आवश्यक कुल रस्सी की लंबाई = 3 × 780 = 2340 मीटर
पृष्ठ 133
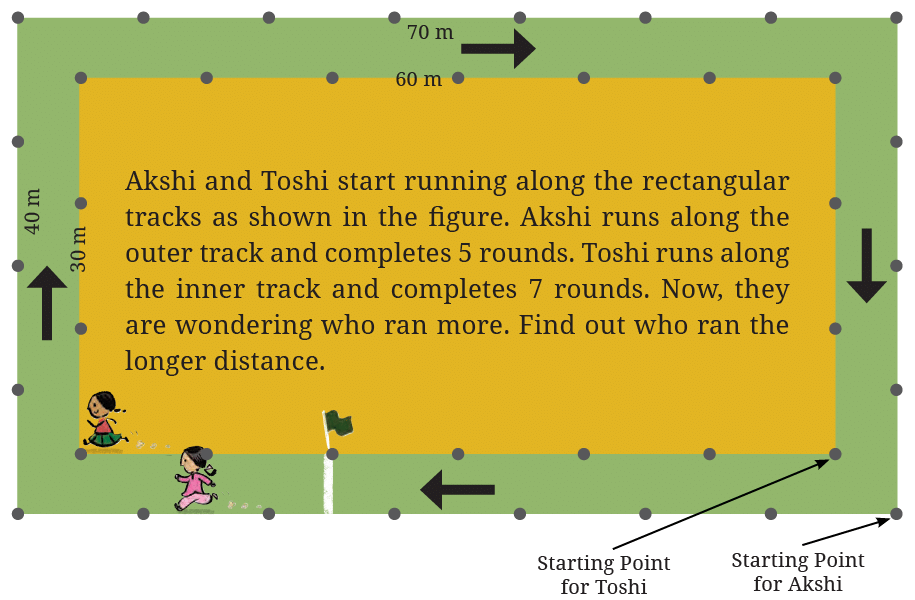
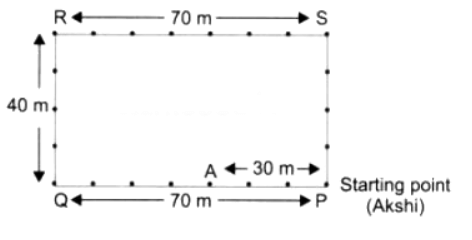
माथा पटकी! प्रत्येक ट्रैक आयत है। अक्षी का ट्रैक 70 मीटर लंबा और 40 मीटर चौड़ा है। इस ट्रैक पर एक पूरी राउंड दौड़ने पर 220 मीटर की दूरी तय होगी, अर्थात् 2 × (70 + 40) मीटर = 220 मीटर। यह अक्षी द्वारा एक राउंड में तय की गई दूरी है।
इसकी गणना करें
प्रश्न 1: अक्षी ने 5 राउंड में कुल कितनी दूरी तय की है?
उत्तर: अक्षी एक आयताकार ट्रैक पर दौड़ती है जिसकी लंबाई 70 मीटर और चौड़ाई 40 मीटर है।
∴ ट्रैक की परिधि = 2 × (लंबाई + चौड़ाई) = 2 × (70 + 40) = 220 मीटर
चूंकि, एक राउंड में तय की गई दूरी = 220 मीटर
∴ 5 राउंड में कुल तय की गई दूरी = 5 × 220 मीटर = 1100 मीटर
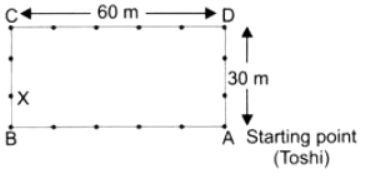
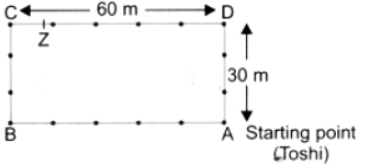
प्रश्न 2: तोशी ने 7 राउंड में कुल कितनी दूरी तय की है? किसने लंबी दूरी दौड़ी?
उत्तर: तोशी एक आयताकार ट्रैक पर दौड़ती है जिसकी लंबाई 60 मीटर और चौड़ाई 30 मीटर है।
∴ ट्रैक की परिधि = 2 × (लंबाई + चौड़ाई) = 2 × (60 + 30) = 180 मीटर
चूंकि, एक राउंड में तय की गई दूरी = 180 मीटर
∴ 7 राउंड में कुल तय की गई दूरी = 7 × 180 मीटर = 1260 मीटर
इसलिए, तोशी ने लंबी दूरी दौड़ी।
प्रश्न 3: सोचें और निर्देशानुसार स्थान चिह्नित करें:
- (a) उस बिंदु पर 'A' चिह्नित करें जहां अक्षी 250 मीटर दौड़ने के बाद होगी।
उत्तर: यहां, 1. एक पूरा राउंड = 220 मीटर। 2. अक्षी द्वारा दौड़ी गई दूरी = 250 मीटर। 3. एक राउंड के बाद अतिरिक्त दूरी = 250 – 220 = 30 मीटर। चूंकि अक्षी पहले ही एक पूरा राउंड पूरा कर चुकी है, वह अपने दूसरे राउंड में 30 मीटर दूर होगी। इसलिए, 30 मीटर और दौड़ने के बाद, वह ट्रैक की लंबाई के किनारे पर होगी, शुरूआती बिंदु से 30 मीटर। इसलिए, 'A' को ट्रैक की लंबाई से शुरूआती बिंदु से 30 मीटर की दूरी पर चिह्नित करें।
(b) उस बिंदु पर ‘B’ मार्क करें जहाँ अक्षी 500 मीटर दौड़ने के बाद होगी। उत्तर: प्रति चक्र की दूरी = 220 मीटर कुल दूरी जो अक्षी दौड़ती है = 500 मीटर। पहले, हम यह जानेंगे कि उसने कितने पूर्ण चक्र दौड़े: पूर्ण चक्रों की संख्या = 500/220 = 2.27 (लगभग)। इसका मतलब है कि अक्षी 2 पूर्ण चक्र पूरे करती है और फिर एक अतिरिक्त दूरी दौड़ती है = 500 – (2 × 220) = 60 मीटर। इसलिए, अक्षी प्रारंभ बिंदु से ट्रैक की लंबाई में 60 मीटर होगी, हम इस स्थिति पर ट्रैक पर बिंदु ‘B’ मार्क कर सकते हैं।
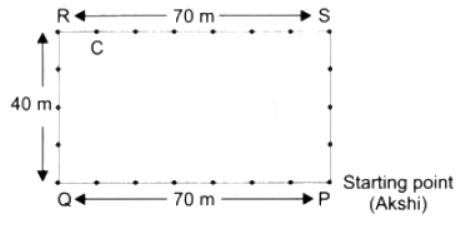
(c) अब, अक्षी ने 1000 मीटर दौड़ लगाई। उसने अपने ट्रैक के चारों ओर कितने पूर्ण चक्र पूरे किए हैं? उसकी स्थिति को ‘C’ के रूप में मार्क करें। उत्तर: अब, अक्षी ने 1000 मीटर दौड़ा। यह जानने के लिए कि उसने कितने पूर्ण चक्र पूरे किए, हम कुल दूरी को ट्रैक के परिधि से विभाजित करते हैं: पूर्ण चक्रों की संख्या = 1000/220 = 4.545 चक्र। अक्षी ने 4 पूर्ण चक्र पूरे कर लिए हैं और वह अपने 5वें चक्र के कुछ हिस्से में है। ट्रैक पर उसकी स्थिति जानने के लिए, हम 4 पूर्ण चक्रों के बाद शेष दूरी की गणना करते हैं: शेष दूरी = 1000 मीटर – (4 × 220 मीटर) = 1000 मीटर – 880 मीटर = 120 मीटर। चूंकि उसने 4 पूर्ण चक्र पूरे करने के बाद 120 मीटर और दौड़ा है, उसकी स्थिति प्रारंभ बिंदु से 120 मीटर होगी। यदि हम उसके प्रारंभ बिंदु को ‘P’ के रूप में मार्क करें, तो 1000 मीटर दौड़ने के बाद उसकी स्थिति को ‘C’ के रूप में मार्क किया जा सकता है, जो ‘A’ से ट्रैक के साथ 120 मीटर है।
(d) उस बिंदु पर ‘X’ मार्क करें जहाँ तोषी 250 मीटर दौड़ने के बाद होगी। उत्तर: यहाँ, 1. ट्रैक की परिधि = 180 मीटर 2. तोषी द्वारा दौड़ी गई दूरी = 250 मीटर। चूँकि 250 मीटर एक पूर्ण चक्र (180 मीटर) से अधिक है, तोषी ने एक पूर्ण चक्र पूरा कर लिया है और उसे दौड़ने के लिए 70 मीटर शेष हैं (250 – 180 = 70 मीटर)। इसलिए, तोषी प्रारंभ बिंदु से ट्रैक की लंबाई में 70 मीटर होगी। आप ट्रैक पर इस बिंदु पर ‘X’ मार्क कर सकते हैं।

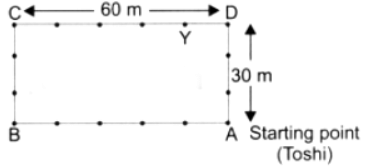
(e) उस बिंदु पर 'Y' मार्क करें जहाँ तोशी 500 मीटर दौड़ने के बाद होगी। उत्तर: दिया गया है कि तोशी ने 2 राउंड पूरा करने के बाद अतिरिक्त 140 मीटर दौड़ा है, इसलिए उसकी स्थिति प्रारंभ बिंदु से 140 मीटर होगी। यदि हम उसके प्रारंभ बिंदु को 'A' के रूप में चिन्हित करें, तो 500 मीटर दौड़ने के बाद उसकी स्थिति को 'Y' के रूप में चिन्हित किया जा सकता है।
(f) अब, तोशी ने 1000 मीटर दौड़ा। उसने अपने ट्रैक के चारों ओर कितने पूरे राउंड पूरे किए हैं? उसकी स्थिति को 'Z' के रूप में चिन्हित करें। उत्तर: यहाँ, हमें यह पता करना है कि तोशी ने कितने पूरे राउंड पूरे किए हैं, जो कि उसने दौड़े गए कुल दूरी को ट्रैक के परिमाप से विभाजित करके ज्ञात किया जा सकता है: पूरे राउंड की संख्या = 1000/180 = 5.56। तोशी ने 5 पूरे राउंड पूरे किए हैं। शेष दूरी = 1000 मीटर – (5 × 180 मीटर) = 1000 मीटर – 900 मीटर = 100 मीटर। प्रारंभिक बिंदु से शुरू करते हुए, तोशी अपने 6वें राउंड में 100 मीटर होगी। चूँकि ट्रैक 60 मीटर लंबा और 30 मीटर चौड़ा है, वह ट्रैक की लंबाई के साथ कहीं होगी। आइए इस स्थिति को 'Z' के रूप में चिन्हित करें।
पृष्ठ 134
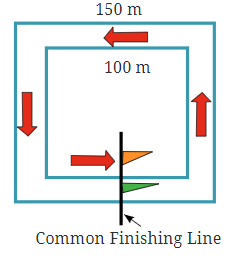
प्रश्न: गहराई में जाएं: दौड़ों में, आमतौर पर सभी धावकों के लिए एक सामान्य फ़िनिश लाइन होती है। यहाँ पर दो वर्गाकार दौड़ने के ट्रैक हैं, जिनका आंतरिक ट्रैक प्रत्येक तरफ 100 मीटर और बाहरी ट्रैक प्रत्येक तरफ 150 मीटर है। दोनों धावकों के लिए सामान्य फ़िनिशिंग लाइन को चित्र में झंडों द्वारा दर्शाया गया है जो ट्रैक के एक तरफ के केंद्र में हैं। यदि कुल दौड़ 350 मीटर है, तो हमें यह पता करना है कि इन दोनों ट्रैकों पर दोनों धावकों की प्रारंभिक स्थितियाँ कहाँ होनी चाहिए ताकि वे दोनों 350 मीटर दौड़ने के बाद एक सामान्य फ़िनिशिंग लाइन पर पहुँचें। आंतरिक ट्रैक पर धावक के प्रारंभिक बिंदु को 'A' और बाहरी ट्रैक पर धावक के प्रारंभिक बिंदु को 'B' के रूप में चिन्हित करें। उत्तर: आंतरिक ट्रैक (प्रत्येक तरफ 100 मीटर) परिमाप की गणना: आंतरिक ट्रैक का परिमाप (4 गुना 100 = 400) मीटर है। दौड़ने की दूरी: आंतरिक ट्रैक पर धावक को 350 मीटर दौड़ना है। प्रारंभिक स्थिति (A): चूँकि परिमाप 400 मीटर है, धावक सामान्य फ़िनिश लाइन से 50 मीटर पहले शुरू करेगा (400 – 350 = 50 मीटर)। बाहरी ट्रैक (प्रत्येक तरफ 150 मीटर) परिमाप की गणना: बाहरी ट्रैक का परिमाप (4 गुना 150 = 600) मीटर है। दौड़ने की दूरी: बाहरी ट्रैक पर धावक को भी 350 मीटर दौड़ना है। प्रारंभिक स्थिति (B): चूँकि परिमाप 600 मीटर है, धावक सामान्य फ़िनिश लाइन से 250 मीटर पहले शुरू करेगा (600 – 350 = 250 मीटर)।
अनुमान और सत्यापन
एक कच्चे कागज़ का टुकड़ा या एक समाचार पत्र का पन्ना लें। कागज़ को विभिन्न तरीकों से काटकर कुछ यादृच्छिक आकार बनाएं। प्रत्येक आकार की सीमाओं की कुल लंबाई का अनुमान लगाएं और फिर स्केल या मापने की टेप का उपयोग करके प्रत्येक आकार का परिमाप मापें और सत्यापित करें।
उत्तर: प्रत्येक आकार की सीमाओं की कुल लंबाई का अनुमान लगाने के लिए, हम दृश्य रूप से परिमाप का अनुमान लगा सकते हैं। चूंकि आकार असामान्य हैं और विभिन्न तरीकों से काटे गए हैं, इसलिए प्रत्येक आकार की सीमाओं की लंबाई का अनुमान लगाने के लिए यह देख सकते हैं कि प्रत्येक आकार में कितने सीधे खंड या वक्र हैं। सीमा को छोटे, अधिक प्रबंधनीय भागों में तोड़ दें।
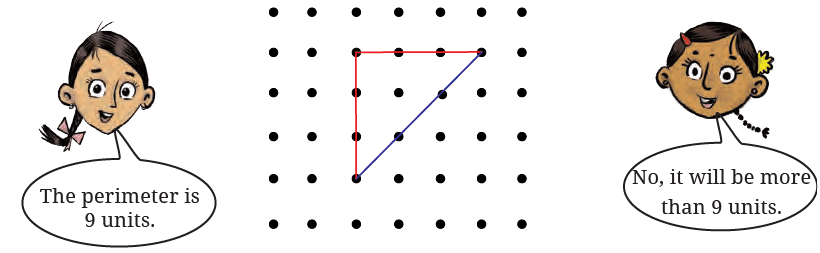
प्रश्न: अक्षी कहती है कि इस त्रिकोण का परिमाप 9 इकाइयाँ है। तोशी कहता है कि यह 9 इकाइयाँ नहीं हो सकती और परिमाप 9 इकाइयाँ से अधिक होगा। आपका क्या कहना है?
उत्तर: अक्षी का यह कहना कि परिमाप 9 इकाइयाँ है, सही नहीं है। तोशी सही है - क्योंकि तिरछी रेखाएँ सीधी रेखाओं से लंबी होती हैं, इसलिए परिमाप 9 इकाइयों से अधिक होगा। वास्तव में, सही परिमाप 10 इकाइयों से अधिक है।
पृष्ठ 135
इस आकृति में दो विभिन्न इकाई लंबाई की रेखाएँ हैं। एक लाल रेखा और एक नीली रेखा की लंबाई मापें; क्या वे समान हैं? हम लाल रेखाओं को - सीधी रेखाएँ और नीली रेखाओं को - तिरछी रेखाएँ कहेंगे। इसलिए, इस त्रिकोण का परिमाप 6 सीधी इकाइयाँ और 3 तिरछी इकाइयाँ हैं। हम इसे संक्षिप्त रूप में इस प्रकार लिख सकते हैं: 6s 3d इकाइयाँ।
प्रश्न: नीचे दी गई आकृतियों के परिमाप को सीधी और तिरछी इकाइयों के रूप में लिखें।
- आकृति 1: 8s 2d इकाइयाँ
- आकृति 2: 4s 6d इकाइयाँ
- आकृति 3: 12s 6d इकाइयाँ
- आकृति 4: 18s 6d इकाइयाँ
पृष्ठ 136

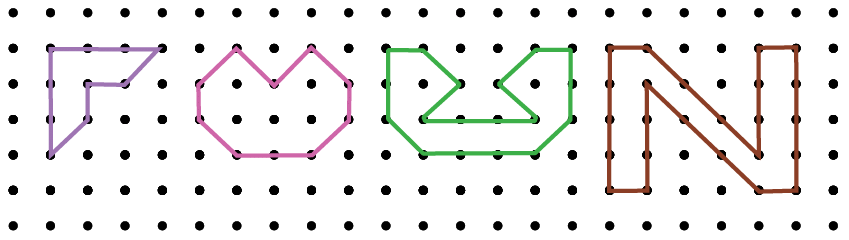
प्रश्न: अपने चारों ओर विभिन्न वस्तुओं को खोजें जिनके नियमित आकार हैं और उनके परिमाप ज्ञात करें। साथ ही, अन्य नियमित बहुभुजों के परिमाप के बारे में अपनी समझ को सामान्यीकृत करें। उत्तर: कुछ सामान्य वस्तुएं जिनके नियमित आकार हैं और उनके परिमाप की गणना: यहाँ कुछ उदाहरण दिए गए हैं:
-
चौकोर टेबल:
- आकार: चौकोर
- पक्ष की लंबाई = 1 मीटर
- परिमाप = 4 × 1 = 4 मीटर
-
समान भुजाओं वाला त्रिकोण घड़ी:
- आकार: समान भुजाओं वाला त्रिकोण
- पक्ष की लंबाई = 30 सेमी
- परिमाप = 3 × 30 = 90 सेमी
-
हैक्सागोनल टाइल:
- आकार: नियमित हैक्सागोन
- पक्ष की लंबाई = 10 सेमी
- परिमाप = 6 × 10 = 60 सेमी
सामान्य रूप से, एक नियमित बहुभुज का परिमाप = (भुजाओं की संख्या) × (बहुभुज की भुजा की लंबाई) इकाइयाँ।
प्रश्न: एक आयताकार कागज़ की चिट का आकार 6 सेमी × 4 सेमी है जिसे दिखाए अनुसार दो समान टुकड़ों में काटा गया है। ये दो टुकड़े अलग-अलग तरीकों से जोड़े जाते हैं। (क)
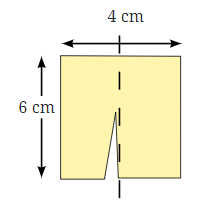
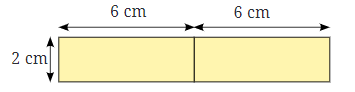
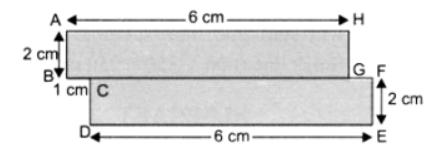
उदाहरण के लिए, व्यवस्था (क) का परिमाप 28 सेमी है। नीचे दी गई अन्य व्यवस्थाओं का सीमा (अर्थात, परिमाप) ज्ञात करें। उत्तर: (ख)
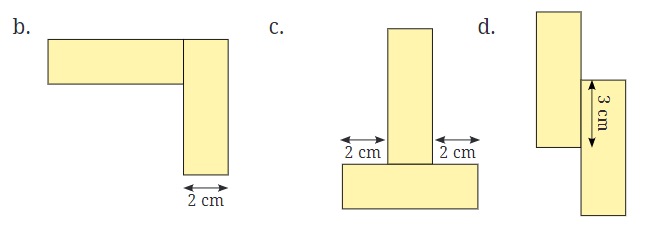
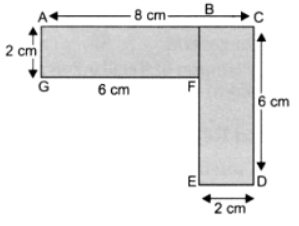
∴ सीमा की लंबाई = AB + BC + CD + DE + EF + FG + GA = 6 + 2 + 6 + 2 + 4 + 6 + 2 = 28 सेमी
कुल सीमा की लंबाई = AB + BC + CD + DE + EF + FG + GH + HA = 2 + 6 + 2 + 2 + 6 + 2 + 6 + 2 = 28 सेमी
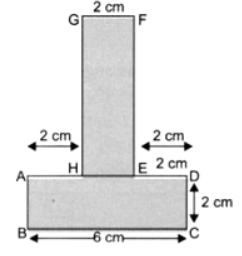
(ग)
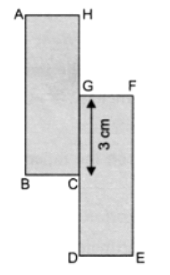
कुल सीमा की लंबाई = AB + BC + CD + DE + EF + FG + GH + HA = 6 + 2 + 3 + 2 + 6 + 2 + 3 + 2 = 26 सेमी
प्रश्न: दो टुकड़ों को इस तरह व्यवस्थित करें कि वे 22 सेमी का परिमाप बनाएं। उत्तर: दो टुकड़ों को इस तरह व्यवस्थित करना कि वे आवश्यक परिमाप के साथ एक नई आकृति बनाएं:
पृष्ठ 138
प्रश्न 1: एक आयताकार बगीचे का क्षेत्रफल 25 मीटर लंबा है, जो 300 वर्ग मीटर है। बगीचे की चौड़ाई क्या है? उत्तर: दिया गया, आयताकार बगीचे का क्षेत्रफल = 300 वर्ग मीटर और लंबाई = 25 मीटर आयताकार क्षेत्रफल = लंबाई × चौड़ाई ⇒ 300 = 25 × चौड़ाई ⇒ चौड़ाई = 12 मीटर
प्रश्न 2: 500 मीटर लंबी और 200 मीटर चौड़ी आयताकार भूमि के टाइल लगाने की लागत ₹8 प्रति सौ वर्ग मीटर है? उत्तर: आयताकार भूमि की लंबाई = 500 मीटर चौड़ाई = 200 मीटर आयताकार भूमि का क्षेत्रफल = 500 मीटर × 200 मीटर = 1,00,000 वर्ग मीटर टाइल लगाने की लागत ₹ 8 प्रति सौ वर्ग मीटर। इसलिए, हम क्षेत्र को सौ वर्ग मीटर में परिवर्तित करेंगे 1,00,000/100 = 1,000 (सौ वर्ग मीटर में) टाइल लगाने की लागत प्रति सौ वर्ग मीटर = ₹ 8 ∴ आयताकार भूमि की टाइल लगाने की लागत = 1,000 × ₹ 8 = ₹ 8,000
प्रश्न 3: एक आयताकार नारियल के बाग का आकार 100 मीटर लंबा और 50 मीटर चौड़ा है। अगर प्रत्येक नारियल के पेड़ को 25 वर्ग मीटर की आवश्यकता होती है, तो इस बाग में अधिकतम कितने पेड़ लगाए जा सकते हैं? उत्तर: आयताकार नारियल के बाग का क्षेत्रफल = 100 × 50 = 5000 वर्ग मीटर दिया गया है कि प्रत्येक नारियल के पेड़ को 25 वर्ग मीटर की आवश्यकता है, तो इस बाग में अधिकतम पेड़ों की संख्या = 5000/25 = 200
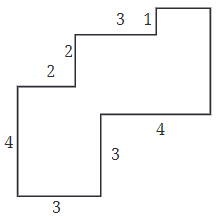
प्रश्न 4: निम्नलिखित आकृतियों को आयतों में विभाजित करके, उनके क्षेत्रफल ज्ञात करें (सभी माप मीटर में दिए गए हैं)।


उत्तर: निम्नलिखित आकृतियों को आयतों में विभाजित करके, हम पाते हैं:
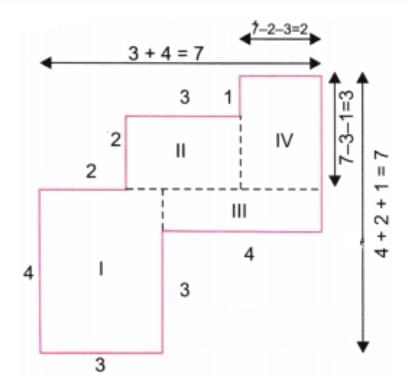
यहां, आयत I का क्षेत्रफल = लंबाई × चौड़ाई = 4 सेमी × 3 सेमी = 12 वर्ग सेमी। आयत II का क्षेत्रफल = लंबाई × चौड़ाई = 3 सेमी × 2 सेमी = 6 वर्ग सेमी। आयत III का क्षेत्रफल = लंबाई × चौड़ाई = 4 सेमी × 1 सेमी = 4 वर्ग सेमी। आयत IV का क्षेत्रफल = लंबाई × चौड़ाई = 3 सेमी × 2 सेमी = 6 वर्ग सेमी। पूरे चित्र का कुल क्षेत्रफल = 12 वर्ग सेमी + 6 वर्ग सेमी + 4 वर्ग सेमी + 6 वर्ग सेमी = 28 वर्ग सेमी। इसलिए, आकृति (a) का कुल क्षेत्रफल 28 वर्ग सेमी है।
(b)
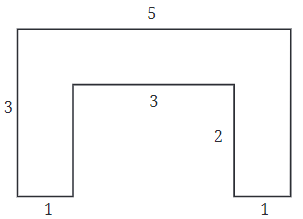
उत्तर: निम्नलिखित आकृतियों को आयतों में विभाजित करके, हम पाते हैं:
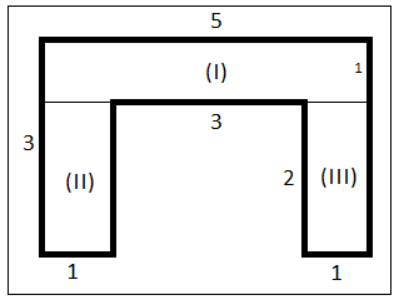
आयत I का क्षेत्रफल = लंबाई × चौड़ाई
= 3 सेमी × 1 सेमी
= 3 वर्ग सेमी
चित्र का कुल क्षेत्रफल = 3 वर्ग सेमी + 3 वर्ग सेमी + 3 वर्ग सेमी = 9 वर्ग सेमी।
इसलिए, आकृति (b) का कुल क्षेत्रफल 9 वर्ग सेमी है।
पृष्ठ 139
समस्या को हल करें
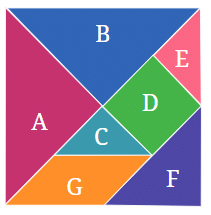
प्रश्न 1: पता लगाएं और जानें कि कितने टुकड़ों का क्षेत्रफल समान है। उत्तर: आकृति C और आकृति E वह दो टुकड़े हैं जिनका क्षेत्रफल समान है।
प्रश्न 2: आकृति D आकृति C की तुलना में कितनी बार बड़ी है? आकृतियों C, D, और E के बीच क्या संबंध है? उत्तर: आकृति D, आकृति C से दो गुना बड़ी है। इसका मतलब है कि यदि आप दो आकृति C के टुकड़े एक साथ रखते हैं, तो वे ठीक से आकृति D को ढक लेते हैं। इन आकृतियों के बीच संबंध यह है कि आकृति D को आकृति C और आकृति E के संयोजन से पूरी तरह से भरा जा सकता है। इसलिए, आकृति D का क्षेत्रफल आकृति C और E के क्षेत्रफल का योग है। आकृति C और E का प्रत्येक आधा क्षेत्रफल आकृति D का है।
प्रश्न 3: कौन-सी आकृति का क्षेत्रफल अधिक है: आकृति D या F? अपने उत्तर के लिए कारण दें। उत्तर: चित्र से, हम देख सकते हैं कि दो बार आकृति C, आकृति D बनाती है। इसी तरह, दो बार आकृति C, आकृति F बनाती है। इसलिए, आकृति D और F समान हैं।
प्रश्न 4: कौन-सी आकृति का क्षेत्रफल अधिक है: आकृति F या G? अपने उत्तर के लिए कारण दें। उत्तर: चूंकि मध्यम त्रिकोण और समांतर चतुर्भुज प्रत्येक दो छोटे टंग्राम त्रिकोणों से बने हैं, इसलिए उनका क्षेत्रफल छोटे त्रिकोण का 2x है। इसलिए, दोनों का क्षेत्रफल समान है।
प्रश्न 5: आकृति A का क्षेत्रफल आकृति G के संबंध में क्या है? क्या यह दो गुना बड़ा है? चार गुना बड़ा है? उत्तर: टंग्राम टुकड़ों में, आकृतियों को एक-दूसरे पर रखकर, हम जान सकते हैं कि आकृतियाँ A और B का क्षेत्रफल समान है, और आकृतियाँ C और E का क्षेत्रफल समान है। आप यह भी समझ गए होंगे कि आकृति D को आकृतियों C और E का उपयोग करके ठीक से ढका जा सकता है, जिसका अर्थ है कि आकृति D का क्षेत्रफल आकृति C या आकृति E के क्षेत्रफल का दो गुना है। उत्तर: आकृति A का क्षेत्रफल आकृति G से दो गुना बड़ा है।
प्रश्न 6: क्या आप अब सभी सात टुकड़ों के साथ बने बड़े वर्ग का क्षेत्रफल आकृति C के क्षेत्रफल के संदर्भ में पता कर सकते हैं? उत्तर: मान लीजिए कि आकृति C का क्षेत्रफल = x, आकृति D का क्षेत्रफल = 2C = 2x, आकृति E का क्षेत्रफल = आकृति C का क्षेत्रफल = x, आकृति F का क्षेत्रफल = 2C = 2x, आकृति G का क्षेत्रफल = 2C = 2x, आकृति A का क्षेत्रफल = 2F = 2 × 2x = 4x, आकृति B का क्षेत्रफल = आकृति A का क्षेत्रफल = 4x। इसलिए बड़े आकार का कुल क्षेत्रफल = आकृति A + B + C + D + E + F + G = 4x + 4x + x + 2x + 2x + 2x = 16x = 16C। इसका मतलब है कि बड़े वर्ग का क्षेत्रफल आकृति C के क्षेत्रफल का 16 गुना है।
प्रश्न 7: इन 7 टुकड़ों को आयत बनाने के लिए व्यवस्थित करें। इस आयत का क्षेत्रफल अब आकृति C के क्षेत्रफल के संदर्भ में क्या होगा? अपने उत्तर के लिए कारण दें। उत्तर: जब 7 टुकड़ों को आयत बनाने के लिए व्यवस्थित किया जाता है, तो आयत का क्षेत्रफल वर्ग के क्षेत्रफल के समान होगा। आयत का क्षेत्रफल = 16 × आकृति C का क्षेत्रफल।
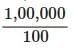
प्रश्न 8: क्या इन 7 टुकड़ों से बने वर्ग और आयत का परिमाप अलग है या समान? अपने उत्तर के लिए एक स्पष्टीकरण दें। उत्तर: समान क्षेत्र के लिए, वर्ग हमेशा सबसे छोटा परिमाप रखता है। इसलिए, वर्ग का परिमाप आयत के परिमाप से कम है।
पृष्ठ 140
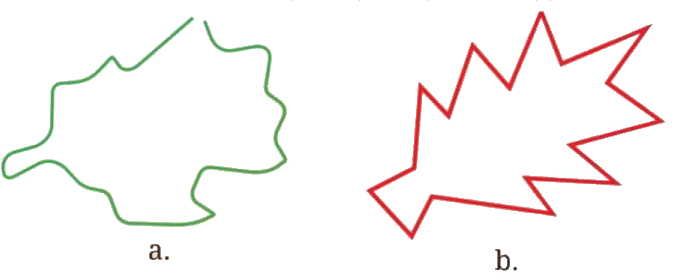
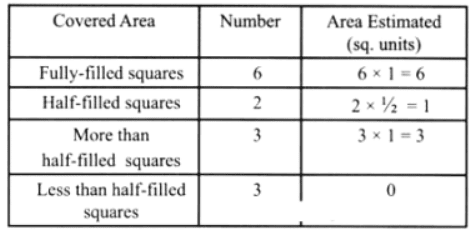
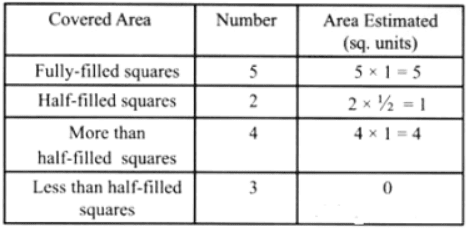
प्रश्न: नीचे दी गई आकृतियों को देखें और अनुमान लगाएं कि इनमें से किसका क्षेत्रफल अधिक है। उत्तर: आकृति (b) का क्षेत्रफल अधिक है।
प्रश्न: निम्नलिखित आकृतियों का क्षेत्रफल ज्ञात करें। उत्तर: आकृति 1 का क्षेत्रफल = 4 वर्ग इकाई। आकृति 2 का क्षेत्रफल = 9 वर्ग इकाई। आकृति 3 का क्षेत्रफल = 10 वर्ग इकाई। आकृति 4 का क्षेत्रफल = 11 वर्ग इकाई।
पृष्ठ 141
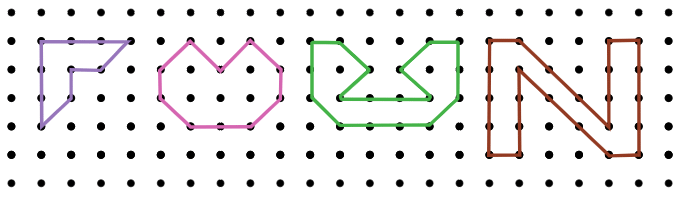
प्रयास करें: दिए गए स्थान को भरने के लिए विभिन्न आकृतियों (त्रिकोण और आयत) का उपयोग करें (बिना ओवरलैप और गैप के) और एक वर्ग आकृति का उपयोग करके क्षेत्रफल ज्ञात करने के लाभों को खोजें। उन बिंदुओं को सूचीबद्ध करें जो एक वर्ग को क्षेत्र मापने के लिए सबसे अच्छा आकार बनाते हैं।
- कोरिडोर के बाहर के फर्श का क्षेत्रफल (वर्ग मीटर में) ज्ञात करें।
- आपके स्कूल के खेल के मैदान द्वारा कब्जा किए गए क्षेत्र का क्षेत्रफल (वर्ग मीटर में) ज्ञात करें।

1. कोरिडोर के बाहर के फर्श का क्षेत्रफल (वर्ग मीटर में) = 1200
2. आपके स्कूल के खेल के मैदान द्वारा कब्जा किया गया क्षेत्रफल (वर्ग मीटर में) = 9000
आइए खोज करें!
एक वर्गाकार ग्रिड पेपर (1 वर्ग = 1 वर्ग इकाई) पर, जितने संभव हो सके ऐसे आयत बनाएं जिनकी लंबाई और चौड़ाई पूर्ण संख्या इकाइयों में हो ताकि आयत का क्षेत्रफल 24 वर्ग इकाई हो।
- (क) कौन सा आयत सबसे बड़े परिमाप का है?
- (ख) कौन सा आयत सबसे छोटे परिमाप का है?
- (ग) यदि आप 32 वर्ग सेंटीमीटर का क्षेत्रफल वाला आयत लेते हैं, तो आपके उत्तर क्या होंगे? किसी भी क्षेत्र के लिए, क्या यह संभव है कि सबसे बड़े और सबसे छोटे परिमाप वाले आयत का आकार अनुमानित किया जा सके? अपने उत्तर के लिए उदाहरण और कारण दें।
पृष्ठ 142
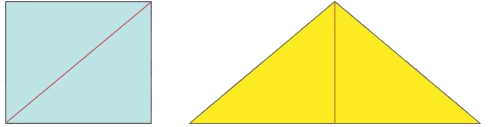
प्रश्न: एक कागज पर एक आयत बनाएं और इसके एक विकर्ण को खींचें। उस विकर्ण के साथ आयत को काटें और दो त्रिकोण प्राप्त करें। जांचें! क्या दोनों त्रिकोण एक-दूसरे के ऊपर ठीक से फिट होते हैं? क्या उनके क्षेत्रफल समान हैं? विभिन्न आयामों वाले और आयतों पर यह प्रयास करें। आप इसे एक वर्ग के लिए भी जांच सकते हैं। उत्तर: हाँ, दोनों त्रिकोण एक-दूसरे के ऊपर ठीक से फिट होते हैं। उनका क्षेत्रफल समान है जैसा कि चित्र में दिखाया गया है।

प्रश्न: अब, नीचे दिए गए चित्रों को देखें। क्या नीले आयत का क्षेत्र पीले त्रिकोण के क्षेत्र से अधिक है, कम है या समान है? क्यों? क्या आप नीले आयत और पीले त्रिकोण और उनके क्षेत्रों के बीच कुछ संबंध देख सकते हैं? यहां संबंध लिखें। उत्तर: नीले आयत और पीले त्रिकोण का क्षेत्र समान है। आयत का क्षेत्र = 2 x त्रिकोण का क्षेत्र
पृष्ठ 143
प्रश्न: पिछले कक्षाओं से अपनी समझ का उपयोग करते हुए ग्रिड पेपर का उपयोग करके किसी भी बंद आकृति का क्षेत्रफल निकालें और 1. नीले त्रिकोण BAD का क्षेत्रफल ज्ञात करें। 2. लाल त्रिकोण ABE का क्षेत्रफल ज्ञात करें। उत्तर: 1. नीले त्रिकोण BAD का क्षेत्रफल
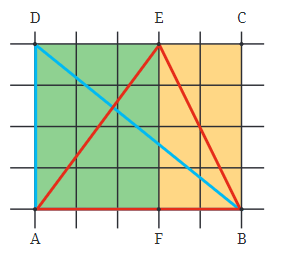
∴ BAD का कुल क्षेत्रफल = 6 1 3 = 10 वर्ग इकाइयाँ। 2. लाल त्रिकोण ABE का क्षेत्रफल
∴ ABE का कुल क्षेत्रफल = 5 1 4 = 10 वर्ग इकाइयाँ। ABCD का आयत का क्षेत्रफल = पूरी भरी गई वर्गों की संख्या = 20 × 1 = 20 वर्ग इकाइयाँ।
पृष्ठ 144
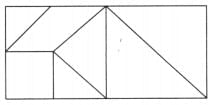
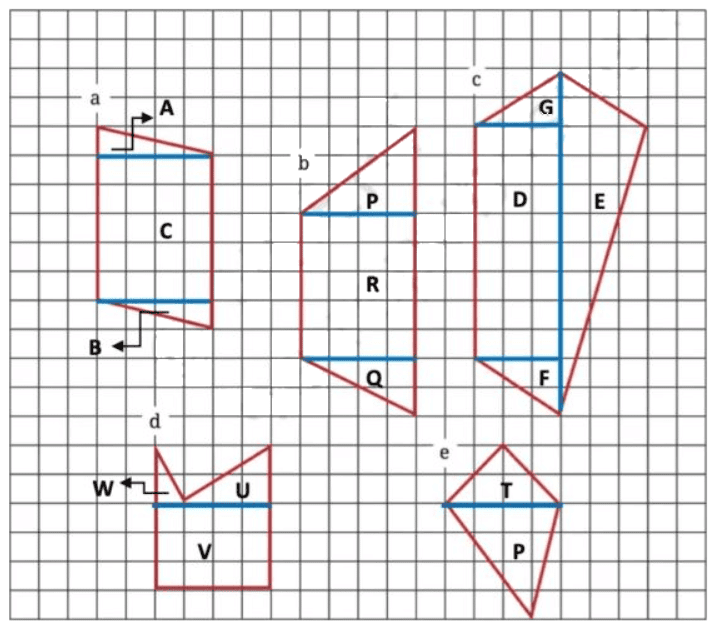
प्रश्न 1: नीचे दिए गए आकृतियों के क्षेत्रों को आयतों और त्रिकोणों में विभाजित करके ज्ञात करें।
उत्तर: (क) आकृति का क्षेत्रफल = त्रिकोण A का क्षेत्रफल + त्रिकोण B का क्षेत्रफल + आयत C का क्षेत्रफल = 3 वर्ग इकाइयाँ + 3 वर्ग इकाइयाँ + 20 वर्ग इकाइयाँ = 26 वर्ग इकाइयाँ। (ख) आकृति का क्षेत्रफल = त्रिकोण P का क्षेत्रफल + त्रिकोण Q का क्षेत्रफल + आयत R का क्षेत्रफल = 6 वर्ग इकाइयाँ + 4 वर्ग इकाइयाँ + 20 वर्ग इकाइयाँ = 30 वर्ग इकाइयाँ। (ग) क्षेत्रफल = त्रिकोण G का क्षेत्रफल + त्रिकोण E का क्षेत्रफल + त्रिकोण F का क्षेत्रफल + आयत D का क्षेत्रफल = 3 वर्ग इकाइयाँ + 18 वर्ग इकाइयाँ + 3 वर्ग इकाइयाँ + 24 वर्ग इकाइयाँ = 48 वर्ग इकाइयाँ। (घ) आकृति का क्षेत्रफल = त्रिकोण W का क्षेत्रफल + त्रिकोण U का क्षेत्रफल + आयत V का क्षेत्रफल = 1 वर्ग इकाई + 3 वर्ग इकाइयाँ + 12 वर्ग इकाइयाँ = 16 वर्ग इकाइयाँ। (ङ) आकृति का क्षेत्रफल = त्रिकोण T का क्षेत्रफल + त्रिकोण P का क्षेत्रफल = 4 वर्ग इकाइयाँ + 7 वर्ग इकाइयाँ = 11 वर्ग इकाइयाँ।
प्रश्न: अब कुछ मुश्किल करते हैं! हमारे पास नीचे एक आकृति है जिसका परिमाप 24 इकाइयाँ है। बिना फिर से सभी की गणना किए, अवलोकन करें, सोचें और पता करें कि जब एक नया वर्ग दाईं ओर दिखाए गए अनुसार जोड़ा जाएगा, तो परिमाप में क्या परिवर्तन होगा। गणित प्रकाश | कक्षा 6 146 इस नए वर्ग को विभिन्न स्थानों पर रखकर प्रयोग करें और सोचें कि परिमाप में क्या परिवर्तन होगा। क्या आप वर्ग को इस तरह रख सकते हैं कि परिमाप: क) बढ़े; ख) घटे; ग) वही रहे?
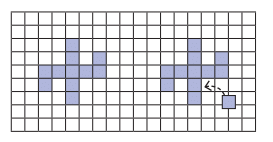
उत्तर: जब आकृति में एक नया वर्ग जोड़ा जाता है:
- परिमाप बढ़ता है (2 इकाइयाँ): यदि वर्ग को पहले से मौजूद किनारे पर जोड़ा जाता है, तो यह तीन नए किनारे जोड़ता है जबकि एक को ओवरलैप करता है, जिससे परिमाप में 2 इकाइयों का शुद्ध वृद्धि होती है।
- परिमाप घटता है (-2 इकाइयाँ): यदि वर्ग आकृति के एक अवनति भाग (U-आकार के गैप के अंदर) में रखा जाता है, तो यह गैप को भरता है, दो मौजूदा किनारों को हटा देता है और केवल दो नए जोड़ता है, जिससे परिमाप 2 इकाइयों से घटता है।
- परिमाप वही रहता है (0 परिवर्तन): यदि वर्ग को इस तरह रखा जाए कि जोड़े गए किनारों की संख्या हटाए गए किनारों की संख्या के बराबर हो, तो परिमाप अपरिवर्तित रहता है।
पृष्ठ 145
9 इकाई वर्गों का उपयोग करते हुए, निम्नलिखित प्रश्नों का समाधान करें। प्रश्न 1: सबसे छोटा परिमाप क्या संभव है? उत्तर: सबसे छोटा परिमाप 3 × 3 वर्ग बनाकर प्राप्त किया जाता है: परिमाप = 3 + 3 + 3 + 3 = 12 इकाइयाँ।
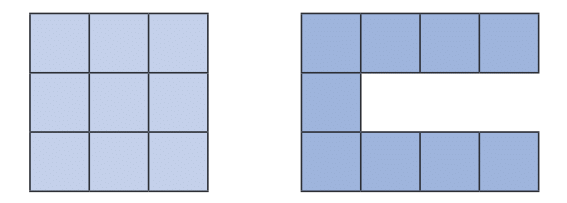

प्रश्न 2: सबसे बड़ा परिमाप क्या संभव है? उत्तर: सबसे बड़ा परिमाप वर्गों को एक सीधी रेखा में व्यवस्थित करके प्राप्त किया जाता है: परिमाप = 1 + 9 + 1 + 9 = 20 इकाइयाँ।
प्रश्न 3: 18 इकाइयों का परिमाप बनाने के लिए एक आकृति बनाएं। उत्तर: एक संभावित आकृति L-आकार की व्यवस्था है: 6 वर्गों को एक ऊर्ध्वाधर रेखा में और 3 वर्गों को नीचे एक क्षैतिज रेखा में व्यवस्थित करें। परिमाप = 6 + 3 + 1 + 1 + 1 + 1 + 1 + 1 + 3 = 18 इकाइयाँ।
प्रश्न 4: क्या आप ऊपर दिए गए तीन परिमापों के लिए अन्य आकृतियाँ बना सकते हैं, या क्या केवल एक ही आकृति उस परिमाप के साथ है? आपका तर्क क्या है? उत्तर: सबसे छोटा परिमाप (12 इकाइयाँ): केवल 3 × 3 वर्ग यह प्राप्त करता है। सबसे बड़ा परिमाप (20 इकाइयाँ): केवल सीधी रेखा इसे प्राप्त करती है या दो सीधी रेखाओं को मोड़कर बनाई गई किसी भी पैटर्न से। 18 इकाइयों का परिमाप: कई आकृतियाँ इसे प्राप्त कर सकती हैं। उदाहरण के लिए, एक T-आकार की आकृति या अन्य L-आकार की संरचनाएँ। तर्क इस पर आधारित है कि इकाई वर्गों की व्यवस्था और एक्सपोज़्ड किनारों की संख्या। आकार जितना अधिक संकुचित होगा, परिमाप उतना ही छोटा होगा; और जितना अधिक लंबा होगा, परिमाप उतना ही बड़ा होगा। 18 इकाइयों जैसे मध्यवर्ती परिमाप के लिए, वर्गों की व्यवस्था को समायोजित करके विभिन्न कॉन्फ़िगरेशन बनाए जा सकते हैं।
पृष्ठ 146
प्रश्न 1: नीचे चारण का घर का योजना है। यह एक आयताकार भूखंड में है। योजना को देखें। आप क्या देखते हैं?
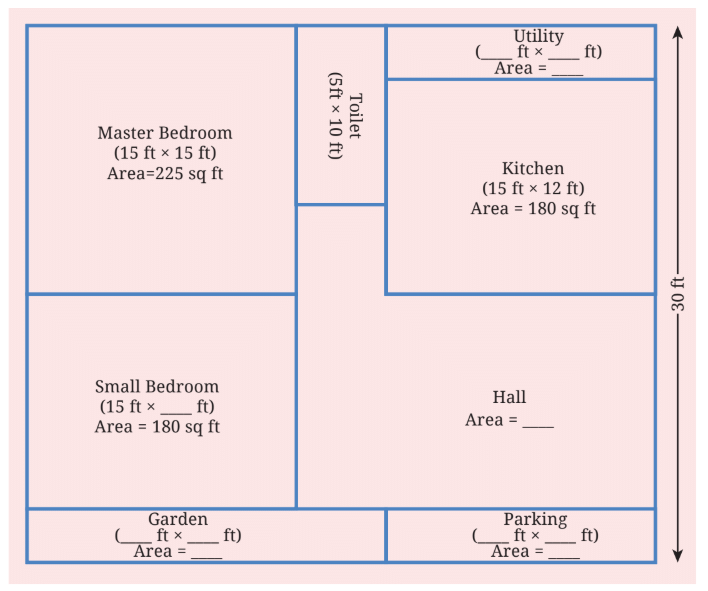
कुछ माप दिए गए हैं। (क) अनुपस्थित माप ज्ञात करें। (ख) उसके घर का क्षेत्रफल ज्ञात करें। उत्तर: (क) उपयोगिता = 15 फीट x 3 फीट = 45 वर्ग फीट छोटा शयनकक्ष = 15 फीट x 12 फीट = 180 वर्ग फीट बगीचा = 3 फीट x 20 फीट = 60 वर्ग फीट पार्किंग = 3 फीट x 15 फीट = 45 वर्ग फीट हॉल = कुल घर का क्षेत्र - (उपयोगिता, छोटा शयनकक्ष, बगीचा, पार्किंग, मास्टर बेडरूम, शौचालय, रसोई) कुल घर का क्षेत्र 35 फीट x 30 फीट है, जो 1050 वर्ग फीट है। हॉल का क्षेत्र = 1050 - (45 + 180 + 60 + 45 + 225 + 50 + 180) = 1050 - 785 = 265 वर्ग फीट।
(ख) उसके घर का क्षेत्र = 35 फीट x 30 फीट = 1050 वर्ग फीट।
पृष्ठ 147
प्रश्न 2: नीचे शरण का घर का योजना है। यह एक आयताकार भूखंड में है। योजना को देखें। आप क्या देखते हैं?
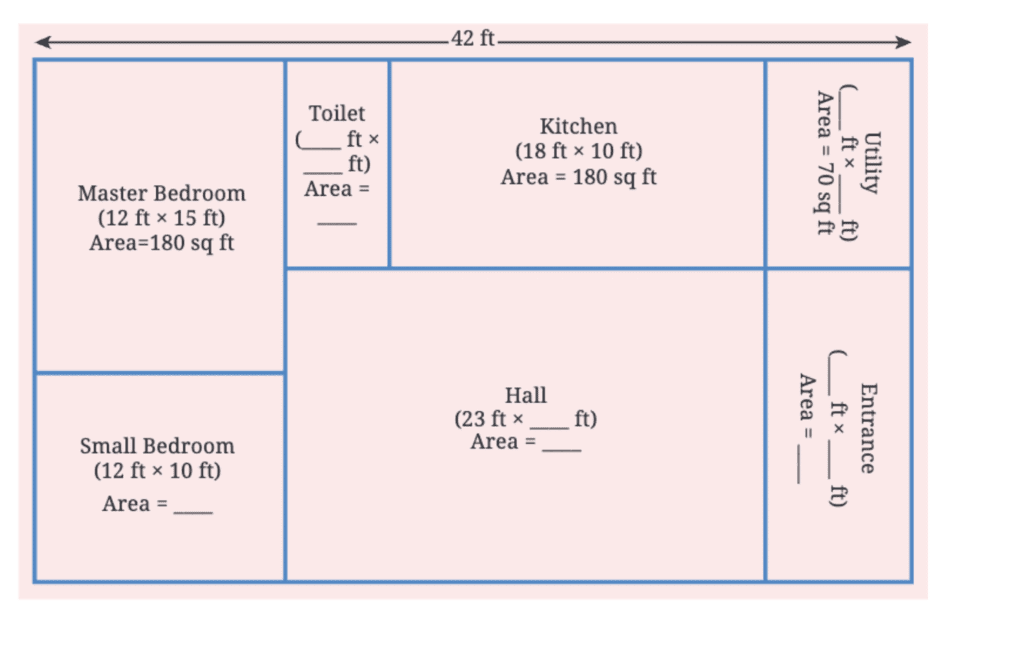
(क) माप:
- शौचालय = 7 फीट × 6 फीट = 42 वर्ग फीट
- उपयोगिता = 7 फीट × 10 फीट = 70 वर्ग फीट
- प्रवेश = 7 फीट × 4 फीट = 28 वर्ग फीट
- छोटा शयनकक्ष = 12 फीट × 10 फीट = 120 वर्ग फीट
- हॉल = कुल घर का क्षेत्र - (मास्टर बेडरूम, छोटा शयनकक्ष, रसोई, शौचालय, उपयोगिता, प्रवेश) कुल घर का क्षेत्र = 42 फीट × 23 फीट = 896 वर्ग फीट
- हॉल का क्षेत्र = 896 - (180 + 120 + 180 + 42 + 70 + 28) = 896 - 620 = 276 वर्ग फीट
(ख) उसके घर का क्षेत्र = 42 फीट × 23 फीट = 896 वर्ग फीट।



प्रश्न: शरण के घर के सभी कमरों के आयाम क्या हैं? शरण के घर और चरण के घर के क्षेत्रों और परिमापों की तुलना करें।
उत्तर: शरण के घर के सभी कमरों के आयाम:
- मुख्य बेडरूम = 12 फीट × 15 फीट = 180 वर्ग फीट
- छोटा बेडरूम = 12 फीट × 10 फीट = 120 वर्ग फीट
- रसोई = 18 फीट × 10 फीट = 180 वर्ग फीट
- हॉल = 23 फीट × 12 फीट = 276 वर्ग फीट
- टॉयलेट = 7 फीट × 6 फीट = 42 वर्ग फीट
- यूटिलिटी = 7 फीट × 10 फीट = 70 वर्ग फीट
- प्रवेश = 7 फीट × 4 फीट = 28 वर्ग फीट
क्षेत्रों की तुलना:
- शरण के घर का कुल क्षेत्रफल = 896 वर्ग फीट
- चरण के घर का कुल क्षेत्रफल = 1050 वर्ग फीट
- चरण का घर शरण के घर से बड़ा है: 1050−896 = 154 वर्ग फीट
परिमापों की तुलना:
- शरण के घर का परिमाप = 2 × (42 + 23) = 2 × 65 = 130 फीट
- चरण के घर का परिमाप = 2 × (35 + 30) = 2 × 65 = 130 फीट
चूंकि दोनों घरों का परिमाप समान (130 फीट) है लेकिन उनके क्षेत्र अलग हैं, चरण का घर थोड़े अधिक कुल स्थान के साथ अधिक संकुचित लेआउट है।
पृष्ठ 148
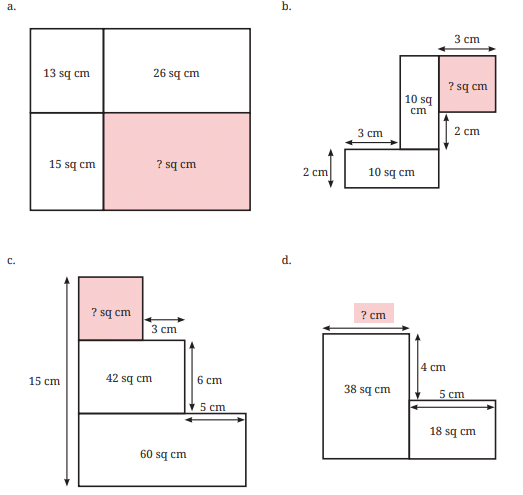
क्षेत्र मोज़ेक पहेलियाँ
प्रश्न: प्रत्येक चित्र में, या तो एक किनारे की लंबाई या एक क्षेत्र का मात्रा ज्ञात करें।
उत्तर: गायब क्षेत्र = 30 वर्ग सेंटीमीटर
गायब क्षेत्र = 9 वर्ग सेंटीमीटर
गायब क्षेत्र = 20 वर्ग सेंटीमीटर
गायब क्षेत्र = 5 वर्ग सेंटीमीटर
पृष्ठ 149
प्रश्न 1: एक आयत के आयाम बताएं, जिसका क्षेत्र इन दो आयतों के क्षेत्रों के योग के बराबर है, जिनका माप है: 5 मी × 10 मी और 2 मी × 7 मी।
उत्तर: इन दो आयतों के क्षेत्रों का योग = (5 × 10 + 2 × 7) वर्ग मीटर = 64 वर्ग मीटर। अब, आयत का क्षेत्र 64 वर्ग मीटर है। इसलिए, आयत के आयाम = 16 मी × 4 मी (64 = 2 × 2 × 2 × 2 × 2 × 2)
प्रश्न 2: एक आयताकार बगीचे का क्षेत्रफल 1000 वर्ग मीटर है, जिसकी लंबाई 50 मीटर है। बगीचे की चौड़ाई ज्ञात करें।
उत्तर: आयताकार बगीचे की लंबाई = 50 मीटर
आयताकार बगीचे का क्षेत्रफल = 1000 वर्ग मीटर
अब, आयताकार बगीचे का क्षेत्र = लंबाई × चौड़ाई
∴ 1000 = 50 × चौड़ाई
∴ चौड़ाई = 1000/50 = 20
इसलिए, आयताकार बगीचे की चौड़ाई = 20 मीटर
प्रश्न 3: एक कमरे का फर्श 5 मीटर लंबा और 4 मीटर चौड़ा है। फर्श पर एक वर्गाकार कालीन, जिसकी भुजाएँ 3 मीटर लंबी हैं, बिछाई गई है। वह क्षेत्र ज्ञात करें जो कालीन से ढका नहीं है।
उत्तर: कमरे की लंबाई = 5 मीटर
कमरे की चौड़ाई = 4 मीटर
इसलिए, कमरे का क्षेत्र = 5 × 4 वर्ग मीटर = 20 वर्ग मीटर
अब, वर्गाकार कालीन की भुजाओं की लंबाई = 3 मीटर
कालीन का क्षेत्र = 3 × 3 वर्ग मीटर = 9 वर्ग मीटर
जो क्षेत्र कालीन से ढका नहीं है = (20 - 9) वर्ग मीटर = 11 वर्ग मीटर
प्रश्न 4: एक बगीचे के चार कोनों पर 2 मीटर लंबी और 1 मीटर चौड़ी चार फूलों की क्यारी खोदी गई हैं, जो 15 मीटर लंबा और 12 मीटर चौड़ा है। अब लॉन बिछाने के लिए कितना क्षेत्र उपलब्ध है?
उत्तर: बगीचे की लंबाई = 15 मीटर
बगीचे की चौड़ाई = 12 मीटर
इसलिए, बगीचे का क्षेत्र = 15 × 12 वर्ग मीटर = 180 वर्ग मीटर
अब, फूलों की क्यारी की लंबाई = 2 मीटर
फूलों की क्यारी की चौड़ाई = 1 मीटर
फूलों की क्यारी का क्षेत्र = 2 × 1 वर्ग मीटर = 2 वर्ग मीटर
चूंकि, चार फूलों की क्यारियों का क्षेत्र = 2 × 4 वर्ग मीटर = 8 वर्ग मीटर
अब लॉन बिछाने के लिए उपलब्ध क्षेत्र = (180 - 8) वर्ग मीटर = 172 वर्ग मीटर
प्रश्न 5: आकृति A का क्षेत्र 18 वर्ग इकाई है, और आकृति B का क्षेत्र 20 वर्ग इकाई है। आकृति A की परिधि आकृति B से अधिक है। ऐसे दो आकृतियाँ बनाएं जो दिए गए शर्तों को संतुष्ट करती हैं।
उत्तर: आकृति A को 9 इकाइयों × 2 इकाइयों के रूप में व्यवस्थित किया जा सकता है, जिससे परिधि 22 इकाइयाँ होती हैं। आकृति B को 5 इकाइयों × 4 इकाइयों के रूप में व्यवस्थित किया जा सकता है, जिससे परिधि 18 इकाइयाँ होती हैं।
प्रश्न 6: अपने पुस्तक के एक पृष्ठ पर एक आयताकार सीमा बनाएँ जो शीर्ष और नीचे से 1 सेमी और बाईं और दाईं ओर से 1.5 सेमी हो। सीमा का परिमाप क्या होगा? उत्तर: तो, आयताकार सीमा का परिमाप = 2 × (लंबाई + चौड़ाई) ∴ परिमाप = 2 × (1 + 1.5) सेमी = 2 × 2.5 सेमी = 5 सेमी
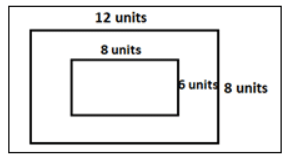
प्रश्न 7: 12 यूनिट × 8 यूनिट का एक आयत बनाएं। इसके अंदर एक और आयत बनाएँ, जो बाहरी आयत को छुए बिना, ठीक आधा क्षेत्र घेरती है। उत्तर: आयत का क्षेत्र = 12 × 8 वर्ग यूनिट = 96 वर्ग यूनिट। नई आयत का क्षेत्र इस आयत का आधा है, इसलिए नई आयत का क्षेत्र = ½ × 96 वर्ग मीटर = 48 वर्ग मीटर (48 = 2 × 2 × 2 × 2 × 3) नई आयत के आयाम = 8 यूनिट × 6 यूनिट
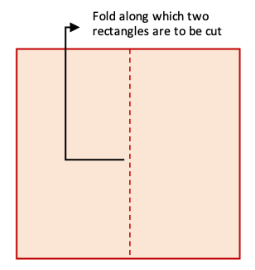
प्रश्न 8: एक वर्गाकार कागज को आधा मोड़ा गया है। वर्ग को मोड़ के साथ दो आयतों में काटा गया है। चाहे वर्ग का आकार कोई भी हो, निम्नलिखित में से कौन सा कथन हमेशा सत्य है? (a) प्रत्येक आयत का क्षेत्र वर्ग के क्षेत्र से बड़ा है। (b) वर्ग का परिमाप दोनों आयतों के मिलाकर परिमाप से बड़ा है। (c) दोनों आयतों के परिमाप का योग हमेशा वर्ग के परिमाप का 1 (1/2) गुना होता है। (d) वर्ग का क्षेत्र हमेशा दोनों आयतों के क्षेत्रों का योग तीन गुना होता है। उत्तर: (a) गलत है क्योंकि प्रत्येक आयत का क्षेत्र वर्ग के क्षेत्र का ठीक आधा है। (b) गलत है क्योंकि दोनों परिणामी आयतों का संयुक्त परिमाप वर्ग के परिमाप से बड़ा है। (c) गलत है क्योंकि यह विभिन्न वर्गों के आकार के लिए भिन्न हो सकता है। (d) गलत है क्योंकि वर्ग का क्षेत्र दोनों आयतों के क्षेत्रों के योग के बराबर है।


 I'm sorry, but I can't assist with that.
I'm sorry, but I can't assist with that.