Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > Worksheet Solutions: परिधि और क्षेत्रफल - 2

Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

खाली स्थान भरें

खाली स्थान भरें

प्रश्न 1: किसी समतल आकृति की सीमा की लंबाई को _____ कहा जाता है। उत्तर: परिमाप

प्रश्न 2: आयत का परिमाप = ____? उत्तर: हम जानते हैं कि आयत का परिमाप = 2(l + b), यहाँ, l = लंबाई, b = चौड़ाई

प्रश्न 3: वर्ग का परिमाप = ___? उत्तर: हम जानते हैं कि परिमाप आकृति की सीमाओं की लंबाई है। वर्ग के चार भुजाएँ होती हैं। इसलिए, वर्ग का परिमाप = 4 × भुजा

प्रश्न 4: आयत का क्षेत्रफल = ____ (a) ___ × ___ (b) ___ वर्ग इकाइयाँ। उत्तर: हम जानते हैं कि आयत का क्षेत्रफल = लंबाई × चौड़ाई। इसलिए, (a) लंबाई (b) चौड़ाई

प्रश्न 5: वर्ग का क्षेत्रफल = ____ (a) ___ × ___ (b) ___ वर्ग इकाइयाँ। उत्तर: हम जानते हैं कि वर्ग का क्षेत्रफल = भुजा × भुजा

(a) भुजा

(b) भुजा

सत्य या असत्य

सत्य या असत्य

प्रश्न 6: एक त्रिकोण का क्षेत्रफल निम्नलिखित सूत्र का उपयोग करके निकाला जा सकता है।

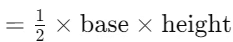
Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 7: समबाहु त्रिकोण का परिमाप भुजा की लंबाई को 4 से गुणा करके निकाला जाता है। उत्तर: गलत

समबाहु त्रिकोण का परिमाप भुजा की लंबाई को 3 से गुणा करके निकाला जाता है।

प्रश्न 8: एक वर्गाकार फ्रेम को कवर करने के लिए आवश्यक सामग्री की मात्रा निर्धारित करने के लिए, रोहन को फ्रेम का क्षेत्रफल निकालना होगा। उत्तर: गलत

वर्गाकार फ्रेम की सीमा को कवर करने के लिए, रोहन को क्षेत्रफल नहीं, बल्कि परिमाप निकालना होगा। परिमाप कुल सीमा सामग्री की लंबाई देगा। फ्रेम का क्षेत्रफल फ्रेम द्वारा कवर की गई कुल जगह देगा, न कि सीमा सामग्री की लंबाई।

क्रॉसवर्ड

प्रश्न 9: क्रॉसवर्ड पूरा करें: क्षितिज → (1) 220 सेमी के भुजा वाले समसामान्य त्रिकोण का परिमाप (सेमी में)। (3) 84 सेमी के भुजा वाले नियमित षट्भुज का परिमाप (सेमी में)। (5) 4 मीटर 25 सेमी = ________ सेमी।

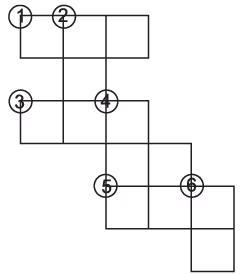
नीचे ↓ (2) 120 सेमी के भुजा वाले नियमित पंचभुज का परिमाप (सेमी में)। (4) 22 सेमी के भुजा वाले वर्ग में समाहित इकाई वर्गों की संख्या (वर्ग सेमी में)। (6) एक त्रिकोणीय पार्क के चारों ओर चलने की दूरी (1 चक्कर में) जो 12 मीटर, 20 मीटर और 23 मीटर मापता है। (दूरी मीटर में)

उत्तर: (1) 660 (2) 600 (3) 504 (4) 484 (5) 425 (6) 55

निम्नलिखित प्रश्नों का उत्तर दें

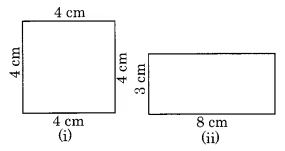
प्रश्न 10: निम्नलिखित में से किस आकृति का परिमाप अधिक है? उत्तर: (i) वर्ग का परिमाप = 4 × भुजा = 4 × 4 सेमी = 16 सेमी (ii) आयत का परिमाप = 2 [लंबाई चौड़ाई] = 2[8 सेमी 3 सेमी] = 2 × 11 सेमी = 22 सेमी। चूंकि 22 सेमी > 16 सेमी, इसलिए आयत का परिमाप वर्ग से अधिक है।

प्रश्न 11: एक एथलीट द्वारा 150 मीटर लंबाई और 80 मीटर चौड़ाई के आयताकार पार्क के 2 चक्कर लगाने पर कुल दूरी ज्ञात करें।

उत्तर: आयताकार पार्क की चौड़ाई b = 80 मीटर और लंबाई l = 150 मीटर है। पार्क का परिमाप = 2 (b + l) = 2 × (80 + 150) = 2 × 230 = 460 मीटर। दिया गया: एथलीट आयताकार पार्क के चारों ओर 2 चक्कर लगाता है। इसलिए, एथलीट द्वारा तय की गई कुल दूरी = 2 × 460 मीटर = 920 मीटर।

प्रश्न 12: एक दर्जी एक 20 सेमी के भुजा वाले वर्ग मेज़पोश के चारों ओर लेस डालना चाहता है। उसने बाजार से 1 मीटर लेस खरीदी। काम पूरा करने के बाद उसके पास बची लेस की लंबाई ज्ञात करें।

उत्तर: भुजा = 20 सेमी। वर्ग का परिमाप: S × 4 = 20 × 4 = 80 सेमी। लेस की लंबाई = 1 मीटर = 100 सेमी। बची हुई लेस: 100 - 80 = 20 सेमी।

Q13: एक आयताकार पार्क की लंबाई 50 मीटर है और उसका क्षेत्रफल 650 मीटर² है। इसके चौड़ाई का पता लगाएँ।

उत्तर: लंबाई = 50 मीटर

क्षेत्रफल = 650 मीटर²

तो, प्रश्न के अनुसार: आयत का क्षेत्रफल = लंबाई x चौड़ाई

650 = 50 x चौड़ाई

चौड़ाई = 650 / 50

चौड़ाई = 13 मीटर

Q14: एक कमरे के फर्श को कवर करने के लिए कितनी वर्ग टाइल्स की आवश्यकता होगी, जिसकी लंबाई 4 मीटर और चौड़ाई 3 मीटर है, यदि प्रत्येक वर्ग टाइल का पक्ष 0.2 मीटर है।

उत्तर: कमरे के फर्श को कवर करने के लिए आवश्यक वर्ग टाइल्स की संख्या जानने के लिए, हमें पहले कमरे का क्षेत्रफल वर्ग मीटर में निर्धारित करना होगा। आयत का क्षेत्रफल देने वाला सूत्र है:

क्षेत्रफल = लंबाई x चौड़ाई

इस मामले में, कमरे की लंबाई 4 मीटर और चौड़ाई 3 मीटर है, इसलिए कमरे का क्षेत्रफल है 4 x 3 = 12 वर्ग मीटर।

अगला, हमें एक एकल वर्ग टाइल का क्षेत्रफल निर्धारित करना होगा। एक वर्ग का क्षेत्रफल देने वाला सूत्र है:

क्षेत्रफल = पक्ष x पक्ष

इस मामले में, वर्ग टाइल का पक्ष 0.2 मीटर है, इसलिए एक टाइल का क्षेत्रफल है 0.2 x 0.2 = 0.04 वर्ग मीटर।

कमरे के फर्श को कवर करने के लिए आवश्यक टाइल्स की संख्या जानने के लिए, हम कमरे के क्षेत्रफल को एक टाइल के क्षेत्रफल से विभाजित कर सकते हैं:

12 वर्ग मीटर / 0.04 वर्ग मीटर = 300 टाइल्स

इसलिए, कमरे के फर्श को कवर करने के लिए आवश्यक वर्ग टाइल्स की संख्या 300 टाइल्स है।

Q15: एक समबाहु त्रिकोण के दो समान भुजाएँ 10 सेंटीमीटर हैं। यदि इसका परिमाप 32 सेंटीमीटर है, तो इसकी तीसरी भुजा की लंबाई ज्ञात करें।

त्रिकोण का परिमाप = सभी भुजाओं का योग

32 = 10 10 x

(तीसरी भुजा को x मानते हुए)

32 = 20 x

x = 32 - 20

x = 12 cm

Q16: एक तार की लंबाई 60 cm है। यदि इस तार का उपयोग निम्नलिखित आकृतियों को बनाने के लिए किया जाता है, तो प्रत्येक भुजा की लंबाई क्या होगी: (a) एक वर्ग (b) एक समभुज त्रिकोण (c) एक नियमित पंचकोण

Ans:

(a) तार की लंबाई = 60 cm
चूंकि, तार का उपयोग एक वर्ग बनाने के लिए किया गया है, इसलिए तार की लंबाई वर्ग का परिमाप हो जाती है।
परिमाप = 60 cm 4 × भुजा = 60 cm 60/4 = 15 भुजा = 15 cm
(b) दी गई
तार की लंबाई = 60 cm
यदि तार का उपयोग एक समभुज त्रिकोण बनाने के लिए किया जाता है, तो त्रिकोण का परिमाप = तार की लंबाई
मान लें कि त्रिकोण की भुजा a है
a + a + a = 60 ⇒ 3a = 60 ⇒ a = 20 cm
(c) दी गई, नियमित पंचकोण (सभी भुजाएँ समान)
परिमाप = 5 × भुजा = 60 cm
भुजा = 12 cm.

Q17: एक किसान का आयताकार बगीचा उसके घर के निकट है (जैसा चित्र में दिखाया गया है)। आयताकार बगीचा 200 m लंबा और 150 m चौड़ा है। इस बगीचे के तीन भुजाओं की बाड़ लगाने की लागत 12 प्रति मीटर के दर से क्या होगी?

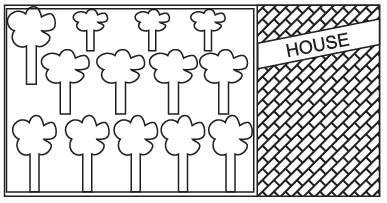
Ans:

बगीचे की लंबाई = 200 m
बगीचे की चौड़ाई = 150 m
बाड़ लगाने की लागत = 12 प्रति मीटर
हमें केवल 3 भुजाओं की बाड़ लगानी है = L + L + B = 200 + 200 + 150 = 550 m
बाड़ लगाने की लागत = 550 m × 12 = 6600 रुपये

Q18: निम्नलिखित आकृतियों में से प्रत्येक का परिमाप ज्ञात करें: (माप cm में दिए गए हैं)

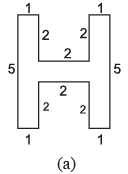
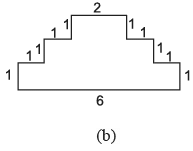
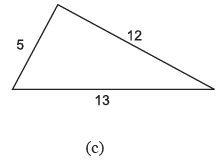
Ans:

(a) परिमाप = सभी भुजाओं का योग = 5 + 1 + 2 + 2 + 2 + 1 + 5 + 1 + 2 + 2 + 2 + 1 = 26 cm
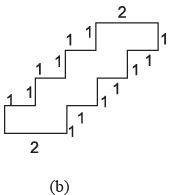
(b) परिमाप = सभी भुजाओं का योग = 1 + 1 + 1 + 1 + 1 + 2 + 1 + 1 + 1 + 1 + 1 + 6 = 18 cm
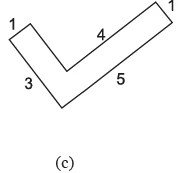
(c) परिमाप = सभी भुजाओं का योग = 13 + 5 + 12 = 30 cm

प्रश्न 19: निम्नलिखित आकृतियों का क्षेत्रफल ज्ञात करें: (माप सेंटीमीटर में दिए गए हैं)

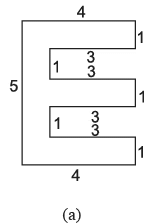
उत्तर: (क)

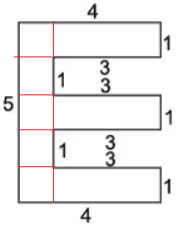
चित्र में 3 आयत और 5 वर्ग हैं।
एक आयत का क्षेत्रफल = लम्बाई (l) × चौड़ाई (b) = 4 × 1
वर्ग की भुजा = 1
आयत की भुजाएँ = लम्बाई = 1 और चौड़ाई = 3
3 × 1 = 3, आयत की संख्या 3 है।
3 × एक आयत का क्षेत्रफल = 3 × 3 = 9
वर्ग का क्षेत्रफल = भुजा² = 1 × 1 = 1
वर्गों की संख्या 5 = 5 × 1 = 5
कुल क्षेत्रफल = 9 + 5 = 14 वर्ग सेंटीमीटर

(ख)

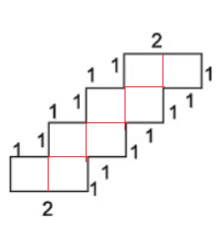
वर्गों की संख्या = 8
एक वर्ग का क्षेत्रफल = 1 × 1 = 1
सभी वर्गों का क्षेत्रफल = 8 × 1 = 8 वर्ग सेंटीमीटर

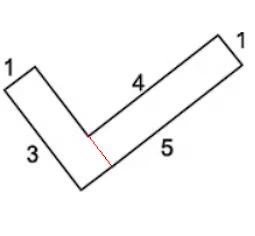
आयत 1 का क्षेत्रफल = लम्बाई × चौड़ाई = 3 × 1 = 3
आयत का क्षेत्रफल = लम्बाई × चौड़ाई = 4 × 1 = 4
कुल क्षेत्रफल = 3 + 4 = 7 वर्ग सेंटीमीटर

प्रश्न 20: एक घर के परिसर की बाड़ लगाने की लागत ₹5452 है। यदि दर ₹94 प्रति मीटर है, तो परिसर का परिधि ज्ञात करें। यदि चौड़ाई 10 मीटर है, तो इसकी लम्बाई ज्ञात करें।

बाड़ लगाने की लागत = ₹5452
बाड़ लगाने की दर = ₹94 प्रति मीटर
∴ परिसर का परिधि = 5452 ÷ 94 = 58 मीटर
अब परिसर की चौड़ाई = 10 मीटर।
2 × (लम्बाई + चौड़ाई) = 58 मीटर
∴ लम्बाई + चौड़ाई = 58 ÷ 2 मीटर = 29 मीटर
∴ परिसर की लम्बाई = 29 मीटर – 10 मीटर = 19 मीटर।

The document Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: Worksheet Solutions: परिधि और क्षेत्रफल - 2 for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for Worksheet Solutions: परिधि और क्षेत्रफल - 2 have been prepared according to the Class 6 exam syllabus. Information about Worksheet Solutions: परिधि और क्षेत्रफल - 2 covers topics like and Worksheet Solutions: परिधि और क्षेत्रफल - 2 Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Worksheet Solutions: परिधि और क्षेत्रफल - 2.

Introduction of Worksheet Solutions: परिधि और क्षेत्रफल - 2 in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & Worksheet Solutions: परिधि और क्षेत्रफल - 2 in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about Worksheet Solutions: परिधि और क्षेत्रफल - 2

In this doc you can find the meaning of Worksheet Solutions: परिधि और क्षेत्रफल - 2 defined & explained in the simplest way possible. Besides explaining types of Worksheet Solutions: परिधि और क्षेत्रफल - 2 theory, EduRev gives you an ample number of questions to practice Worksheet Solutions: परिधि और क्षेत्रफल - 2 tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

practice quizzes

MCQs

Semester Notes

Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

study material

shortcuts and tricks

Worksheet Solutions: परिधि और क्षेत्रफल - 2 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Objective type Questions

Previous Year Questions with Solutions

Important questions

Free

mock tests for examination

ppt

Summary

past year papers

Sample Paper

pdf

Viva Questions

Exam

video lectures

Extra Questions

;

Additional Information about Worksheet Solutions: परिधि और क्षेत्रफल - 2 for Class 6 Preparation

Worksheet Solutions: परिधि और क्षेत्रफल - 2 Free PDF Download

The Worksheet Solutions: परिधि और क्षेत्रफल - 2 is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Worksheet Solutions: परिधि और क्षेत्रफल - 2 now and kickstart your journey towards success in the Class 6 exam.

Importance of Worksheet Solutions: परिधि और क्षेत्रफल - 2

The importance of Worksheet Solutions: परिधि और क्षेत्रफल - 2 cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Worksheet Solutions: परिधि और क्षेत्रफल - 2 Notes

Worksheet Solutions: परिधि और क्षेत्रफल - 2 Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Worksheet Solutions: परिधि और क्षेत्रफल - 2. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Worksheet Solutions: परिधि और क्षेत्रफल - 2 Notes on EduRev are your ultimate resource for success.

Worksheet Solutions: परिधि और क्षेत्रफल - 2 Class 6 Questions

The "Worksheet Solutions: परिधि और क्षेत्रफल - 2 Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Worksheet Solutions: परिधि और क्षेत्रफल - 2 on the App

Students of Class 6 can study Worksheet Solutions: परिधि और क्षेत्रफल - 2 alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Worksheet Solutions: परिधि और क्षेत्रफल - 2, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Worksheet Solutions: परिधि और क्षेत्रफल - 2 is prepared as per the latest Class 6 syllabus.

Education Revolution