भिन्न (Fractions) Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

परिचय

एक भिन्न एक संपूर्ण का हिस्सा दर्शाने का एक तरीका है।

मान लीजिए, एक पिज़्ज़ा को दो समान टुकड़ों में काटा गया है। यदि आप पिज़्ज़ा को दो समान टुकड़ों में विभाजित करते हैं, तो हर बच्चे का हिस्सा 1/2 होगा।

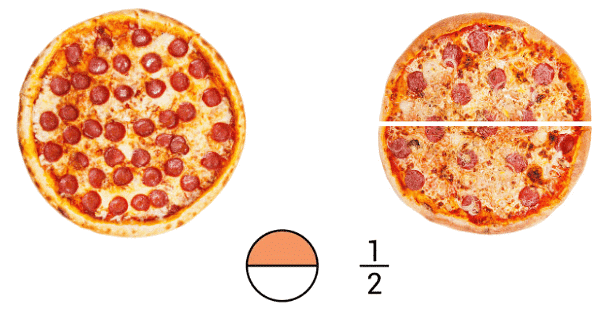
अब, यदि आप पिज़्ज़ा को चार समान टुकड़ों में काटते हैं, तो हर बच्चे का हिस्सा 1/4 होगा।

भिन्नें हमें उन परिस्थितियों को समझाने और स्पष्ट करने में मदद करती हैं जहां कुछ समान भागों में विभाजित होता है।

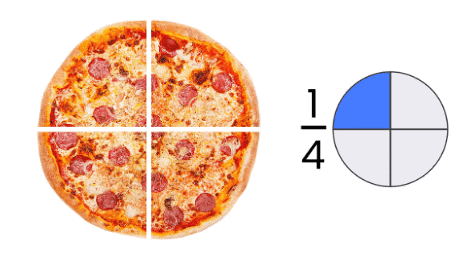
आइए इस अवधारणा को बेहतर समझते हैं।

एक भिन्न

भिन्न का अर्थ एक समूह या क्षेत्र का हिस्सा है।

जब हम एक भिन्न को देखते हैं, तो इसमें दो महत्वपूर्ण संख्याएँ होती हैं:

• संख्यात्मक (ऊपरी संख्या): यह हमें बताती है कि हमारे पास संपूर्ण का कितने हिस्से हैं या हम कितने हिस्से उपयोग कर रहे हैं। उदाहरण के लिए, भिन्न 5/12 में, संख्यात्मक 5 है, जिसका अर्थ है कि हमारे पास कुल 12 में से 5 हिस्से हैं।

• हर (निचली संख्या): यह बताती है कि संपूर्ण को कितने समान भागों में विभाजित किया गया है। 12 में, हर 12 है, जिसका अर्थ है कि संपूर्ण को 12 समान भागों में विभाजित किया गया है।

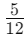
आइए एक उदाहरण के माध्यम से भिन्नों को समझते हैं: एथन अपने घर पर अपना जन्मदिन मना रहा है। उसकी माँ ने उसके जन्मदिन के लिए एक केक बनाया है। जब उसके दोस्त घर आए, तो उसने केक को काट दिया। उसकी माँ चाहती है कि केक को सभी दोस्तों के बीच समान रूप से वितरित किया जाए। पार्टी में कुल छह लोग (एथन की माँ सहित) हैं। इसलिए, उसकी माँ केक को 6 समान हिस्सों में काटती है।

केक के भिन्न

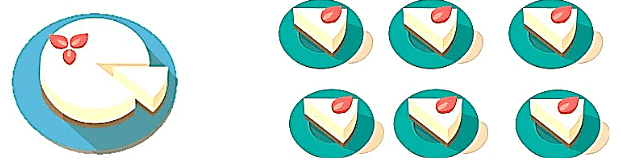
क्या आप बता सकते हैं कि एथन को केक का कितना हिस्सा मिलता है?

केक के कुल टुकड़े = 6 एथन को (एक-छठा) हिस्सा मिलता है। इसलिए, एथन ने केक के छह हिस्सों में से एक हिस्सा खाया।

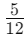
यहाँ 1 संख्याकर है और 6 हर में है।

भिन्नात्मक इकाइयाँ और समान भाग

भिन्नात्मक इकाई उस पूरे का एक भाग है जिसे समान खंडों में विभाजित किया गया है। जब हम किसी चीज़ को समान भागों में बाँटते हैं, तो प्रत्येक भाग को भिन्नात्मक इकाई कहा जाता है।

उदाहरण के साथ समझना

कल्पना करें कि आपके पास एक चॉकलेट बार है जिसे आप अपने दोस्तों के साथ बाँटना चाहते हैं। मान लीजिए कि आपके पास 1 चॉकलेट बार है और 4 दोस्त हैं, जिनमें आप भी शामिल हैं, इसका अर्थ है कि आपको चॉकलेट को 4 समान टुकड़ों में बाँटना होगा।

• आपको जो भी टुकड़ा मिलता है, वह पूरे चॉकलेट बार की एक भिन्नात्मक इकाई है। इस मामले में, चॉकलेट को 4 समान भागों में बाँटा गया है, प्रत्येक टुकड़ा चॉकलेट बार का 1/4 है।
• अब, एक अलग परिदृश्य पर विचार करें। आपके पास अभी भी 1 चॉकलेट बार है, लेकिन इस बार आपको इसे 9 दोस्तों के साथ बाँटना है। यदि आप चॉकलेट बार को 9 समान भागों में बाँटते हैं, तो प्रत्येक टुकड़ा चॉकलेट बार का 1/9 होगा।

तुलना: कौन सा टुकड़ा बड़ा है, 1/4 या 1/9? जब आप चॉकलेट को 4 भागों में बाँटते हैं, तो प्रत्येक टुकड़ा बड़ा होता है क्योंकि इसे साझा करने वाले लोग कम होते हैं। इसलिए, 1/4, 1/9 से बड़ा है।

यह उदाहरण यह दर्शाता है कि जैसे-जैसे भागों की संख्या बढ़ती है, प्रत्येक भिन्नात्मक इकाई (या टुकड़ा) छोटी होती जाती है।

अतीत से ज्ञान: भारत में भिन्नों का इतिहास

• भारत में भिन्नों का एक समृद्ध इतिहास है, जो प्राचीन समय से शुरू होता है जब उन्हें विभिन्न ग्रंथों में पहचाना और नामित किया गया था।
• ऋग्वेद में, जो भारतीय साहित्य के सबसे पुराने ग्रंथों में से एक है, भिन्नों को "त्रिपदा" कहा गया था।
• यह संकेत करता है कि आधुनिक भारतीय भाषाओं में उपयोग किए जाने वाले भिन्नों के लिए शब्द प्राचीन इतिहास में निहित हैं।
• कुल मिलाकर, भारत में भिन्नों की वर्तमान समझ और नामकरण का एक गहरा ऐतिहासिक पृष्ठभूमि है।

भिन्नात्मक इकाइयाँ एक पूरे के भाग के रूप में

अंशात्मक इकाईअंशात्मक इकाई कहा जाता है।

कल्पना करें कि एक पारंपरिक मिठाई है जिसे "चikki" कहा जाता है, जो गुड़ और मेवों से बनी एक आयताकार पट्टी है। मान लीजिए कि आपके पास एक पूरा चikki है और आप इसे समान भागों में विभाजित करना चाहते हैं।

चikki को 2 भागों में विभाजित करना:

• यदि आप चikki को 2 समान टुकड़ों में तोड़ते हैं, तो प्रत्येक टुकड़ा पूरे चikki का 1/2 है। यहाँ, अंशात्मक इकाई 1/2 है, जिसका अर्थ है कि प्रत्येक टुकड़ा मूल चikki का आधा है।

चikki को 6 भागों में विभाजित करना:

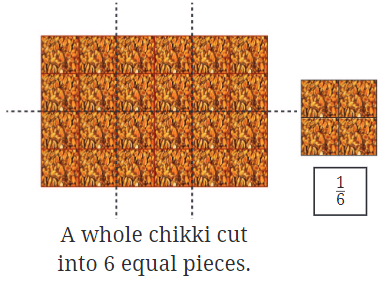
• यदि आप उसी चikki को 6 समान टुकड़ों में तोड़ते हैं, तो प्रत्येक टुकड़ा पूरे चikki का 1/6 है। यहाँ, अंशात्मक इकाई 1/6 है, जिसका अर्थ है कि प्रत्येक टुकड़ा मूल चikki का एक-छठा है।

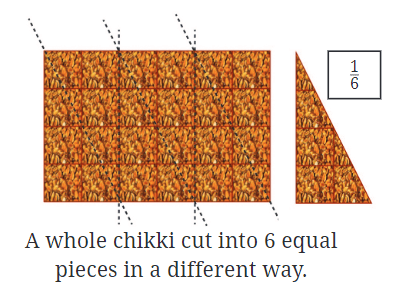
विभिन्न आकारों को समझना: कभी-कभी, भले ही टुकड़े दिखने में भिन्न हों, वे फिर भी एक समान आकार के हो सकते हैं। उदाहरण के लिए, यदि आप चikki को 6 समान टुकड़ों में काटते हैं, तो प्रत्येक टुकड़ा कट के आधार पर भिन्न दिखाई दे सकता है, लेकिन प्रत्येक एक समान रूप से 1/6 पूरे चikki का ही रहेगा।

सही और गलत अंश:

जिन अंशों पर हमने पहले चर्चा की, जैसे 1/2 और 1/6, उन्हें सही अंश कहा जाता है। इसके विपरीत, गलत अंश तब होते हैं जब अंश (numerator) हर (denominator) से बड़ा या उसके बराबर होता है, जैसे 5/4 या 3/2।

पूर्ण संख्याओं के साथ अंशों का गुणन:

किसी पूर्ण संख्या को सही या गलत अंश से गुणा करने के लिए, पूर्ण संख्या को अंश के अंश (numerator) से गुणा करें और फिर हर (denominator) से विभाजित करें। उदाहरण के लिए, यदि फरिदा के पास 20 गिल्ली हैं और रेशमा के पास उस संख्या का 1/5 है, तो हम यह पता कर सकते हैं कि रेशमा के पास कितनी गिल्ली हैं:

रेशमा के पास 1/5 × 20 = 4 कागज़ी गेंदें हैं।

भिन्नात्मक इकाइयों का उपयोग करके मापना

भिन्नात्मक इकाइयों का उपयोग करके मापने का अर्थ है किसी पूरे वस्तु या मात्रा को छोटे, समान भागों में विभाजित करना ताकि मापना आसान हो सके। जब कुछ इतना बड़ा हो कि उसे पूरी तरह से नहीं मापा जा सके, तो हम इसे भिन्नों में बाँट सकते हैं, जो छोटे, समान खंड होते हैं। यह दृष्टिकोण हमें यह वर्णन करने और समझने में मदद करता है कि हमारे पास कुछ कितना है, भले ही वह एक पूर्ण वस्तु न हो।

उदाहरण के साथ समझना

कल्पना करें कि आपके पास एक एकलाई कागज़ की पट्टी है जो एक इकाई लंबी है। यदि आप इस पट्टी को दो समान भागों में मोड़ते हैं, तो प्रत्येक भाग अब मूल पट्टी का 1/2 (आधा) है। यदि आप इसे फिर से चार समान भागों में मोड़ते हैं, तो प्रत्येक भाग मूल पट्टी का 1/4 (चौथाई) बन जाता है।

अब, एक पूरी रोटी (गोल चपाती) पर विचार करें। यदि आप रोटी को दो समान भागों में काटते हैं, तो प्रत्येक भाग पूरे रोटी का 1/2 होता है। यदि आप इसे चार समान भागों में काटते हैं, तो प्रत्येक भाग पूरे रोटी का 1/4 होता है।

इस तरह से 1/2, 1/4 जैसी भिन्नात्मक इकाइयों का उपयोग करके हम किसी पूरे का माप और वर्णन कर सकते हैं।

भिन्नों को पढ़ना

• भिन्नों को विभिन्न तरीकों से पढ़ा जा सकता है। उदाहरण के लिए, भिन्न 3/4 को "तीन चौथाई" या "तीन पर चार" के रूप में पढ़ा जा सकता है। हालांकि, इसे "तीन गुना एक-चौथाई" के रूप में पढ़ना भिन्न के आकार को समझने में आसान बनाता है। इस तरह, हम देखते हैं कि भिन्नात्मक इकाई क्या है (1/4) और इनमें से कितनी इकाइयाँ हैं (3)।
• एक भिन्न में, ऊपर का संख्या संख्यक होता है, और नीचे का संख्या हर होता है। उदाहरण के लिए, भिन्न 5/6 में, 5 संख्यक है, और 6 हर है।

भिन्नों के व्यावहारिक अनुप्रयोग

भिन्नों का उपयोग कई दैनिक परिस्थितियों में किया जाता है। उदाहरण के लिए:

• जब खाना बनाते हैं, तो व्यंजनों में सामग्री की मात्रा भिन्नात्मक हो सकती है, जैसे 1/2 कप चीनी या 3/4 चम्मच नमक।
• भिन्नाएँ दूरी को मापने में भी महत्वपूर्ण होती हैं, जैसे जब एक बढ़ई एक लकड़ी के टुकड़े को उसकी लंबाई के 1/3 में काटने के लिए मापता है।

भिन्नों को समझने से हमें दैनिक कार्यों में सटीक माप और गणनाएँ करने की अनुमति मिलती है।

संख्यात्मक रेखा पर भिन्न लंबाई को चिह्नित करना

संख्यात्मक रेखा पर भिन्नों का प्रतिनिधित्व करना इसका मतलब है कि हम भिन्नों को संख्यात्मक रेखा पर अंकित कर सकते हैं, जो कि पूर्णांक और संख्याओं को अंकित करने के समान है। भिन्नें किसी पूर्ण का भाग प्रदर्शित करती हैं।

इसलिए, संख्यात्मक रेखा पर भिन्नें को उस पूर्ण को समान भागों में बांटकर प्रदर्शित किया जाता है, अर्थात 0 से 1 तक, और उन समान भागों की संख्या भिन्न के हर के नीचे लिखे गए संख्या के समान होगी। उदाहरण के लिए, 1/8 को संख्यात्मक रेखा पर प्रदर्शित करने के लिए, हमें 0 से 1 तक 8 समान भागों में विभाजित करना होगा और पहले भाग को 1/8 के रूप में चिह्नित करना होगा।

1. संख्यात्मक रेखा के बुनियादी सिद्धांत समझें:

• संख्यात्मक रेखा एक सीधी रेखा है जहां संख्याएँ समान दूरी पर रखी जाती हैं। पूर्णांक जैसे 0, 1, 2 आदि इस रेखा पर अंकित होते हैं।

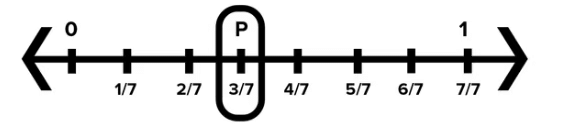
2. प्रदर्शित करने के लिए भिन्न की पहचान करें:

• उदाहरण के लिए, आप भिन्न 3/7 को प्रदर्शित करना चाहते हैं। यह भिन्न दर्शाती है कि आपके पास 7 समान भागों में से 3 भाग हैं।

3. 0 और 1 के बीच की लंबाई को विभाजित करें:

• चूंकि हर 7 है, 0 और 1 के बीच की लंबाई को 7 समान भागों में विभाजित करें।

4. भिन्न को चिह्नित करें:

• 0 से 3 भागों की गिनती करें। जिस बिंदु पर आप रुकते हैं, वह संख्यात्मक रेखा पर 3/7 है। इस बिंदु को 3/7 के रूप में चिह्नित करने के लिए "P" के रूप में चिह्नित करें।

5. अन्य संबंधित भिन्नों को चिह्नित करें:

• 0/7: यह बस 0 है, इसलिए इसे रेखा के प्रारंभिक बिंदु पर चिह्नित करें।
• 7/7: चूंकि 7/7 1 के बराबर है, इसे संख्यात्मक रेखा पर 1 के बिंदु पर चिह्नित करें।

उदाहरण:

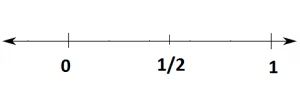
• एक भिन्न पर विचार करें 1/2। 1/2 शून्य से बड़ा है, लेकिन 1 से छोटा है। शून्य और 1 के बीच के क्षेत्र को दो समान भागों में विभाजित करें। हम एक भाग को भिन्न 1/2 के रूप में दिखा सकते हैं।

• एक और भिन्न पर विचार करें 1/5। 1/5 शून्य से बड़ा है, लेकिन 1 से छोटा है। शून्य और 1 के बीच के क्षेत्र को पांच समान भागों में विभाजित करें। हम पहले भाग को 1/5, दूसरे को 2/5, तीसरे को 3/5, चौथे को 4/5, और पांचवे भाग को 5/5=1 के रूप में दिखा सकते हैं।

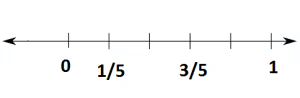
अवैध भिन्नों को समझना

• एक भिन्न जिसमें संख्याप्रमुख (ऊपरी संख्या) संख्यापाद (निचली संख्या) से बड़ा होता है। इसका मतलब है कि भिन्न 1 या उससे अधिक मात्रा का प्रतिनिधित्व करती है। उदाहरण के लिए, 9/5 एक अवैध भिन्न है क्योंकि इसका मतलब है कि 9 भागों को 5 के समूहों में विभाजित किया जा रहा है। इसका अर्थ है कि आपके पास 9 भाग हैं, और प्रत्येक भाग एक पूरे का एक-पांचवां हिस्सा है। चूंकि 9, 5 से अधिक है, यह भिन्न 1 से बड़ी है।
• 9/5 को समझने के लिए, आप इसे 9 को 5 से विभाजित करने के रूप में सोच सकते हैं। जब आप यह विभाजन करते हैं, तो परिणाम 1 पूरा (5/5) होता है, जिसमें 4 भाग शेष रहते हैं। इसलिए, 9/5 को इस प्रकार लिखा जा सकता है: 1 (पूरा) 4/5 (शेष भाग)।

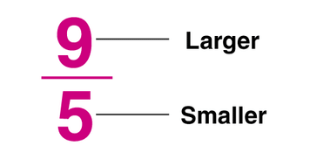
मिश्रित भिन्नें

एक मिश्रित भिन्न एक पूर्णांक को एक उचित भिन्न के साथ मिलाकर बनता है। यह दिखाता है कि कितने पूरे भाग हैं, साथ ही एक अन्य भाग का भिन्न भी।

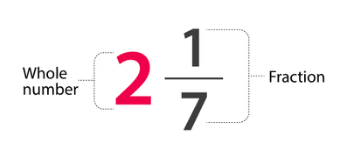
• उदाहरण के लिए, यदि आपके पास 1 पूरा पिज्जा और एक अतिरिक्त आधा पिज्जा है, तो इसे एक मिश्रित भिन्न के रूप में लिखा जा सकता है: 1 1/2। इसका मतलब है कि आपके पास 1 पूरा पिज्जा है और एक और 1/2 पिज्जा है।

एक से अधिक भिन्नों को मिश्रित संख्याओं के रूप में लिखना

मिश्रित संख्याओं को समझना

जब हम किसी भिन्न का सामना करते हैं जो एक से अधिक है, तो हम इसे एक मिश्रित संख्या के रूप में व्यक्त कर सकते हैं। एक मिश्रित संख्या एक पूर्णांक को एक भिन्न के साथ मिलाकर बनती है, जो यह दर्शाती है कि हमारे पास कितने पूरे भाग हैं और कितना भाग शेष है।

असामान्य भिन्नों की व्याख्या

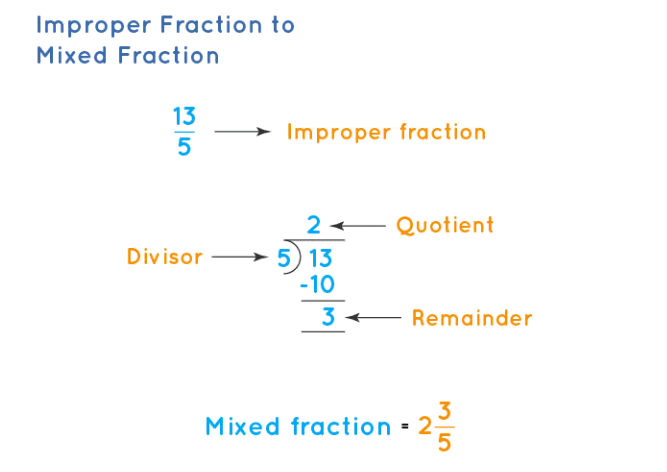
1. असामान्य भिन्न को मिश्रित भिन्न में परिवर्तित करना: एक असामान्य भिन्न को मिश्रित भिन्न के रूप में व्यक्त किया जा सकता है, जिसमें असामान्य भिन्न के अंश को हर (डिनॉमिनेटर) से विभाजित करके भागफल और बाकी प्राप्त किया जाता है।

अंश को हर से विभाजित करें:

• अंश वह संख्या है जो ऊपर होती है, और हर वह संख्या है जो भिन्न के नीचे होती है। विभाजन करें ताकि आपको एक भागफल (पूर्णांक भाग) और शेष (बाकी भाग) मिले।

मिश्रित भिन्न का निर्माण करें:

• भागफल मिश्रित भिन्न का पूर्णांक भाग बनता है।
• शेष भिन्न का नया अंश बनता है, और हर वही रहता है।
• मिश्रित भिन्न को इस प्रकार लिखा जाएगा:

तब मिश्रित भिन्न होगा।

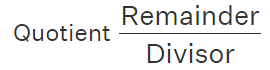
उदाहरण:

2. मिश्रित भिन्न को असामान्य भिन्न में परिवर्तित करना:

पूर्णांक को हर (डिनोमिनेटर) से गुणा करें:

• मिश्रित भिन्न के पूर्णांक भाग को लें और इसे हर (भिन्न का निचला संख्या) से गुणा करें।

संख्यात्मक गुणांक को उत्पाद में जोड़ें:

• गुणा करने के बाद, संख्यात्मक गुणांक (भिन्न का ऊपरी संख्या) को पहले चरण के उत्पाद में जोड़ें।

असामान्य भिन्न बनाएँ:

• चरण 2 से प्राप्त योग असामान्य भिन्न का संख्यात्मक हिस्सा बनता है। हर वही रहता है जैसा कि मूल भिन्न में था।

आइए निम्नलिखित चरणों और दी गई व्याख्या का उपयोग करके इस मिश्रित भिन्न को असामान्य भिन्न में परिवर्तित करें।

• चरण 1: मिश्रित भिन्न के हर को पूर्णांक भाग से गुणा करें। इस मामले में, 5 × 2 = 10
• चरण 2: चरण 1 से प्राप्त उत्पाद में संख्यात्मक गुणांक जोड़ें। यहाँ, 4 + 10 = 14।
• चरण 3: चरण 2 से प्राप्त योग को संख्यात्मक/हर रूप में लिखें। यहाँ, यह 14/5 होगा।

समान भिन्न

ये ऐसे भिन्न हैं जो समान मूल्य या पूरे का हिस्सा प्रस्तुत करते हैं, भले ही उनके संख्यात्मक और हर अलग हों।

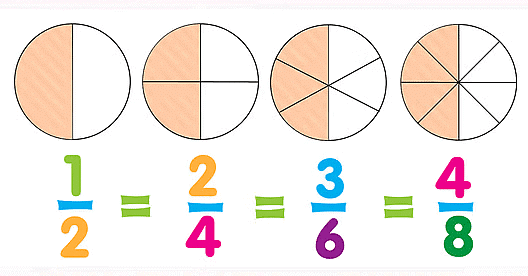
समान भिन्न लंबाई खोजने के लिए भिन्न दीवार का उपयोग!

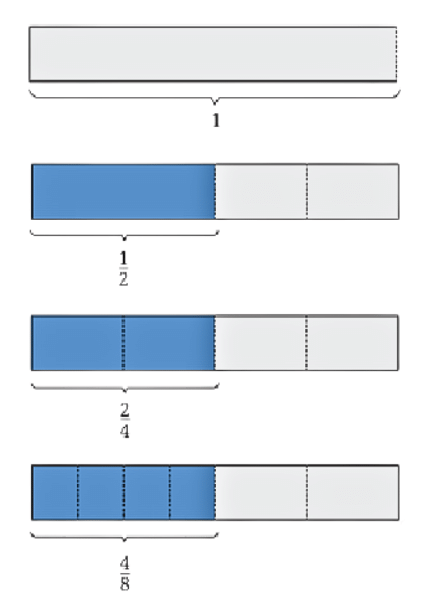
समान भिन्न विभिन्न भिन्न होते हैं जो समान मात्रा का प्रतिनिधित्व करते हैं। यह देखने के लिए कि क्या भिन्न जैसे 1/2 और 2/4 समान हैं, हम कागज की पट्टियों का उपयोग कर सकते हैं।

1/2, 2/4 और 4/8 समान भिन्न हैं, जैसा कि कागज की पट्टियों का उपयोग करके दिखाया गया है। आप विभिन्न भिन्नों की तुलना और दृश्यता को और अधिक प्रभावी ढंग से देखने के लिए एक भिन्न दीवार बना सकते हैं।

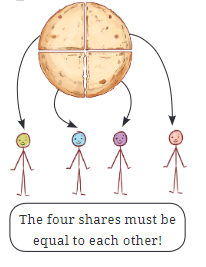
समान अंशों को समझना: समान हिस्सों के माध्यम से

जब एक रोटी को चार बच्चों के बीच समान रूप से बांटा जाता है, तो प्रत्येक बच्चे को पूरी रोटी का एक हिस्सा मिलता है। चित्र में दिखाया गया है कि रोटी को चार समान भागों में कैसे काटा गया है।

प्रत्येक बच्चे का रोटी का हिस्सा 1/4 है। यह समान अंशों को प्रदर्शित करता है, क्योंकि हिस्सों को अन्य रूपों में भी दिखाया जा सकता है। उदाहरण के लिए, किसी अंश का व्युत्क्रम प्राप्त करने के लिए, ऊपर और नीचे के नंबरों को स्वैप किया जाता है। इसलिए, 1/4 का व्युत्क्रम 4/1 है।

हम अंशों का उपयोग एक आयत के क्षेत्रफल को बताने के लिए भी कर सकते हैं। उदाहरण के लिए, यदि लंबाई 3/4 है और चौड़ाई 1/2 है, तो क्षेत्रफल इस प्रकार निकाला जा सकता है:

• क्षेत्रफल: लंबाई x चौड़ाई = 3/4 x 1/2 = 3/8 वर्ग इकाइयाँ।

कैसे समान अंश खोजें

उपर और नीचे दोनों को गुणा करना: समान अंश खोजने के लिए, ऊपर (संख्याप्रमुख) और नीचे (हर) दोनों को एक ही संख्या से गुणा करें।

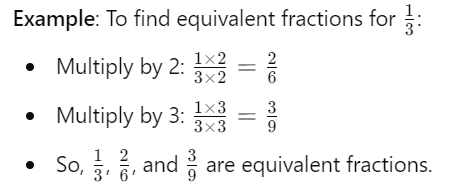
उपर और नीचे दोनों को विभाजित करना: वैकल्पिक रूप से, आप समान अंश खोजने के लिए ऊपर और नीचे दोनों को एक ही संख्या से विभाजित कर सकते हैं।

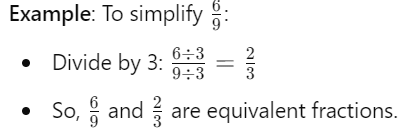
समान अंश एक ही पूरे का एक ही भाग दर्शाते हैं क्योंकि वे एक ही अनुपात को व्यक्त करने के विभिन्न तरीके हैं। जब आप संख्याप्रमुख और हर को एक ही संख्या से गुणा या विभाजित करते हैं, तो आप वास्तव में अंश को स्केल कर रहे होते हैं लेकिन कुल मिलाकर वही मूल्य बनाए रखते हैं।

एक अंश को सबसे छोटे रूप में व्यक्त करना (या इसके सरलतम रूप में)

सबसे छोटे रूप को समझना

एक अंश सबसे छोटे रूप में होता है जब ऊपर का नंबर (संख्याप्रमुख) और नीचे का नंबर (हर) 1 के अलावा कोई सामान्य गुणांक साझा नहीं करते हैं। इसका मतलब है कि दोनों नंबर जितने छोटे हो सकते हैं उतने छोटे हैं और अंश को और नहीं घटाया जा सकता।

• भिन्नों को उनके सबसे छोटे रूप में लाने के लिए, अंश और हर (डिनॉमिनेटर) को उनके महत्तम सम गुणांक (GCF) से विभाजित करें।

महत्वपूर्ण नोट: महत्तम सम भाजक (GCD) भिन्नों को सरल करने में महत्वपूर्ण है, क्योंकि यह सबसे बड़े संख्या को खोजने में मदद करता है जो अंश और हर को समान रूप से विभाजित कर सकता है।

चरण-दर-चरण उदाहरण: 36/60 को सरल बनाना

• चरण 1: दोनों 36 और 60 सम हैं, इसलिए 2 से विभाजित करें:

• चरण 2: अब, 18 और 30 भी सम हैं, इसलिए फिर से 2 से विभाजित करें:

• चरण 3: अगला, 9 और 15 3 के गुणांक हैं, इसलिए दोनों को 3 से विभाजित करें:

• अब, 3/5 अपने सबसे सरल रूप में है क्योंकि 3 और 5 के अलावा कोई भी सामान्य भाजक नहीं है।

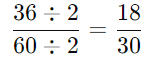
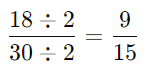
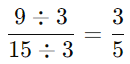
उदाहरण: भिन्न 11/33 का सबसे सरल रूप खोजें

भिन्नों की तुलना

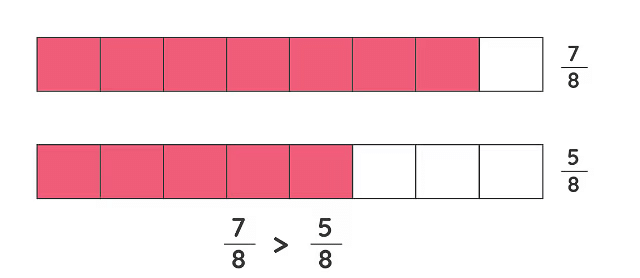
1. समान भिन्नों की तुलना

भिन्नों की तुलना में यह पता लगाना शामिल है कि दो या अधिक भिन्नों में से कौन सी बड़ी या छोटी है। इसे एक सरल तरीके से किया जा सकता है, जिसमें उन्हें समान हर वाले समांतर भिन्नों में परिवर्तित किया जाता है। जब भिन्नों का हर समान होता है, तो हम सीधे अंश (ऊपरी संख्या) की तुलना कर सकते हैं ताकि यह स्थापित किया जा सके कि कौन सी भिन्न बड़ी है।

भिन्नों के साथ काम करते समय प्रतिवर्ती के बारे में जानना भी उपयोगी है। एक भिन्न का प्रतिवर्ती उसके अंश और हर को पलटकर पाया जाता है।

यहाँ भिन्नों 4/9 और 5/7 की तुलना करने का तरीका है:

• चरण 1: एक सामान्य हर पहचानें। यह एक संख्या है जो दोनों हर (9 और 7) में विभाजित हो सकती है। यहाँ, सामान्य हर 63 है।
• चरण 2: प्रत्येक भिन्न को सामान्य हर के अनुसार समायोजित करें: 4/9 को 28/63 में बदलें क्योंकि 4 × 7 = 28 और 9 × 7 = 63। 5/7 को 45/63 में बदलें क्योंकि 5 × 9 = 45 और 7 × 9 = 63।
• चरण 3: अब, अंशों (28 और 45) की तुलना करें: चूंकि 45 > 28 है, यह दिखाता है कि 5/7, 4/9 से बड़ी है।

2. असमान भिन्नों की तुलना

• यदि दो भिन्नों का अंश समान हो लेकिन हर के हर में भिन्न भिन्न भाजक हों, तो छोटी भाजक वाली भिन्न बड़ी होती है।
• असमान भाजकों वाली भिन्नों की तुलना करने के लिए, हमें उन्हें समान भाजकों में बदलना होगा, जिसके लिए हमें भाजकों का Least Common Multiple (LCM) खोजना होगा। जब भाजक समान हो जाएंगे, तो हम भिन्नों की तुलना आसानी से कर सकते हैं।

उदाहरण: तुलना करें: 1/4 और 2/3।

चरण 1: सबसे पहले, दिए गए भिन्नों के भाजकों पर ध्यान दें, अर्थात् 1/4 और 2/3। चूंकि भाजक भिन्न हैं, उन्हें समान करने के लिए 4 और 3 का LCM खोजें। LCM(4,3) = 12।

चरण 2: अब, दिए गए भिन्नों को इस तरह से बदलें कि उनके भाजक समान हो जाएं। इसलिए, पहले भिन्न को 3/3 से गुणा करें, अर्थात् 1/4 × 3/3 = 3/12।

चरण 3: इसी तरह, दूसरे भिन्न को 4/4 से गुणा करें, अर्थात् 2/3 × 4/4 = 8/12। इस प्रकार, पहला भिन्न 3/12 हो जाता है और दूसरा 8/12।

चरण 4: प्राप्त नई भिन्नों की तुलना करें, अर्थात् 3/12 और 8/12। चूंकि भाजक समान हैं, हम अंशों की तुलना करेंगे। हम देख सकते हैं कि 3 < />

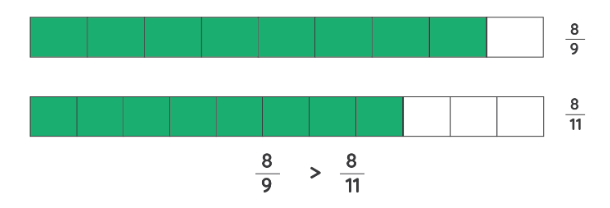
चरण 5: बड़ी संख्यावाला भिन्न बड़ा भिन्न होता है। इसलिए, 8/12 > 3/12। इस प्रकार, 2/3 > 1/4।

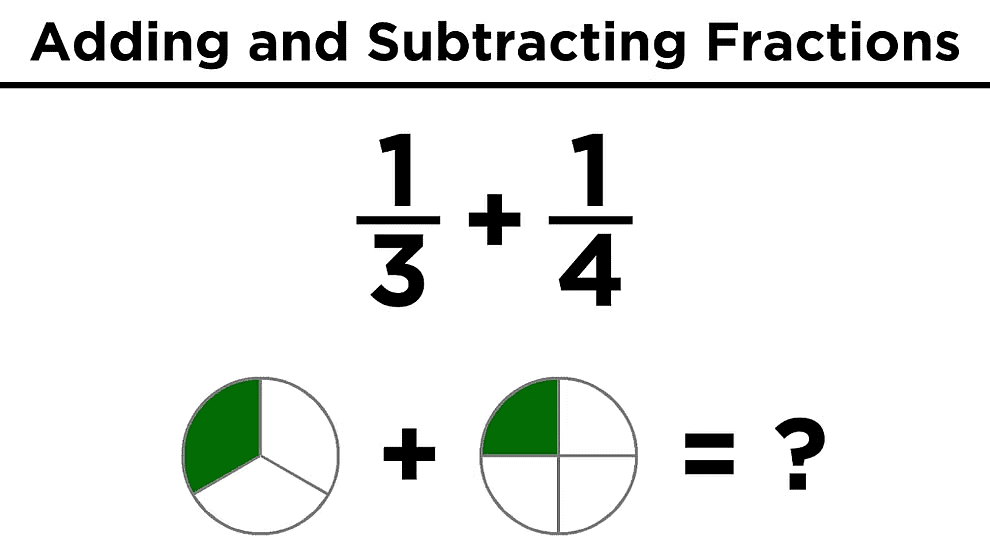
भिन्नों का जोड़ और घटाव

भिन्नों का जोड़ और घटाव का अर्थ है संपूर्ण के हिस्सों को एक साथ लाना या घटाना। भिन्नों को जोड़ने या घटाने के लिए, उनके नीचे का संख्या (हर) समान होना चाहिए। यदि वे समान नहीं हैं, तो आपको पहले एक सामान्य हर खोजना होगा। यह आमतौर पर हर के सबसे छोटे गुणांक (LCM) होता है।

1. समान हर वाले भिन्नों का जोड़ और घटाव:

जब हम समान भिन्नों को जोड़ते या घटाते हैं, तो हम उनके अंशों को जोड़ते या घटाते हैं और हर समान रहता है।

1)

दो भिन्न समान भिन्न हैं, इसलिए हम उनके अंशों को जोड़ते हैं और हर को समान रखते हैं। = =

2) −

यहां, दिए गए भिन्न समान भिन्न हैं। इसलिए, हम उनके अंशों को घटाते हैं और हर को समान रखते हैं। − = =

2. विभिन्न हर वाले दो भिन्नों का जोड़ और घटाव:

जब हम असमान भिन्नों को जोड़ते या घटाते हैं, तो हम निम्नलिखित चरणों का पालन करते हैं:

1)

दिए गए भिन्न असमान भिन्न हैं, इसलिए हम पहले उनके हर का LCM खोजते हैं।

8 और 24 का LCM = 2 × 2 × 2 × 3 = 24 अब, हम भिन्नों को समान भिन्नों में बदलते हैं। (भिन्नों के हर को 24 में बदलना)

= और

= =

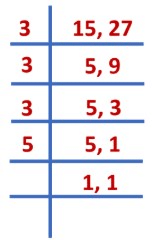
2) -

चूंकि दिए गए भिन्न असमान भिन्न हैं, हम उनके हर का LCM खोजते हैं।

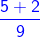
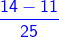
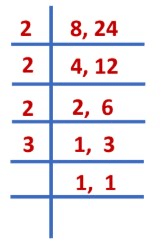
15 और 27 का LCM = 3 × 3 × 3 × 5 = 135। इसके बाद, हम भिन्नों को समान भिन्नों में परिवर्तित करेंगे (भिन्न जिनका हरकारक समान है)।

= और =

- = =

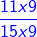
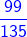
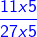
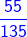
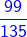
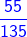
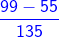
भिन्न का व्युत्क्रम

भिन्न का व्युत्क्रम शीर्ष और नीचले संख्याओं को पलटकर पाया जाता है। उदाहरण के लिए, 2/3 का व्युत्क्रम 3/2 है।

इतिहास की एक झलक

• प्राचीन भारत में, भिन्नों को संस्कृत में भिन्न कहा जाता था, जिसका अर्थ है "टूटा हुआ।" इन्हें भाग या अंश भी कहा जाता था, जो "भाग" या "टुकड़ा" को संदर्भित करता है।
• बक्षाली पांडुलिपि एक प्राचीन ग्रंथ है जिसमें भिन्नों का उल्लेख है, जो लगभग 300 ईस्वी में लिखी गई थी, जो भारत में भिन्नों के ऐतिहासिक उपयोग को दर्शाती है।
• यह तकनीक प्रसिद्ध गणितज्ञों जैसे आर्यभट्ट (लगभग 476–550 ईस्वी), ब्रह्मगुप्त (598–668 ईस्वी), श्रीधराचार्य (लगभग 750 ईस्वी), और महावीराचार्य (लगभग 817-875 ईस्वी) द्वारा उपयोग की गई थी।
• भिन्नों में शीर्षक और हरकारक के बीच एक रेखा खंड का संकेत अल-ख्वारिज़्मी, एक फारसी गणितज्ञ, द्वारा 9वीं शताब्दी में पेश किया गया था।
• भिन्नों का उपयोग प्राचीन संस्कृतियों जैसे मिस्र और बाबेल में भी हुआ, जहाँ मुख्य रूप से भिन्नात्मक इकाइयों का उपयोग किया गया था, जहाँ शीर्षक 1 था। अधिक जटिल भिन्नों को इन इकाइयों के योग के रूप में व्यक्त किया गया, जिसे मिस्री भिन्नें कहा जाता है।
• भारत ने सामान्य भिन्नों (जहाँ शीर्षक हमेशा नहीं होता) को पेश किया, साथ ही जोड़, घटाव, गुणा, और भाग के लिए अंकगणितीय संचालन के नियम भी।
• सुल्ब-सूत्र वेदिक काल से संकेत करते हैं कि भारतीयों ने भिन्नों के साथ काम करने के लिए लंबे समय पहले नियम स्थापित कर लिए थे।
• ब्रह्मगुप्त ने इन नियमों और भिन्नों के लिए विधियों को एक संरचित तरीके से प्रस्तुत किया। उनकी भिन्नों के संचालन की तकनीकें आज भी उपयोग में हैं।
• उदाहरण के लिए, ब्रह्मगुप्त ने नोट किया कि भिन्नों को जोड़ने या घटाने के लिए, आपको उनके हरकारक को समान करना चाहिए। प्रत्येक भिन्न के शीर्षक और हरकारक को दूसरे हरकारक से गुणा करके, फिर शीर्षकों को जोड़ें या घटाएं।
• भारतीय भिन्नों से संबंधित विचार और तरीके अरबों के माध्यम से यूरोप में पहुंचे, जिसने यूरोप में गणित के विकास पर बड़ा प्रभाव डाला।

चलो अभ्यास करें!

प्रश्न 1: पांच गेंदों का कुल वजन 1 किलोग्राम है। यदि वे लगभग समान आकार की हैं, तो प्रत्येक गेंद का वजन क्या होगा?

उत्तर: पांच गेंदों का कुल वजन = 1 किलोग्राम।

इसलिए, प्रत्येक गेंद का वजन = 1/5 किलोग्राम।

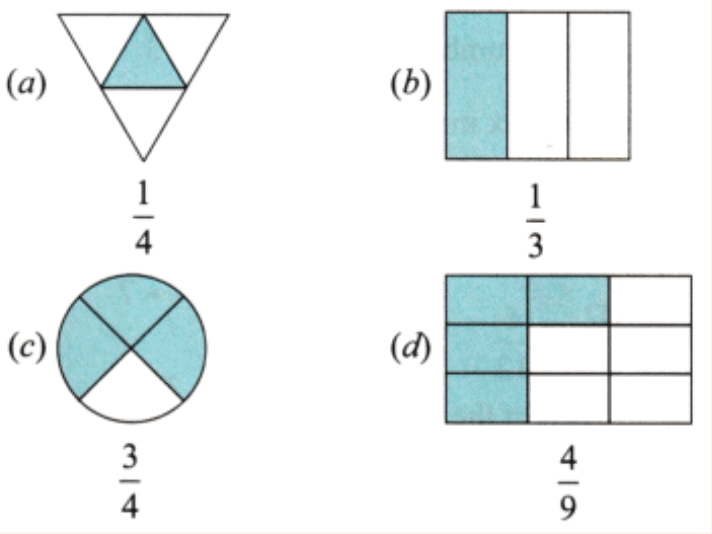
प्रश्न 2: दिए गए भिन्न के अनुसार आकृतियों के भागों को रंग दें।

प्रश्न 2: प्रत्येक भिन्नात्मक इकाई को सही चित्र से मिलाएं।

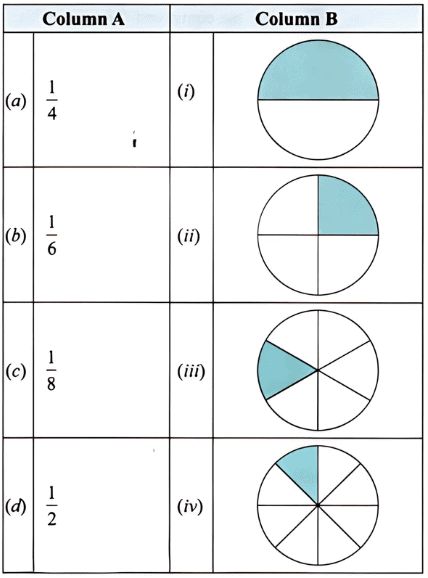
उत्तर: (a) – (ii), (b) – (iii), (c) – (iv), (d) – (i)

प्रश्न 3: निम्नलिखित भिन्नों को मिश्रित भिन्न के रूप में लिखें।

(a) 8/3

(b) 12/7

(c) 25/9

उत्तर:

(a) 8/3 = 2 2/3

(b) 12/7 = 1 5/7

(c) 25/9 = 2 7/9

प्रश्न 4: इन भिन्नों को उचित रूप से जोड़ने या घटाने के रूप में लिखें।

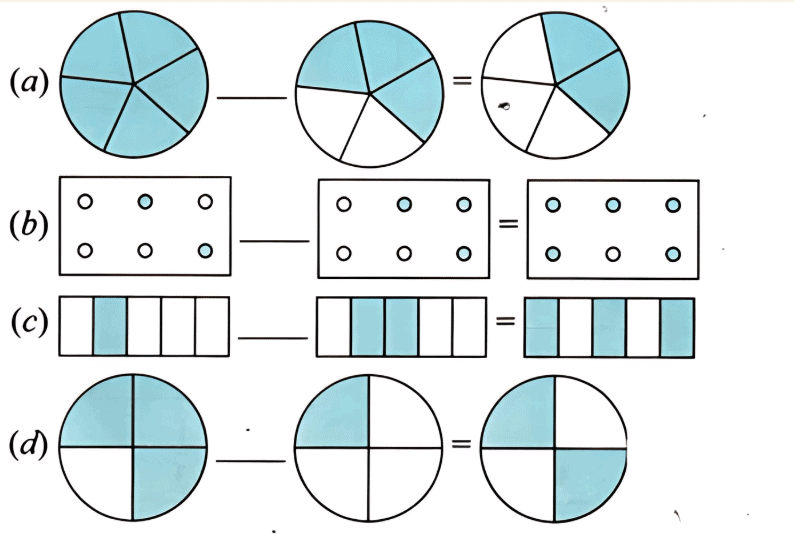
उत्तर:

(a) 5/5 – 3/5 = 2/5

(b) 2/6 + 3/6 = 5/6

(c) 1/5 + 2/5 = 3/5

(d) 3/4 – 1/4 = 2/4

मुख्य बिंदु

• भिन्न एक समान भागों में विभाजित एक संपूर्ण का निर्माण होता है और इसे उचित रूप से साझा किया जाता है।
• भिन्नात्मक इकाइयाँ: संपूर्ण का प्रत्येक समान भाग एक भिन्नात्मक इकाई कहलाती है।
• भिन्न पढ़ना: 5/6 जैसे भिन्न में, 5 को संख्यात्मक और 6 को हर कहा जाता है।
• सही और गलत भिन्न: सही भिन्न में संख्यात्मक हर से छोटा होता है (जैसे, 1/2, 2/3)। गलत भिन्न में संख्यात्मक हर के बराबर या बड़ा होता है (जैसे, 5/4, 6/6)।
• मिश्रित भिन्न: मिश्रित भिन्न में एक संपूर्ण संख्या और एक भिन्न दोनों होते हैं।
• संख्यात्मक रेखा: भिन्नों को संख्यात्मक रेखा पर दर्शाया जा सकता है, जिसमें प्रत्येक भिन्न एक विशेष बिंदु से मेल खाता है।
• समान भिन्न: वे भिन्न जो समान मूल्य या मात्रा दिखाते हैं, उन्हें समान भिन्न कहा जाता है।
• न्यूनतम रूप: एक भिन्न तब न्यूनतम रूप में होता है जब उसके संख्यात्मक और हर में 1 के अलावा कोई सामान्य गुणांक न हो।
• भिन्न का विपरीत: भिन्न का विपरीत प्राप्त करने के लिए इसे संख्यात्मक और हर को स्विच करें।
• भिन्न जोड़ने के लिए ब्रह्मगुप्त का तरीका: भिन्नों को जोड़ने के लिए उन्हें समान हर के साथ समान भिन्नों में बदलें और फिर संख्यात्मक को जोड़ें।
• भिन्न घटाने के लिए ब्रह्मगुप्त का तरीका: भिन्नों को घटाने के लिए उन्हें समान हर के साथ समान भिन्नों में बदलें और फिर संख्यात्मक को घटाएं।