Important Formulas: भिन्न (Fractions) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download
1. भिन्न: एक भिन्न संपूर्ण का एक भाग दर्शाता है। यदि आप किसी चीज़ (जैसे पिज्जा) को समान भागों में बाँटते हैं, तो प्रत्येक भाग को संपूर्ण का एक भिन्न कहा जाता है।
2. भिन्नात्मक इकाई: एक भिन्नात्मक इकाई उस समय संपूर्ण का एक भाग है जब इसे समान भागों में बाँटा गया हो। यह हमें बताती है कि एक भाग संपूर्ण का कितना हिस्सा है। उदाहरण: भिन्न 1/5 में, भिन्नात्मक इकाई 5 समान भागों में से 1 भाग है।
3. भिन्नों का पठन
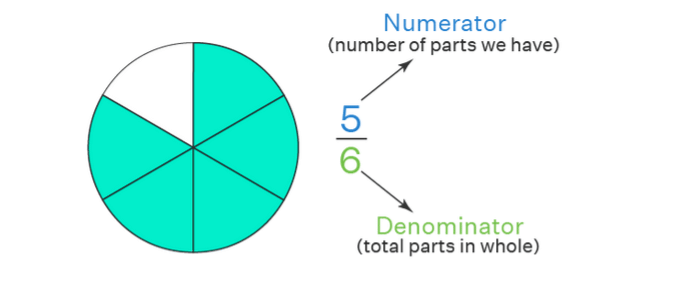
- संख्यात्मक (Numerator): भिन्न के शीर्ष पर संख्या, जो दर्शाती है कि आपके पास कितने भाग हैं।
- हर (Denominator): भिन्न के निचले भाग में संख्या, जो बताती है कि संपूर्ण कितने समान भागों में बाँटा गया है।
4. संख्या रेखा
- एक संख्या रेखा का उपयोग भिन्नों को दिखाने के लिए किया जा सकता है। प्रत्येक भिन्न पूर्ण संख्याओं के बीच एक बिंदु है। 0 और 1 के बीच की दूरी को हर (denominator) के आधार पर समान भागों में बाँटा जाता है।
- उदाहरण: संख्या रेखा पर, 1/2 0 और 1 के बीच का मध्य बिंदु है, जबकि 3/4 1 के करीब है।
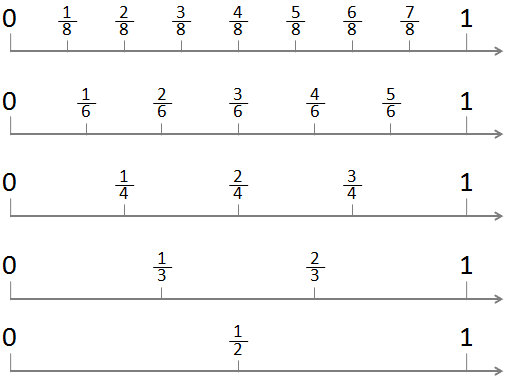
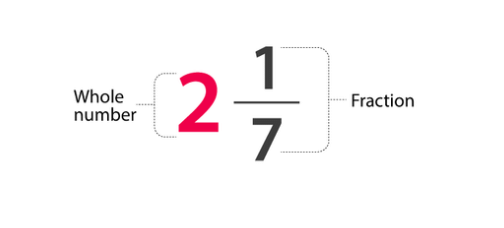
5. मिश्रित भिन्न: एक मिश्रित भिन्न एक पूर्ण संख्या और एक भिन्न का संयोजन होता है।
6. समान भिन्न
- भिन्न जो संपूर्ण का समान भाग दर्शाते हैं लेकिन अलग दिखते हैं, उन्हें समान भिन्न कहा जाता है।
- विधि: समान भिन्न खोजने के लिए, संख्यात्मक और हर (denominator) दोनों को एक ही संख्या से गुणा या भाग करें।
- उदाहरण: 1/2 समान है 2/4 के, क्योंकि यदि आप 1/2 के संख्यात्मक और हर (denominator) को 2 से गुणा करते हैं, तो आपको 2/4 मिलता है।
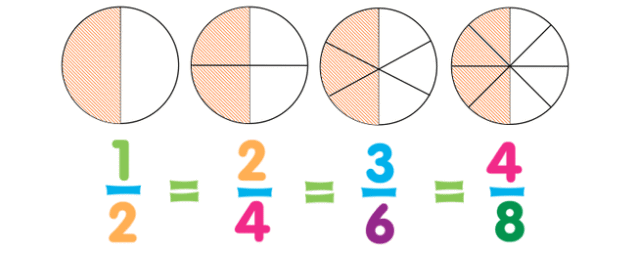
7. सरलतम रूप
- एक भिन्न अपने सरलतम रूप में तब होती है जब संख्यात्मक और हर (denominator) के बीच कोई सामान्य गुणांक 1 के अतिरिक्त न हो।
- विधि: संख्यात्मक और हर (denominator) को उनके सबसे बड़े सामान्य भाजक (GCD) से भाग दें।
- उदाहरण: 6/9 को सरल करने के लिए, दोनों को 3 से भाग दें, तो सरलतम रूप 2/3 है।
8. भिन्नों की तुलना
भिन्नों की तुलना करने की विधि: भिन्नों की तुलना करने के लिए उन्हें समान हर (denominator) में परिवर्तित करें या संख्या रेखा का उपयोग करें।
उदाहरण: 4/5 और 7/9 की तुलना करने के लिए, इन चरणों का पालन करें। हम देख सकते हैं कि 4/5, 7/9 से बड़ा है।
- (i) एक सामान्य हर खोजें:
- यहाँ हर 5 और 9 हैं। 5 और 9 का न्यूनतम समापवर्तक (LCM) 45 है।
- (ii) भिन्नों को परिवर्तित करें:
- 4/5 के अंश और हर को 9 से गुणा करें:
- 7/9 के अंश और हर को 5 से गुणा करें:
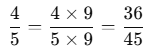
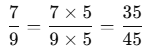
9. समान या भिन्न हर के साथ भिन्नों का जोड़ना:
- यदि हर समान हैं, तो केवल अंशों को जोड़ें।
उदाहरण: 1/4 + 1/4
हल: चूंकि अंश समान हैं, अंश जोड़ें: 1 + 1 = 2, इसलिए उत्तर 2/4 है, जो सरल होकर 1/2 बनता है।

- यदि हर भिन्न हैं, तो न्यूनतम सामान्य हर (LCD) खोजें, फिर अंश जोड़ें।
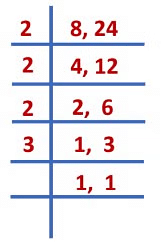
उदाहरण:


8 और 24 का LCM = 2 × 2 × 2 × 3 = 24
अब, हम भिन्नों को समान भिन्नों में परिवर्तित करते हैं। (भिन्नों के हर को 24 में बदलना)
= और



10. समान या भिन्न हर के साथ भिन्नों का घटाना:
- यदि हर समान हैं, तो केवल अंशों को घटाएं।
- यदि हर भिन्न हैं, तो न्यूनतम सामान्य हर (LCD) खोजें, फिर अंश घटाएं।
उदाहरण: 3/4 - 2/4, अंश घटाएं: 3 - 2 = 1, इसलिए उत्तर 1/4 है।

उदाहरण: 8/3 से 4/7 घटाएं।
हल: 4/7 और 8/3 भिन्न हैं क्योंकि उनके हर अलग-अलग हैं। इसलिए, पहले हम 3 और 7 का LCM खोजते हैं।



LCM (3, 7) = 21
8/3 = (8 × 7) / (3 × 7) = 56/21
4/7 = (4 × 3) / (7 × 3) = 12/21
तो, हमारे पास है
8/3 - (4/7)
= 56/21 - (12/21)
= 56/21 - 12/21
= (56 - 12)/21
= 44/21
उत्तर: 8/3 - (4/7) = 44/21















