Worksheet Solutions: निर्माणों के साथ खेलना | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

बहुविकल्पीय प्रश्न

Q1: आप 5 सेमी व्यास के साथ एक सही वृत्त खींचने के लिए कौन सा उपकरण उपयोग करेंगे? (a) स्केल (b) कम्पास (c) सेट स्क्वायर (d) प्रोट्रैक्टर
उत्तर: (b) कम्पास
समाधान: कम्पास को व्यास सेट करके सही वृत्त खींचने के लिए डिज़ाइन किया गया है।

Q2: एक वर्ग में प्रत्येक कोण का माप क्या होता है? (a) 45 डिग्री (b) 60 डिग्री (c) 90 डिग्री (d) 120 डिग्री
उत्तर: (c) 90 डिग्री
समाधान: एक वर्ग में प्रत्येक कोण एक सही कोण होता है, जिसका माप 90 डिग्री होता है।

Q3: जब आप एक आयत खींचते हैं, तो इसके आकर्ण के बारे में निम्नलिखित में से कौन सा सत्य है? (a) वे हमेशा समानांतर होते हैं। (b) वे एक दूसरे को सही कोण पर बिसेक्ट करते हैं। (c) उनकी लंबाई समान होती है। (d) वे एक दूसरे के साथ तीव्र कोण बनाते हैं।
उत्तर: (c) उनकी लंबाई समान होती है।
समाधान: एक आयत के आकर्ण समान लंबाई के होते हैं।

Q4: 6 सेमी की भुजा वाली एक वर्ग खींचने के लिए कम्पास और स्केल का उपयोग करते हुए, पहला कदम क्या होगा? (a) वर्ग का एक पक्ष खींचें। (b) एक आकर्ण खींचें। (c) कम्पास पर 6 सेमी की लंबाई मापें। (d) एक लंबवत बिसेक्टर खींचें।
उत्तर: (a) वर्ग का एक पक्ष खींचें।
समाधान: एक पक्ष खींचकर शुरू करें, फिर इसे अन्य पक्षों के लिए संदर्भ के रूप में उपयोग करें।

Q5: यदि आप दो दिए गए बिंदुओं से समान दूरी पर एक बिंदु खोजना चाहते हैं, तो आप कौन सा उपकरण उपयोग करेंगे? (a) स्केल (b) कम्पास (c) प्रोट्रैक्टर (d) सेट स्क्वायर
उत्तर: (b) कम्पास
समाधान: कम्पास का उपयोग करके दो दिए गए बिंदुओं से समान दूरी पर बिंदुओं को खोजा जा सकता है।

खाली स्थान भरें

Q1: वृत्त के केंद्र से वृत्त के किसी भी बिंदु तक की दूरी को _______ कहा जाता है।
उत्तर: रेशा
समाधान: रेशा वृत्त के केंद्र से वृत्त के परिधि तक की दूरी है।

Q2: सही वृत्त और आर्क खींचने के लिए उपयोग किया जाने वाला उपकरण _______ कहलाता है।
उत्तर: कम्पास
समाधान: कम्पास एक उपकरण है जिसका उपयोग एक बिंदु को फिक्स करके और दूसरे को घुमाकर वृत्त और आर्क खींचने के लिए किया जाता है।

Q3: एक आयत में सभी कोणों का योग _______ डिग्री होता है।
उत्तर: 360
समाधान: एक आयत में चार सही कोण होते हैं, और किसी भी चतुर्भुज में सभी कोणों का योग 360 डिग्री होता है।

Q4: एक वर्ग में _______ समान भुजाएँ और _______ सही कोण होते हैं।
उत्तर: 4, 4
समाधान: एक वर्ग में चार समान लंबाई की भुजाएँ और चार सही कोण होते हैं।

Q5: यदि आप एक रेखा खंड पर एक बिंदु के माध्यम से लंबवत रेखा खींचना चाहते हैं, तो आप आमतौर पर _______ का उपयोग करेंगे।
उत्तर: सेट स्क्वायर या कम्पास
समाधान: लंबवत रेखाएँ खींचने के लिए सेट स्क्वायर या कम्पास का उपयोग किया जाता है।

सत्य/असत्य

प्रश्न 1: एक आयत के सभी भुजाएँ समान लंबाई की होती हैं। उत्तर: असत्य हल: एक आयत में विपरीत भुजाएँ समान लंबाई की होती हैं, लेकिन सन्निकट भुजाएँ भिन्न हो सकती हैं।

प्रश्न 2: एक आयत की विकर्ण हमेशा समान होते हैं। उत्तर: सत्य हल: एक आयत की विकर्ण समान लंबाई की होती हैं, जो समानांतर भुजाओं और समकोणों के गुणों के कारण होती हैं।

प्रश्न 3: यदि एक वर्ग को घुमाया जाए, तो वह तब भी वर्ग ही रहता है जब तक सभी भुजाएँ समान और कोण 90 डिग्री रहें। उत्तर: सत्य हल: एक वर्ग को घुमाने से उसकी विशेषताएँ नहीं बदलतीं; वह वर्ग ही बना रहता है।

प्रश्न 4: वह बिंदु जहाँ एक आयत के दो विकर्ण मिलते हैं, विकर्णों को दो समान भागों में विभाजित करता है। उत्तर: सत्य हल: एक आयत के विकर्ण एक-दूसरे को आधा करते हैं, जिससे दो समान खंड बनते हैं।

प्रश्न 5: बिना पैमाने के, एक कंपास का उपयोग करके भुजा की लंबाई मापी जा सकती है। उत्तर: सत्य हल: एक कंपास का उपयोग एक भुजा से दूसरी भुजा पर माप स्थानांतरित करने के लिए किया जा सकता है बिना पैमाने की आवश्यकता के।

व्यावहारिक अनुप्रयोग प्रश्न

प्रश्न 1: एक कंपास और पैमाने का उपयोग करके 5 सेमी की भुजा लंबाई वाला एक वर्ग बनाएं। निर्देश:

• एक पैमाने का उपयोग करके 5 सेमी की सीधी रेखा खींचें। अंत बिंदुओं को A और B के रूप में चिह्नित करें।
• कंपास का बिंदु A पर रखें, इसे 5 सेमी के व्यास पर सेट करें, और एक आर्क बनाएं।
• कंपास की चौड़ाई को बदले बिना, कंपास का बिंदु B पर रखें और एक और आर्क बनाएं जो पहले आर्क को काटता है। चौराहे को बिंदु C के रूप में चिह्नित करें।
• A से C और B से C तक रेखाएँ खींचें।
• चरण 2-4 को दोहराएं ताकि बिंदु D को C के विपरीत खोजा जा सके, A से D और B से D को जोड़कर वर्ग पूरा करें।

उत्तर: हल: यह सुनिश्चित करके कि वर्ग की प्रत्येक भुजा 5 सेमी है और रेखाओं को सही ढंग से जोड़कर, जो आकृति बनेगी वह एक वर्ग होगी।

प्रश्न 2: 4 सेमी और 6 सेमी की भुजाओं वाला एक आयत बनाएं। सत्यापित करें कि क्या विकर्ण समान हैं। निर्देश:

प्रश्न 1: 6 सेमी लंबाई का एक रेखाखंड खींचें और इसे AB के रूप में चिह्नित करें।

• बिंदु A और B पर, एक सेट स्क्वायर या कंपास का उपयोग करके लंबवत रेखाएँ खींचें।
• बिंदु A से, लंबवत रेखा के साथ 4 सेमी मापें और इसे बिंदु D के रूप में चिह्नित करें।
• बिंदु B से, लंबवत रेखा के साथ 4 सेमी मापें और इसे बिंदु C के रूप में चिह्नित करें।
• बिंदु C और D को जोड़कर आयत ABCD पूरा करें।
• एक पैमाने का उपयोग करके AC और BD विकर्ण खींचें।

उत्तर: AC और BD मापें; दोनों विकर्ण लगभग 7.21 सेमी में समान होने चाहिए। समाधान: एक आयत में, विकर्ण हमेशा समान होते हैं। मापने से छात्र यह पुष्टि करते हैं कि AC = BD।

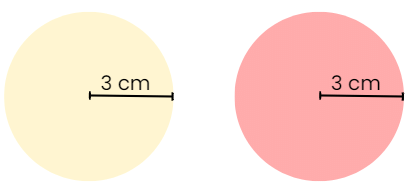
प्रश्न 2: कंपास का उपयोग करके 3 सेमी त्रिज्या वाला एक वृत्त खींचें। फिर, उसी त्रिज्या के साथ लेकिन विभिन्न केंद्र के साथ दूसरा वृत्त खींचें। निर्देश:

• कंपास को 3 सेमी की त्रिज्या पर सेट करें।
• कंपास का बिंदु पेपर पर एक चुने हुए बिंदु (O) पर रखें और पहला वृत्त खींचें।
• O से कम से कम 6 सेमी दूर एक और बिंदु (P) चुनें।
• P पर कंपास का बिंदु रखें और उसी 3 सेमी त्रिज्या के साथ दूसरा वृत्त खींचें।

उत्तर: छात्र के पास समान त्रिज्या के साथ लेकिन विभिन्न केंद्रों वाले दो वृत्त होने चाहिए। समाधान: वृत्त समकोण हैं, क्योंकि दोनों की त्रिज्या 3 सेमी है, भले ही उनके केंद्र भिन्न हों।

प्रश्न 3: एक डॉट ग्रिड पर एक आयत खींचें और इसके विकर्ण खींचें। विकर्णों के प्रतिच्छेदन द्वारा बनाए गए कोणों को मापें। निर्देश:

• ग्रिड पर चार डॉट्स चुनें ताकि वे एक आयत के शीर्षकों को बनाएं। उन्हें A, B, C, और D के रूप में चिह्नित करें।
• डॉट्स को जोड़कर आयत ABCD बनाएं।
• AC विकर्ण को A से C और BD विकर्ण को B से D जोड़कर खींचें।
• विकर्णों के प्रतिच्छेद बिंदु (O) पर बने कोणों को मापें।

उत्तर: यदि आयत ग्रिड के साथ पूरी तरह से संरेखित है, तो प्रतिच्छेदन पर बने सभी कोण 90 डिग्री के बराबर होंगे। समाधान: एक आयत में, विकर्ण एक-दूसरे को आधा करते हैं, और प्रतिच्छेदन पर बने कोण समकोण होते हैं (90 डिग्री)।

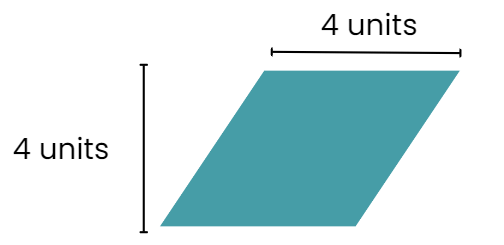
प्रश्न 4: एक चार-तरफा आकृति बनाएं जहाँ सभी भुजाएँ समान हों, लेकिन यह एक वर्ग नहीं है। उस आकृति को क्या कहते हैं? निर्देश:

• 5 सेमी की एक रेखा खींचें और उसे AB के रूप में लेबल करें।
• कंपास को 5 सेमी पर सेट करें और बिंदुओं A और B से आर्क खींचें ताकि बिंदु C और D का पता लगाया जा सके, इस तरह कि AC = BD = 5 सेमी।
• C और D बिंदुओं को जोड़ने के लिए कंपास को 90 डिग्री से कम के कोण पर समायोजित करें।
• सभी बिंदुओं (ABCD) को जोड़ें ताकि आकृति पूरी हो जाए।

उत्तर: जो आकृति बनी है वह एक रोम्बस है। समाधान: एक रोम्बस के सभी किनारे समान लंबाई के होते हैं, लेकिन एक वर्ग के विपरीत, इसके कोण 90 डिग्री नहीं होते, जिससे इसका एक विशेष झुका हुआ आकार होता है।