निर्माणों के साथ खेलना Chapter Notes | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

परिचय

कल्पना कीजिए कि आप केवल एक स्केल और एक कम्पास का उपयोग करके सही आकृतियाँ बना सकते हैं! इस अध्याय में, आप ज्यामिति के विशेषज्ञ बन जाएंगे क्योंकि आप वृत्त, वर्ग, आयत और अन्य रोचक आकृतियाँ बनाना सीखेंगे। चरण-दर-चरण, आप इन निर्माणों के रहस्यों का पता लगाएंगे और देखेंगे कि कैसे सरल उपकरण आपकी डिज़ाइन को सटीक बनाने में मदद कर सकते हैं। इस अध्याय के अंत तक, आपके पास आत्मविश्वास के साथ इन आकृतियों को अपने आप बनाने की कौशल होगा। तो, ज्यामिति के जादू की खोज के लिए तैयार हो जाइए!

कला कार्य

फ्रीहैंड आकृतियाँ बनाने का तरीका समझें और फिर ज्यामितीय उपकरणों का उपयोग करके इन आकृतियों को अधिक सटीकता से पुनः बनाएं।

मुख्य अवधारणाएँ

• वक्र और रेखाएँ: वक्र में कोई भी आकृति शामिल होती है जिसे कागज पर बनाया जा सकता है, जैसे सीधे रेखाएँ, वृत्त, और अन्य आकृतियाँ।
• कम्पास का उपयोग: एक कम्पास का उपयोग वृत्त और आर्क बनाने के लिए किया जाता है। एक बिंदु को चिह्नित करके और कम्पास को एक विशेष लंबाई पर समायोजित करके, हम उस बिंदु को केंद्र मानकर एक वृत्त बना सकते हैं।

उदाहरण

अपने नोटबुक पर एक बिंदु चिह्नित करें।

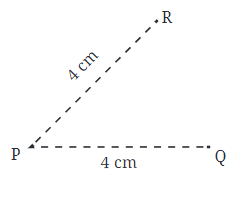
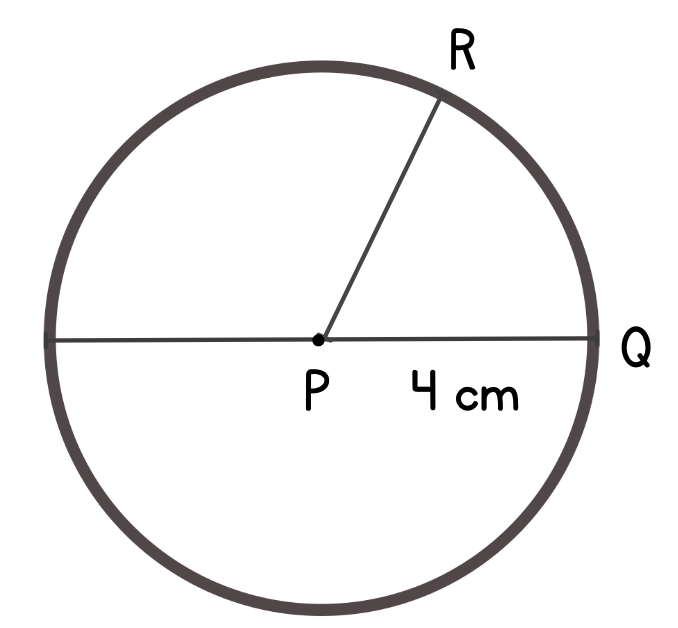
अब, एक कम्पास का उपयोग करके P से 4 सेमी की दूरी पर विभिन्न दिशाओं में बिंदु चिह्नित करें। इन बिंदुओं को जोड़कर एक वृत्त बनाएं। यहाँ, 'P' केंद्र है, और दूरी (4 सेमी) वृत्त की त्रिज्या है।

वर्ग और आयतें

आयत को समझना

• आयत ABCD: चलिए एक आयत ABCD पर ध्यान केंद्रित करते हैं।
• कोने और भुजाएँ: बिंदु A, B, C, और D आयत के कोने हैं। रेखाएँ AB, BC, CD, और DA इसकी भुजाएँ हैं। इन कोनों के कोणों को ∠A, ∠B, ∠C, और ∠D कहा जाता है।
• विपरीत भुजाएँ: भुजाएँ AB और CD को विपरीत भुजाएँ कहा जाता है क्योंकि वे एक-दूसरे के सामने होती हैं। इसी प्रकार, AD और BC भी एक अन्य जोड़ी की विपरीत भुजाएँ बनाती हैं।

आयत के गुण

• विपरीत भुजाएँ: एक आयत में, विपरीत भुजाएँ लंबाई में समान होती हैं।
• कोण: आयत के सभी कोण 90 डिग्री होते हैं।

आयत का नामकरण

• चित्र में आयत का नाम ABCD है, लेकिन इसे BCDA, CDAB, DABC, ADCB, DCBA, CBAD, और BADC भी कहा जा सकता है।

वैध नामकरण

• एक आयत को कोने के लेबल के किसी भी संयोजन का उपयोग करके नामित किया जा सकता है, लेकिन सभी संयोजन अनुमत नहीं हैं।
• उदाहरण के लिए, नाम जैसे ABDC या ACBD वैध नहीं हैं।
• एक वैध नाम को उस क्रम में कोनों को सूचीबद्ध करना चाहिए जिसमें आप आयत के चारों ओर यात्रा करते हैं, किसी भी कोने से शुरू करते हुए।

वर्ग को समझना

जैसे एक आयत में, एक वर्ग के कोने और किनारे उसी प्रकार परिभाषित होते हैं।

एक वर्ग की विशेषताएँ: एक वर्ग की दो प्रमुख विशेषताएँ हैं:

• सभी किनारे समान लंबाई के होते हैं।
• सभी कोण 90 डिग्री होते हैं।

घूमते हुए वर्ग और आयत

जब हम एक वर्ग के कागज के टुकड़े को घुमाते हैं, तो हम देखना चाहते हैं कि क्या यह अभी भी एक वर्ग बना रहता है।

आइए विशेषताओं की जांच करें:

• क्या सभी किनारे अभी भी समान हैं? हाँ, वे हैं।
• क्या सभी कोण अभी भी 90 डिग्री हैं? हाँ, वे हैं।

एक वर्ग को घुमाने से उसके किनारों की लंबाई या उसके कोणों के माप में परिवर्तन नहीं होता है। चूंकि घुमाया गया आकृति अभी भी वर्ग की विशेषताओं को पूरा करता है, यह अभी भी एक वर्ग है।

इसी प्रकार, जब हम एक आयत को घुमाते हैं, तो यह उसी कारणों से एक आयत बनी रहती है।

वर्ग और आयत बनाना वर्ग और आयत हमारे चारों ओर हैं! इस भाग में, हम उन्हें एक रूलर और कंपास की मदद से सटीकता से कैसे खींचना सीखेंगे। सरल चरणों के साथ, हम सही किनारे और सही कोण सुनिश्चित करेंगे। आइए शुरू करते हैं!

वर्ग और आयत के निर्माण को समझें उदाहरण की मदद से

6 सेमी की भुजा लंबाई वाला वर्ग कैसे बनाएं?

6 सेमी लंबाई वाले प्रत्येक किनारे वाला वर्ग बनाने के लिए इन चरणों का पालन करें:

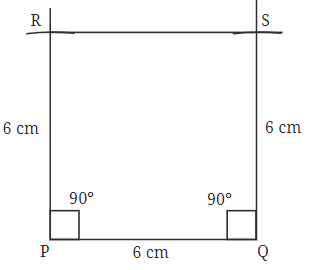
चरण 1: 6 सेमी भुजा लंबाई वाला वर्ग PQRS बनाएं।

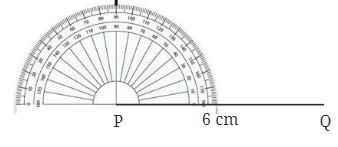
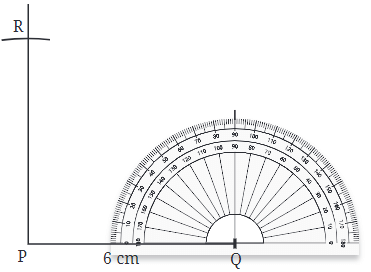
चरण 2: बिंदु P पर, PQ के लिए एक लंबवत रेखा खींचें।

चरण 3: विधि 1: एक रूलर का उपयोग करते हुए, लंबवत रेखा पर बिंदु S को इस प्रकार चिह्नित करें कि PS = 6 सेमी।

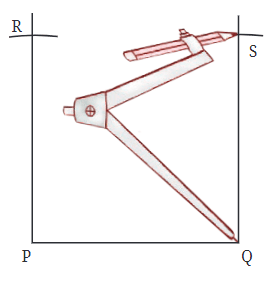
विधि 2: आप PS को मापने के लिए कंपास का भी उपयोग कर सकते हैं।

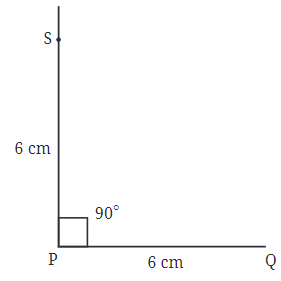
चरण 4: PQ रेखा खंड पर बिंदु Q पर एक लंबवत रेखा खींचें।

चरण 5: यदि कंपास का उपयोग कर रहे हैं, तो अगला बिंदु इसे आसानी से चिह्नित किया जा सकता है।

चरण 6: सुनिश्चित करें कि सभी किनारे समान हैं और वर्ग को पूरा करें।

आयतों में अन्वेषण

एक आयत एक चार-तरफा आकृति होती है जहाँ विपरीत पक्षों की लंबाई समान होती है, और चारों कोण सही कोण (90 डिग्री) होते हैं। कल्पना करें कि आपके पास एक आयत के आकार का कागज है। लंबे पक्षों को आमतौर पर लंबाई कहा जाता है, और छोटे पक्षों को चौड़ाई कहा जाता है।

उदाहरणों के साथ समझना

आयत ABCD खींचें जहाँ पक्ष AB = 7 सेमी और पक्ष BC = 4 सेमी है।

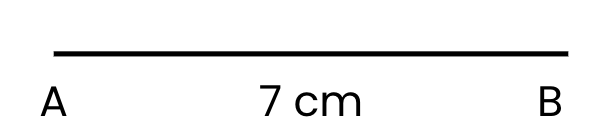
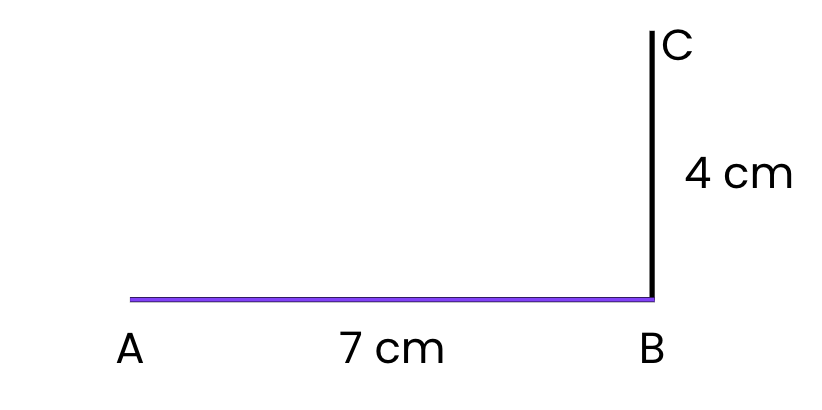
चरण 1: पक्ष AB (7 सेमी) खींचें:

• अपने स्केल का उपयोग करके एक सीधी क्षैतिज रेखा खींचें।
• शुरुआत पर बिंदु A और 7 सेमी पर बिंदु B को चिह्नित करें। यह पक्ष AB = 7 सेमी है।

चरण 2: पक्ष BC (4 सेमी) खींचें:

• बिंदु B से, अपने स्केल का उपयोग करके एक ऊर्ध्वाधर रेखा ऊपर की ओर खींचें।
• 4 सेमी मापें और बिंदु C को चिह्नित करें। यह पक्ष BC = 4 सेमी है।

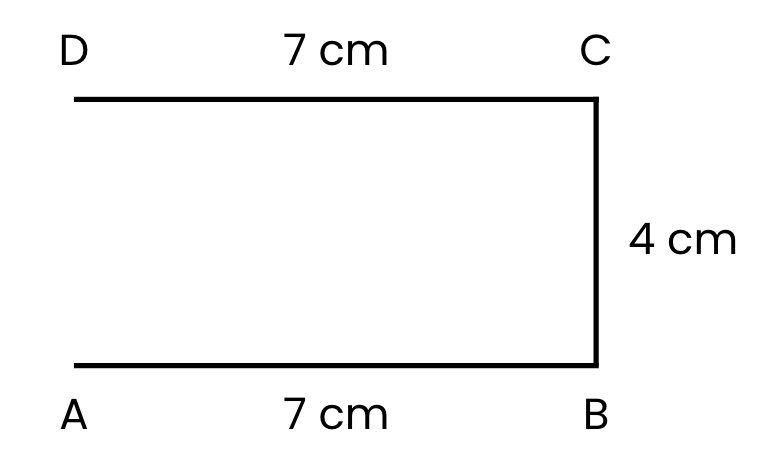
चरण 3: पक्ष CD (7 सेमी) खींचें:

• बिंदु C से, पक्ष AB के समानांतर एक क्षैतिज रेखा खींचें।
• 7 सेमी मापें और बिंदु D को चिह्नित करें। यह पक्ष CD = 7 सेमी है।

चरण 4: पक्ष DA (4 सेमी) खींचें:

• अंततः, बिंदु D को बिंदु A से ऊर्ध्वाधर रेखा से जोड़ें।
• यह सुनिश्चित करने के लिए 4 सेमी मापें कि यह पक्ष BC के समान लंबाई है। यह पक्ष DA = 4 सेमी है।

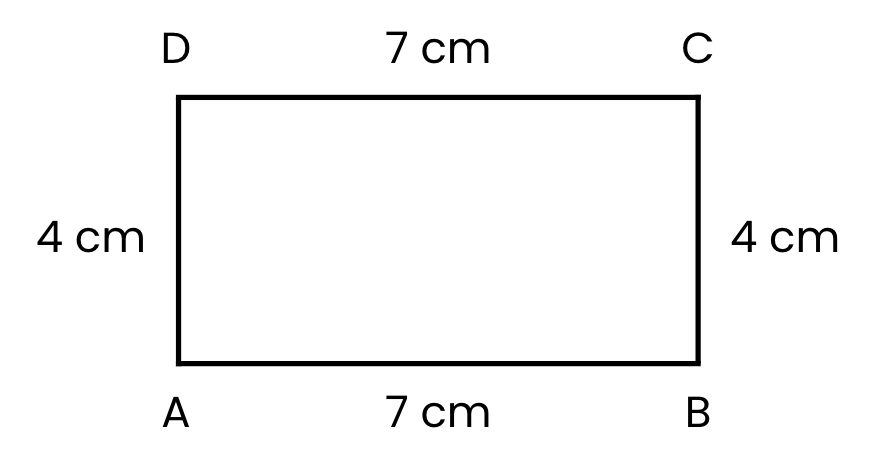
चरण 5: आयत को लेबल करें:

• प्रत्येक कोने पर A, B, C, और D के अक्षर लिखें।
• आपने अब आयत ABCD खींची है जिसमें AB = 7 सेमी और BC = 4 सेमी है!

गतिविधि:

आइए एक आयत में बिंदु X और Y के बारे में जानें और उनके बीच की दूरी कैसे मापें!

चरण 1: बिंदु X और Y

• कल्पना करें कि आपका आयत ABCD एक खेल का मैदान है। पक्ष AD एक सीमा है, और पक्ष BC विपरीत सीमा है। बिंदु X एक छोटी चींटी की तरह है जो पक्ष AD (A से D तक) पर चल सकती है। बिंदु Y एक और चींटी है जो पक्ष BC (B से C तक) पर चल सकती है।
• X और Y कहाँ हो सकते हैं? बिंदु X A, D पर या पक्ष AD के बीच कहीं भी हो सकता है। बिंदु Y B, C पर या पक्ष BC के बीच कहीं भी हो सकता है।

चरण 2: XY की दूरी मापना

• अब, चलिए X और Y के बीच की दूरी मापते हैं। एक स्केल का उपयोग करके X और Y को जोड़ने वाली एक सीधी रेखा खींचें। इस रेखा को XY कहा जाता है। अपने स्केल का उपयोग करके XY की लंबाई मापें।
• जब आप X और Y को हिलाते हैं तो क्या होता है? यदि X A पर है और Y B पर है, तो XY की दूरी आयत की ऊँचाई (4 सेमी) के बराबर होगी। यदि X D पर है और Y C पर है, तो XY की दूरी भी 4 सेमी होगी। यदि X और Y AD और BC के बीच कहीं हैं, तो XY की दूरी फिर भी 4 सेमी होगी।

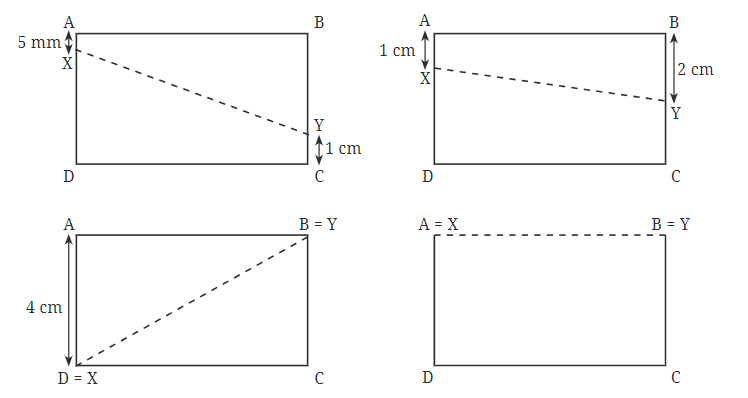
मुख्य अवलोकन: सबसे छोटी दूरी

• चाहे X और Y पक्ष AD और BC पर कहीं भी हों, उनके बीच की सबसे छोटी दूरी हमेशा 4 सेमी होगी। इसका कारण यह है कि X और Y के बीच की सबसे छोटी पंक्ति AB और DC के समानांतर होती है।

आयतों और वर्गों के विकर्णों का अन्वेषण विकर्ण विशेष रेखाएँ होती हैं जो आकृति के विपरीत कोनों को जोड़ती हैं। इस अनुभाग में, हम वर्गों और आयतों में विकर्ण खींचने और मापने के तरीके की खोज करेंगे और उनकी अद्वितीय विशेषताओं को समझेंगे।

कोण और विकर्ण

जब आप एक विकर्ण खींचते हैं, तो यह कोने के कोणों को दो छोटे कोणों में विभाजित करता है। उदाहरण के लिए, यदि हमारे पास कोने P और R के साथ एक आयत है, तो विकर्ण विभाजित करता है:

• कोण P को दो कोणों में विभाजित करें
• कोण R को दो कोणों में विभाजित करें

क्या आपको लगता है कि c = d और g = h? उन्हें मापने की कोशिश करें और जांचें।

वर्ग के बारे में क्या?

वर्ग एक विशेष आयत है जहाँ चारों भुजाएँ समान होती हैं। एक वर्ग में:

• आड़ा रेखाएँ (diagonals) अब भी समान होती हैं
• आड़ा रेखाएँ एक-दूसरे को ठीक आधे में काटती हैं
• वे केंद्र पर दाईं कोण (right angles) (90°) भी बनाती हैं

रोचक अवलोकन

• कोई फर्क नहीं पड़ता कि आयत कितनी बड़ी या छोटी है, आड़ा रेखाएँ हमेशा समान होती हैं।
• एक वर्ग में, आड़ा रेखाओं की और भी दिलचस्प विशेषताएँ होती हैं।

आपके लिए चुनौती

क्या आप एक आयत बना सकते हैं और मापने से पहले यह अनुमान लगा सकते हैं कि कोण कैसे विभाजित होंगे? आइए देखते हैं कि क्या आप एक आड़ा रेखा जासूस हैं।

उदाहरणों के माध्यम से समझना

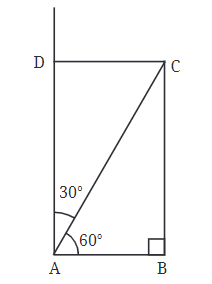
उदाहरण 1: विशेष कोणों के साथ आयत बनाना मान लीजिए हम एक आयत बनाना चाहते हैं जहाँ एक कोने को 60° और 30° के कोणों में विभाजित किया गया है।

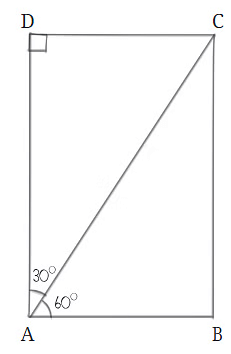
चरण 1: हम एक आधार रेखा खींच सकते हैं, जिसे हम AB कहेंगे। यह रेखा किसी भी लंबाई की हो सकती है जिसे हम चुनें।

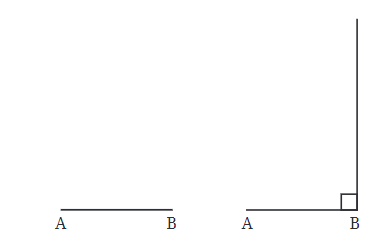
चरण 2: अगला, हमें बिंदु C को खोजना है। इसके लिए, हम बिंदु B से एक रेखा खींचते हैं जो सीधे ऊपर जाती है, AB के साथ एक दाईं कोण बनाती है। यह हमें बिंदु C खोजने में मदद करता है, जो इस रेखा पर कहीं होना चाहिए।

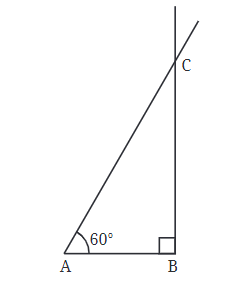
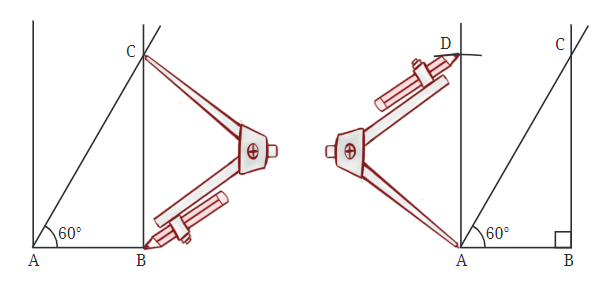
चरण 3: अब, हमें बिंदु A पर कोण बनाने की आवश्यकता है। हमें पता है कि एक कोण 60° होना चाहिए, इसलिए हम वह कोण खींच सकते हैं। दूसरा कोण 90° का कुल बनाने के लिए जो बचता है, वह होगा क्योंकि आयत के सभी कोने दाईं कोण होते हैं।

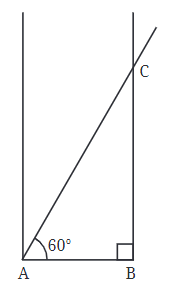
चरण 4: जब हमारे पास बिंदु D हो, तो हम बिंदुओं को जोड़कर आयत पूरा कर सकते हैं। हम बिंदुओं D और B से लंबवत रेखाएँ खींचकर अंतिम कोने खोज सकते हैं, या हम यह तथ्य इस्तेमाल कर सकते हैं कि आयत के विपरीत भुजाएँ समान होती हैं, ताकि हम खोए हुए बिंदु को खोज सकें।

चरण 5: अंत में, हम यह सुनिश्चित करने के लिए जांचते हैं कि हमारा आयत सही दिखाई दे रहा है। यदि आवश्यक हो, तो हम समायोजन कर सकते हैं, लेकिन यह एक निश्चित कोण के साथ आयत बनाने का मूल विचार है!

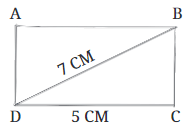
उदाहरण 2: दिए गए भुजा और विकर्ण के साथ आयत बनाना। कभी-कभी, हमें एक आयत बनानी होती है जब हमें एक भुजा की लंबाई और विकर्ण ज्ञात होता है। मान लीजिए कि एक भुजा 5 सेमी लंबी है और विकर्ण 7 सेमी लंबा है।

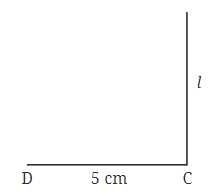
चरण 1: हम आयत के आधार को खींचने से शुरू करते हैं, जिसे CD कहा जाता है, जो 5 सेमी लंबा है।

चरण 2: अगला, हमें बिंदु C से सीधा ऊपर एक रेखा खींचनी है। यह रेखा हमें बिंदु B खोजने में मदद करेगी, जो इस रेखा पर किसी स्थान पर होना चाहिए।

चरण 3: अब, हमें बिंदु B खोजना है। हमें पता है कि B बिंदु D से 7 सेमी दूर होना चाहिए। B का अनुमान लगाने के बजाय, हम बिंदु D के चारों ओर 7 सेमी त्रिज्या वाली एक वृत्त खींच सकते हैं। वह बिंदु जहां यह वृत्त बिंदु C से ऊपर जा रही रेखा को काटता है, वह बिंदु B होगा।

चरण 4: जब हमारे पास बिंदु C, D, और B हो जाते हैं, तो हम अंतिम कोने, बिंदु A को खोजकर आयत को पूरा कर सकते हैं। हम बिंदु D और B से सीधी रेखाएँ खींचकर ऐसा करते हैं जो एक-दूसरे से मिलती हैं।

इस उदाहरण में, लंबवत बिसेक्टर वह रेखा होगी जो बिंदु B और C के बीच के मध्य से सीधे नीचे चलती है, यह दिखाते हुए कि सभी बिंदु दोनों से समान दूरी पर हैं।

दो दिए गए बिंदुओं से समान दूरी पर बिंदु

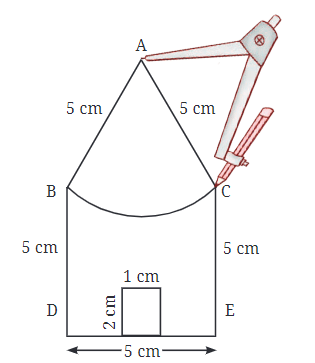
हम एक दिलचस्प विचार का उपयोग करके चरण दर चरण एक घर के आकार का निर्माण करना सीखेंगे—दो दिए गए बिंदुओं से समान दूरी (समान दूरी) पर बिंदुओं को खोजना।

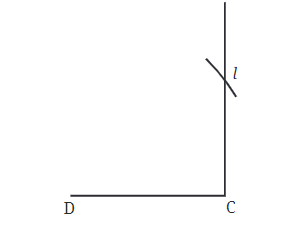
चरण 1: आधार संरचना बनाना

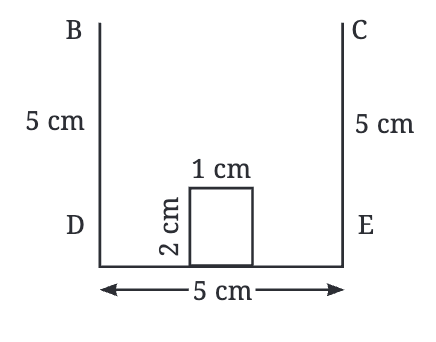
• पहले, हम 5 सेमी चौड़ा और 5 सेमी ऊँचा एक आयत बनाते हैं।
• इस आयत के अंदर, हम 1 सेमी चौड़ाई और 2 सेमी ऊँचाई का एक छोटा दरवाजा भी बनाते हैं।
• तो अब, हमारे घर की दीवारें और दरवाजा तैयार हैं। लेकिन हमें अभी भी छत की आवश्यकता है!

चरण 2: छत की चोटी का पता लगाना (बिंदु A)

• छत की चोटी (बिंदु A) बिंदु B और C (आयत के शीर्ष कोनों) से 5 सेमी दूर होनी चाहिए।
• इस बिंदु को सही ढंग से खोजने के लिए, हम सीधे मापने के बजाय कम्पास का उपयोग कर सकते हैं।
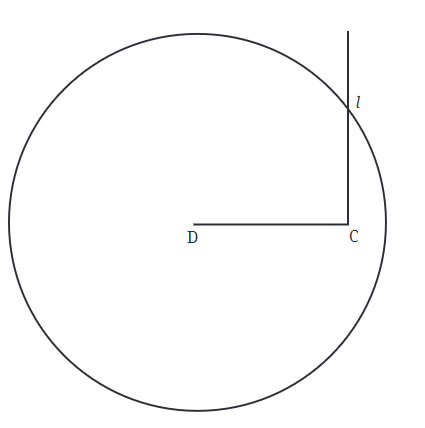
• पहले, कम्पास को बिंदु B पर रखकर 5 सेमी रेडियस के साथ एक वृत्त बनाएं।
• इसका मतलब है कि इस वृत्त पर प्रत्येक बिंदु B से ठीक 5 सेमी दूर है। लेकिन हमें एक ऐसा बिंदु चाहिए जो C से भी 5 सेमी दूर हो।

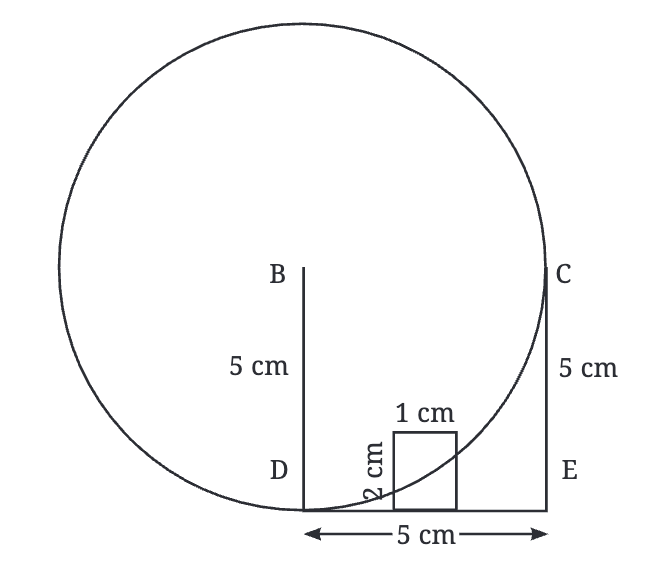
चरण 3: A का सटीक स्थान खोजना

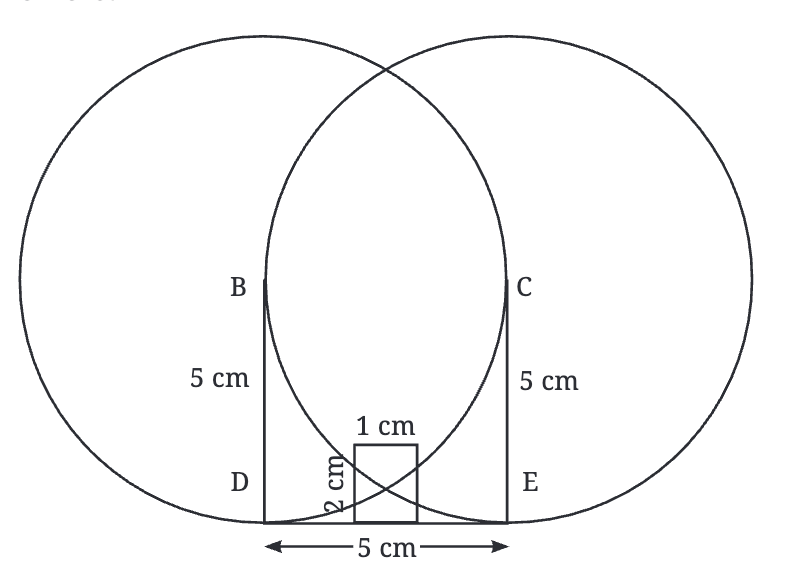
• अब, कम्पास को बिंदु C पर रखकर 5 सेमी रेडियस का एक और वृत्त बनाएं।
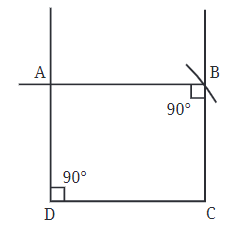
• दो वृत्त दो बिंदुओं पर मिलते हैं।
• आयत के ऊपर का बिंदु हमारे छत की चोटी (बिंदु A) है!
• लंबवत बिसेक्टर बनाएं: दोनों मिलन बिंदुओं को एक सीधी रेखा से जोड़ें।
• यह रेखा सभी बिंदुओं का प्रतिनिधित्व करती है जो B और C से समान दूरी पर हैं।
• वैकल्पिक विधि: बिंदु A को B और C से 5 सेमी के रेडियस के आर्क बनाकर भी प्राप्त किया जा सकता था।
• A को B और A को C के साथ सीधी रेखाओं की मदद से जोड़ें।

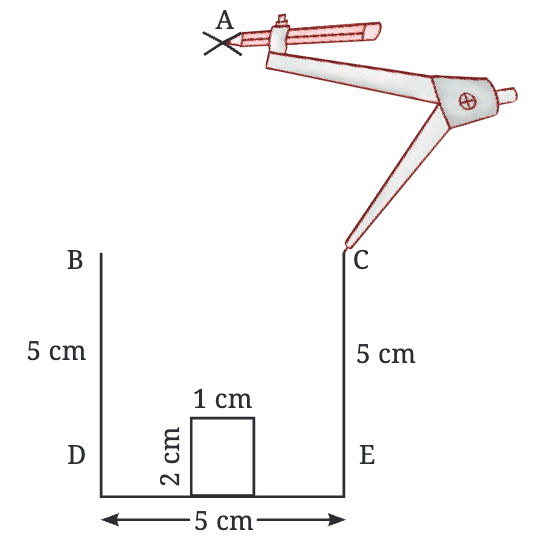
चरण 4: अंतिम चरण:

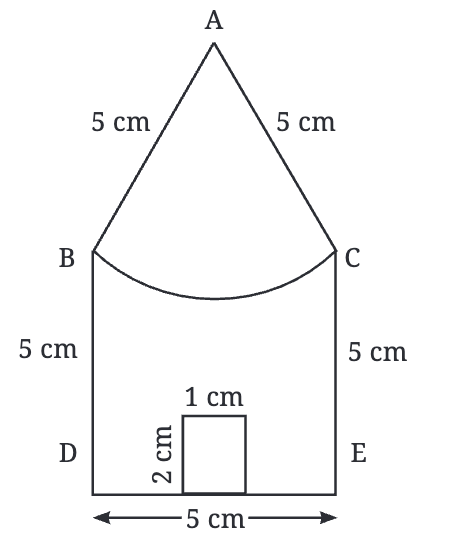
• एक सर्कल के सभी बिंदु इसके केंद्र से समान दूरी पर होते हैं। इस दूरी को सर्कल की त्रिज्या कहा जाता है।
• एक कम्पास का उपयोग सर्कल और उनके भागों को बनाने के लिए किया जा सकता है।
• एक मोटा चित्र यह योजना बनाने में सहायक हो सकता है कि किस प्रकार एक दिए गए आकार का निर्माण किया जाए।
• एक आयत को उसके किनारों की लंबाई या एक किनारे और एक विकर्ण की लंबाई दी गई होने पर बनाया जा सकता है।

मुख्य बिंदु

• एक सर्कल के सभी बिंदु इसके केंद्र से समान दूरी पर होते हैं। इस दूरी को सर्कल की त्रिज्या कहा जाता है।
• एक कम्पास का उपयोग सर्कल और उनके भागों को बनाने के लिए किया जा सकता है।
• एक मोटा चित्र यह योजना बनाने में सहायक हो सकता है कि किस प्रकार एक दिए गए आकार का निर्माण किया जाए।
• एक आयत को उसके किनारों की लंबाई या एक किनारे और एक विकर्ण की लंबाई दी गई होने पर बनाया जा सकता है।