निर्माण के साथ खेलना NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

पृष्ठ 190

निर्माण

प्रश्न 1: एक व्यक्ति, आप इसे कैसे बनाएंगे? इस चित्र में दो घटक हैं। आप पहले भाग को बनाने का तरीका समझ गए होंगे। दूसरे भाग को बनाने के लिए इसे देखें। यहाँ चुनौती यह है कि आप कम्पास के टिप को कहाँ रखना है और इस वक्र को बनाने के लिए किस त्रिज्या का उपयोग करना है। आप कम्पास में एक त्रिज्या तय कर सकते हैं और विभिन्न स्थानों पर कम्पास के टिप को रखकर देख सकते हैं कि कौन सा बिंदु वक्र प्राप्त करने के लिए काम करता है। अपने अनुमान का उपयोग करके तय करें कि टिप कहाँ रखनी है।

उत्तर:

चरण 1: हम चित्र के आधार से शुरू करते हैं। हम 4 सेमी लंबी एक रेखा AB को आधार के रूप में लेते हैं। (चित्र 1)

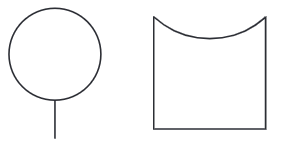
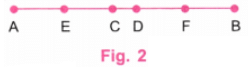
चरण 2: A और B पर, प्रोट्रैक्टर का उपयोग करके लंबवत रेखाएं खींचें। (चित्र 2)

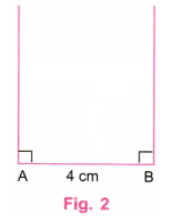
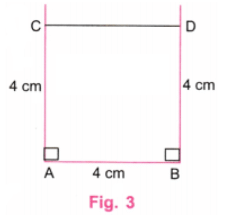
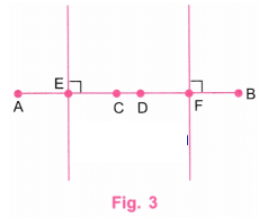
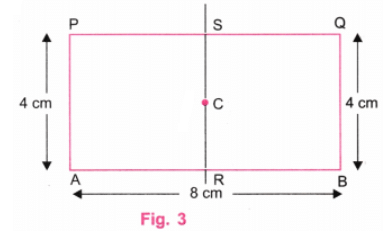
चरण 3: शासक का उपयोग करते हुए, C और D बिंदुओं को इस प्रकार चिह्नित करें कि AC = 4 सेमी और BD = 4 सेमी। C और D को एक रेखा द्वारा जोड़ें। (चित्र 3)

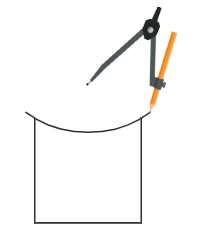
चरण 4: शासक का उपयोग करके, CD पर M बिंदु इस प्रकार लें कि CM = 2 सेमी। M, CD का मध्य बिंदु है। प्रोट्रैक्टर का उपयोग करके, M पर CD के लिए लंबवत रेखा खींचें। इस लंबवत पर एक बिंदु P लें ताकि PM = 2 सेमी हो। PM की दूरी 2 सेमी से थोड़ी कम या अधिक भी हो सकती है। (चित्र 4)

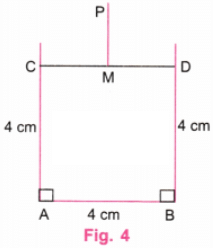
चरण 5: PD को जोड़ें। P के केंद्र पर, D से C तक PD के बराबर त्रिज्या से एक आर्क बनाएं। P के केंद्र पर, 1.5 सेमी की त्रिज्या से एक वृत्त बनाएं। PM को आर्क को छूने के लिए बढ़ाएं। (चित्र 5)

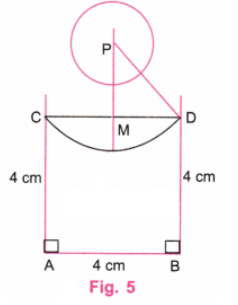
चरण 6: चित्र 5 में अतिरिक्त रेखाओं को चित्र 6 के अनुसार मिटा दें।

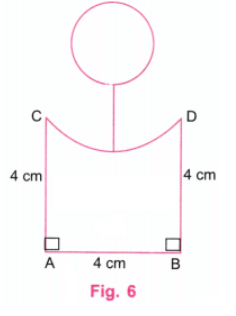
चरण 7: चित्र 6 में दिए गए “एक व्यक्ति” का आवश्यक चित्रण प्रदर्शित किया गया है।

पृष्ठ 191

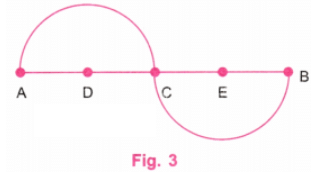
प्रश्न 2: लहराती लहर, इसे बनाएं।

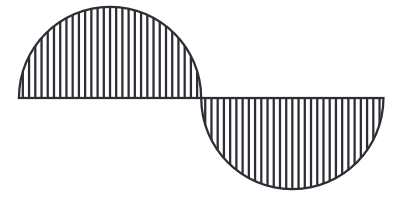
चूंकि केंद्रीय रेखा की लंबाई निर्दिष्ट नहीं की गई है, हम इसे किसी भी लंबाई का मान सकते हैं। मान लीजिए कि AB केंद्रीय रेखा है जिसकी लंबाई 8 सेमी है। हम इसे इस प्रकार लिखते हैं: AB = 8 सेमी। यहाँ, पहली लहर को आधे वृत्त के रूप में खींचा गया है।

उत्तर:

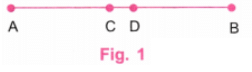
चरण 1: हम 8 सेमी लंबी केंद्रीय रेखा AB से शुरू करते हैं, मान लीजिए। (चित्र 1)

चरण 2: चूंकि 8 ÷ 2 = 4, शासक का उपयोग करते हुए, AB पर C बिंदु इस प्रकार लें कि AC = 4 सेमी। C, AB का मध्य बिंदु है। चूंकि 4 ÷ 2 = 2, शासक का उपयोग करते हुए, AC पर D और CB पर E बिंदु इस प्रकार लें कि AD = 2 सेमी और CE = 2 सेमी। D, AC का मध्य बिंदु है और E, CB का मध्य बिंदु है। (चित्र 2)

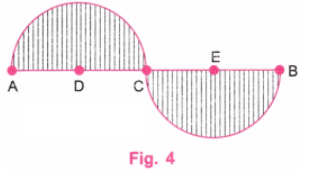
चरण 3: D के केंद्र पर, AB रेखा के ऊपर 2 सेमी त्रिज्या का एक अर्धवृत्त खींचें। E के केंद्र पर, AB रेखा के नीचे 2 सेमी त्रिज्या का एक अर्धवृत्त खींचें। (चित्र 3)

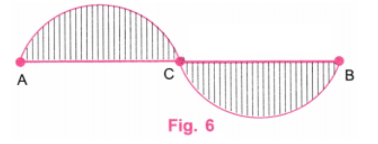
चरण 4: AB रेखा के ऊपर और नीचे अर्धवृत्तों में लंबवत रेखाएँ खींचें। (चित्र 4) चरण 5: चित्र 4 दी गई "लहराती लहर" का आवश्यक चित्रण प्रस्तुत करता है।

समझिए

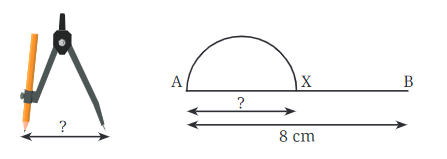
प्रश्न 1: इस अर्धवृत्त को प्राप्त करने के लिए कंपास में कौन सा त्रिज्या लिया जाना चाहिए? AX की लंबाई क्या होनी चाहिए? उत्तर: हमारे पास AB = 8 सेमी है। चूंकि "लहराती लहर" में दो समान अर्धवृत्त हैं, हमारे पास AX = XB है। ∴ X AB का मध्य बिंदु है। ∴ AX = 8/2 = 4 सेमी ∴ AX की लंबाई 4 सेमी है। मान लीजिए M AX का मध्य बिंदु है। ∴ AM = MX = 8/2 = 2 सेमी अर्धवृत्त का केंद्र M है। ∴ अर्धवृत्त की त्रिज्या = AM = 2 सेमी ∴ अर्धवृत्त की त्रिज्या 2 सेमी है।

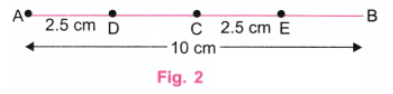
प्रश्न 2: एक अलग लंबाई की केंद्रीय रेखा लें और उस पर लहर खींचने का प्रयास करें। उत्तर: चरण 1: हम अलग-अलग लंबाई की केंद्रीय रेखा से शुरू करते हैं, मान लीजिए, 10 सेमी। (चित्र 1)

चरण 2: चूंकि 10/2 = 5, एक स्केल का उपयोग करके, AB पर बिंदु C लें ताकि AC = 5 सेमी हो। C AB का मध्य बिंदु है। चूंकि 5 ÷ 2 = 2.5, एक स्केल का उपयोग करके, AC पर D बिंदु और CB पर E बिंदु लें ताकि AD = 2.5 सेमी और CE = 2.5 सेमी हो। D AC का मध्य बिंदु है और E CB का मध्य बिंदु है। (चित्र 2)

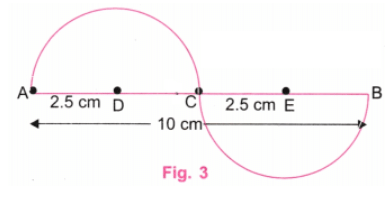
चरण 3: D पर केंद्र बनाकर AB केंद्रीय रेखा के ऊपर 2.5 सेमी की त्रिज्या वाला एक अर्धवृत्त खींचें। E पर केंद्र बनाकर AB केंद्रीय रेखा के नीचे 2.5 सेमी की त्रिज्या वाला एक अर्धवृत्त खींचें। (चित्र 3)

चरण 4: AB रेखा के ऊपर और नीचे अर्धवृत्तों में लंबवत रेखाएँ खींचें। (चित्र 4)

चरण 5: यह चित्र दी गई "लहराती लहर" का आवश्यक चित्रण प्रस्तुत करता है, जिसमें केंद्रीय रेखा की लंबाई 10 सेमी है।

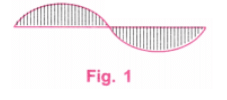
प्रश्न 3: उस चित्र को फिर से बनाने का प्रयास करें जहाँ लहरें अर्धवृत्त से छोटी हैं (जैसा कि चित्र 'एक व्यक्ति' के गर्दन में दिखता है)। यहाँ चुनौती यह है कि दोनों लहरें समान होनी चाहिए। यह कठिन हो सकता है! उत्तर: हम चित्र 1 में दिए गए रूप में "लहराती लहर" बनाएंगे।

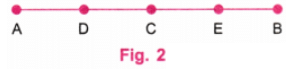
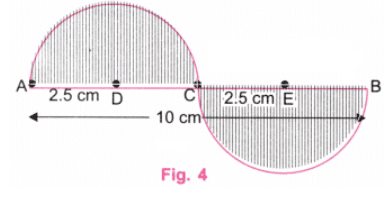
यहां, लहरें आधे वृत्त से छोटी हैं। चरण 1: हम 10 सेंटीमीटर लंबी केंद्रीय रेखा AB से शुरू करते हैं। (चित्र 2)

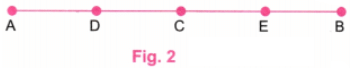
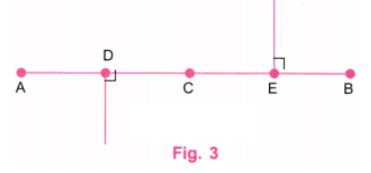
चरण 2: चूंकि 10 ÷ 2 = 5, एक पैमाने का उपयोग करते हुए AB पर एक बिंदु C लें, ताकि AC = 5 सेंटीमीटर हो। C, AB का मध्य बिंदु है। चूंकि 5 ÷ 2 = 2.5, एक पैमाने का उपयोग करते हुए, AC पर D और CB पर E बिंदुओं को ऐसे लें कि AD = 2.5 सेंटीमीटर और CE = 2.5 सेंटीमीटर हो। D, AC का मध्य बिंदु है और E, CB का मध्य बिंदु है। (चित्र 2) चरण 3: D पर, AB के नीचे एक लंबवत रेखा खींचें, एक प्रोट्रैक्टर का उपयोग करते हुए। E पर, AB के ऊपर एक लंबवत रेखा खींचें, एक प्रोट्रैक्टर का उपयोग करते हुए। (चित्र 3)

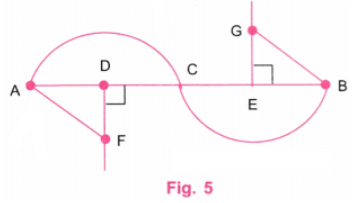
चरण 4: एक पैमाने का उपयोग करते हुए, बिंदुओं F और G को इस प्रकार चिह्नित करें कि DF = 1.5 सेंटीमीटर और EG = 1.5 सेंटीमीटर हो। DF और EG के बीच की समान दूरी भी 1.5 सेंटीमीटर से थोड़ी कम या अधिक हो सकती है। (चित्र 4) चरण 5: AF और BG को जोड़ें। F पर केंद्र रखते हुए, A से C तक एक आर्क खींचें जिसकी त्रिज्या AF के बराबर हो। G पर केंद्र रखते हुए, B से C तक एक आर्क खींचें जिसकी त्रिज्या GB के बराबर हो। (चित्र 5) चरण 6: चित्र 5 में लंबवत रेखाएं खींचें। साथ ही, चित्र 5 में अतिरिक्त रेखाएं मिटा दें जैसा कि चित्र 6 में दिखाया गया है। चरण 7: चित्र 6 एक "लहरदार लहर" का आवश्यक चित्रण प्रस्तुत करता है, जहां लहरें आधे वृत्त से छोटी हैं।

पृष्ठ 192

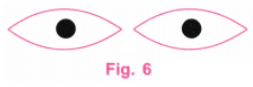
प्रश्न 3: आंखें इन आंखों को कंपास से कैसे खींचते हैं? उत्तर: चरण 1: 8.5 सेंटीमीटर (4 सेंटीमीटर 0.5 सेंटीमीटर 4 सेंटीमीटर) लंबी रेखा AB लें। AB पर बिंदु C और D लें ताकि AC = 4 सेंटीमीटर और AD = 4.5 सेंटीमीटर (4 सेंटीमीटर 0.5 सेंटीमीटर) हो। (चित्र 1) चरण 2: AB पर बिंदु E और F को इस प्रकार लें कि AE = 2 सेंटीमीटर और FB = 2 सेंटीमीटर हो। E, AC का मध्य बिंदु है और F, DB का मध्य बिंदु है। (चित्र 2) चरण 3: एक प्रोट्रैक्टर का उपयोग करते हुए, E और F पर लंबवत रेखाएं खींचें। (चित्र 3)

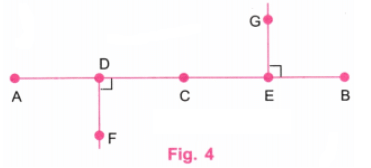
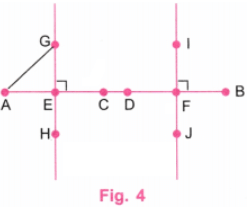
चरण 4: एक पैमाने का उपयोग करके, बिंदुओं G, H, I, और J को इस प्रकार लें कि EG, EH, FI, और FJ सभी 1.5 सेमी के बराबर हों। समान दूरी थोड़ी कम या अधिक भी हो सकती है (चित्र 4)

चरण 5: G पर केंद्र रखते हुए, A से C तक AG के बराबर त्रिज्या से एक आर्क खींचें। इसी तरह, H, I, और J पर केंद्र रखते हुए AG के बराबर त्रिज्या से आर्क खींचें। चित्र 5 में दिखाए अनुसार अतिरिक्त रेखाओं को मिटा दें।

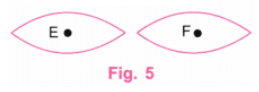
चरण 6: बिंदुओं E और F पर बड़े आकार के दो काले बिंदु बनाएं। (चित्र 6)

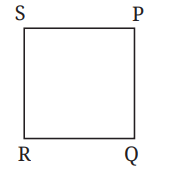
प्रश्न: निम्नलिखित में से कौन सा इस वर्ग का नाम नहीं है? 1. PQSR 2. SPQR 3. RSPQ 4. QRSP

पृष्ठ 194

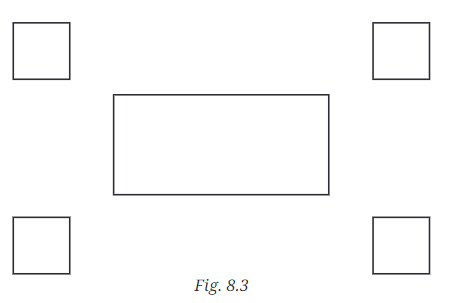
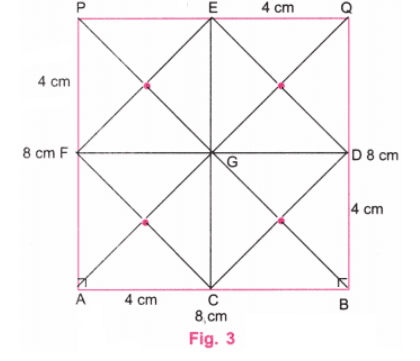
प्रश्न 1: दिए गए चित्र के अनुसार एक आयत और चार वर्गों का एक विन्यास बनाएं। चार वर्गों को आयत के चारों ओर सममित रूप से रखने के लिए आपने क्या किया? अपने सहपाठियों के साथ चर्चा करें।

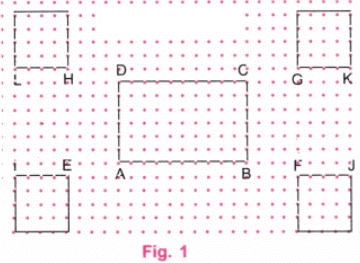
उत्तर: चरण 1: एक वर्ग डॉट कागज़ लें और उस पर A पर एक बिंदु चिह्नित करें। A से शुरू करते हुए, दाईं ओर 10 डॉट्स की दूरी पर जाएं और दसवें डॉट को B पर चिह्नित करें।

चरण 2: B से शुरू करते हुए, B के ऊपर 6 डॉट्स की दूरी पर जाएं और 6 वें डॉट को C के रूप में चिह्नित करें। A से शुरू करते हुए, A के ऊपर 6 डॉट्स की दूरी पर जाएं और 6 वें डॉट को D के रूप में चिह्नित करें। AB, BC, CD, और DA को जोड़ें।

चरण 3: चित्र में दिखाए अनुसार डॉट कागज़ पर E, F, G, और H बिंदुओं को लें।

चरण 4: E, F, G, और H से क्रमशः 4 डॉट्स की दूरी पर I, J, K, और L बिंदुओं को लें। IE, FJ, GK, और LH को जोड़ें।

चरण 5: LH और GK पर, आयत के ऊपर वर्ग बनाएं।

चरण 6: IE और FJ पर, आयत के नीचे वर्ग बनाएं।

चरण 7: यह चित्र एक आयत और चार वर्गों का आवश्यक विन्यास है जो वर्ग डॉट कागज़ पर है।

प्रश्न 2: इस संग्रह में क्या कोई वर्ग हैं? यदि आवश्यक हो, तो माप का उपयोग करें। विचार करें: क्या यह संभव है कि बिना किसी मापने वाले उपकरण का उपयोग किए यह तर्क किया जा सके कि किनारों की लंबाई समान है या नहीं, और कोण सीधे हैं या नहीं, केवल डॉट ग्रिड में कोनों की स्थिति को देखकर? उत्तर:

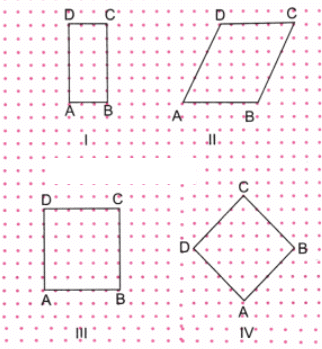
चित्र I: इस चित्र में, AB और BC समान नहीं हैं। इसलिए, ABCD एक वर्ग नहीं हो सकता। चित्र II: इस चित्र में, ∠BAD 90° के बराबर नहीं है। इसलिए, ABCD एक वर्ग नहीं हो सकता। चित्र III: इस चित्र में, किनारों के बीच बिंदुओं की गिनती करते समय, हमें पता चलता है कि AB, BC, CD और DA सभी समान लंबाई के हैं। साथ ही, किनारों पर बिंदुओं की स्थिति दिखाती है कि ABCD का प्रत्येक कोण 90° है। ∴ ABCD एक वर्ग है। चित्र IV: इस चित्र में, किनारों के बीच बिंदुओं की गिनती करते समय, हमें पता चलता है कि AB, BC, CD और DA सभी समान लंबाई के हैं। साथ ही, एक प्रोट्रैक्टर का उपयोग करते हुए, हम पाते हैं कि ABCD का प्रत्येक कोण 90° है। ∴ ABCD एक वर्ग है।

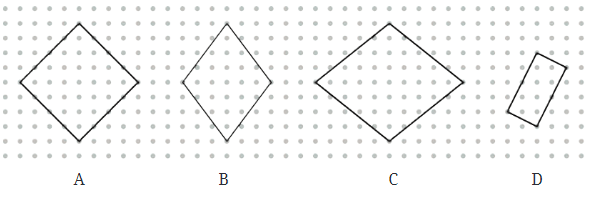
प्रश्न 3: डॉट ग्रिड पर कम से कम 3 घुमाए गए वर्ग और आयत खींचें। उन्हें इस तरह से खींचें कि उनके कोने बिंदुओं पर हों। जांचें कि आपने जो वर्ग और आयत खींचे हैं, वे अपनी-अपनी विशेषताओं को पूरा करते हैं। उत्तर: हमने डॉट ग्रिड पर दो घुमाए गए वर्ग (II और III) और दो घुमाए गए आयत (I और IV) खींचे हैं, ताकि वर्गों और आयतों के कोने बिंदुओं पर हों।

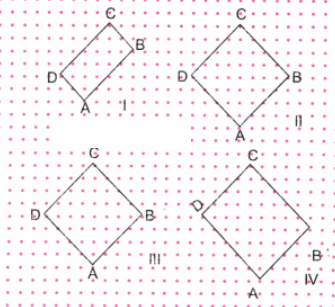
हमने दो घुमाए गए वर्ग (II और III) और दो घुमाए गए आयत (I और IV) खींचे हैं। ये वर्ग और आयत किनारों के बीच बिंदुओं की संख्या और किनारों की स्थिति को ध्यान में रखकर खींचे गए हैं। एक प्रोट्रैक्टर का उपयोग करते हुए, हम पाते हैं कि चित्र I से IV के सभी कोण 90° हैं। एक रूलर का उपयोग करते हुए, हम पाते हैं कि चित्र I और IV के विपरीत किनारे समान हैं और चित्र II और III के सभी किनारे समान हैं। ∴ परिभाषा के अनुसार, चित्र I और IV आयत हैं, और चित्र II और III वर्ग हैं।

पृष्ठ 197

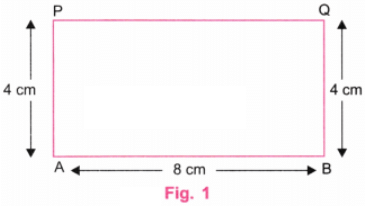
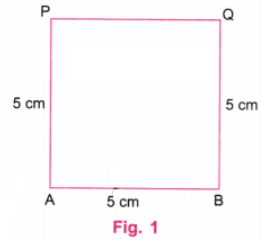
प्रश्न 1: 4 सेमी और 6 सेमी लम्बाई के किनारे वाले एक आयत को बनाएं। बनाने के बाद, जाँच करें कि क्या यह आयत के गुणों को पूरा करता है। उत्तर: हम चित्र 1 में दिखाए गए रूप में एक आयत बनाएंगे।

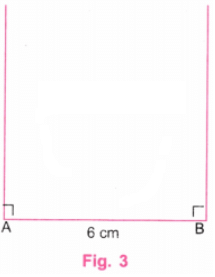
चरण 1: एक स्केल का उपयोग करके, AB रेखा को 6 सेमी लंबी बनाएं। (चित्र 2)

चरण 2: एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएँ खींचें। (चित्र 3)

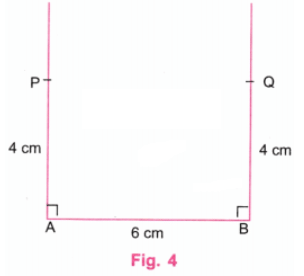
चरण 3: एक स्केल का उपयोग करके, A पर लंबवत रेखा पर P बिंदु को इस प्रकार चिह्नित करें कि AP = 4 सेमी। एक स्केल का उपयोग करके, B पर लंबवत रेखा पर Q बिंदु को इस प्रकार चिह्नित करें कि BQ = 4 सेमी। (चित्र 4)

चरण 4: स्केल का उपयोग करके P और Q को जोड़ें। P और Q के ऊपर की रेखाएँ मिटा दें। (चित्र 5)

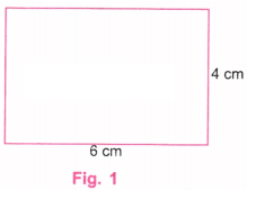
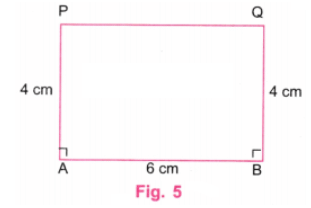
चरण 5: स्केल का उपयोग करके, जाँच करें कि PQ की लंबाई 6 सेमी है। प्रोट्रैक्टर का उपयोग करके, जाँच करें कि ∠P और ∠Q दोनों 90° हैं।

चरण 6: हमारे पास है:

• (i) AB = PQ = 6 सेमी और AP = BQ = 4 सेमी
• (ii) ∠A = ∠B = ∠Q = ∠P = 90°।

चरण 7: चित्र 5 में ABQP आवश्यक आयत है, जिसकी लंबाई 4 सेमी और 6 सेमी है।

प्रश्न 2: 2 सेमी और 10 सेमी लम्बाई के किनारे वाले एक आयत को बनाएं। बनाने के बाद, जाँच करें कि क्या यह आयत के गुणों को पूरा करता है। उत्तर: हम चित्र 1 में दिखाए गए रूप में एक आयत बनाएंगे।

चरण 1: एक स्केल का उपयोग करके, AB रेखा को 10 सेमी लंबी बनाएं। (चित्र 2)।

चरण 2: एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएँ खींचें। (चित्र 3)।

चरण 3: एक स्केल का उपयोग करके, A पर लंबवत रेखा पर P बिंदु को इस प्रकार चिह्नित करें कि AP = 2 सेमी। एक स्केल का उपयोग करके, B पर लंबवत रेखा पर Q बिंदु को इस प्रकार चिह्नित करें कि BQ = 2 सेमी। (चित्र 4)

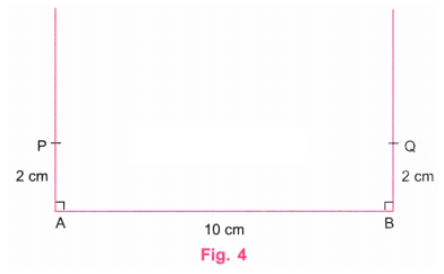
चरण 4: स्केल का उपयोग करके P और Q को जोड़ें। P और Q के ऊपर की रेखाएँ मिटा दें। (चित्र 5)

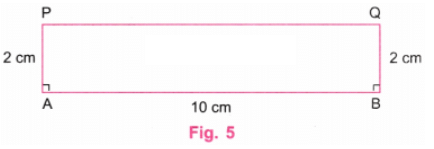
चरण 5: स्केल का उपयोग करके, जाँच करें कि PQ की लंबाई 10 सेमी है। प्रोट्रैक्टर का उपयोग करके, जाँच करें कि ∠P और ∠Q दोनों 90° हैं।

चरण 6: हमारे पास है:

• (i) AB = PQ = 10 सेमी और AP = BQ = 2 सेमी
• (ii) ∠A = ∠B = ∠P = ∠Q = 90°।

चरण 7: चित्र 5 में ABQP आवश्यक आयत है, जिसकी लंबाई 2 सेमी और 10 सेमी है।

प्रश्न 3: क्या 4-कोने वाली आकृति बनाना संभव है जिसमें-

• सभी कोण 90° हैं, लेकिन विपरीत भुजाएँ समान नहीं हैं?

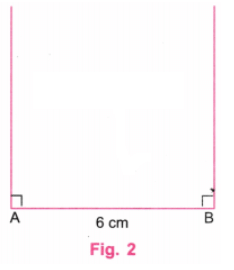
उत्तर: चरण 1: एक पैमाने का उपयोग करके, 6 सेंटीमीटर लंबाई की रेखा AB खींचें, मान लीजिए। (चित्र 1).

चरण 2: एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएँ खींचें (चित्र 2)।

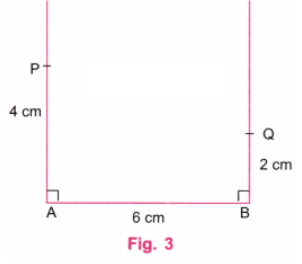
चरण 3: एक पैमाने का उपयोग करके, A पर लंबवत रेखा पर बिंदु P को इस प्रकार चिन्हित करें कि AP = 4 सेंटीमीटर। एक पैमाने का उपयोग करके, B पर लंबवत रेखा पर बिंदु Q को इस प्रकार चिन्हित करें कि BQ = 2 सेंटीमीटर, जो AP के बराबर नहीं है। (चित्र 3).

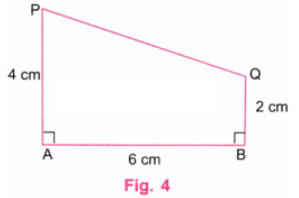
चरण 4: चित्र 3 में, AP और BQ की विपरीत भुजाएँ समान नहीं हैं। P और Q को एक पैमाने का उपयोग करके जोड़ें। P और Q के ऊपर की रेखाएँ मिटा दें (चित्र 4)।

चरण 5: एक प्रोट्रैक्टर का उपयोग करके, हम पाते हैं कि न तो ∠P और न ही ∠Q 90° हैं।

चरण 6: हम निष्कर्ष निकालते हैं कि ऐसा चार भुजाओं वाला आकृति बनाना संभव नहीं है जिसमें सभी कोण 90° हों और विपरीत भुजाएँ समान न हों।

पृष्ठ 199

प्रश्न: आयत को तोड़ना तीन समान वर्गों में विभाजित किया जा सकने वाला एक आयत बनाएं।

उत्तर: हम चित्र 1 में दिखाए गए रूप में एक आयत खींचेंगे।

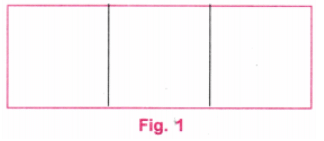
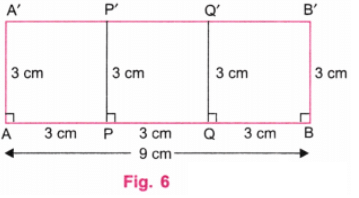
चरण 1: हम आयत की ऊर्ध्वाधर भुजा 3 सेंटीमीटर रखेंगे। चूंकि आयत को तीन समान वर्गों में विभाजित किया जाना है, आयत की लंबाई 3 सेंटीमीटर + 3 सेंटीमीटर + 3 सेंटीमीटर = 9 सेंटीमीटर होनी चाहिए।

चरण 2: एक पैमाने का उपयोग करके, 9 सेंटीमीटर लंबी रेखा AB खींचें। (चित्र 2).

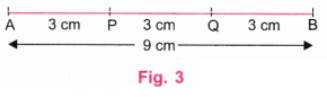
चरण 3: एक पैमाने का उपयोग करके, AB पर बिंदु P और Q को इस प्रकार खोजें कि AP = 3 सेंटीमीटर और PQ = 3 सेंटीमीटर। यहाँ, QB भी 3 सेंटीमीटर है। (चित्र 3).

चरण 4: एक प्रोट्रैक्टर का उपयोग करके, A, P, Q, और B पर लंबवत रेखाएँ खींचें। (चित्र 4).

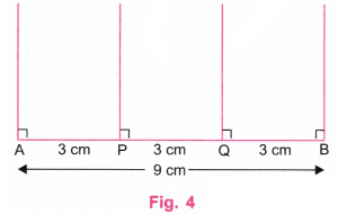
चरण 5: एक पैमाने का उपयोग करके, A, P, Q, और B पर लंबवत रेखाओं पर बिंदु A’, P’, Q’, और B’ को इस प्रकार चिन्हित करें कि AA’ = PP’ = QQ’ = BR’ = 3 सेंटीमीटर। (चित्र 5).

चरण 6: A’ और P’, P’ और Q’, और Q’ और B’ को एक पैमाने का उपयोग करके जोड़ें। A’, P’, Q’, और B’ के ऊपर की रेखाएँ मिटा दें। (चित्र 6).

चरण 7: ABB’A’ आवश्यक आयत है जो 3 समान वर्गों APP’A’, PQQ’P’, और QBB’Q’ में विभाजित है।

पृष्ठ 201

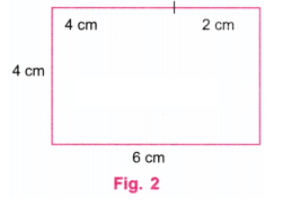
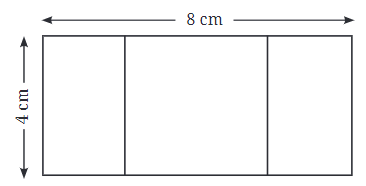
प्रश्न: एक आयत के किनारों की लंबाई बताएं जिसे निम्नलिखित में विभाजित नहीं किया जा सकता: (i) दो समान वर्गों में; (ii) तीन समान वर्गों में। उत्तर: (i) मान लें कि आयत का छोटा किनारा x सेमी है। यदि आयत का बड़ा किनारा 2x सेमी (x सेमी x सेमी) है, तो यह आयत दो समान वर्गों में विभाजित की जा सकती है जिनका किनारा x सेमी है। (चित्र 1) मान लेते हैं कि आयत के किनारे 4 सेमी और 6 सेमी हैं। यहाँ, 6, 8 (4 + 4) के बराबर नहीं है, इसलिए इसे दो समान वर्गों में विभाजित नहीं किया जा सकता जैसा कि चित्र 2 में दिखाया गया है।

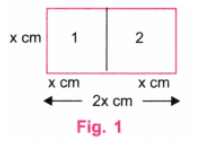
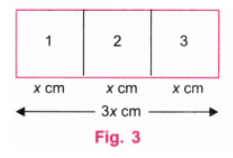
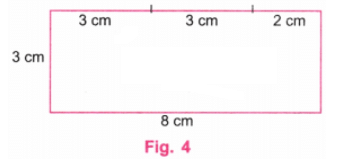
(ii) मान लें कि आयत का छोटा किनारा x सेमी है। यदि आयत का बड़ा किनारा 3x सेमी (x सेमी x सेमी x सेमी) है, तो यह आयत तीन समान वर्गों में विभाजित की जा सकती है जिनका किनारा x सेमी है। (चित्र 3) मान लेते हैं कि आयत के किनारे 3 सेमी और 8 सेमी हैं। यहाँ, 8, 9 (3 + 3 + 3) के बराबर नहीं है, इसलिए इसे तीन समान वर्गों में विभाजित नहीं किया जा सकता जैसा कि चित्र 4 में दिखाया गया है।

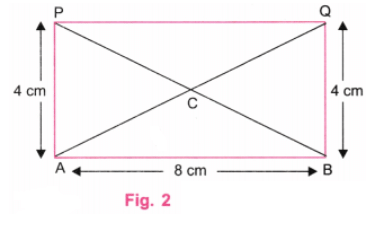
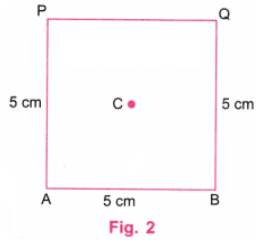
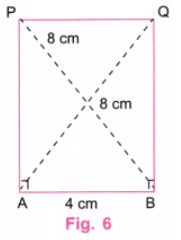
प्रश्न 1: एक आयत के भीतर एक वर्ग आयत के किनारों को 8 सेमी और 4 सेमी के साथ निर्माण करें। आप चित्र में दिखाए अनुसार, आयत के केंद्र के समान वर्ग का निर्माण कैसे करेंगे? सुझाव: एक मोटा चित्र बनाएं। वर्ग की किनारों की लंबाई क्या होगी? वर्ग के कोनों और बाहरी आयत के बीच की दूरी क्या होगी? उत्तर: एक आयत (या वर्ग) का केंद्र उसके विकर्णों के मिलन बिंदु है। चरण 1: एक पैमाना का उपयोग करके, 8 सेमी के बराबर एक रेखा AB खींचें। एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएं खींचें। एक पैमाना का उपयोग करके, A पर लंबवत रेखा पर बिंदु P को इस प्रकार चिह्नित करें कि AP = 4 सेमी। एक पैमाना का उपयोग करके, B पर लंबवत रेखा पर बिंदु Q को इस प्रकार चिह्नित करें कि BQ = 4 सेमी। P और Q को एक पैमाना का उपयोग करके जोड़ें। P और Q के ऊपर की रेखाओं को मिटा दें। (चित्र 1)

चरण 2: AQ और BP विकर्ण खींचें, एक पैमाना का उपयोग करके। मान लें कि विकर्ण C पर मिलते हैं। यह बिंदु आयत ABQP और आवश्यक वर्ग का केंद्र है। (चित्र 2)

चरण 3: विकर्ण AQ और BP को मिटा दें। एक प्रोट्रैक्टर का उपयोग करके, AB पर एक लंबवत रेखा खींचें और इसे केंद्र C के माध्यम से पार करें। मान लें कि यह लंबवत रेखा AB पर R और PQ पर S पर मिलती है। (चित्र 3).

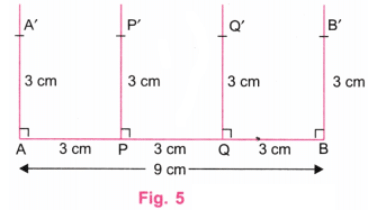
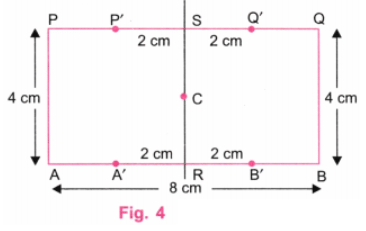
चरण 4: चूंकि AP = 4 सेमी है, प्रत्येक पक्ष का आकार 4 सेमी होना चाहिए। एक पैमाना का उपयोग करते हुए, AB पर A’ और B’ बिंदुओं को इस प्रकार चिह्नित करें कि A’R = 2 सेमी और RB’ = 2 सेमी हो। इस प्रकार, A’B’ = A’R + RB’ = 2 सेमी + 2 सेमी = 4 सेमी। इसी प्रकार, PQ पर P’ और Q’ बिंदुओं को इस प्रकार चिह्नित करें कि P’S = 2 सेमी और SQ’ = 2 सेमी हो। इस प्रकार, P’Q’ = P’S + SQ’ = 2 सेमी + 2 सेमी = 4 सेमी। (चित्र 4)।

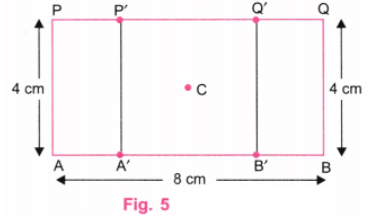
चरण 5: एक पैमाना का उपयोग करते हुए, A’ और P’ को जोड़ें और B’ और Q’ को भी जोड़ें। RS रेखा को मिटा दें। (चित्र 5)।

चरण 6: चित्र 5 में, A’B’Q’P’ आवश्यक वर्ग है जिसका केंद्र C है, जो दिए गए आयत का भी केंद्र है।

पृष्ठ 202

प्रश्न 2: गिरते वर्ग “Falling Squares” चित्र को नीचे दिखाए अनुसार बनाएँ:

सुनिश्चित करें कि वर्ग उसी तरह संरेखित हैं जैसे वे दिखाए गए हैं। अब, इसे आजमाएँ। उत्तर: दिए गए चित्र में, तीन गिरते वर्ग हैं और प्रत्येक वर्ग का आकार 4 सेमी है।

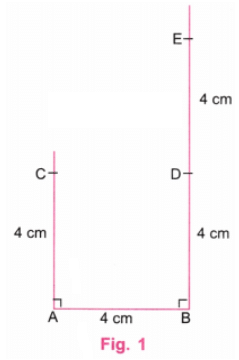
चरण 1: एक पैमाना का उपयोग करते हुए, 4 सेमी के बराबर रेखा AB खींचें। एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएँ खींचें। एक पैमाना का उपयोग करते हुए, A पर लंबवत रेखा पर बिंदु C को इस प्रकार चिह्नित करें कि AC = 4 सेमी। एक पैमाना का उपयोग करते हुए, B पर लंबवत रेखा पर बिंदु D और E को इस प्रकार चिह्नित करें कि BD = 4 सेमी और DE = 4 सेमी। (चित्र 1)।

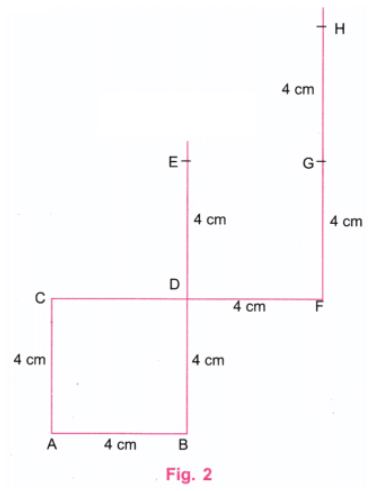
चरण 2: C और D को जोड़ें। CD को F तक बढ़ाएँ ताकि DF = 4 सेमी हो। एक प्रोट्रैक्टर का उपयोग करके, F पर एक लंबवत रेखा खींचें। एक पैमाना का उपयोग करते हुए, F पर लंबवत रेखा पर बिंदु G और H को इस प्रकार चिह्नित करें कि FG = 4 सेमी और GH = 4 सेमी। (चित्र 2)।

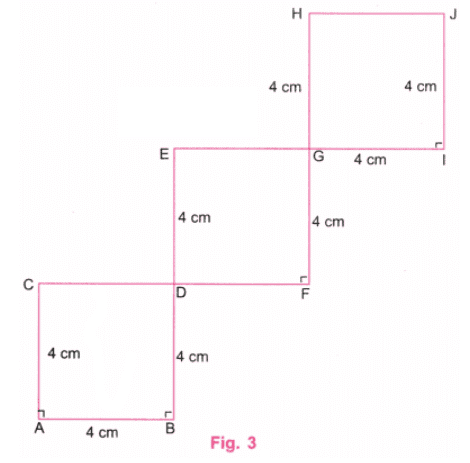
चरण 3: E और G को जोड़ें। EG को I तक बढ़ाएँ ताकि GE = 4 सेमी हो। एक प्रोट्रैक्टर का उपयोग करके, I पर एक लंबवत रेखा खींचें। एक पैमाना का उपयोग करते हुए, I पर लंबवत रेखा पर बिंदु J को इस प्रकार चिह्नित करें कि IJ = 4 सेमी हो। H और J को जोड़ें। चित्र में अतिरिक्त रेखाओं को मिटा दें। (चित्र 3)।

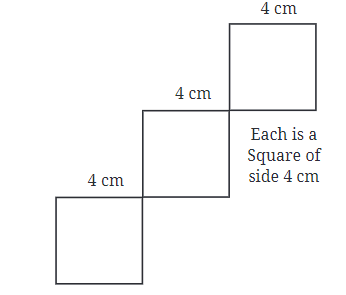
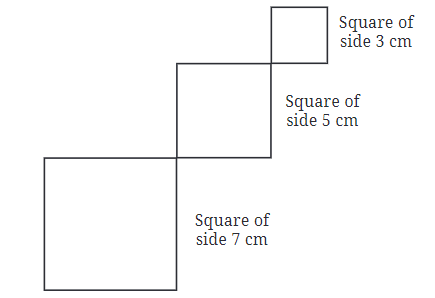
चरण 4: चित्र 3 में तीन “गिरते हुए वर्ग” हैं, प्रत्येक का आकार 4 सेमी है।

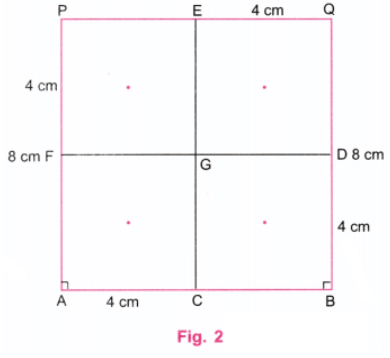
प्रश्न 3: शेडिंग: नीचे दिए गए चित्र का निर्माण करें। अपनी पसंद का मापन चुनें। ध्यान दें कि बड़ा 4-भुजाकार आकार वर्ग है और छोटे भी।

उत्तर:

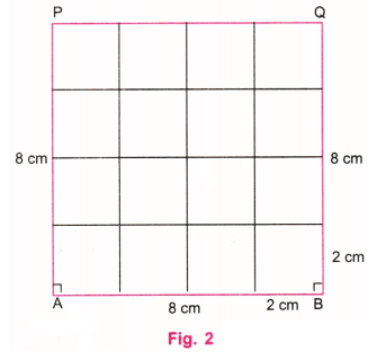
• चरण 1: एक रूलर का उपयोग करके, 8 सेमी लंबी AB रेखा खींचें। क्योंकि, 8 ÷ 4 = 2, हम 2 सेमी के छोटे वर्ग बनाएंगे। एक प्रोट्रैक्टर का उपयोग करके A और B पर लंबवत रेखाएँ खींचें। एक रूलर का उपयोग करके, लंबवत रेखा पर A पर P बिंदु को इस तरह चिह्नित करें कि AP = 8 सेमी। एक रूलर का उपयोग करके, लंबवत रेखा पर B पर Q बिंदु को इस तरह चिह्नित करें कि BQ = 8 सेमी। रूलर का उपयोग करके P और Q को जोड़ें। P और Q के ऊपर की रेखाएँ मिटा दें (चित्र 1)।
• चरण 2: AB, BQ, QP, और PA रेखाओं पर, रूलर का उपयोग करके, 2 सेमी की दूरी पर बिंदु चिह्नित करें। 16 वर्ग प्राप्त करने के लिए क्षैतिज और ऊर्ध्वाधर रेखाएँ खींचें। (चित्र 2)

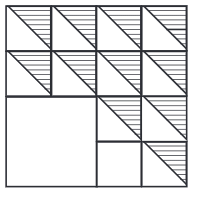
चरण 3: कोने A से, चार वर्गों के आंतरिक पक्षों को मिटाकर 4 सेमी का एक वर्ग प्राप्त करें, जिसका एक कोना A पर है। प्रत्येक का आकार 2 सेमी के शेष 12 छोटे वर्गों के समानांतर तिर्यक रेखाएँ खींचें। (चित्र 3)

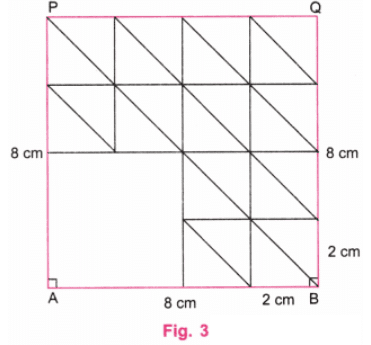
चरण 4: 12 छोटे वर्गों में, तिर्यक रेखाओं के ऊपर के भाग में क्षैतिज रेखाएँ खींचें। (चित्र 4)

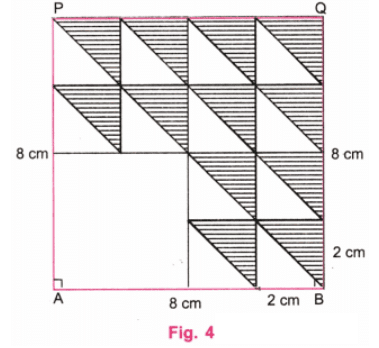
चरण 5: चित्र 4 आवश्यक चित्र है जिसमें एक वर्ग में 12 छोटे वर्ग हैं।

पृष्ठ 203

प्रश्न 4: एक छिद्र वाला वर्ग

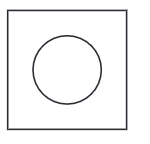
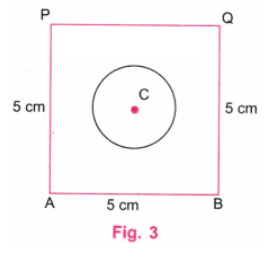
ध्यान दें कि गोल छिद्र वर्ग के केंद्र के समान है। दिए गए चित्र में “छिद्र वाला वर्ग” बनाएं। छिद्र का केंद्र वर्ग के केंद्र के समान है। संकेत: सोचें कि वृत्त का केंद्र कहाँ होना चाहिए।

उत्तर: एक वर्ग का केंद्र उसके तिर्यक रेखाओं के प्रतिच्छेदन का बिंदु होता है। यह केंद्र चित्र में छिद्र का भी केंद्र है।

• चरण 1: एक रूलर का उपयोग करके, 5 सेमी लंबी AB रेखा खींचें। एक प्रोट्रैक्टर का उपयोग करके A और B पर लंबवत रेखाएँ खींचें। एक रूलर का उपयोग करके, लंबवत रेखा पर A पर P बिंदु को इस तरह चिह्नित करें कि AP = 5 सेमी। एक रूलर का उपयोग करके, लंबवत रेखा पर B पर Q बिंदु को इस तरह चिह्नित करें कि BQ = 5 सेमी। रूलर का उपयोग करके P और Q को जोड़ें। P और Q के ऊपर की रेखाएँ मिटा दें (चित्र 1)।

चरण 2: एक शासक का उपयोग करते हुए AQ और BP परDiagonal खींचें। मान लीजिए कि ये diagonals C पर मिलती हैं। यह बिंदु वर्ग ABQP का केंद्र है। Diagonals AQ और BP को मिटा दें। (चित्र 2).

चरण 3: C पर केंद्र और 1.5 सेमी की त्रिज्या लेकर, एक कंपास का उपयोग करके एक वृत्त खींचें। (चित्र 3)

चरण 4: चित्र 3 आवश्यक “छिद्र वाला वर्ग” है।

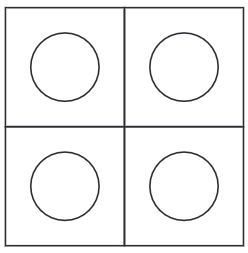
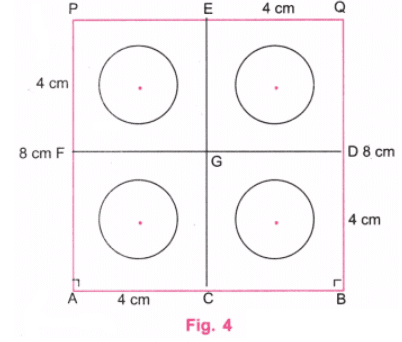
Q5: अधिक छिद्र वाले वर्ग “चार छिद्र वाला वर्ग” बनाएं जैसा कि दिए गए चित्र में दिखाया गया है। उत्तर: चित्र में, एक वृत्त का केंद्र वर्ग के केंद्र के समान है।

चरण 1: एक शासक का उपयोग करके, AB नाम की एक रेखा खींचें जो 8 सेमी लंबी हो। एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएँ खींचें। एक शासक का उपयोग करते हुए, A पर लंबवत रेखा पर बिंदु P को इस प्रकार चिह्नित करें कि AP = 8 सेमी। एक शासक का उपयोग करते हुए, B पर लंबवत रेखा पर बिंदु Q को इस प्रकार चिह्नित करें कि BQ = 8 सेमी। P और Q को एक शासक का उपयोग करके जोड़ें। P और Q के ऊपर की रेखाओं को मिटा दें। (चित्र 1)

चरण 2: एक शासक का उपयोग करके, बिंदु C, D, E, और F को इस प्रकार खोजें कि AC = 4 सेमी, BD = 4 सेमी, QE = 4 सेमी, और PF = 4 सेमी। C और E को जोड़ें और F और D को भी जोड़ें। (चित्र 2)

चरण 3: मान लीजिए कि G FD और CE रेखाओं का संगम है। ACGF, CBDG, DQEG, और GEPF वर्गों के केंद्रों को उनके संबंधित diagonals को जोड़कर खोजें। (चित्र 3)

चरण 4: छोटे वृत्तों के केंद्रों को खोजने के लिए उपयोग की गई अतिरिक्त रेखाओं को मिटा दें। छोटे वर्गों के केंद्रों पर केंद्र के साथ, 1.3 सेमी की त्रिज्या पर चार वृत्त बनाएं। (चित्र 4)

चरण 5: चित्र 4 आवश्यक “चार छिद्र वाला वर्ग” है।

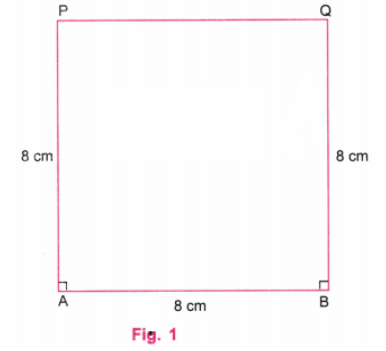
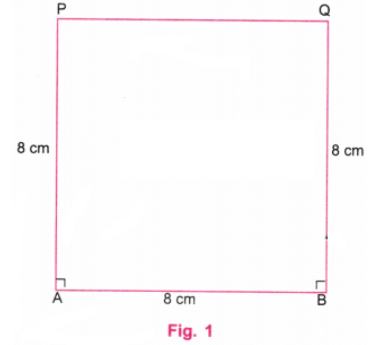
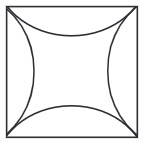
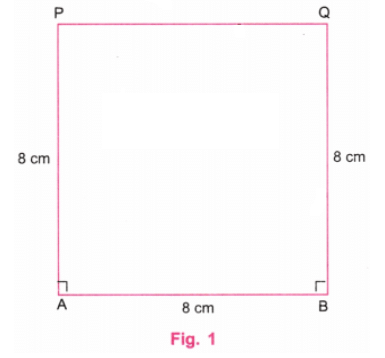
Q6: वक्रों वाला वर्ग यह एक 8 सेमी की भुजाओं वाला वर्ग है। “वक्रों वाला वर्ग” बनाएं, 8 सेमी की भुजा वाले वर्ग को दिए गए चित्र के रूप में लें। संकेत: सोचें कि कंपास की टिप को कहाँ रखा जा सकता है ताकि सभी 4 आर्च हर एक पक्ष से समान रूप से बाहर निकले। इसे आजमाएं!

उत्तर: दिए गए चित्र में, चार आर्च के केंद्र वर्ग के बाहर हैं।

चरण 1: एक शासक का उपयोग करते हुए, AB नाम की एक रेखा खींचें जो 8 सेमी लंबी हो। एक प्रोट्रैक्टर का उपयोग करके, A और B पर लंबवत रेखाएँ खींचें। एक शासक का उपयोग करते हुए, A पर लंबवत रेखा पर बिंदु P को इस प्रकार चिह्नित करें कि AP = 8 सेमी। एक शासक का उपयोग करते हुए, B पर लंबवत रेखा पर बिंदु Q को इस प्रकार चिह्नित करें कि BQ = 8 सेमी। P और Q को एक शासक का उपयोग करके जोड़ें। P और Q के ऊपर की रेखाओं को मिटा दें। (चित्र 1)

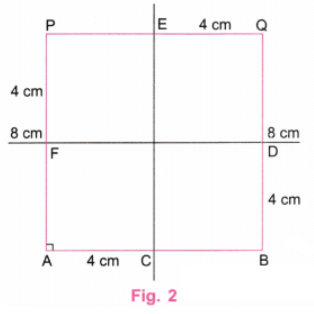
चरण 2: एक शासक का उपयोग करके, बिंदु C, D, E, और F को इस प्रकार चिह्नित करें कि AC = 4 सेमी, BD = 4 सेमी, QE = 4 सेमी, और PF = 4 सेमी। C और E को जोड़ें और D और F को भी जोड़ें। इन रेखाओं को वर्ग के बाहर बढ़ाएँ। (चित्र 2)

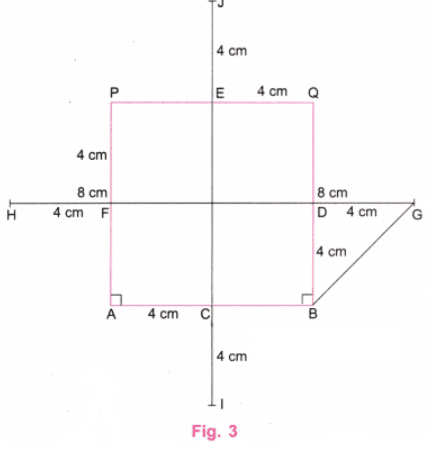
चरण 3: DF को बढ़ाएँ और उस पर बिंदु G और H लें ताकि DG और FH 4 सेमी के बराबर हों। CE को बढ़ाएँ और उस पर बिंदु I और J लें ताकि Cl और EJ 4 सेमी के बराबर हों। 4 सेमी की दूरी को थोड़ा कम या ज्यादा लिया जा सकता है। B और G को जोड़ें। (चित्र 3)

चरण 4: G, H, I, और J पर केंद्र के साथ और BG के बराबर त्रिज्या लेकर, दिए गए चित्र के अनुसार वर्ग के अंदर चार आर्च खींचें। अतिरिक्त रेखाओं को मिटा दें। (चित्र 4)

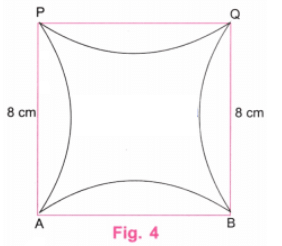
चरण 5: चित्र 4 आवश्यक “वक्रों वाला वर्ग” है, जिसकी भुजा 8 सेमी है।

पृष्ठ 204

प्रश्न 1: कोणों और भुजाओं के संबंध में आपने कौन से सामान्य नियम देखे? इन्हें अपने सहपाठियों के साथ चर्चा करें।

प्रश्न 2: आप कैसे सुनिश्चित कर सकते हैं कि आपने जो नियम देखे हैं, वे हमेशा सत्य होंगे?

पृष्ठ 208

प्रश्न 1: हम इसे कैसे पहचानते हैं? B के स्थान के बारे में हमें और क्या पता है? हमें पता है कि यह बिंदु D से 7 सेमी की दूरी पर है।

पृष्ठ 211

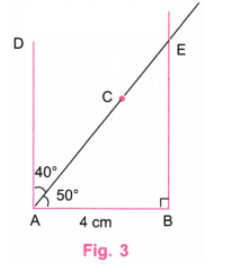
प्रश्न 1: एक आयत का निर्माण करें जिसमें एक विकर्ण विपरीत कोणों को 50° और 40° में विभाजित करता है। उत्तर: हम चित्र 1 के रूप में एक आयत बनाएंगे।

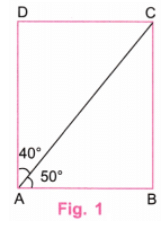
चरण 1: एक पैमाने का उपयोग करते हुए, एक रेखा AB खींचें जो 4 सेमी के बराबर हो। (चित्र 2)

चरण 2: एक प्रोट्रैक्टर का उपयोग करते हुए, कोण 50° और 90° (50° 40°) पर बिंदु C और D चिह्नित करें, प्रोट्रैक्टर के केंद्रीय बिंदु को A पर रखते हुए। (चित्र 3)

चरण 3: एक प्रोट्रैक्टर का उपयोग करते हुए, B पर AB के लंबवत रेखा खींचें और इसे विस्तारित रेखा AC पर E पर इंटरसेक्ट करें। (चित्र 3)

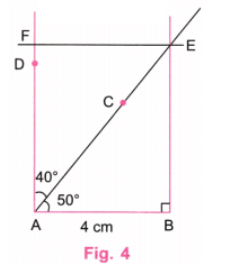
चरण 4: एक प्रोट्रैक्टर का उपयोग करते हुए, E पर BE के लंबवत रेखा खींचें और इसे विस्तारित रेखा AD पर F पर इंटरसेक्ट करें। (चित्र 4)

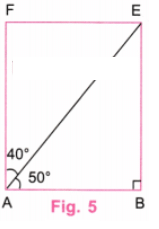
चरण 5: चित्र 4 में अतिरिक्त रेखाओं को मिटा दें। (चित्र 5)

चरण 6: चित्र 5 आवश्यक आयत है जिसमें एक विकर्ण विपरीत कोणों को 50° और 40° में विभाजित करता है।

प्रश्न 2: एक आयत का निर्माण करें जिसमें एक विकर्ण विपरीत कोणों को 45° और 45° में विभाजित करता है। आप भुजाओं के बारे में क्या अवलोकन करते हैं? उत्तर:

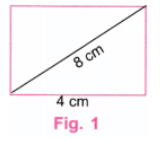
प्रश्न 3: एक आयत का निर्माण करें जिसमें एक भुजा 4 सेमी है और विकर्ण की लंबाई 8 सेमी है। उत्तर: हम चित्र 1 के रूप में एक आयत बनाएंगे।

चरण 1: एक पैमाने का उपयोग करते हुए, एक रेखा AB खींचें जो 4 सेमी के बराबर हो। (चित्र 2)

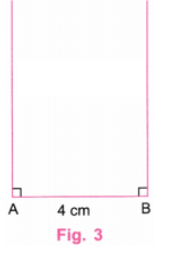
चरण 2: एक प्रोट्रैक्टर का उपयोग करते हुए, A और B पर AB के लंबवत रेखा खींचें। (चित्र 3)

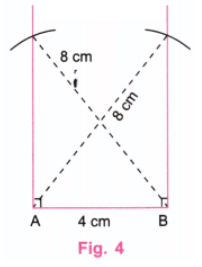
चरण 3: A पर केंद्र और 8 सेमी की त्रिज्या के साथ एक आर्क बनाएं जो लंबवत रेखा पर B से इंटरसेक्ट करे। इसी तरह, B पर केंद्र और 8 सेमी की त्रिज्या के साथ एक आर्क बनाएं जो लंबवत रेखा पर A से इंटरसेक्ट करे। (चित्र 4)

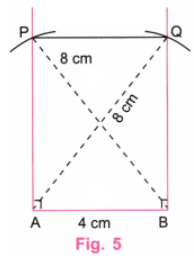
चरण 4: PQ के माध्यम से आर्क के इंटरसेक्शन बिंदुओं को जोड़ें। (चित्र 5)

चरण 5: चित्र 5 में अतिरिक्त रेखाओं को मिटा दें। (चित्र 6)

चरण 6: चित्र 6 आवश्यक आयत है जिसमें एक भुजा 4 सेमी और विकर्ण की लंबाई 8 सेमी है।

प्रश्न 4: एक आयत का निर्माण करें जिसमें एक भुजा 3 सेमी है और विकर्ण की लंबाई 7 सेमी है। उत्तर:

पृष्ठ 215

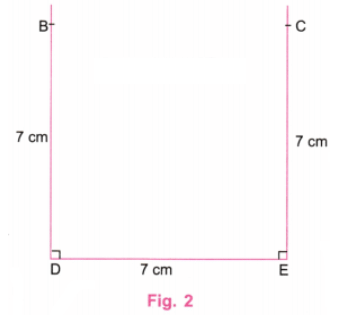
प्रश्न 1: एक बड़ा घर बनाएं, जिसमें सभी किनारों की लंबाई 7 सेमी हो। दिए गए चित्र को फिर से बनाएं। ध्यान दें कि घर के बॉर्डर को बनाने वाली सभी रेखाएँ 7 सेमी लंबी हैं। उत्तर:

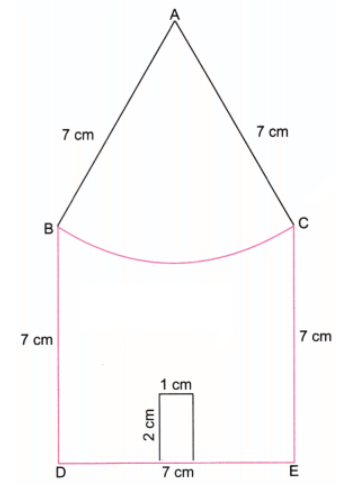
चरण 1: एक रूलर का उपयोग करते हुए, DE रेखा को 7 सेमी लंबा खींचें। (चित्र 1)

चरण 2: एक प्रोट्रैक्टर का उपयोग करते हुए, D और E पर DE के प्रति लंबवत रेखाएँ खींचें। B बिंदु को D पर इस तरह से लें कि BD = 7 सेमी हो। E पर लंबवत C बिंदु को इस तरह से लें कि CE = 7 सेमी हो। (चित्र 2)

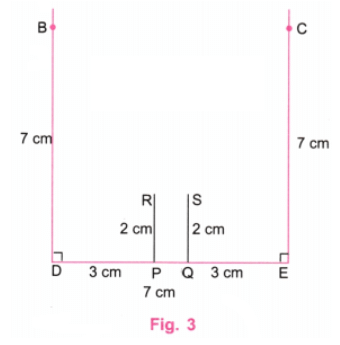
चरण 3: 7 सेमी – 1 सेमी = 6 सेमी और 6 सेमी ÷ 2 = 3 सेमी। एक रूलर का उपयोग करते हुए, DE पर P और Q बिंदुओं को इस तरह से लें कि DP = 3 सेमी और QE = 3 सेमी हो। एक प्रोट्रैक्टर का उपयोग करते हुए, P और Q पर DE के प्रति लंबवत 2 सेमी लंबी रेखाएँ खींचें। (चित्र 3)

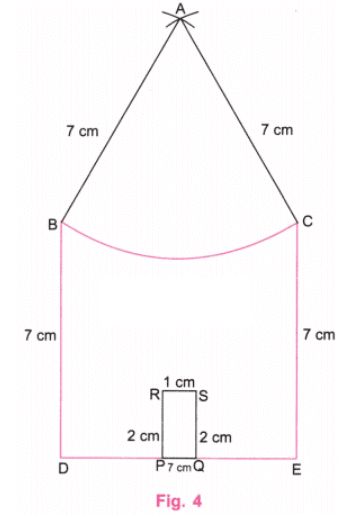
चरण 4: R और S को जोड़ें। B और C पर केंद्र रखते हुए और 7 सेमी की त्रिज्या के साथ, आकर्षण बनाएं जो A बिंदु पर मिलते हैं। AB और AC को जोड़ें। A पर केंद्र रखते हुए और 7 सेमी की त्रिज्या के साथ, B से C तक एक आर्क खींचें। साथ ही, अतिरिक्त रेखाओं को मिटा दें। (चित्र 4)

चरण 5: चित्र 4 दिए गए घर का आवश्यक पुनर्निर्माण है जिसमें सभी रेखाएँ 7 सेमी लंबी हैं।

प्रश्न 2: ‘एक व्यक्ति’, ‘लहराती लहर’, और ‘आँखें’ को ‘घर’ निर्माण में शामिल विचारों का उपयोग करके फिर से बनाने का प्रयास करें। उत्तर:

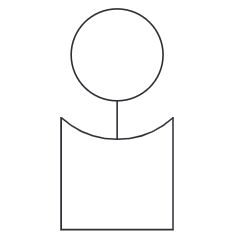
प्रश्न 3: क्या कोई 4-कोणीय आकृति है जिसमें सभी किनारे समान लंबाई के हैं लेकिन वर्ग नहीं हैं? यदि ऐसी आकृति है, तो क्या आप इसे बना सकते हैं? उत्तर:

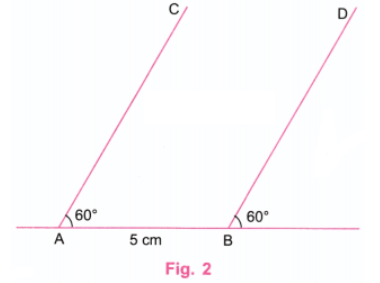
चरण 1: एक रेखा खींचें और उस पर A और B बिंदुओं को इस तरह से लें कि AB = 5 सेमी हो। (चित्र 1)

चरण 2: एक प्रोट्रैक्टर का उपयोग करते हुए, C और D बिंदुओं को इस तरह से लें कि A के दाईं ओर और B के दाईं ओर 60° कोण हों। (चित्र 2)

चरण 3: एक रूलर का उपयोग करते हुए, AC पर P बिंदु लें ताकि AC = 5 सेमी हो और BD पर Q बिंदु लें ताकि BD = 5 सेमी हो। P और Q को जोड़ें। (चित्र 3)

चरण 4: एक रूलर का उपयोग करते हुए, PQ की दूरी मापें। PQ 5 सेमी के बराबर है। इस प्रकार, आकृति ABQP में प्रत्येक किनारा 5 सेमी के बराबर है। यहाँ ∠A 60° है, जो 90° के बराबर नहीं है। इसलिए, ABQP एक वर्ग नहीं है।

चरण 5: हम पाते हैं कि ऐसे 4-कोणीय आकृतियाँ हैं जिनमें सभी किनारे समान लंबाई के हैं लेकिन वे वर्ग नहीं हैं।