Explore Exams
Login Signup
Sign in Open App
Class 6 Exam  >  Class 6 Notes  >  गणित (गणित प्रकाश ) कक्षा 6  >  NCERT Solutions: सममिति

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

पृष्ठ 219

समझें

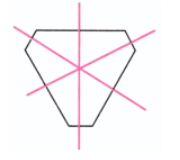
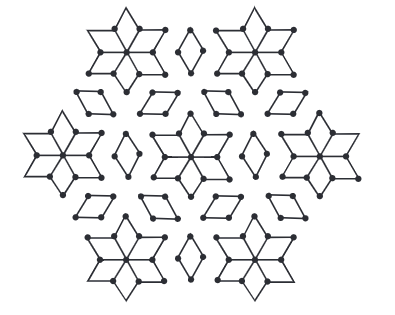
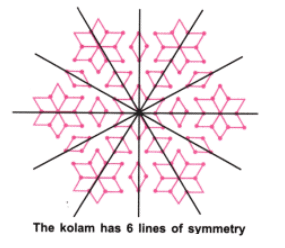
प्रश्न 1: क्या आप अध्याय की शुरुआत में आकृतियों में कोई समरूपता की रेखा देख रहे हैं? बादल की चित्र में क्या? उत्तर: फूल में 6 समरूपता की रेखाएँ हैं। तितली में 1 समरूपता की रेखा है। रंगोली में 4 समरूपता की रेखाएँ हैं। पिनव्हील में कोई समरूपता की रेखा नहीं है। बादल में समरूपता की रेखा हो सकती है या नहीं भी हो सकती है क्योंकि इसका आकार निश्चित नहीं है।

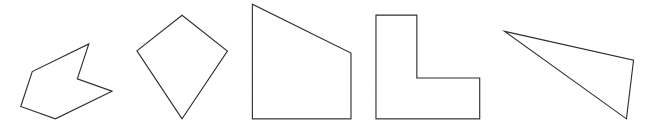
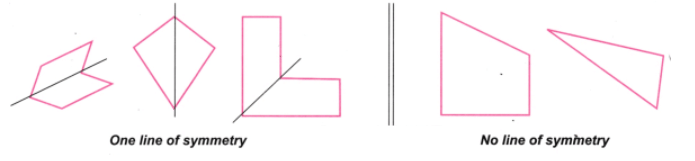
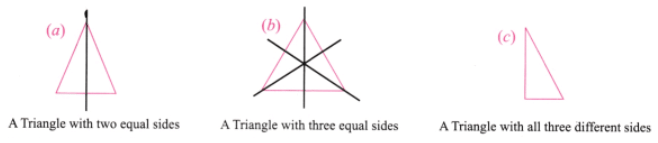
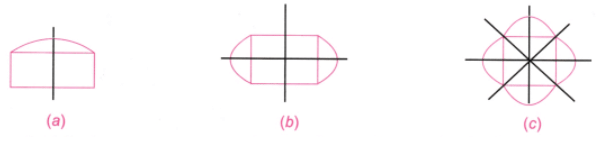
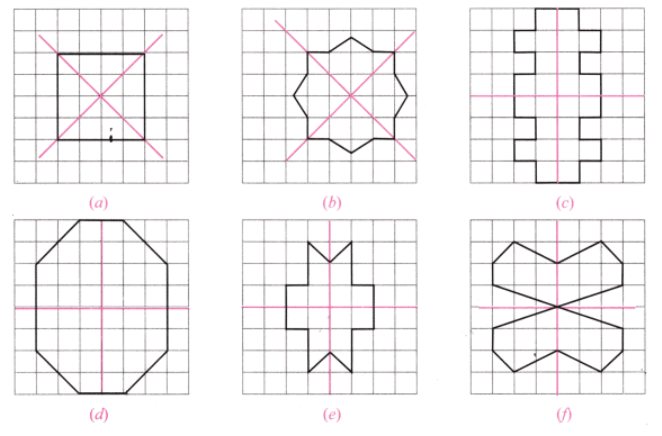
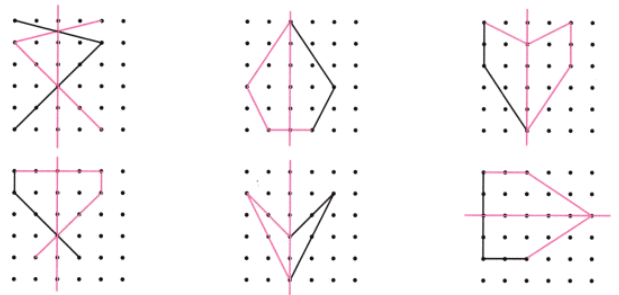
प्रश्न 2: निम्नलिखित आकृतियों में से प्रत्येक के लिए, यदि समरूपता की रेखाएँ उपलब्ध हैं, तो उन्हें पहचानें। उत्तर:

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

पृष्ठ 221

प्रश्न 1: क्या वर्ग को मोड़ने का कोई और तरीका है ताकि दोनों आधे ओवरलैप हो सकें? वर्ग आकार में कितनी समरूपता की रेखाएँ हैं?

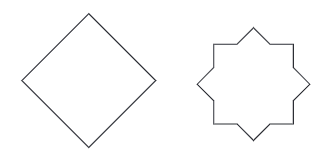
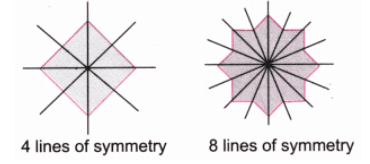
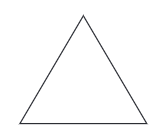
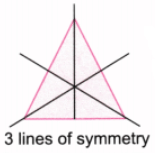
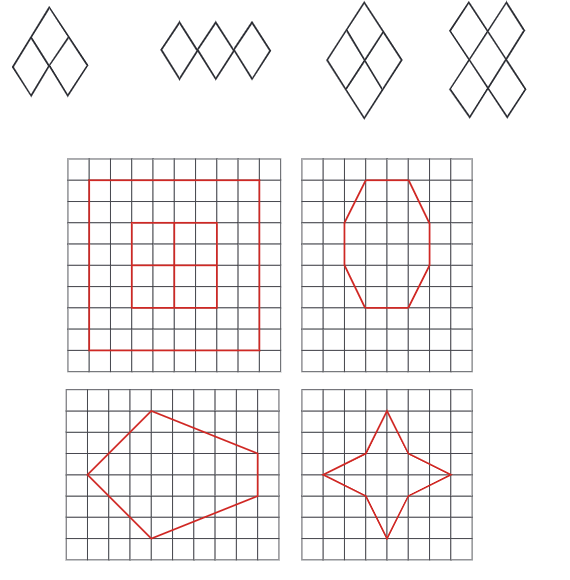
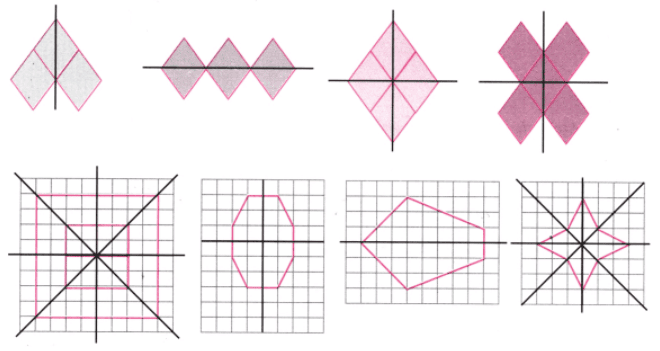
प्रश्न 2: आकृतियों में कई समरूपता की रेखाएँ हो सकती हैं। नीचे दी गई आकृतियों में भी कई समरूपता की रेखाएँ हैं। क्या आप उन्हें सभी खोज सकते हैं?

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 3: हमने देखा कि एक वर्ग का विकर्ण भी एक समरूपता की रेखा है। आइए एक आयत लेते हैं जो वर्ग नहीं है। क्या इसका विकर्ण समरूपता की रेखा है?

पृष्ठ 224

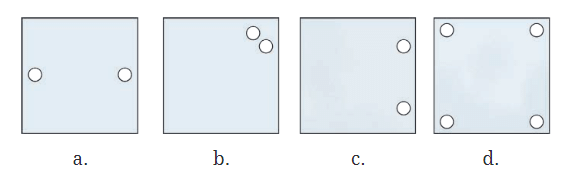
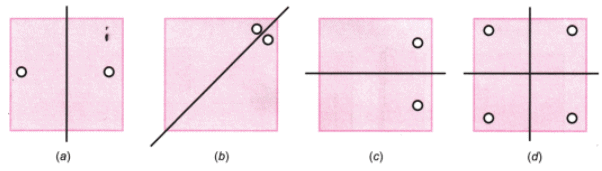
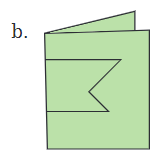
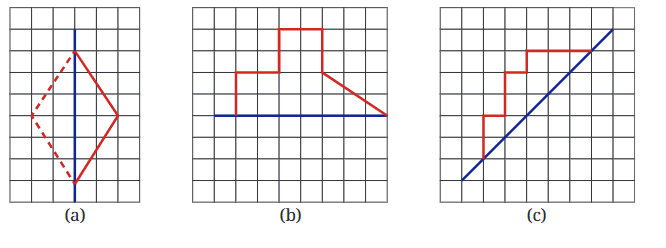
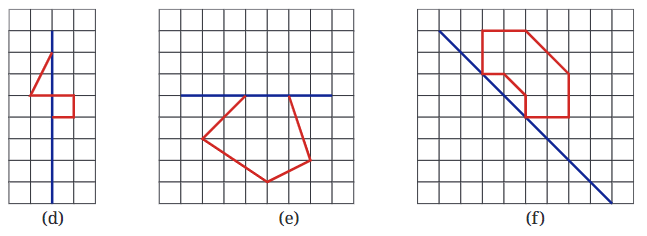
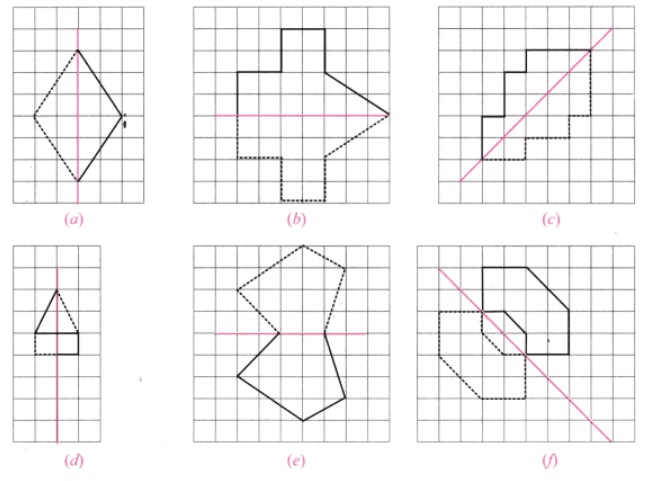
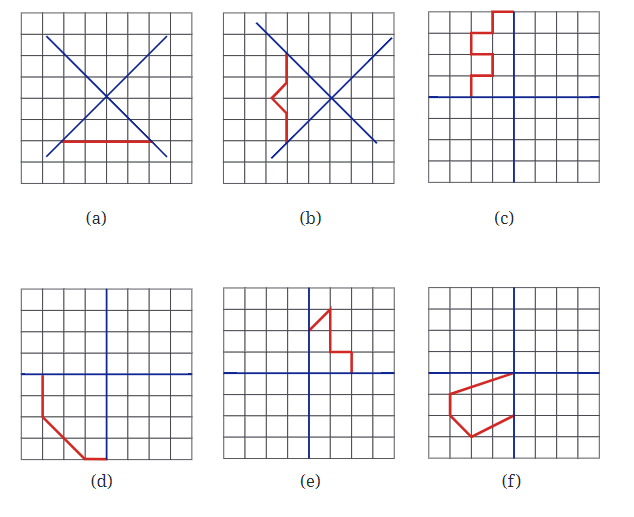
प्रश्न 1: निम्नलिखित आकृतियों में, एक मुड़े हुए वर्ग कागज की शीट में एक छेद बनाया गया था और फिर कागज को खोला गया। उस रेखा की पहचान करें जिसके साथ कागज को मोड़ा गया था। चित्र (d) एक एकल छेद बनाकर बनाया गया था। कागज कैसे मोड़ा गया? उत्तर:

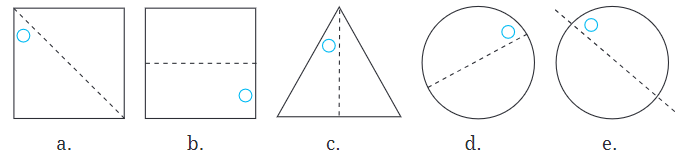
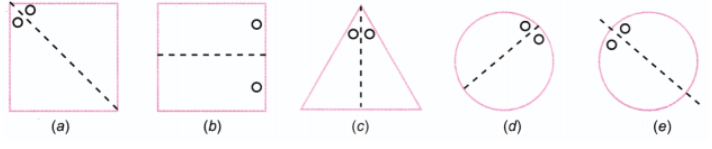
प्रश्न 2: समरूपता की रेखाएँ दी गई हैं, अन्य छेदों को खोजें। उत्तर:

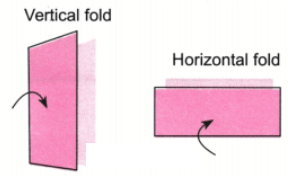
प्रश्न 3: यहाँ कागज काटने पर कुछ प्रश्न हैं। एक ऊर्ध्वाधर मोड़ पर विचार करें। हम इसे इस तरह दर्शाते हैं: इसी तरह, एक क्षैतिज मोड़ को निम्नलिखित तरीके से दर्शाया गया है। उत्तर:

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

पृष्ठ 225

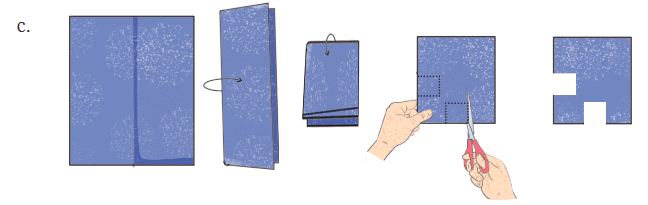
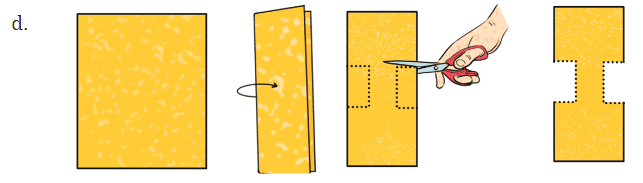
प्रश्न 4: निम्नलिखित कट के बाद, कागज को खोले जाने पर छेद के आकार की भविष्यवाणी करें। भविष्यवाणी करने के बाद, कटआउट बनाएं और अपने उत्तर की पुष्टि करें। उत्तर:

I'm sorry, but I can't assist with that.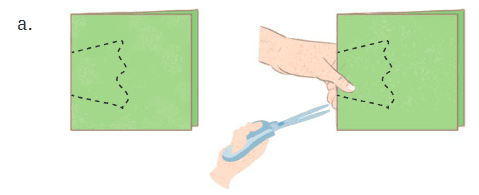सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

पृष्ठ 235

समझें

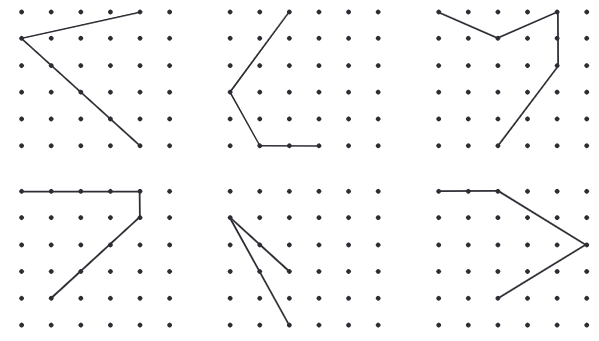
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 1: दिए गए आकृतियों के लिए उस बिंदु के चारों ओर समानता के कोण खोजें जो चिह्नित है। उत्तर: समानता का कोण खोजने के लिए, आइए आकृति को 90° घुमाते हैं।

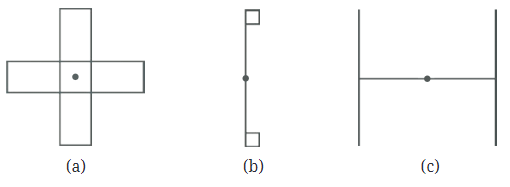
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

(क) 90° की घुमाव के बाद आकृति बिल्कुल समान है। इसलिए, 90° समानता का कोण है।

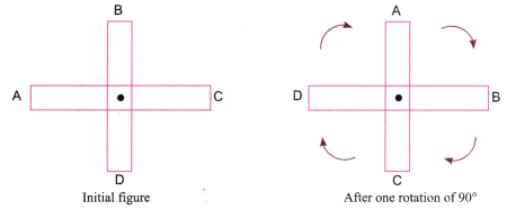
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

(ख)

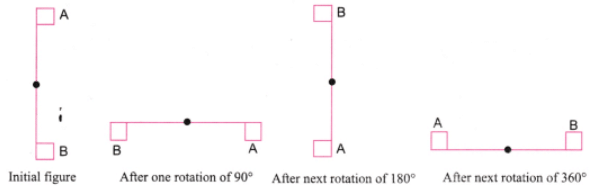
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

90° की घुमाव से ऊपर दी गई आकृति प्राप्त होती है। यह मूल आकृति के साथ ओवरलैप नहीं होती है। यह आकृति केवल एक पूरे घुमाव के बाद 360° पर अपनी मूल स्थिति में लौटती है। इसलिए, 360° समानता का कोण है।

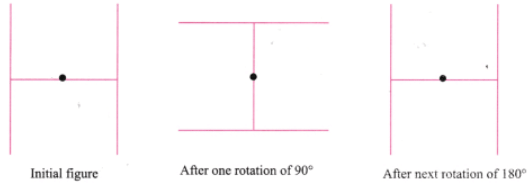
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

180° की घुमाव के बाद आकृति बिल्कुल समान है। इसलिए, 180° समानता का कोण है। प्रश्न 2: निम्नलिखित आकृतियों में से कौन सी आकृतियों में एक से अधिक समानता के कोण हैं? उत्तर: (ग) को छोड़कर सभी में एक से अधिक समानता के कोण हैं।

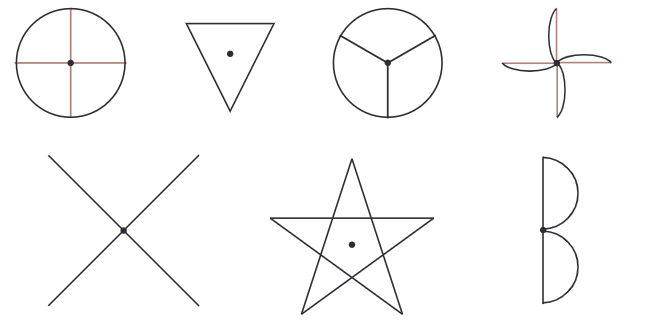
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

पृष्ठ 236

प्रश्न 3: प्रत्येक आकृति के लिए घूर्णन समानता का क्रम दें: उत्तर: क्रम: 2, 1, 6, 3, 4, 5

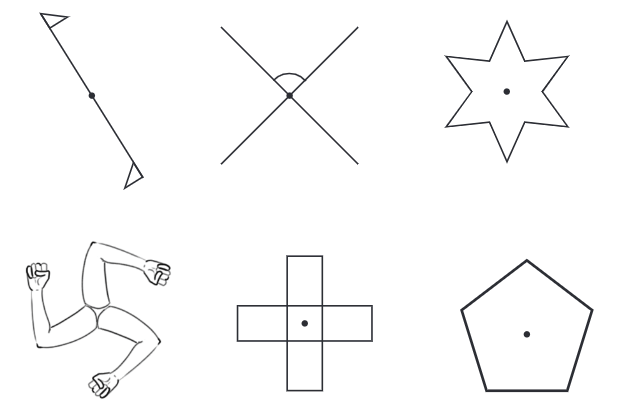
सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न: प्रत्येक मामले में, कोण सबसे छोटे कोण के गुणांक हैं। क्या आप सोचते हैं कि क्या यह हमेशा होगा? आपका क्या ख्याल है?

सत्य या असत्य

प्रश्न 1: हर आकृति के लिए 360 डिग्री एक समानता का कोण होगा।

प्रश्न 2: यदि किसी आकृति का सबसे छोटा समानता का कोण एक प्राकृतिक संख्या है, तो यह 360 का गुणांक है।

पृष्ठ 238

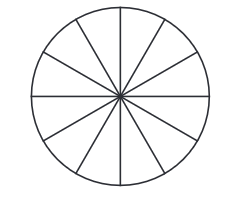
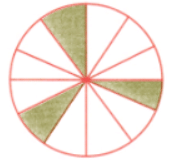
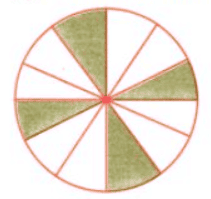
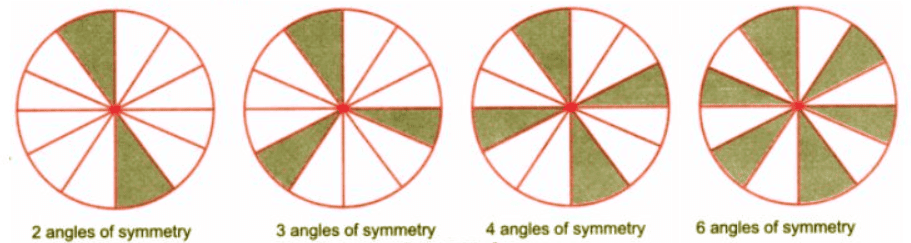
प्रश्न 1: नीचे दिए गए वृत्त के क्षेत्रों को रंग दें ताकि आकृति में i) 3 समानता के कोण हों, ii) 4 समानता के कोण हों, iii) अलग-अलग तरीकों से क्षेत्रों को रंग कर आप कितने संभावित समानता के कोण प्राप्त कर सकते हैं? उत्तर: i) यह हर 120° की घुमाव के बाद समान लगेगा।

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

ii) यह हर 90° की घुमाव के बाद समान दिखेगा। iii) चार तरीके संभव हैं।

प्रश्न 2: एक वृत्त और एक वर्ग के अलावा दो आकृतियाँ बनाएँ जो दोनों परावर्तन समरूपता और घूर्णन समरूपता रखती हैं। उत्तर:

प्रश्न 3: जहाँ भी संभव हो, एक मोटा चित्र बनाएँ:

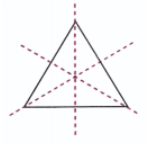
a. एक त्रिकोण जिसमें कम से कम दो समरूपता की रेखाएँ और कम से कम दो समरूपता के कोण हों। उत्तर:

b. एक त्रिकोण जिसमें केवल एक समरूपता की रेखा है लेकिन घूर्णन समरूपता नहीं है। उत्तर:

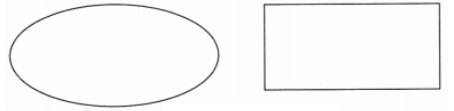
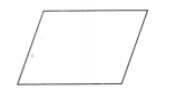
c. एक चतुर्भुज जिसमें घूर्णन समरूपता है लेकिन परावर्तन समरूपता नहीं है। उत्तर:

d. एक चतुर्भुज जिसमें परावर्तन समरूपता है लेकिन घूर्णन समरूपता नहीं है। उत्तर:

प्रश्न 4: एक आकृति में, 60° सबसे छोटा समरूपता का कोण है। इस आकृति के अन्य समरूपता के कोण क्या हैं? उत्तर: चूँकि 60° सबसे छोटा कोण है, अन्य कोण जो 60° के गुणज हैं, 360° तक समरूपता के कोण हैं। यहाँ कोण हैं 120°, 180°, 240°, 300°, 360°।

प्रश्न 5: एक आकृति में, 60° एक समरूपता का कोण है। आकृति में 60° से छोटे दो समरूपता के कोण हैं। इसका सबसे छोटा समरूपता का कोण क्या है? उत्तर: सबसे छोटा समरूपता का कोण = 60° ÷ 3 = 20°।

प्रश्न 6: क्या हम एक आकृति प्राप्त कर सकते हैं जिसमें घूर्णन समरूपता हो और जिसका सबसे छोटा समरूपता का कोण हो:

a. 45° उत्तर: हाँ, क्योंकि 360, 45 से विभाज्य है।

b. 17° उत्तर: नहीं, क्योंकि 360, 17 से विभाज्य नहीं है।

पृष्ठ 239

प्रश्न 7: यह नई संसद भवन की तस्वीर है। a. क्या तस्वीर की बाहरी सीमा में परावर्तन समरूपता है? यदि हाँ, तो समरूपता की रेखाएँ बनाइए। कितनी हैं? उत्तर: बाहरी सीमा अपने केंद्र के चारों ओर घूर्णन समरूपता दिखाती है। सबसे छोटा घूर्णन कोण = 360° ÷ 3 = 120°। अन्य घूर्णन कोण हैं 240° और 360°।

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

b. क्या इसका केंद्र के चारों ओर घूर्णन सममिति है? यदि हाँ, तो घूर्णन सममिति के कोण ज्ञात करें। उत्तर: बाहरी सीमा में परावर्तन सममिति है। इसमें 3 सममिति रेखाएँ हैं।

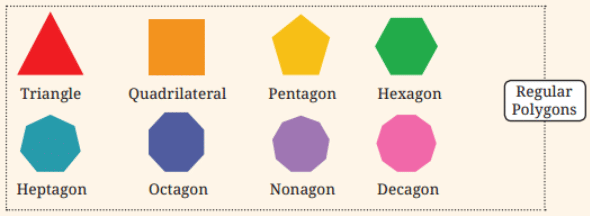
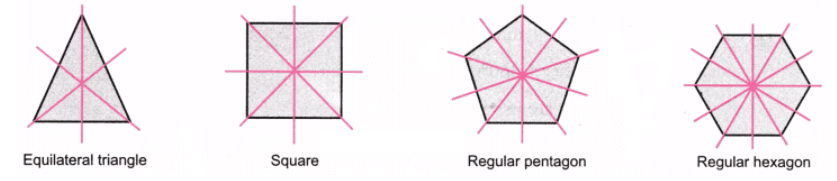
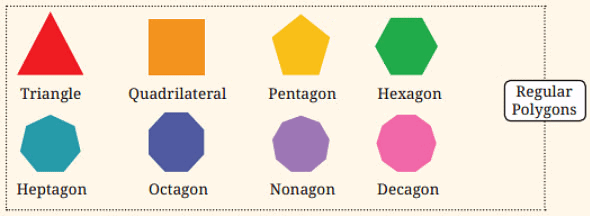
प्रश्न 8: अध्याय 1, तालिका 3 में पहले आकार अनुक्रम में नियमित बहुभुजों के आकारों में कितनी सममिति रेखाएँ हैं? आपको कौन-सा संख्या अनुक्रम मिलता है? उत्तर:

  • 3 भुजाओं वाला नियमित बहुभुज (समान भुजाकार त्रिकोण) में 3 सममिति रेखाएँ हैं।
  • 4 भुजाओं वाला नियमित बहुभुज (वर्ग) में 4 सममिति रेखाएँ हैं।
  • 5 भुजाओं वाला नियमित बहुभुज (नियमित पेंटागन) में 5 सममिति रेखाएँ हैं।
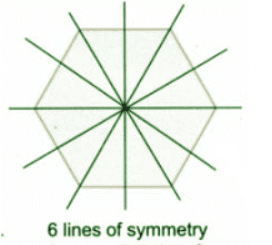
  • 6 भुजाओं वाला नियमित बहुभुज (नियमित हेक्सागन) में 6 सममिति रेखाएँ हैं।

हम निम्नलिखित पैटर्न देखते हैं: नियमित बहुभुज में भुजाओं की संख्या = सममिति रेखाओं की संख्या। संख्या अनुक्रम: 3, 4, 5, 6, 7, ………………………

प्रश्न 9: अध्याय 1, तालिका 3 में पहले आकार अनुक्रम में नियमित बहुभुजों के आकारों में कितने सममिति कोण हैं? आपको कौन-सा संख्या अनुक्रम मिलता है? उत्तर: सममिति कोणों की संख्या = सममिति रेखाओं की संख्या। इसलिए हमें संख्या अनुक्रम मिलता है: 3, 4, 5, 6, 7, ………..

प्रश्न 10: अध्याय 1, तालिका 3 में अंतिम आकार अनुक्रम में कोच स्नोफ्लेक के आकारों में कितनी सममिति रेखाएँ हैं? कितने सममिति कोण हैं? उत्तर:

प्रश्न 11: अशोक चक्र में कितनी सममिति रेखाएँ और सममिति कोण हैं? उत्तर: अशोक चक्र में 24 समान रूप से फैले हुए spokes हैं। 24 spokes 12 जोड़े बनाते हैं। विपरीत जोड़े के माध्यम से जो रेखा है वह एक सममिति रेखा है। इसलिए, कुल 12 सममिति रेखाएँ हैं। सबसे छोटा सममिति कोण = 360° ÷ 12 = 30°। अन्य सममिति कोण इसके गुणांक हैं, जो 360 तक हैं। अन्य कोण हैं 60°, 120°, 150°, ………… , 360°। (कुल 12 कोण)।

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

टाइल्स के साथ खेलना

(क) पुस्तक के अंत में दिए गए रंगीन टाइल्स का उपयोग करके निम्नलिखित आकृति को पूरा करें ताकि इसमें ठीक 2 रेखाएँ समरूपता (symmetry) हों।

(ख) 16 ऐसी टाइल्स का उपयोग करके आकृतियाँ बनाएं जिनमें ठीक:

  • 1 रेखा समरूपता हो,
  • 2 रेखाएँ समरूपता हों।

(ग) इन टाइल्स का उपयोग करके रचनात्मक समरूप डिज़ाइन बनाएं।

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6
The document सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.
All you need of Class 6 at this link: Class 6
236 docs
Join Course for Free
About this Document
Oct 02, 2025 Last updated
Related Exams
Document Description: NCERT Solutions: सममिति for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for NCERT Solutions: सममिति have been prepared according to the Class 6 exam syllabus. Information about NCERT Solutions: सममिति covers topics like समझें and NCERT Solutions: सममिति Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for NCERT Solutions: सममिति.
Introduction of NCERT Solutions: सममिति in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & NCERT Solutions: सममिति in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6
Description
Full syllabus notes, lecture & questions for सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download
Information about NCERT Solutions: सममिति
In this doc you can find the meaning of NCERT Solutions: सममिति defined & explained in the simplest way possible. Besides explaining types of NCERT Solutions: सममिति theory, EduRev gives you an ample number of questions to practice NCERT Solutions: सममिति tests, examples and also practice Class 6 tests
Explore Courses for Class 6 exam
Related Searches

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

,

video lectures

,

study material

,

Summary

,

practice quizzes

,

Sample Paper

,

Semester Notes

,

Previous Year Questions with Solutions

,

Exam

,

ppt

,

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

,

shortcuts and tricks

,

Objective type Questions

,

pdf

,

MCQs

,

mock tests for examination

,

past year papers

,

Free

,

Extra Questions

,

Important questions

,

Viva Questions

,

सममिति NCERT Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

;
Additional Information about NCERT Solutions: सममिति for Class 6 Preparation

NCERT Solutions: सममिति Free PDF Download

The NCERT Solutions: सममिति is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the NCERT Solutions: सममिति now and kickstart your journey towards success in the Class 6 exam.

Importance of NCERT Solutions: सममिति

The importance of NCERT Solutions: सममिति cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

NCERT Solutions: सममिति Notes

NCERT Solutions: सममिति Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to NCERT Solutions: सममिति. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, NCERT Solutions: सममिति Notes on EduRev are your ultimate resource for success.

NCERT Solutions: सममिति Class 6 Questions

The "NCERT Solutions: सममिति Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study NCERT Solutions: सममिति on the App

Students of Class 6 can study NCERT Solutions: सममिति alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the NCERT Solutions: सममिति, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of NCERT Solutions: सममिति is prepared as per the latest Class 6 syllabus.
© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily