Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > Word Problems: सममिति

Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

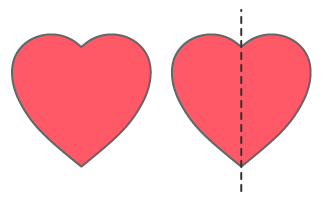
प्रश्न 1: रिया एक कार्ड के लिए दिल का आकार बनाती है। वह इसे बीच से लंबवत मोड़ती है, और दोनों आधे एकदम मेल खाते हैं। क्या लंबवत मोड़ सममिति की रेखा है? उत्तर: चूंकि दिल को बीच से लंबवत मोड़ने पर दोनों आधे एकदम मेल खाते हैं, इसलिए यह मोड़ सममिति की रेखा है। उत्तर: हाँ, लंबवत मोड़ सममिति की रेखा है।

प्रश्न 2: सिया 4 समान विकर्ण भुजाओं के साथ एक लोगो डिजाइन करती है। सबसे छोटा घूर्णन सममिति का कोण क्या है? उत्तर: 4 समान विकर्ण भुजाओं के साथ, आकार की घूर्णन सममिति का क्रम 4 है। सबसे छोटा कोण 360° ÷ 4 = 90° है। उत्तर: सबसे छोटा कोण 90° है।

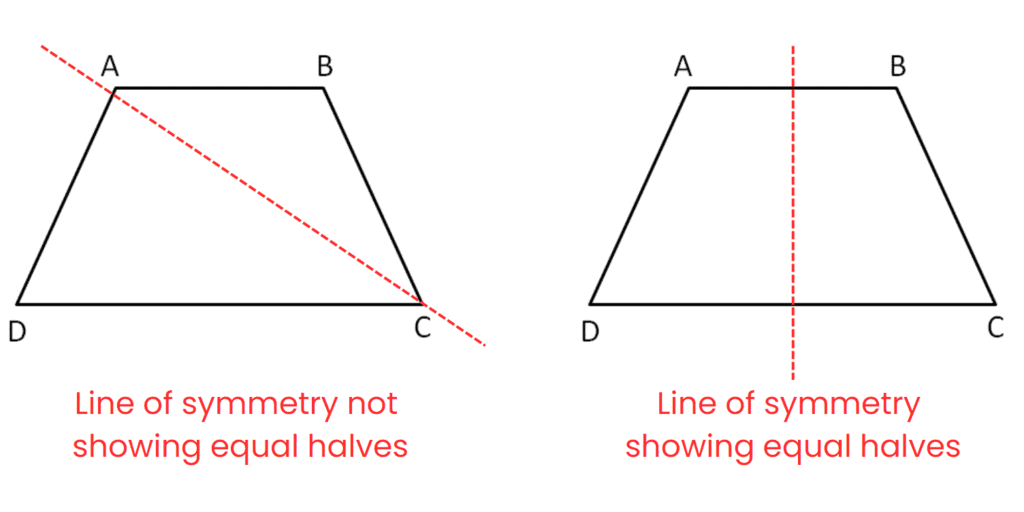
प्रश्न 3: अर्जुन एक त्रैपेज़ियम बनाता है जिसमें केवल एक जोड़ी समानांतर भुजाएँ होती हैं। वह इसे आड़ा मोड़ने की कोशिश करता है, लेकिन आधे मेल नहीं खाते। क्या त्रैपेज़ियम में आड़ा सममिति की रेखा है? उत्तर: सममिति की रेखा होने के लिए, उसके साथ मोड़ने पर मेल खाने वाले आधे हिस्से बनने चाहिए। चूंकि आड़ा मोड़ने पर आधे मेल नहीं खाते, यह सममिति की रेखा नहीं है। उत्तर: नहीं, त्रैपेज़ियम में आड़ा सममिति की रेखा नहीं है।

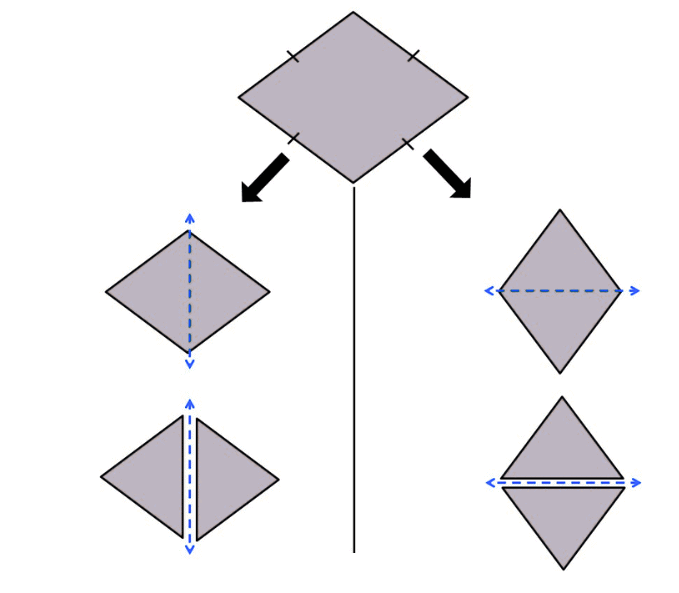
प्रश्न 4: लिला एक वर्ग के कागज़ को दोनों विकर्णों के साथ मोड़ती है और एक आकृति काटती है। अनमोल आकृति में कितनी सममिति की रेखाएँ होंगी? उत्तर: एक वर्ग के दोनों विकर्णों के साथ मोड़ने और काटने से एक आकृति बनती है जिसमें दोनों विकर्णों के साथ सममिति होती है, जिससे 2 सममिति की रेखाएँ मिलती हैं। अतिरिक्त कटौती इसे बनाए रख सकती है, लेकिन न्यूनतम 2 हैं। उत्तर: आकृति में कम से कम 2 सममिति की रेखाएँ होंगी।

प्रश्न 5: मीरा एक पैटर्न बनाती है जो एक समांतर चतुर्भुज के आकार में है। उसके पतंग में कितनी सममिति की रेखाएँ हैं? उत्तर: एक समांतर चतुर्भुज में अपने विकर्णों के साथ 2 सममिति की रेखाएँ होती हैं, क्योंकि किसी एक विकर्ण के साथ मोड़ने पर मेल खाने वाले आधे हिस्से बनते हैं। उत्तर: समांतर चतुर्भुज के आकार में बने पतंग में 2 सममिति की रेखाएँ हैं।

प्रश्न 6: अरव ने एक नियमित पंचकोण टाइल डिज़ाइन किया है। इस टाइल के घूर्णन समरूपता के कोण क्या हैं? समाधान: एक नियमित पंचकोण में 5 भुजाएँ होती हैं, इसलिए घूर्णन समरूपता का क्रम 5 है। कोण हैं 360° ÷ 5 = 72°, तो 72°, 144°, 216°, 288°, और 360°। उत्तर: कोण हैं 72°, 144°, 216°, 288°, और 360°।

प्रश्न 7: विक्रम ने 5 समान रूप से फैली पंखों वाला एक पिनव्हील डिज़ाइन किया है। यह पूर्ण 360° घूर्णन के दौरान कितनी बार समान दिखाई देता है? समाधान: 5 समान रूप से फैले पंखों वाला आकार घूर्णन समरूपता के क्रम 5 के साथ है, क्योंकि यह 360° के घूर्णन में 5 बार समान दिखाई देता है (हर 360° ÷ 5 = 72°)। उत्तर: यह 5 बार समान दिखाई देता है।

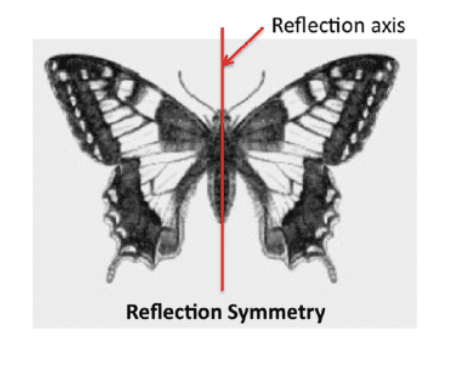
प्रश्न 8: कुणाल ने एक तितली के पंखों को देखा और नोट किया कि बाईं ओर का पंख दाएं पंख का एक दर्पण चित्र है जब इसे ऊर्ध्वाधर रूप से मोड़ा जाता है। क्या तितली में परावर्तन समरूपता है? समाधान: चूंकि बाईं ओर का पंख दाईं ओर के पंख का एक दर्पण चित्र है, तितली में परावर्तन समरूपता है। उत्तर: हाँ, तितली में परावर्तन समरूपता है।

प्रश्न 9: सारा ने विभिन्न लंबाई के भुजाओं वाला एक स्केलिन त्रिकोण बनाया। क्या वह इसे मोड़कर एक आधे का दर्पण चित्र दूसरे पर बना सकती है? समाधान: एक स्केलिन त्रिकोण में कोई भी भुजाएँ या कोण समान नहीं होते, इसलिए कोई भी मोड़ एक दर्पण चित्र नहीं बनाएगा। इसलिए, इसमें परावर्तन समरूपता नहीं है। उत्तर: नहीं, स्केलिन त्रिकोण में परावर्तन समरूपता नहीं है।

प्रश्न 10: नेहा ने 6 समान भुजाओं वाला एक तारा बनाया। उसके तारे के घूर्णन समरूपता के कोण क्या हैं? समाधान: 6 समान भुजाओं वाला तारा घूर्णन समरूपता के क्रम 6 के साथ है। कोण हैं 360° ÷ 6 = 60°, तो समरूपता के कोण हैं 60°, 120°, 180°, 240°, 300°, और 360°। उत्तर: कोण हैं 60°, 120°, 180°, 240°, 300°, और 360°।

प्रश्न 11: प्रिया एक नियमित अष्टकोण का स्केच बनाती है। इसके घूर्णन समरूपता का क्रम क्या है? हल: एक नियमित अष्टकोण में 8 भुजाएँ होती हैं, इसलिए यह 360° के घूर्णन के दौरान 8 बार समान दिखता है (हर 360° ÷ 8 = 45°)। घूर्णन समरूपता का क्रम 8 है। उत्तर: क्रम 8 है।

प्रश्न 12: तारा एक पेपर को आधा मोड़ती है, एक तरफ स्याही गिराती है, और एक डिज़ाइन बनाने के लिए इसे दबाती है। क्या परिणामी आकृति में रेखा समरूपता होगी? हल: जब इसे दबाया जाता है, तो स्याही मोड़ रेखा के पार एक दर्पण छवि बनाने के लिए फैलती है। इसलिए, परिणामी आकृति में मोड़ के साथ रेखा समरूपता होती है। उत्तर: हाँ, आकृति में रेखा समरूपता होगी।

प्रश्न 13: सानिया एक पेपर को दो बार मोड़ती है और मोड़ा हुआ रहते हुए एक पैटर्न काटती है। जब उसे खोला जाता है, तो क्या डिज़ाइन में घूर्णन समरूपता होगी? हल: दो बार मोड़ने (जैसे चौथाई में) और काटने से एक ऐसा पैटर्न बनता है जो खोले जाने पर हर 90° पर दोहराता है, जिससे घूर्णन समरूपता का क्रम 4 (कोण 90°, 180°, 270°, 360°) मिलता है। उत्तर: हाँ, डिज़ाइन में घूर्णन समरूपता होगी।

प्रश्न 14: सिमरन एक सूरजमुखी का अवलोकन करती है जिसमें पंखुड़ियाँ केंद्र के चारों ओर समान रूप से व्यवस्थित हैं। क्या इसमें घूर्णन समरूपता है? हल: सूरजमुखी की पंखुड़ियाँ रेडियल तरीके से व्यवस्थित होती हैं, इसलिए यह कुछ घूर्णनों के बाद समान दिखता है (जैसे, यदि इसमें 20 पंखुड़ियाँ हैं, तो हर 360° ÷ 20 = 18°)। इसलिए, इसमें घूर्णन समरूपता है। उत्तर: हाँ, इसमें घूर्णन समरूपता है।

प्रश्न 15: रितु एक पत्ते को देखती है जिसमें एक केंद्रीय नस होती है जहाँ दोनों तरफ दर्पण छवियाँ होती हैं। पत्ते में कितनी रेखाएँ समरूपता हैं? हल: यदि पत्ते के दोनों तरफ केंद्रीय नस के साथ दर्पण छवियाँ हैं, तो पत्ते में नस के साथ एक रेखा समरूपता है। उत्तर: पत्ते में 1 रेखा समरूपता है।

प्रश्न 16: निशा एक वृत्ताकार बैज डिज़ाइन करती है। इसमें कितनी समरूपता की रेखाएँ होती हैं? हल: एक वृत्त में अनंत समरूपता की रेखाएँ होती हैं, क्योंकि इसका केंद्र (डायामीटर) किसी भी रेखा के माध्यम से जाने पर एक दर्पण छवि उत्पन्न करता है। उत्तर: इसमें अनंत समरूपता की रेखाएँ होती हैं।

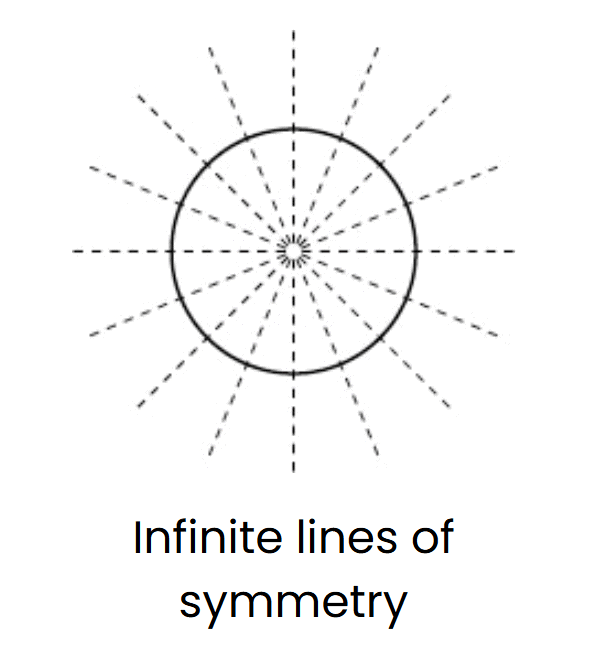
प्रश्न 17: संजना एक वृत्ताकार प्लेट को 45° घुमाती है। क्या यह अभी भी वैसी ही दिखती है, जो घूर्णन समरूपता को दर्शाता है? हल: एक वृत्त में अनंत घूर्णन समरूपता होती है, क्योंकि यह अपने केंद्र के चारों ओर किसी भी कोण पर घुमाने के बाद वैसी ही दिखती है। इसलिए, 45° का घुमाव इसे अपरिवर्तित रखता है। उत्तर: हाँ, यह वैसी ही दिखती है, जो घूर्णन समरूपता को दर्शाता है।

प्रश्न 18: दिव्या एक पेपर स्नोफ्लेक बनाती है, जिसमें वह एक वृत्त को 8 समान भागों में मोड़कर पैटर्न काटती है। स्नोफ्लेक में कितनी समरूपता की रेखाएँ होंगी? हल: एक वृत्त को 8 समान भागों में मोड़ने और काटने से एक स्नोफ्लेक बनता है जिसमें 8 समरूपता की रेखाएँ होती हैं, प्रत्येक मोड़ रेखा के माध्यम से केंद्र के साथ। उत्तर: स्नोफ्लेक में 8 समरूपता की रेखाएँ होती हैं।

The document Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: Word Problems: सममिति for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for Word Problems: सममिति have been prepared according to the Class 6 exam syllabus. Information about Word Problems: सममिति covers topics like and Word Problems: सममिति Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Word Problems: सममिति.

Introduction of Word Problems: सममिति in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & Word Problems: सममिति in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about Word Problems: सममिति

In this doc you can find the meaning of Word Problems: सममिति defined & explained in the simplest way possible. Besides explaining types of Word Problems: सममिति theory, EduRev gives you an ample number of questions to practice Word Problems: सममिति tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

past year papers

practice quizzes

Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Exam

Summary

Viva Questions

Previous Year Questions with Solutions

ppt

Semester Notes

mock tests for examination

study material

Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Sample Paper

Word Problems: सममिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Objective type Questions

Free

Extra Questions

video lectures

pdf

MCQs

shortcuts and tricks

Important questions

;

Additional Information about Word Problems: सममिति for Class 6 Preparation

Word Problems: सममिति Free PDF Download

The Word Problems: सममिति is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Word Problems: सममिति now and kickstart your journey towards success in the Class 6 exam.

Importance of Word Problems: सममिति

The importance of Word Problems: सममिति cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Word Problems: सममिति Notes

Word Problems: सममिति Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Word Problems: सममिति. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Word Problems: सममिति Notes on EduRev are your ultimate resource for success.

Word Problems: सममिति Class 6 Questions

The "Word Problems: सममिति Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Word Problems: सममिति on the App

Students of Class 6 can study Word Problems: सममिति alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Word Problems: सममिति, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Word Problems: सममिति is prepared as per the latest Class 6 syllabus.

Education Revolution