कक्षा 6 गणित: नमूना पत्र समाधान - 3 | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

सामान्य निर्देश

सभी प्रश्न अनिवार्य हैं।

• अनुभाग A में 12 प्रश्न हैं, प्रत्येक 1 अंक के लिए।
• अनुभाग B में 10 प्रश्न हैं, प्रत्येक 2 अंक के लिए।
• अनुभाग C में 8 प्रश्न हैं, प्रत्येक 3 अंक के लिए।
• अनुभाग D में 2 प्रश्न हैं, प्रत्येक 5 अंक के लिए।

Q1: एक आयत का परिमाप इस प्रकार से गणना की जाती है: (1 अंक)
(a) लंबाई × चौड़ाई
(b) 2 × (लंबाई + चौड़ाई)
(c) (लंबाई × चौड़ाई) / 2
(d) लंबाई × चौड़ाई × 2

उत्तर: (b)

Q2: एक लिफ्ट 6वीं मंजिल पर है। यह 10 मंजिल नीचे जाती है। अब यह किस मंजिल पर है? (1 अंक)
(a) 16वीं मंजिल
(b) -4वीं मंजिल
(c) 4वीं मंजिल
(d) -10वीं मंजिल

उत्तर: (b)

Q3: यदि एक आकृति 180° एक निश्चित बिंदु के चारों ओर घुमाई जाती है और वही दिखती है, तो इसमें है: (1 अंक)
(a) परावर्तन समरूपता
(b) रेखा समरूपता
(c) घूर्णन समरूपता क्रम 2
(d) कोई समरूपता नहीं

उत्तर: (c)

Q4: मिश्रित भिन्न को एक अनुपयुक्त भिन्न में परिवर्तित करें। (1 अंक)
(a) 15/5
(b) 16/5
(c) 17/5
(d) 14/5

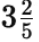
उत्तर: (c)

Q5: 60 का गुणनखंड क्या है? (1 अंक)
(a) 2 × 2 × 3 × 5
(b) 2 × 3 × 5
(c) 2 × 2 × 5 × 7
(d) 3 × 3 × 5

उत्तर: (a)

Q6: एक त्रिकोण की आधार 10 सेमी और ऊँचाई 6 सेमी है। इसका क्षेत्रफल क्या है? (1 अंक)
(a) 30 सेमी²
(b) 60 सेमी²
(c) 16 सेमी²
(d) 40 सेमी²

उत्तर: (a)

Q7: निम्नलिखित में से किस आकृति में अनंत समरूपता की रेखाएँ हैं? (1 अंक)
(a) वर्ग
(b) आयत
(c) वृत्त
(d) त्रिकोण

Q8: एक शहर में रात को तापमान -12°C दर्ज किया गया और सुबह यह 15°C बढ़ गया। सुबह का तापमान क्या होगा? (1 अंक) (क) -3°C (ख) 3°C (ग) -27°C (घ) 27°C

Q9: निम्नलिखित में से कौन सा एक सीधा कोण है? (1 अंक) (क) 45° (ख) 90° (ग) 180° (घ) 360°

Q10: दो संख्याएँ सह-प्राइम तब होती हैं जब उनके पास: (1 अंक) (क) 1 के अलावा कोई सामान्य गुणक नहीं (ख) कम से कम एक सामान्य गुणक (ग) केवल सम गुणक (घ) केवल विषम गुणक

Q11: कौन सा भिन्न 3/7 के समकक्ष है? (1 अंक) (क) 6/14 (ख) 5/14 (ग) 3/14 (घ) 4/7

Q12: निम्नलिखित में से कौन सा कथन बार ग्राफ के बारे में सही है? (1 अंक) (क) इनमें भिन्न चौड़ाई की पट्टियाँ होती हैं (ख) पट्टियों की ऊँचाई या लंबाई आवृत्ति का प्रतिनिधित्व करती है (ग) पट्टियाँ हमेशा क्षैतिज होनी चाहिए (घ) बार ग्राफ को स्केल की आवश्यकता नहीं होती

उत्तर: (ख)

Q13: 2, 5, 9, 14, 20, ... को पेंटागोनल संख्या क्यों कहा जाता है? 1, 6, 12, 18, 24, ... को हेक्सागोनल संख्या क्यों कहा जाता है? 1, 4, 10, 20, 35, ... को टेट्राहेड्रल संख्या क्यों कहा जाता है? (2 अंक)

• पेंटागोनल संख्या: इन संख्याओं को बढ़ते स्तरों में बिंदुओं को रखकर एक पेंटागन के आकार में व्यवस्थित किया जा सकता है।
• हेक्सागोनल संख्या: इन संख्याओं को फैलते हेक्सागोनल पैटर्न में बिंदुओं को रखकर एक हेक्सागोन के आकार में व्यवस्थित किया जा सकता है।
• टेट्राहेड्रल संख्या: इन संख्याओं को तीन-आयामी पिरामिड स्तरों में बिंदुओं को रखकर एक टेट्राहेड्रन के आकार में व्यवस्थित किया जा सकता है।

Q14: निम्नलिखित संख्याओं को विभाजित करने पर प्राप्त शेषफल ज्ञात करें (2 अंक)

(i) 85

उत्तर:

• 10 से विभाजित: शेषफल = 5
• 5 से विभाजित: शेषफल = 0
• 2 से विभाजित: शेषफल = 1

(ii) 102

उत्तर:

• 10 से विभाजित: शेष = 2
• 5 से विभाजित: शेष = 2
• 2 से विभाजित: शेष = 0

प्रश्न 15: निम्नलिखित संख्याओं को संख्या रेखा पर बढ़ते क्रम में व्यवस्थित करें: 1920, 3840, 2760, 4680। (2 अंक)

उत्तर: सबसे छोटी से सबसे बड़ी: 1920, 2760, 3840, 4680।

• 1920 2000 के करीब है।
• 2760 2700 के ठीक बाद आता है।
• 3840 3800 के थोड़ा आगे है।
• 4680 4700 के करीब है।

बढ़ते क्रम में सही अनुक्रम है: 1920, 2760, 3840, 4680।

प्रश्न 16: लंबाई 1/5 के कितने टुकड़े 2/3 की लंबाई बनाएंगे? (2 अंक)

उत्तर: कुल टुकड़ों की संख्या = इसलिए, 1/5 की लंबाई के 3 पूर्ण टुकड़े 2/3 की लंबाई के करीब बनाएंगे, और चौथे टुकड़े का एक छोटा हिस्सा आवश्यक है।

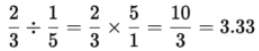
प्रश्न 17: एक त्रिकोण के तीन भुजाएँ 5 सेमी, 6 सेमी, और 7 सेमी की माप की हैं। इसका परिमाप खोजें। (2 अंक)

उत्तर: त्रिकोण का परिमाप = सभी भुजाओं का योग = 5 + 6 + 7 = 18 सेमी

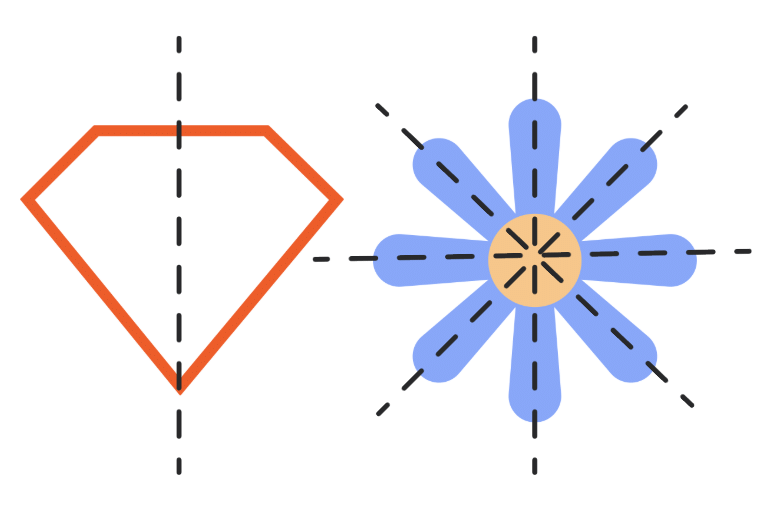
प्रश्न 18: क्या आप नीचे दिए गए आकृतियों में कोई समरूपता की रेखा देख रहे हैं? (2 अंक)

उत्तर: हीरे के आकार में एक समरूपता की रेखा है और दिए गए फूल में 4 समरूपता की रेखाएँ हैं।

प्रश्न 19: अंकों 2, 5, और 7 का उपयोग करके एक चार अंकीय पलिंड्रोम बनाएं, और बताएं कि यह क्यों काम करता है। (2 अंक)

उत्तर: 2552 एक पलिंड्रोम है क्योंकि यह आगे और पीछे एक समान पढ़ता है: 2-5-5-2, जिसमें पहले और अंतिम अंक मेल खाते हैं (2), और दूसरे और तीसरे अंक मेल खाते हैं (5)।

प्रश्न 20: अनुक्रम का अवलोकन करें: 11, 22, 33, 44, 55। पैटर्न को अगले दो अंशों तक बढ़ाएं और बताएं। (2 अंक)

उत्तर: उपरोक्त पैटर्न में संख्याएँ हर बार 11 से बढ़ रही हैं, जहाँ अंकों को दोहराया जा रहा है। पैटर्न को बढ़ाने के लिए, अगले दो अंश होंगे:

प्रश्न 21: 2/3 और 5/7 का योग क्या है? (2 अंक)

उत्तर: 2/3 को 14/21 में बदलें (अंश और हर को 7 से गुणा करें)।

5/7 को 15/21 में बदलें (अंश और हर को 3 से गुणा करें)।

अब, दोनों भिन्नों को जोड़ें: 14/21 + 15/21 = 29/21।

इसलिए, 2/3 और 5/7 का योग 29/21 है।

प्रश्न 22: एक दर्जी 20 सेंटीमीटर के वर्गाकार मेज़पोश के चारों ओर लेस डालना चाहता है। उसने बाजार से 1 मीटर लेस खरीदी। कार्य पूरा करने के बाद उसके पास कितनी लेस बची है? (2 अंक)

उत्तर: भुजाएँ = 20 सेंटीमीटर

वर्ग का परिमाप: S × 4 = 20 × 4 = 80 सेंटीमीटर

कपड़े की लंबाई: 1 मीटर = 100 सेंटीमीटर

बची हुई लेस: 100 - 80 = 20 सेंटीमीटर

प्रश्न 23: निम्नलिखित को हल करें और रिक्त स्थान भरें (3 अंक)

• (a) (60) _______________ = 300
• (b) (80) _______________ = -250
• (c) (-90) _______________ = 150

उत्तर: (a) (60) _______________ = 300 मान लें (60) x = 300 ⇒ x = 300 - 60 = 240 ∴ (60) (240) = 300

(b) (80) _______________ = -250 मान लें (80) x = -250 ⇒ x = -250 - 80 = -330 ∴ (80) (-330) = -250

(c) (-90) _______________ = 150 मान लें (-90) x = 150 ⇒ x = 150 - (-90) = 150 + 90 = 240 ∴ (-90) (240) = 150

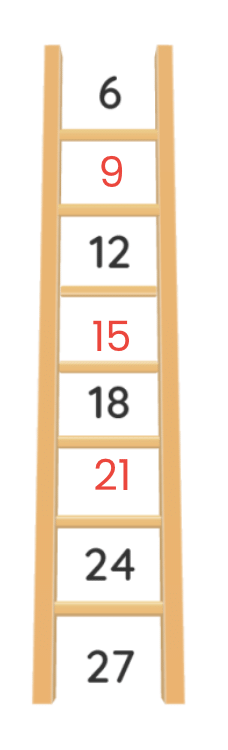
प्रश्न 24: क्या आप सीढ़ी में गायब नंबर भर सकते हैं? अपने उत्तर को उचित ठहराएं। (3 अंक)

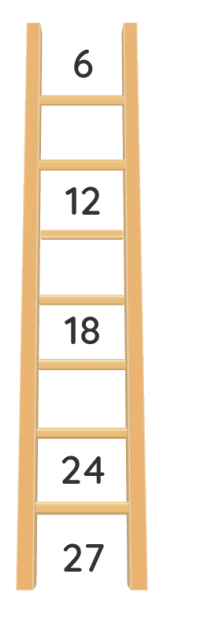
उत्तर:

दी गई अनुक्रम: 6, __, 12, __, 18, __, 24, 27, __

• 6 के बाद, 3 जोड़ने पर 9 मिलता है।
• 12 के बाद, 3 जोड़ने पर 15 मिलता है।
• 18 के बाद, 3 जोड़ने पर 21 मिलता है।
• 27 के बाद, 3 जोड़ने पर 30 मिलता है।

प्रश्न 25: भूगोल में 72 छात्रों द्वारा प्राप्त अंक निम्नलिखित हैं। इन अंकों को ताली निशान का उपयोग करके एक तालिका में व्यवस्थित करें। (3 अंक)

(क) छात्रों ने 6 से अधिक अंक प्राप्त किए। (ख) छात्रों ने 2 या उससे कम अंक प्राप्त किए।

उत्तर: चरण 1: छात्रों द्वारा प्राप्त अंकों की गणना करने के लिए, निम्नलिखित तालिका देखें:

चरण 2: उन छात्रों की संख्या जिन्होंने 6 से अधिक अंक प्राप्त किए या, उन छात्रों की संख्या जिन्होंने 7, 8, 9 अंक प्राप्त किए = 11 + 9 + 10 = 30 छात्र।

चरण 3: उन छात्रों की संख्या जिन्होंने 2 या उससे कम अंक प्राप्त किए या, उन छात्रों की संख्या जिन्होंने 2 अंक प्राप्त किए = 10 = 10 छात्र।

प्रश्न 26: चित्र की पहचान करें (3 अंक)

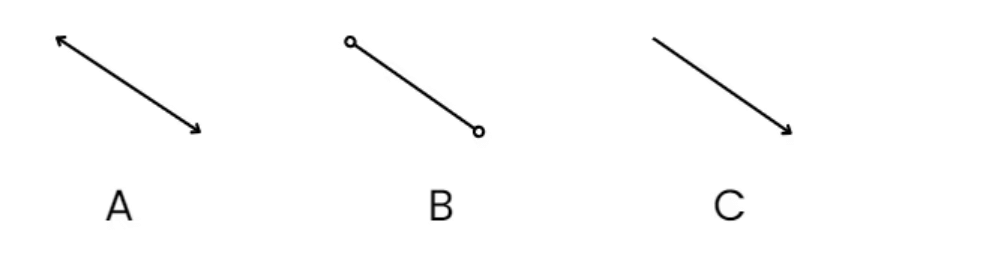
उत्तर: चित्र ए: रेखा – यह दोनों दिशाओं में अनंत तक फैली हुई है। चित्र बी: रेखा खंड – इसके दो अंत बिंदु हैं, इसलिए यह उन बिंदुओं के पार नहीं बढ़ती। चित्र सी: किरण – यह एक बिंदु से शुरू होती है और एक दिशा में अनंत तक फैली रहती है।

प्रश्न 27: चित्रग्राफ प्रश्न पढ़ें और उत्तर दें (3 अंक)

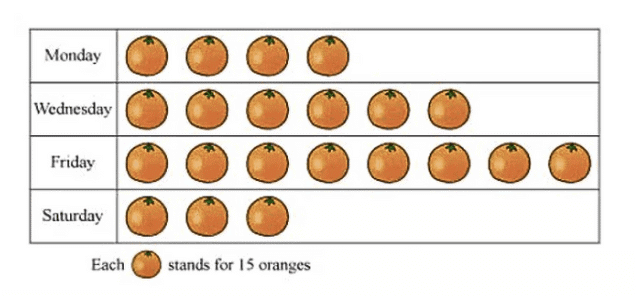
(i) सोमवार को कितने संतरे तोड़े गए? (ii) संतरे की अधिकतम संख्या कब तोड़ी गई? (iii) संतरे की अधिकतम संख्या कब तोड़ी गई?

उत्तर: (i) सोमवार को तोड़े गए संतरे = 4 x 15 = 60 संतरे। (ii) शुक्रवार। (iii) शनिवार।

प्रश्न 28: एक लिफ्ट एक इमारत में विभिन्न मंजिलों के बीच ऊपर और नीचे चलती है। बेसमेंट को नकारात्मक संख्याओं द्वारा दर्शाया जाता है, और ग्राउंड फ्लोर के ऊपर की मंजिलों को सकारात्मक संख्याओं द्वारा दर्शाया जाता है। ग्राउंड फ्लोर 0 है। (4 अंक) (A) एक लिफ्ट 5वीं मंजिल से शुरू होती है और 8 मंजिल नीचे जाती है। वह कौन सी मंजिल पर पहुंचती है? (B) उस मंजिल से, यह 6 मंजिल ऊपर जाती है। लिफ्ट अब कहाँ है? (C) यदि लिफ्ट 4 और मंजिल नीचे जाती है, तो यह किस मंजिल पर रुकेगी?

उत्तर: (A) 5वें मंजिल से शुरू करते हुए 8 मंजिल नीचे जाते हैं: 5−8=−3 लिफ्ट 3वें भूमिगत मंजिल (-3) पर पहुँचती है। (B) 6 मंजिल ऊपर जाते हैं: −3 + 6=3 लिफ्ट अब 3वें मंजिल पर है। (C) 4 मंजिल नीचे जाते हैं: 3−4=−1 लिफ्ट 1st भूमिगत मंजिल (-1) पर रुकती है।

प्रश्न 29: मान लीजिए कि आपके बैंक खाते में ₹0 है, और फिर आपके पास ₹3, ₹6, ₹12, ₹24, ₹48, ₹96 के डेबिट हैं, और फिर एक बार का क्रेडिट ₹200 है। अब आपका बैंक खाता बैलेंस क्या है? (4 अंक)

उत्तर: यहाँ, डेबिट = ₹3 + ₹6 + ₹12 + ₹24 + ₹48 + ₹96 = ₹189 ∴ बैलेंस = क्रेडिट – डेबिट = ₹200 – ₹189 = ₹11 इसलिए, आपका बैंक खाता बैलेंस ₹11 है।

प्रश्न 30: एक किसान एक आयताकार खेत में खाद डालना चाहता है, जिसकी लंबाई 500 मीटर और चौड़ाई 200 मीटर है। खाद डालने की लागत ₹8 प्रति 100 वर्ग मीटर है। पूरे खेत को खाद डालने की कुल लागत क्या होगी? (4 अंक)

उत्तर: यहाँ, लंबाई = 500 मीटर और चौड़ाई = 200 मीटर इसलिए, आयताकार खेत का क्षेत्रफल = लंबाई × चौड़ाई = 500 × 200 = 1,00,000 वर्ग मीटर

अब, 100 वर्ग मीटर खाद डालने की लागत = ₹8 कुल लागत = (8/100) × 100000 = ₹8,000

प्रश्न 31: 2032 एक लीप वर्ष है (क्योंकि फरवरी में 29 दिन हैं)। (5 अंक) लीप वर्ष उन वर्षों में होते हैं जो 4 के गुणांक होते हैं, सिवाय उन वर्षों के जो 100 से पूर्णतः विभाजित होते हैं लेकिन 400 से नहीं। (क) वर्ष 2015 से अब तक, कौन से वर्ष लीप वर्ष थे? (ख) वर्ष 2032 से 2100 तक, कितने लीप वर्ष हैं?

उत्तर: (क) वर्ष 2015 से 2032 तक, 5 लीप वर्ष हैं: 2016, 2020, 2024, 2028, और 2032। (ख) 2032 से 2099 तक के लीप वर्ष हैं: 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076, 2080, 2084, 2088, 2092, 2096। इसलिए, 2032 से 2099 तक 17 लीप वर्ष हैं।

प्रश्न 32: दिए गए आकृति का परिमाप ज्ञात कीजिए: (5 अंक)

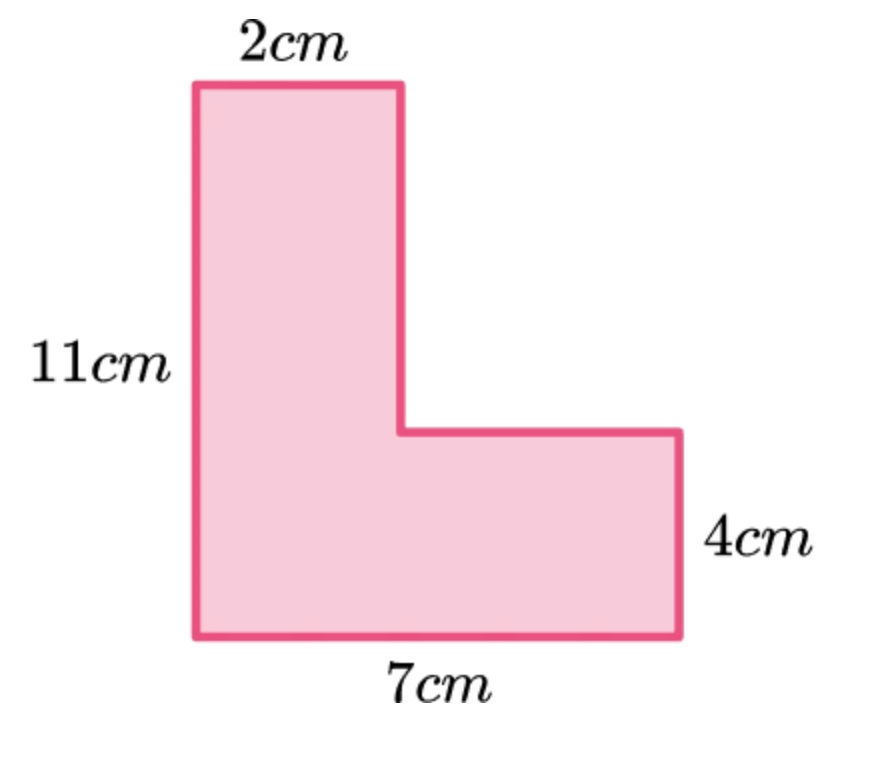
उत्तर: पहले हमें कुछ गायब लंबाईयों को ज्ञात करना होगा। हम लंबवत लंबाईयों को देख सकते हैं। गायब लंबवत लंबाई 7 सेमी है क्योंकि 11−4 = 7।

इसके बाद, हम गायब क्षैतिज लंबाई को देख सकते हैं। गायब पक्ष 5 सेमी है क्योंकि 7−2=5।

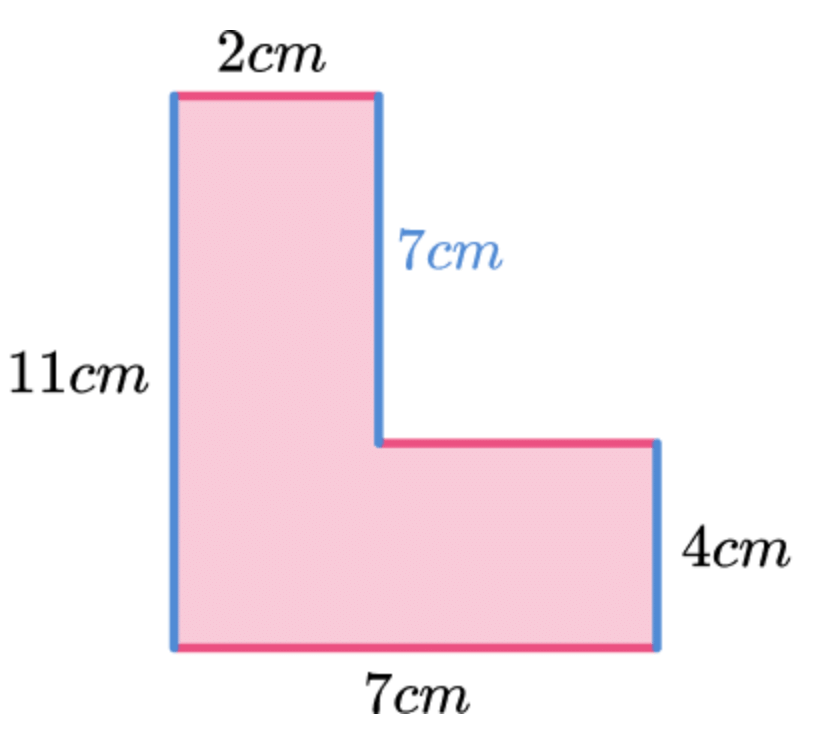
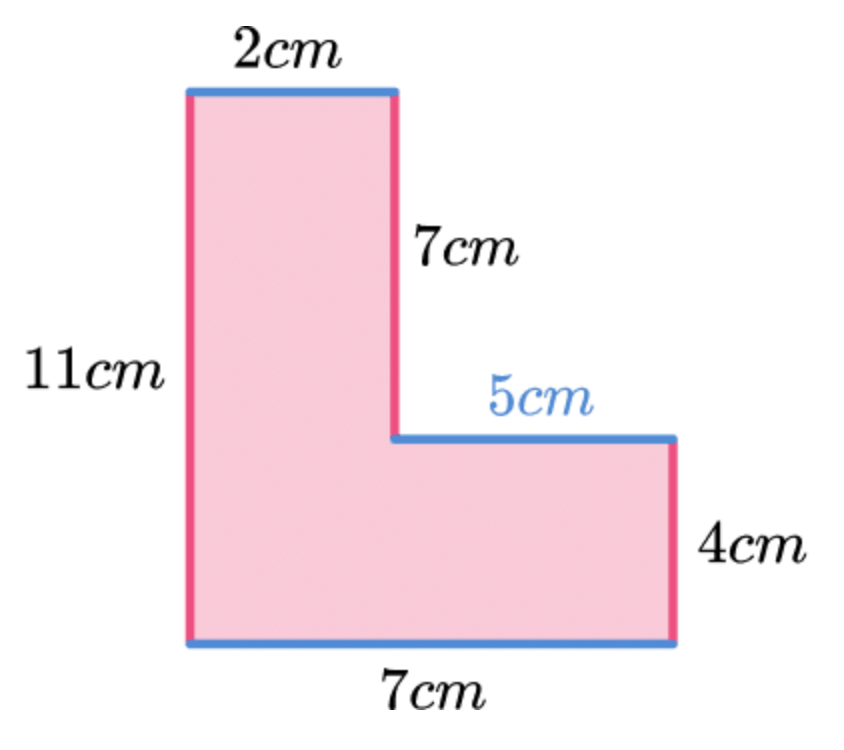
ऊपरी बाएँ कोने से शुरू करते हुए और आकृति के चारों ओर घड़ी की दिशा में चलते हुए, हम पक्षों को जोड़ सकते हैं।

2 + 7 + 5 + 4 + 7 + 11 = 36

इसलिए, परिमाप = 36 सेमी