कक्षा 6 गणित: नमूना पत्र समाधान- 5 - Class 6 PDF Download
सामान्य निर्देश
सभी प्रश्न अनिवार्य हैं।
- अनुभाग A में 12 प्रश्न हैं, प्रत्येक 1 अंक के लिए।
- अनुभाग B में 10 प्रश्न हैं, प्रत्येक 2 अंक के लिए।
- अनुभाग C में 8 प्रश्न हैं, प्रत्येक 3 अंक के लिए।
- अनुभाग D में 2 प्रश्न हैं, प्रत्येक 5 अंक के लिए।
प्रश्न 1: एक नियमित अष्टभुज में कितनी समरूपताएँ होती हैं? (1 अंक) (क) 3 (ख) 4 (ग) 8 (घ) 6
उत्तर: (ग)
प्रश्न 2: एक आयत का परिमाप 24 सेमी है। यदि लंबाई 8 सेमी है, तो चौड़ाई क्या होगी? (1 अंक) (क) 5 सेमी (ख) 8 सेमी (ग) 4 सेमी (घ) 6 सेमी
प्रश्न 3: भिन्न 7/10 में 7 को क्या कहते हैं? (1 अंक) (क) हर (ख) अंश (ग) भागफल (घ) पूर्णांक
उत्तर: (ख)
प्रश्न 4: improper भिन्न 13/5 को मिश्रित भिन्न में परिवर्तित करें। (1 अंक) (क) 2 3/5 (ख) 3 2/5 (ग) 2 1/5 (घ) 2 2/5
उत्तर: (क)
प्रश्न 5: एक शहर में सुबह का तापमान 3°C है। दोपहर तक, यह 6°C बढ़ता है। दोपहर का तापमान क्या होगा? (1 अंक) (क) 10°C (ख) 5°C (ग) 9°C (घ) 6°C
प्रश्न 6: ब्रह्मगुप्त की विधि का उपयोग करते हुए निम्नलिखित भिन्नों को जोड़ें: (1 अंक) 4/7 3/7 (क) 7/7 (ख) 1 (ग) 2/7 (घ) 3/7
उत्तर: (क)
प्रश्न 7: निम्नलिखित संख्याओं के जोड़े में से कौन से सह-प्राइम हैं? (1 अंक) (क) 8 और 16 (ख) 18 और 24 (ग) 5 और 12 (घ) 14 और 28
उत्तर: (ग)
प्रश्न 8: बार ग्राफ क्या है? (1 अंक) (क) एक ग्राफ जो चित्रों या वस्तुओं का उपयोग करके डेटा का प्रतिनिधित्व करता है (ख) एक ग्राफ जो डेटा का प्रतिनिधित्व करने के लिए बार का उपयोग करता है (ग) एक गणितीय क्रिया (घ) औसत निकालने के लिए उपयोग किया जाने वाला चार्ट
उत्तर: (b)
प्रश्न 9: एक आकृति में घूर्णनात्मक समरूपता होती है यदि इसे __ से कम कोण पर घुमाया जा सके और फिर भी यह समान दिखे। (1 अंक) (क) 120° (ख) 180° (ग) 360° (घ) 90°
उत्तर: (क)
प्रश्न 10: भिन्नों को दृश्य रूप में कहाँ प्रदर्शित किया जा सकता है? (1 अंक) (क) संख्या रेखा पर (ख) बार ग्राफ में (ग) केवल दशमलव रूप में (घ) घड़ी पर
उत्तर: (क)
प्रश्न 11: पैटर्न में लापता संख्या खोजें: (1 अंक) 150, 140, 130, __, 110 (क) 120 (ख) 125 (ग) 115 (घ) 105
उत्तर: पैटर्न लगातार पूर्ण वर्गों द्वारा बढ़ता है: 1st पंक्ति = 1² = 1 2nd पंक्ति = 2² = 4 3rd पंक्ति = 3² = 9 4th पंक्ति = 4² = 16 5th पंक्ति = 5² = 25 पाँचवीं पंक्ति में 25 कुर्सियाँ होंगी।
प्रश्न 12: एक तीव्र कोण हमेशा होता है: (1 अंक) (क) 90° से कम (ख) 90° के बराबर (ग) 90° से अधिक लेकिन 180° से कम (घ) 180° से अधिक
उत्तर: (क)
प्रश्न 13: नेहा कुर्सियों को एक वर्ग पैटर्न में व्यवस्थित कर रही है। पहली पंक्ति में 1 कुर्सी है, दूसरी पंक्ति में 4 कुर्सियाँ हैं, तीसरी पंक्ति में 9 कुर्सियाँ हैं, और चौथी पंक्ति में 16 कुर्सियाँ हैं। यदि वह इस पैटर्न को जारी रखती है, तो पाँचवीं पंक्ति में कितनी कुर्सियाँ होंगी? (2 अंक)
उत्तर: पैटर्न लगातार पूर्ण वर्गों द्वारा बढ़ता है: 1st पंक्ति = 1² = 1 2nd पंक्ति = 2² = 4 3rd पंक्ति = 3² = 9 4th पंक्ति = 4² = 16 5th पंक्ति = 5² = 25 पाँचवीं पंक्ति में 25 कुर्सियाँ होंगी।
प्रश्न 14: सबसे छोटे और सबसे बड़े 5-डिजिट पलिंड्रोम का योग क्या है? उनका अंतर क्या है? (2 अंक)
उत्तर: सबसे छोटा 5-डिजिट पलिंड्रोम = 10001 सबसे बड़ा 5-डिजिट पलिंड्रोम = 99999
योग = 10001 + 99999 = 110000 अंतर = 99999 - 10001 = 89998
प्रश्न 15: 5/8 के लिए दो समकक्ष भिन्नें लिखें। (2 अंक)
उत्तर: यहाँ, 5/8 → 5 × 2 / 8 × 2 = 10/16 5/8 → 5 × 3 / 8 × 3 = 15/24
यहाँ, 10/16, 15/24, 5/8 के समकक्ष भिन्नें हैं।
Q16: एक वर्गाकार बगीचे की एक भुज का लंबाई 12 मीटर है। इसका क्षेत्रफल ज्ञात करें। (2 अंक)
उत्तर: वर्ग का क्षेत्रफल = भुजा × भुजा = 12 × 12 = 144 वर्ग मीटर
Q17: एक आयताकार पार्क की लंबाई 50 मीटर है और इसका क्षेत्रफल 650 वर्ग मीटर है। इसकी चौड़ाई ज्ञात करें। (2 अंक)
उत्तर: लंबाई = 50 मीटर
क्षेत्रफल = 650 वर्ग मीटर
तो, प्रश्न के अनुसार: आयत का क्षेत्रफल = लंबाई × चौड़ाई 650 = 50 × चौड़ाई
= 50 × चौड़ाई = 650
चौड़ाई = 650 / 50
= चौड़ाई = 13 मीटर
Q18: निम्नलिखित आकृतियों में, l सममिति की रेखा है। आकृति को पूरा करें ताकि यह सममित हो। (2 अंक)
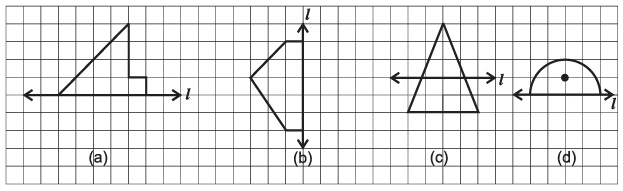
उत्तर:
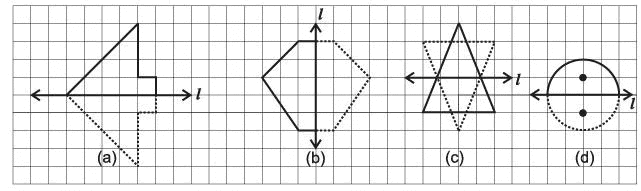
Q19: अंग्रेजी वर्णमाला के पहले दस बड़े अक्षरों पर विचार करें, उनमें से उन अक्षरों की सूची बनाएं जिनमें हैं: (i) समांतर रेखाएं (जैसे A) (ii) क्षैतिज समांतर रेखाएं (जैसे B) (iii) कोई समांतर रेखा नहीं (जैसे F) (iv) दोनों- Vertical और Horizontal समांतर रेखाएं (जैसे H)
उत्तर: (i) A, H, I (ii) B, C, D, E, H, I (iii) F, G, J (iv) H, I
Q20: क्या पहला संख्या दूसरे द्वारा विभाजित है? प्राथमिक गुणनखंड का उपयोग करें। (2 अंक)
(a) 240 और 60
उत्तर: 240 का प्राथमिक गुणनखंड 2 × 2 × 2 × 2 × 3 × 5 है, और 60 का प्राथमिक गुणनखंड 2 × 2 × 3 × 5 है। चूंकि 240 में 60 के सभी गुणक हैं, यह 60 से विभाजित है। हाँ, 240 60 से विभाजित है।
(b) 1024 और 32
उत्तर: 1024 का प्राथमिक गुणनखंड 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 है, और 32 का प्राथमिक गुणनखंड 2 × 2 × 2 × 2 × 2 है। चूंकि 1024 में 32 के सभी गुणक हैं, यह 32 से विभाजित है। हाँ, 1024 32 से विभाजित है।
प्रश्न 21: एक आयताकार खेल का मैदान 600 मीटर लंबा और 250 मीटर चौड़ा है। यदि सीमाओं को रंगने की लागत ₹10 प्रति 100 वर्ग मीटर है, तो पूरे सीमा को रंगने की कुल लागत क्या होगी? (3 अंक)
उत्तर: यहाँ, लंबाई = 600 मीटर और चौड़ाई = 250 मीटर। इसलिए, खेल के मैदान का क्षेत्रफल = लंबाई × चौड़ाई = 600 × 250 = 1,50,000 वर्ग मीटर।
अब, 100 वर्ग मीटर को रंगने की लागत = ₹10। कुल लागत = (10/100) × 150000 = ₹15,000।
प्रश्न 22: एक आयताकार कागज की शीट जिसमें आयाम 60 मीटर × 40 मीटर है, उसके चारों ओर 4 मीटर चौड़ी पट्टी काटी जाती है। काटी गई पट्टी का क्षेत्रफल और शेष शीट का क्षेत्रफल ज्ञात कीजिए। (3 अंक)
उत्तर: दी गई जानकारी के अनुसार, शीट की लंबाई = 60 मीटर। शीट की चौड़ाई = 40 मीटर। शीट का क्षेत्रफल = 60 × 40 = 2400 वर्ग मीटर।
शीट से चारों ओर 4 मीटर चौड़ी पट्टी काटी जाती है। मान लीजिए कि यह एक आयत PQRS बनाती है। आयत PQRS की लंबाई = 60 – 4 – 4 = 60 – 8 = 52 मीटर। आयत की चौड़ाई = 40 – 4 – 4 = 40 – 8 = 32 मीटर।
आयत PQRS का क्षेत्रफल (शेष शीट का क्षेत्रफल) = 52 × 32 = 1664 वर्ग मीटर। काटी गई पट्टी का क्षेत्रफल = शीट का क्षेत्रफल – PQRS का क्षेत्रफल = 2400 – 1664 = 736 वर्ग मीटर।
∴ काटी गई पट्टी का क्षेत्रफल = 736 वर्ग मीटर।
प्रश्न 23: निम्नलिखित संख्याओं/अभिव्यक्तियों को संख्या रेखा पर दर्शाएं। (3 अंक) (i) –7 (ii) 3 (–4) (iii) 4 6
उत्तर:
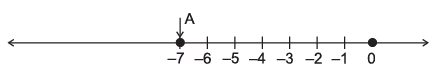
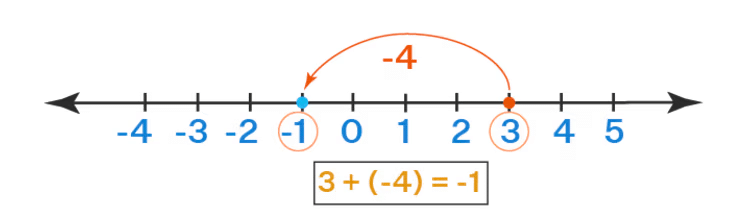

प्रश्न 24: निम्नलिखित में सही प्रतीक >, =, < डालें:="" (3="" अंक)="" (i)="" (–7)="" _________="" (2)="" (ii)="" 7="" _________="" (–12)="" (iii)="" 0="" _________="" />
उत्तर: (i) < (ii)="" /> (iii) >
प्रश्न 25: निम्नलिखित भिन्नों के सेट को अवरोही क्रम में रखें: (i) 15, 35, 135, 95, 125
(ii) 37, 311, 32, 35, 310
(i) चूंकि हर एक हर (denominators) समान हैं, हम अंश (numerators) की तुलना करेंगे, तो क्रम इस प्रकार होगा:
135 > 125 > 95 > 35 > 15
(ii) जितना छोटा हर होगा, उतना ही बड़ा भिन्न होगा:
32 > 35 > 37 > 310 > 311
Q26: एक कमरे का फर्श ढकने के लिए कितनी वर्ग टाइल्स की आवश्यकता होगी, जिसकी लंबाई 4 मीटर और चौड़ाई 3 मीटर है, यदि प्रत्येक वर्ग टाइल का किनारा 0.2 मीटर है। (3 अंक)
उत्तर: कमरे के फर्श को ढकने के लिए आवश्यक वर्ग टाइल्स की संख्या जानने के लिए, पहले हमें कमरे का क्षेत्रफल वर्ग मीटर में ज्ञात करना होगा। एक आयत का क्षेत्रफल इस सूत्र द्वारा दिया जाता है:
क्षेत्रफल = लंबाई x चौड़ाई
इस मामले में, कमरे की लंबाई 4 मीटर और चौड़ाई 3 मीटर है, इसलिए कमरे का क्षेत्रफल 4 x 3 = 12 वर्ग मीटर है।
अगला, हमें एक एकल वर्ग टाइल का क्षेत्रफल ज्ञात करना होगा। एक वर्ग का क्षेत्रफल इस सूत्र द्वारा दिया जाता है:
क्षेत्रफल = किनारा x किनारा
इस मामले में, वर्ग टाइल का किनारा 0.2 मीटर है, इसलिए एक टाइल का क्षेत्रफल 0.2 x 0.2 = 0.04 वर्ग मीटर है।
कमरे के फर्श को ढकने के लिए आवश्यक टाइल्स की संख्या जानने के लिए, हम कमरे के क्षेत्रफल को एक टाइल के क्षेत्रफल से विभाजित कर सकते हैं:
12 वर्ग मीटर / 0.04 वर्ग मीटर = 300 टाइल्स
इसलिए, कमरे के फर्श को ढकने के लिए आवश्यक वर्ग टाइल्स की संख्या 300 टाइल्स है।
Q27: एक शहर में सुबह 7 बजे तापमान 5°C था। एक हीटवेव के कारण, तापमान 11 बजे 8°C बढ़ गया। बाद में, दोपहर में, जब बादल दिखाई दिए, तापमान 4°C गिर गया। रात में, यह फिर से 3°C बढ़ गया। (3 अंक) (A) 11 बजे तापमान क्या था? (B) दोपहर में तापमान क्या था? (C) रात का तापमान क्या था?
उत्तर: (A) सुबह 11 बजे: 5 + 8 = 13 तापमान 13°C था।
(B) दोपहर में: 13 - 4 = 9 तापमान 9°C था।
(C) रात में: 9 + 3 = 12 तापमान 12°C था।
प्रश्न 28: संख्या रेखा पर निम्नलिखित संख्याएँ चिह्नित करें: 5, 0, -3, -9 (5 अंक)
उत्तर:

प्रश्न 29: रीना ने अपनी शौक वर्ग समूह की आयु (वर्षों में) का डेटा एकत्र किया और उसने अपने निष्कर्ष को निम्नलिखित तरीके से रिकॉर्ड किया: (5 अंक)
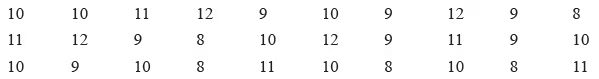
उपरोक्त डेटा को नीचे दिए गए तालिका में तल्ली मार्क्स का उपयोग करके प्रदर्शित करें:
| आयु (वर्षों में) | तल्ली मार्क्स | आवृत्ति |
|---|---|---|
| 80 | 5 | |
| 9 | ||
| 10 | ||
| 11 | ||
| 12 |
(i) वह आयु जो सबसे अधिक बार आई है, क्या है? (ii) वह आयु जो समान संख्या में आई हैं। (iii) 11 वर्ष से कम कितने बच्चे हैं? (iv) 10 वर्ष या उससे अधिक की आयु के कितने बच्चे हैं?
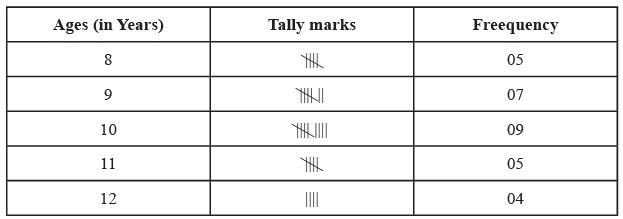
(i) वह आयु जो सबसे अधिक बार आई है, वह 10 वर्ष है। (ii) 8 वर्ष और 11 वर्ष की आयु समान संख्या में आई हैं, अर्थात् 5 बार। (iii) 11 वर्ष से कम कुल बच्चों की संख्या 5 + 7 + 9 = 21 है। (iv) 10 वर्ष और उससे अधिक की आयु के कुल बच्चों की संख्या 9 + 5 + 4 = 18 है।