NCERT Exemplar Solutions: संख्या प्रणाली | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

व्यायाम पृष्ठ: 5

प्रश्न 1 से 38 तक, चार विकल्पों में से केवल एक सही है। सही उत्तर लिखें।

प्रश्न 1: संख्या 428721 में दो 2 के स्थान मान का गुणनफल क्या है? (क) 4 (ख) 40000 (ग) 400000 (घ) 40000000

उत्तर: (ग) संख्या 428721 में दो 2 के स्थान मान का गुणनफल। इसमें दो 2 हैं। पहले 2 का स्थान मान दस का है, तो गुणनफल होगा = 2 × 10 = 20। दूसरा 2 दस हजार के स्थान पर है, तो = 2 × 10000 = 20000। इसलिए, स्थान मान का गुणनफल = 20 × 20000 = 400000।

प्रश्न 2: 3 × 10000 + 7 × 1000 + 9 × 100 + 0 × 10 + 4 का समान क्या है? (क) 3794 (ख) 37940 (ग) 37904 (घ) 379409

उत्तर: (ग) 3 × 10000 = 30000, इसका स्थान मान 30000 है। 7 × 1000 = 7000, इसका स्थान मान 7000 है। 9 × 100 = 900, इसका स्थान मान 900 है। 0 × 10 = 0। 4 = 4। इसलिए, सभी स्थान मान का योग = 30000 + 7000 + 900 + 0 + 4 = 37904।

प्रश्न 3: यदि सबसे बड़े 7-अंकीय संख्या में 1 जोड़ा जाए, तो यह क्या होगा? (क) 10 हजार (ख) 1 लाख (ग) 10 लाख (घ) 1 करोड़

उत्तर: (घ) हम जानते हैं कि सबसे बड़ी संख्या 99,99,999 है। तब, 1 जोड़ने पर 99,99,999 + 1 = 1,00,00,000 = 1 करोड़।

प्रश्न 4: संख्या 9578 का विस्तारित रूप क्या है? (क) 9 × 10000 + 5 × 1000 + 7 × 10 + 8 × 1 (ख) 9 × 1000 + 5 × 100 + 7 × 10 + 8 × 1 (ग) 9 × 1000 + 57 × 10 + 8 × 1 (घ) 9 × 100 + 5 × 100 + 7 × 10 + 8 × 1

उत्तर: (ख) दी गई संख्या 9578 पर विचार करें। 8 का स्थान मान इकाइयाँ हैं = 8 × 1। 7 का स्थान मान दस हैं = 7 × 10। 5 का स्थान मान हजार हैं = 5 × 100। 9 का स्थान मान दस हजार हैं = 9 × 1000।

प्रश्न 5: जब 85642 को निकटतम हजारों में गोल किया जाता है, तो यह (क) 85600 (ख) 85700 (ग) 85000 (घ) 86000 है।

उत्तर: (घ) जब 85642 को निकटतम हजारों में गोल किया जाता है, तो यह 86000 है।

प्रश्न 6: 5, 9, 2 और 6 अंकों से, किसी एक अंक का उपयोग दो बार करते हुए सबसे बड़ा 4-अंकीय संख्या क्या है? (क) 9652 (ख) 9562 (ग) 9659 (घ) 9965

उत्तर: (घ) 5, 9, 2 और 6 में 9 को दो बार उपयोग करते हुए, संख्या 9965 है।

प्रश्न 7: भारतीय संख्या प्रणाली में, संख्या 58695376 को कैसे लिखा जाता है? (क) 58,69,53,76 (ख) 58,695,376 (ग) 5,86,95,376 (घ) 586,95,376

उत्तर: (ग) भारतीय संख्या प्रणाली में, संख्या 58695376 को 5 करोड़, 86 लाख, 95 हजार, 376 के रूप में लिखा जाता है = 5,86,95,376।

भारत का स्थान मान चार्ट

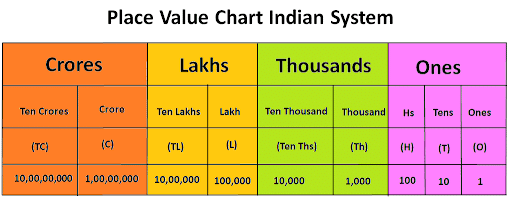
प्रश्न 8: एक मिलियन के बराबर क्या है? (क) 1 लाख (ख) 10 लाख (ग) 1 करोड़ (घ) 10 करोड़

उत्तर: (ख) एक मिलियन के बराबर 10 लाख है। 1,000,000 = 10,00,000।

प्रश्न 9: सबसे बड़ी संख्या जो निकटतम हजारों में गोल करने पर 5000 देती है, वह क्या है? (क) 5001 (ख) 5559 (ग) 5999 (घ) 5499

उत्तर: (घ) सबसे बड़ी संख्या जो निकटतम हजारों में गोल करने पर 5000 देती है, वह 5499 है।

प्रश्न 10: संख्या 6350947 में 6 का स्थान बनाए रखते हुए, अन्य अंकों को पुनर्व्यवस्थित करके प्राप्त की जाने वाली सबसे छोटी संख्या क्या है? (क) 6975430 (ख) 6043579 (ग) 6034579 (घ) 6034759

उत्तर: (ग) संख्या 6350947 में 6 का स्थान बनाए रखते हुए, अन्य अंकों को पुनर्व्यवस्थित करके प्राप्त की जाने वाली सबसे छोटी संख्या 6034579 है।

प्रश्न 11: निम्नलिखित में से कौन सा रोमन अंकों में गलत है? (क) LXXX (ख) LXX (ग) LX (घ) LLX

उत्तर: (d) जैसा कि हम जानते हैं, प्रतीक L को कभी भी दोहराया नहीं जा सकता। इसलिए, LLX गलत है।

प्रश्न 12: तीन अलग-अलग अंकों वाला सबसे बड़ा 5-आंकड़ा संख्या है (a) 98978 (b) 99897 (c) 99987 (d) 98799

उत्तर: (c) दिए गए विकल्पों में तीन संख्याएँ 9, 8 और 7 का उपयोग किया गया है। 5-आंकड़ा संख्या प्राप्त करने के लिए, हमें संख्याओं को अवरोही क्रम में व्यवस्थित करना होगा। तब, दिए गए विकल्पों में 99987 5-आंकड़ा संख्या में सबसे बड़ी है।

प्रश्न 13: तीन अलग-अलग अंकों वाली सबसे छोटी 4-आंकड़ा संख्या है (a) 1102 (b) 1012 (c) 1020 (d) 1002

उत्तर: (d) दिए गए विकल्पों में तीन संख्याएँ 0, 1 और 2 का उपयोग किया गया है। 4-आंकड़ा संख्या प्राप्त करने के लिए, हमें संख्याओं को आरोही क्रम में व्यवस्थित करना होगा। तब, दिए गए विकल्पों में 1002 4-आंकड़ा संख्या में सबसे छोटी है।

प्रश्न 14: 38 और 68 के बीच में पूर्ण संख्याओं की संख्या है (a) 31 (b) 30 (c) 29 (d) 28

उत्तर: (c) 38 और 68 के बीच में पूर्ण संख्याओं की संख्या 29 है।

प्रश्न 15: 999 का उत्तराधिकारी और पूर्ववर्ती का गुणनफल है (a) 999000 (b) 998000 (c) 989000 (d) 1998

उत्तर: (b) किसी विशेष संख्या से तुरंत पहले आने वाली संख्या को उसका पूर्ववर्ती कहा जाता है। एक पूर्ण संख्या का उत्तराधिकारी वह संख्या है जो उसमें 1 जोड़ने से प्राप्त होती है। इसलिए, 999 का उत्तराधिकारी = 999 + 1 = 1000, पूर्ववर्ती = 999 - 1 = 998। तब, 999 के उत्तराधिकारी और पूर्ववर्ती का गुणनफल = 1000 × 998 = 998000।

प्रश्न 16: एक गैर-शून्य पूर्ण संख्या और उसके उत्तराधिकारी का गुणनफल हमेशा (a) एक सम संख्या (b) एक विषम संख्या (c) एक अभाज्य संख्या (d) 3 से विभाज्य होता है

उत्तर: (a) एक गैर-शून्य पूर्ण संख्या और उसके उत्तराधिकारी का गुणनफल हमेशा एक सम संख्या होता है। उदाहरण के लिए: 4 × 5 = 20, 7 × 8 = 56।

प्रश्न 17: एक पूर्णांक को 25 में जोड़ा जाता है और वही संख्या 25 से घटाई जाती है। परिणामस्वरूप संख्याओं का योग क्या होगा? (क) 0 (ख) 25 (ग) 50 (घ) 75

उत्तर: (ग) मान लेते हैं कि संख्या x है। प्रश्न के अनुसार, संख्या जोड़ी गई है 25 में = x + 25। वही संख्या 25 से घटाई गई है = 25 – x। फिर, परिणामस्वरूप संख्याओं का योग होगा = (x + 25) + (25 – x) = x + 25 + 25 – x = 50।

प्रश्न 18: निम्नलिखित में से कौन सा सत्य नहीं है? (क) (7 + 8) + 9 = 7 + (8 + 9) (ख) (7 × 8) × 9 = 7 × (8 × 9) (ग) 7 + 8 × 9 = (7 + 8) × (7 + 9) (घ) 7 × (8 + 9) = (7 × 8) + (7 × 9)

उत्तर: (ग) बाईं ओर पर विचार करें = 7 + 8 × 9 = 7 + (8 × 9) = 7 + 72 = 79। अब, दाईं ओर पर विचार करें = (7 + 8) × (7 + 9) = 15 × 16 = 240। LHS और RHS की तुलना करने पर, LHS ≠ RHS, 79 ≠ 240।

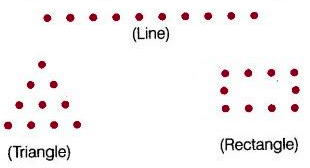
प्रश्न 19: बिंदु (.) पैटर्न का उपयोग करके, निम्नलिखित में से कौन सी संख्याएँ तीनों तरीकों में व्यवस्थित की जा सकती हैं: एक रेखा, एक त्रिकोण और एक आयत? (क) 9 (ख) 10 (ग) 11 (घ) 12

उत्तर: (ख)

प्रश्न 20: निम्नलिखित में से कौन सा कथन सत्य नहीं है? (क) जोड़ और गुणा दोनों पूर्ण संख्याओं के लिए संघटक हैं। (ख) शून्य गुणा के लिए पहचान है। (ग) जोड़ और गुणा दोनों पूर्ण संख्याओं के लिए साम्य हैं। (घ) गुणा जोड़ पर वितरक है।

उत्तर: (ख)

प्रश्न 21: निम्नलिखित में से कौन सा कथन सत्य नहीं है? (क) 0 + 0 = 0 (ख) 0 – 0 = 0 (ग) 0 × 0 = 0 (घ) 0 ÷ 0 = 0

उत्तर: (घ) शून्य को शून्य से विभाजित करना परिभाषित नहीं है।

प्रश्न 22: 1 लाख का पूर्ववर्ती क्या है? (क) 99000 (ख) 99999 (ग) 999999 (घ) 100001

प्रश्न 22: एक विशेष संख्या से ठीक पहले आने वाली संख्या को उसका पूर्ववर्ती कहा जाता है। 1 लाख का पूर्ववर्ती = 1,00,000 - 1 = 99,999

प्रश्न 23: 1 मिलियन का उत्तरवर्ती क्या है? (क) 2 मिलियन (ख) 1000001 (ग) 100001 (घ) 10001

उत्तर: (ख) एक पूर्ण संख्या का उत्तरवर्ती वह संख्या है, जो उसमें 1 जोड़ने से प्राप्त होती है। हमें पता है कि, 1 मिलियन = 10,00,000 है। इसलिए, उत्तरवर्ती = 10,00,000 + 1 = 10,00,001

प्रश्न 24: 58 और 80 के बीच सम संख्याओं की संख्या कितनी है? (क) 10 (ख) 11 (ग) 12 (घ) 13

उत्तर: (क) 58 और 80 के बीच सम संख्याएँ हैं: 60, 62, 64, 66, 68, 70, 72, 74, 76, 78।

प्रश्न 25: 16 से 80 और 90 से 100 के बीच अभाज्य संख्याओं की संख्या का योग क्या है? (क) 20 (ख) 18 (ग) 17 (घ) 16

उत्तर: (ग) 16 से 80 के बीच अभाज्य संख्याएँ हैं: 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73 और 79। इसलिए, 16 से 80 के बीच अभाज्य संख्याओं की संख्या = 16। 90 से 100 के बीच अभाज्य संख्या = 97। इसलिए, 90 से 100 के बीच अभाज्य संख्याओं की संख्या = 1। इसलिए, 16 से 80 और 90 से 100 के बीच अभाज्य संख्याओं की संख्या का योग = 16 + 1 = 17।

प्रश्न 26: निम्नलिखित में से कौन सा कथन सत्य नहीं है? (क) दो भिन्न अभाज्य संख्याओं का HCF 1 है (ख) दो सह-प्रमुख संख्याओं का HCF 1 है (ग) दो अनुक्रमिक सम संख्याओं का HCF 2 है (घ) एक सम और एक विषम संख्या का HCF सम होता है।

उत्तर: (घ) एक सम और एक विषम संख्या का HCF विषम संख्या होती है।

प्रश्न 27: सबसे बड़े 4-अंकीय संख्या के भिन्न अभाज्य गुणांक की संख्या कितनी है? (क) 2 (ख) 3 (ग) 5 (घ) 11

उत्तर: (ख) सबसे बड़ी 4-अंकीय संख्या = 9999। 9999 के अभाज्य गुणांक = 3 × 3 × 11 × 101। इसलिए, 9999 = 3² × 11 × 101। इसलिए, भिन्न अभाज्य गुणांक हैं = 3, 11 और 101। सबसे बड़े 4-अंकीय संख्या के भिन्न अभाज्य गुणांक की संख्या = 3।

प्रश्न 28: सबसे छोटे 5-अंकों वाले संख्या के भिन्न मूल कारकों की संख्या है (क) 2 (ख) 4 (ग) 6 (घ) 8

उत्तर: (क) सबसे छोटा 5-अंकों वाला संख्या = 10000 10000 के मूल कारक = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5 इस प्रकार, 10000 = 2⁴ × 5⁴ इसलिए, भिन्न मूल कारक हैं = 2 और 5 सबसे छोटे 5-अंकों वाली संख्या के भिन्न मूल कारकों की संख्या = 2

प्रश्न 29: यदि संख्या 7254*98 22 से विभाज्य है, तो * पर अंक है (क) 1 (ख) 2 (ग) 6 (घ) 0

उत्तर: (ग) संख्या में अंकों का वैकल्पिक योग लें, बाएं से दाएं पढ़ें। यदि वह 11 से विभाज्य है, तो मूल संख्या भी विभाज्य होगी। 7 – 2 5 – 4 * – 9 8 = (5 *) दिए गए संख्या 7254 * 98 के 11 से विभाज्य होने के लिए, (5 *) भी 11 से विभाज्य होना चाहिए। इसलिए, 5 * = 11 इसलिए * = 11 – 5 = 6

प्रश्न 30: सबसे बड़ा संख्या जो हमेशा किसी भी जोड़े के लगातार विषम अंकों के योग को विभाजित करता है, है (क) 2 (ख) 4 (ग) 6 (घ) 8

उत्तर: (ख) 1 + 3 = 4 = 4/4 = 1 3 + 5 = 8 = 8/4 = 2 सबसे बड़ा संख्या जो हमेशा किसी भी जोड़े के लगातार विषम अंकों के योग को विभाजित करता है, वह है 4।

प्रश्न 31: एक संख्या 5 और 6 से विभाज्य है। यह (क) 10 (ख) 15 (ग) 30 (घ) 60 से विभाज्य नहीं हो सकता है।

उत्तर: (घ) 6 और 5 का LCM 30 है। इसलिए, 30 दिए गए विकल्पों में 10, 15 और 30 से विभाज्य है। लेकिन, 30 60 से विभाज्य नहीं है।

प्रश्न 32: 1729 के मूल कारकों का योग है (क) 13 (ख) 19 (ग) 32 (घ) 39

उत्तर: (घ) 1729 के मूल कारक = 7 × 13 × 19 इसलिए, मूल अंकों का योग = 7 + 13 + 19 = 39

प्रश्न 33: सबसे बड़ा संख्या जो हमेशा किसी विषम प्राकृतिक संख्या के पूर्ववर्ती और उत्तरवर्ती के गुणनफल को विभाजित करता है, है (क) 6 (ख) 4 (ग) 16 (घ) 8

उत्तर: (b) मान लेते हैं कि एक विषम प्राकृतिक संख्या 5 है। फिर, 5 का पूर्वज = 5 - 1 = 4
5 का उत्तरज = 5 + 1 = 6
तदनुसार, पूर्वज और उत्तरज का गुणनफल = 4 × 6 = 24
24 को 4 से विभाजित करें = 24/4 = 6
इसलिए, सबसे बड़ा संख्या जो हमेशा एक विषम प्राकृतिक संख्या के पूर्वज और उत्तरज के गुणनफल को विभाजित करती है, वह 4 है।

प्रश्न 34: 75, 60, 105 के सामान्य प्रमुख गुणांक की संख्या (a) 2 (b) 3 (c) 4 (d) 5

उत्तर: (a) 75 के प्रमुख गुणांक = 3 × 5 × 5
60 के प्रमुख गुणांक = 2 × 2 × 3 × 5
105 के प्रमुख गुणांक = 3 × 5 × 7
तो, दिए गए तीन संख्याओं में सामान्य प्रमुख गुणांक 3 और 5 हैं। इसलिए, 75, 60, 105 के सामान्य प्रमुख गुणांक की संख्या 2 है।

प्रश्न 35: निम्नलिखित में से कौन-सी जोड़ी सह-प्राइम नहीं है? (a) 8, 10 (b) 11, 12 (c) 1, 3 (d) 31, 33

उत्तर: (a) सबसे पहले, दोनों संख्याएँ सम हैं। फिर, दोनों संख्याओं का सामान्य गुणांक 1 के अलावा 2 है। इसलिए, 8 और 10 सह-प्राइम नहीं हैं।

प्रश्न 36: निम्नलिखित में से कौन-सी संख्या 11 से विभाज्य है? (a) 1011011 (b) 1111111 (c) 22222222 (d) 3333333

उत्तर: (c) किसी संख्या के 11 से विभाज्य होने की जांच करने के लिए नियम है, दाईं ओर से विषम स्थानों पर अंकों का योग और सम स्थानों पर अंकों का योग का अंतर निकालें। यदि अंतर 0 है या 11 से विभाज्य है, तो संख्या 11 से विभाज्य है। तो, 2 – 2 + 2 – 2 + 2 – 2 + 2 – 2 = 0
इसलिए, 22222222 11 से विभाज्य है।

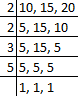
प्रश्न 37: 10, 15 और 20 का LCM (a) 30 (b) 60 (c) 90 (d) 180

उत्तर: (b) 10, 15 और 20 के गुणांक हैं, फिर, 10, 15 और 20 का LCM है 2 × 2 × 3 × 5 = 60

प्रश्न 38: दो संख्याओं का LCM 180 है। निम्नलिखित में से कौन सी संख्या संख्याओं का HCF नहीं है? (क) 45 (ख) 60 (ग) 75 (घ) 90

उत्तर: (ग) 180 के गुणांक। इसलिए, 180 के गुणांक = 2 × 2 × 3 × 3 × 5। 180 द्वारा 75 विभाजित नहीं होता। इसलिए, 75 संख्या 180 का HCF नहीं है।

प्रश्न 39: प्रश्न 39 से 98 तक यह बताएं कि दिए गए कथन सत्य (T) हैं या असत्य (F)।

प्रश्न 39: रोमन अंकन में, कोई प्रतीक तीन बार से अधिक नहीं दोहराया जाता।

सत्य। रोमन अंकों के नियम के अनुसार, कोई प्रतीक तीन बार से अधिक नहीं दोहराया जाता।

प्रश्न 40: रोमन अंकन में, यदि कोई प्रतीक दोहराया जाता है, तो उसका मान उतनी बार गुणा किया जाता है जितनी बार वह होता है।

असत्य। यदि कोई प्रतीक दोहराया जाता है, तो उसका मान उतनी बार जोड़ा जाता है जितनी बार वह होता है: जैसे II का मान 2 है, XX का मान 20 है और XXX का मान 30 है।

प्रश्न 41: 5555 = 5 × 1000 + 5 × 100 + 5 × 10 + 5 × 1

सत्य। बाईं ओर = 5555, दाईं ओर = 5 × 1000 + 5 × 100 + 5 × 10 + 5 × 1 = 5000 + 500 + 50 + 5 = 5555। बाईं ओर = दाईं ओर।

प्रश्न 42: 39746 = 3 × 10000 + 9 × 1000 + 7 × 100 + 4 × 10 + 6

सत्य। बाईं ओर = 39746, दाईं ओर = 3 × 10000 + 9 × 1000 + 7 × 100 + 4 × 10 + 6 = 30000 + 9000 + 700 + 40 + 6 = 39746। बाईं ओर = दाईं ओर।

प्रश्न 43: 82546 = 8 × 1000 + 2 × 1000 + 5 × 100 + 4 × 10 + 6

असत्य। बाईं ओर = 82546, दाईं ओर = 8 × 1000 + 2 × 1000 + 5 × 100 + 4 × 10 + 6 = 8000 + 2000 + 500 + 40 + 6 = 10,546। बाईं ओर ≠ दाईं ओर।

प्रश्न 44: 532235 = 5 × 100000 + 3 × 10000 + 2 × 1000 + 2 × 100 + 3 × 10 + 5

सत्य। बाईं ओर = 532235, दाईं ओर = 5 × 100000 + 3 × 10000 + 2 × 1000 + 2 × 100 + 3 × 10 + 5 = 5,00,000 + 30,000 + 2000 + 200 + 30 + 5 = 5,32,235। बाईं ओर = दाईं ओर।

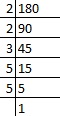
Q45: XXIX = 31

गलत। जहां, X = 10 IX = 9 तो, XXIX = 10 + 10 + 9 = 29

Q46: LXXIV = 74

सही। जहां, L = 50 X = 10 IV = 4 तो, LXXIV = 50 + 10 + 10 + 4 = 74

Q47: संख्या LIV, LVI से बड़ी है।

गलत। जहां, L = 50 IV = 4 VI = 6 तो, LIV = 50 + 4 = 54 LVI = 50 + 6 इसलिए, 54 < 56="" अतः,="" liv="" />< />

Q48: संख्याएं 4578, 4587, 5478, 5487 अवरोही क्रम में हैं।

गलत। प्रश्न में, संख्याओं का क्रम आरोही है। दी गई संख्याओं का अवरोही क्रम = 5487, 5478, 4587, 4578।

Q49: संख्या 85764 को निकटतम सैकड़ों में गोल करके 85700 लिखा जाएगा।

गलत। संख्या 85764 को निकटतम सैकड़ों में गोल करके 85800 लिखा जाएगा।

Q50: 7826 और 12469 का अनुमानित योग, सैकड़ों में गोल करके 20,000 है।

सही। संख्या 7826 को निकटतम सैकड़ों में गोल करके 7800 लिखा जाएगा। संख्या 12469 को निकटतम सैकड़ों में गोल करके 12500 लिखा जाएगा। इसलिए, गोल करने के बाद संख्याओं का योग = 7800 + 12500 = 20,300। अतः, 20,300 20,000 के निकट है।

Q51: 5, 3, 4, 7, 0, 8 अंकों का उपयोग करके केवल एक बार बना सबसे बड़ा छह अंकों का टेलीफोन नंबर 875403 है।

गलत। 5, 3, 4, 7, 0, 8 अंकों का उपयोग करके केवल एक बार बना सबसे बड़ा छह अंकों का टेलीफोन नंबर 875430 है।

Q52: संख्या 81652318 को इस प्रकार पढ़ा जाएगा: अठारह करोड़ सोलह लाख बत्तीस हजार तीन सौ अठारह।

गलत। दी गई संख्या 8,16,52,318 को इस प्रकार पढ़ा जाएगा: आठ करोड़ सोलह लाख बत्तीस हजार तीन सौ अठारह।

प्रश्न 53: 6, 7, 0, 9 अंकों का उपयोग करके बनाये जाने वाला सबसे बड़ा 4-अंक का संख्या, जिसमें प्रत्येक अंक केवल एक बार प्रयोग किया गया है, 9760 है।

प्रश्न 54: किलो, मिली और सेंटी में सबसे छोटा सेंटी है।

गलत। किलो, मिली और सेंटी में सबसे छोटा मिली है।

प्रश्न 55: एक अंकीय संख्या का उत्तराधिकारी हमेशा एक अंकीय संख्या होता है।

गलत। एक पूर्ण संख्या का उत्तराधिकारी वह संख्या है जो उसमें 1 जोड़ने पर प्राप्त होती है। उदाहरण: - संख्या 9 को लें, यह एक अंकीय संख्या है, तो इसका उत्तराधिकारी = 9 + 1 = 10।

प्रश्न 56: 3-अंक की संख्या का उत्तराधिकारी हमेशा 3-अंक की संख्या होता है।

गलत। एक पूर्ण संख्या का उत्तराधिकारी वह संख्या है जो उसमें 1 जोड़ने पर प्राप्त होती है। उदाहरण: - 3-अंक की संख्या 999 को लें, यह एक अंकीय संख्या है, तो इसका उत्तराधिकारी = 999 + 1 = 1000।

प्रश्न 57: दो-अंकी संख्या का पूर्वज हमेशा दो-अंकी संख्या होता है।

गलत। जो संख्या किसी विशेष संख्या से तुरंत पहले आती है, उसे उसका पूर्वज कहा जाता है। उदाहरण: - 2-अंकी संख्या 10 को लें, तो इसका पूर्वज = 10 - 1 = 9।

प्रश्न 58: हर पूर्ण संख्या का उसका उत्तराधिकारी होता है।

प्रश्न 59: हर पूर्ण संख्या का उसका पूर्वज होता है।

गलत। पूर्ण संख्या 0 को लें, तो इसका पूर्वज = 0 - 1 = -1 -1 एक पूर्णांक है।

प्रश्न 60: किसी भी दो प्राकृतिक संख्याओं के बीच एक प्राकृतिक संख्या होती है।

गलत। 4 और 8 दो प्राकृतिक संख्याओं को लें। तो, 4 और 8 के बीच की प्राकृतिक संख्याएँ 5, 6, 7 हैं।

प्रश्न 61: सबसे छोटी 4-अंक की संख्या सबसे बड़ी 3-अंक की संख्या का उत्तराधिकारी है।

सही। एक पूर्ण संख्या का उत्तराधिकारी वह संख्या है जो उसमें 1 जोड़ने पर प्राप्त होती है। सबसे बड़ी 3-अंक की संख्या = 999 तो, इसका उत्तराधिकारी = 999 + 1 = 1000।

Q62: दिए गए दो प्राकृतिक संख्याओं में, जो संख्या अधिक अंकों वाली होती है, वह बड़ी होती है।

सत्य। नियम के अनुसार, दिए गए दो प्राकृतिक संख्याओं में, जो संख्या अधिक अंकों वाली होती है, वह बड़ी होती है।

Q63: प्राकृतिक संख्याएँ जोड़ने में बंद हैं।

सत्य। हम जानते हैं कि, दो प्राकृतिक संख्याओं का योग हमेशा एक प्राकृतिक संख्या होती है। इसलिए, प्राकृतिक संख्याएँ जोड़ने में बंद हैं।

Q64: प्राकृतिक संख्याएँ गुणन में बंद नहीं हैं।

गलत। हम जानते हैं कि, दो प्राकृतिक संख्याओं का गुणन हमेशा एक प्राकृतिक संख्या होती है। इसलिए, प्राकृतिक संख्याएँ गुणन में बंद हैं।

Q65: प्राकृतिक संख्याएँ घटाने में बंद हैं।

गलत। दो प्राकृतिक संख्याओं का अंतर हमेशा एक प्राकृतिक संख्या नहीं होता। इसलिए, प्राकृतिक संख्याएँ घटाने में बंद नहीं हैं।

Q66: जोड़ने के लिए प्राकृतिक संख्याओं में संविधान गुण है।

सत्य। मान लीजिए ‘a’ और ‘b’ दो प्राकृतिक संख्याएँ हैं। तब प्राकृतिक संख्याओं के लिए संविधान है, a + b = b + a। दो प्राकृतिक संख्याएँ 2 और 4 लें। जहाँ, a = 2, b = 4, तब a + b = b + a, 2 + 4 = 4 + 2 = 6।

Q67: शून्य सम संख्याओं के जोड़ने के लिए पहचान है।

गलत। शून्य (0) सम संख्याओं के जोड़ने के लिए पहचान है। किसी भी सम संख्या पर विचार करें, जैसे 8। तब, 8 + 0 = 8।

Q68: एक सम संख्याओं के गुणन के लिए पहचान है।

सत्य। किसी भी सम संख्या पर विचार करें, जैसे 6। 6 × 1 = 6।

Q69: ऐसी एक सम संख्या है जो जब किसी सम संख्या में जोड़ दी जाती है, तो वही संख्या मिलती है।

सत्य। शून्य (0) एक सम संख्या है, जो जब किसी सम संख्या में जोड़ दी जाती है, तो वही संख्या मिलती है।

प्रश्न 70: एक प्राकृतिक संख्या है जिसे किसी प्राकृतिक संख्या के साथ जोड़ने पर वही संख्या प्राप्त होती है।

गलत। हम जानते हैं कि '0' एक प्राकृतिक संख्या नहीं है। इसलिए, कोई भी प्राकृतिक संख्या नहीं है जिसे किसी प्राकृतिक संख्या के साथ जोड़ने पर वही संख्या प्राप्त होती है।

प्रश्न 71: यदि एक पूर्णांक को किसी अन्य पूर्णांक द्वारा भाग दिया जाता है, जो पहले से बड़ा है, तो भागफल शून्य के बराबर नहीं होता।

सही। मानक नियम के अनुसार, यदि एक पूर्णांक को किसी अन्य पूर्णांक द्वारा भाग दिया जाता है, जो पहले से बड़ा है, तो भागफल शून्य के बराबर नहीं होता।

प्रश्न 72: कोई भी गैर-शून्य पूर्णांक जब अपने आप से भाग दिया जाता है, तो भागफल 1 होता है।

सही। किसी भी गैर-शून्य पूर्णांक को लें जैसे 5, 5 अपने आप से भाग दिया जाता है = 5/5 = 1।

प्रश्न 73: दो पूर्णांकों का गुणनफल हमेशा एक पूर्णांक नहीं होता।

गलत। दो पूर्णांकों का गुणनफल हमेशा एक पूर्णांक होता है। क्योंकि, हम जानते हैं कि पूर्णांक गुणा के अंतर्गत बंद होते हैं।

प्रश्न 74: एक पूर्णांक को 1 से बड़े किसी अन्य पूर्णांक द्वारा भाग देने पर कभी भी भागफल पहले वाले के बराबर नहीं होता।

सही। मानक नियम के अनुसार, एक पूर्णांक को 1 से बड़े किसी अन्य पूर्णांक द्वारा भाग देने पर कभी भी भागफल पहले वाले के बराबर नहीं होता।

प्रश्न 75: किसी संख्या का प्रत्येक गुणांक उस संख्या से बड़ा या उसके बराबर होता है।

सही। मानक नियम के अनुसार, किसी संख्या का प्रत्येक गुणांक उस संख्या से बड़ा या उसके बराबर होता है। उदाहरण: 2 × 1 = 2, 2 × 3 = 6।

प्रश्न 76: किसी दिए गए संख्या के गुणांकों की संख्या सीमित होती है।

गलत। किसी दिए गए संख्या के गुणांकों की संख्या अनंत होती है। क्योंकि, हम जानते हैं कि संख्याएँ अनंत होती हैं।

Q77: हर संख्या स्वयं का गुणांक है।

सत्य। हम जानते हैं कि, 1 पूर्ण संख्याओं के गुणन के लिए पहचान है। इसलिए, यदि किसी संख्या को 1 से गुणा किया जाए, तो हमें वही संख्या मिलती है। इसलिए, हर संख्या स्वयं का गुणांक है।

Q78: दो लगातार विषम संख्याओं का योग हमेशा 4 से विभाज्य होता है।

सत्य। उदाहरण के लिए, 1 + 3 = 4 = 4/4 = 1 और 11 + 13 = 24 = 24/4 = 6।

Q79: यदि एक संख्या तीन संख्याओं को ठीक से विभाजित करती है, तो उसे उनके योग को भी ठीक से विभाजित करना चाहिए।

सत्य। मानक नियम के अनुसार, यदि एक संख्या तीन संख्याओं को ठीक से विभाजित करती है, तो उसे उनके योग को भी ठीक से विभाजित करना चाहिए। मान लीजिए एक संख्या है, जैसे 2, यह 4, 6 और 8 को विभाजित करती है। तब, तीन संख्याओं का योग = 4 + 6 + 8 = 18, जो 2 से ठीक से विभाज्य है।

Q80: यदि एक संख्या तीन संख्याओं के योग को ठीक से विभाजित करती है, तो उसे उन संख्याओं को अलग-अलग भी ठीक से विभाजित करना चाहिए।

Q81: यदि एक संख्या 2 और 3 दोनों से विभाज्य है, तो वह 12 से भी विभाज्य है।

असत्य। मान लीजिए संख्या 6, यह वास्तव में 2 और 3 से विभाजित होती है, लेकिन 6 12 से विभाजित नहीं है।

Q82: एक संख्या जिसमें तीन या अधिक अंक हैं, 6 से विभाज्य होती है, यदि इसकी अंतिम दो अंकों (यानी एकक और दस) से बनी संख्या 6 से विभाज्य है।

Q83: एक संख्या जिसमें 4 या अधिक अंक हैं, 8 से विभाज्य होती है, यदि अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य है।

सत्य। विभाज्यता परीक्षण के नियम के अनुसार, एक संख्या जिसमें 4 या अधिक अंक हैं, 8 से विभाज्य होती है, यदि अंतिम तीन अंकों से बनी संख्या 8 से विभाज्य है।

Q84: यदि एक संख्या के अंकों का योग 3 से विभाज्य है, तो वह संख्या स्वयं 9 से विभाज्य होती है।

गलत. विभाज्यता परीक्षण के नियम के अनुसार, यदि किसी संख्या के अंकों का योग 9 से विभाज्य है, तो वह संख्या स्वयं भी 9 से विभाज्य होती है।

प्रश्न 85: सभी संख्याएँ जो 4 से विभाज्य हैं, वे 8 से विभाज्य नहीं हो सकतीं।

सही. संख्या 20 पर विचार करें, यह 4 से विभाज्य है लेकिन 8 से विभाज्य नहीं है।

प्रश्न 86: दो या अधिक संख्याओं का सर्वाधिक समान भाजक (HCF) उनके न्यूनतम समान गुणांक (LCM) से बड़ा होता है।

गलत. दो या अधिक संख्याओं का सर्वाधिक समान भाजक उनके न्यूनतम समान गुणांक से कम होता है।

प्रश्न 87: दो या अधिक संख्याओं का LCM उनके HCF से विभाज्य होता है।

सही. नियम के अनुसार, दो या अधिक संख्याओं का LCM उनके HCF से विभाज्य होता है।

प्रश्न 88: दो संख्याओं का LCM 28 है और उनका HCF 8 है।

गलत. प्रश्न में दिया गया है कि, दो संख्याओं का LCM 28 है और उनका HCF 8 है। लेकिन, 28 8 से ठीक से विभाजित नहीं होता।

प्रश्न 89: दो या अधिक संख्याओं का LCM उन संख्याओं में से एक हो सकता है।

सही. संख्या 2 और 4 पर विचार करें। तो, 2 और 4 का LCM 4 है।

प्रश्न 90: दो या अधिक संख्याओं का HCF उन संख्याओं में से एक हो सकता है।

प्रश्न 91: प्रत्येक पूर्ण संख्या किसी अन्य पूर्ण संख्या की उत्तराधिकारी होती है।

गलत. हमें पता है कि, 0 एक पूर्ण संख्या है। 0 किसी अन्य पूर्ण संख्या की उत्तराधिकारी नहीं है।

प्रश्न 92: दो पूर्ण संख्याओं का योग हमेशा उनके गुणनफल से कम होता है।

गलत. उदाहरण के लिए: 2 + 3 = 5 और 2 × 3 = 6। ऊपर के उदाहरण से, हम कह सकते हैं कि दो पूर्ण संख्याओं का योग हमेशा उनके गुणनफल से कम नहीं होता।

प्रश्न 93: यदि दो भिन्न पूर्ण संख्याओं का योग विषम है, तो उनका अंतर भी विषम होना चाहिए।

सत्य: दो विषम संख्याएँ 2 और 5 को विचार करें। तब, योग = 2 + 5 = 7, यह एक विषम संख्या है। अब, अंतर = 2 - 5 = 3, यह भी एक विषम संख्या है।

प्रश्न 94: कोई भी दो लगातार संख्याएँ को-प्राइम होती हैं।

सत्य: को-प्राइम संख्या वह संख्याओं का समूह है जिसमें केवल 1 उनका सामान्य गुणांक होता है, अर्थात् उनका उच्चतम सामान्य गुणांक (HCF) 1 होगा। को-प्राइम संख्याओं को सापेक्षतः प्रधान या आपस में प्रधान संख्याएँ भी कहा जाता है। यह महत्वपूर्ण है कि को-प्राइम बनाने के लिए दो संख्याएँ होनी चाहिए।

प्रश्न 95: यदि दो संख्याओं का HCF उनमें से एक संख्या है, तो उनका LCM दूसरी संख्या होगी।

प्रश्न 96: दो संख्याओं का HCF उन संख्याओं में से छोटी संख्या से छोटा होता है।

गलत: दो संख्याओं का HCF छोटी संख्या से अधिक या उसके बराबर होता है।

प्रश्न 97: दो संख्याओं का LCM बड़ी संख्या से बड़ा होता है।

गलत: दो संख्याओं का LCM बड़ी संख्या के बराबर या उससे बड़ा हो सकता है।

प्रश्न 98: दो को-प्राइम संख्याओं का LCM उन संख्याओं के गुणनफल के बराबर होता है।

प्रश्न 99: (क) 10 मिलियन = _____ करोड़।

10 मिलियन = 1 करोड़। हम जानते हैं कि, 1 मिलियन = 10 लाख। फिर, 10 मिलियन = 10 × 10 = 100 लाख = 1,00,00,000। इसलिए, 10 मिलियन = 1 करोड़।

(ख) 10 लाख = _____ मिलियन।

10 लाख = 1 मिलियन।

प्रश्न 100: (क) 1 मीटर = _____ मिलीमीटर।

1 मीटर = 1000 मिलीमीटर। हम जानते हैं कि, 1 मीटर = 100 सेंटीमीटर और 1 सेंटीमीटर = 10 मिलीमीटर। फिर, 100 सेंटीमीटर = 10 × 100 = 1000 मिलीमीटर।

(b) 1 सेंटीमीटर = _____ मिलीमीटर।

1 सेंटीमीटर = 10 मिलीमीटर।

(c) 1 किलोमीटर = _____ मिलीमीटर।

1 किलोमीटर = 10,00,000 मिलीमीटर। हमें पता है कि, 1 किमी = 1000 मीटर। 1 मीटर = 100 सेंटीमीटर। 1000 मीटर = 1000 × 100 = 1,00,000 सेंटीमीटर। 1 सेंटीमीटर = 10 मिलीमीटर। तो, 1,00,000 सेंटीमीटर = 10 × 1,00,000 = 10,00,000 मिलीमीटर।

प्रश्न 101: (a) 1 ग्राम = _____ मिलीग्राम। (b) 1 लीटर = _____ मिलीलीटर। (c) 1 किलोग्राम = _____ मिलीग्राम।

(a) 1000, (b) 1000, (c) 10,00,000

प्रश्न 102: 100 हजार = _____ लाख।

प्रश्न 103: एक व्यक्ति की ऊँचाई 1 मीटर 65 सेंटीमीटर है। उसकी ऊँचाई मिलीमीटर में _______ है।

1650: 1 मीटर 65 सेंटीमीटर = (1000 + 650) मिमी = 1650 मिमी।

प्रश्न 104: नदी 'नर्मदा' की लंबाई लगभग 1290 किलोमीटर है। इसकी लंबाई मीटर में _______ है।

1290000: 1290 किमी = (1290 × 1000) मीटर = 1290000 मीटर।

प्रश्न 105: श्रीनगर और लेह के बीच की दूरी 422 किलोमीटर है। वही दूरी मीटर में _____ है।

422000: 422 किमी = (422 × 1000) मीटर = 422000 मीटर।

प्रश्न 106: सबसे बड़े से सबसे छोटे तक संख्याओं को लिखने को _____ क्रम में व्यवस्था कहा जाता है।

प्रश्न 107: पांच विभिन्न गैर-शून्य अंकों से बनी सबसे बड़ी संख्या के अंकों का क्रम उलटने से, नई संख्या _____ अंकों की सबसे छोटी संख्या होती है।

सबसे छोटी: पांच विभिन्न गैर-शून्य अंकों से बनी सबसे बड़ी संख्या के अंकों का क्रम उलटने पर, नई संख्या इन अंकों में सबसे छोटी संख्या होती है।

प्रश्न 108: सबसे बड़े _____ अंक की संख्या में 1 जोड़ने पर, हमें दस लाख मिलता है।

6: सबसे बड़ी 6-अंक संख्या = 999999। 999999 में 1 जोड़ने पर, हमें 1000000 मिलता है।

Q109: संख्या पाँच करोड़ तेईस लाख अठहत्तर हजार चार सौ एक को भारतीय संख्या पद्धति में कोमा के साथ इस प्रकार लिखा जा सकता है _____।

5, 23, 78, 401

Q110: रोमन संख्या में, प्रतीक X को _____, M और C से ही घटाया जा सकता है।

Q111: संख्या 66 को रोमन अंकों में _____ लिखा जाता है।

एलएक्सवीआई : 66 = एलएक्सवीआई

Q112: पुणे की जनसंख्या 2001 में 2,538,473 थी। सबसे निकटतम हजार में गोल करने पर, जनसंख्या __________ थी।

2,538,000

Q113: सबसे छोटा पूरा संख्या _____ है।

0 : 0 सबसे छोटा पूरा संख्या है।

Q114: 106159 का उत्तराधिकारी _____ है।

106160 : 106159 का उत्तराधिकारी 106159 + 1, अर्थात्, 106160 है।

Q115: 100000 का पूर्वज _____ है।

99999 : 100000 का पूर्वज 100000 - 1, अर्थात्, 99999 है।

Q116: 400 का पूर्वज _____ है।

401 : 400 का पूर्वज 400 - 1, अर्थात्, 401 है।

Q117: _____ सबसे बड़े 3 अंकों की संख्या का उत्तराधिकारी है।

1000 : सबसे बड़ा 3 अंकों की संख्या = 999, 999 का उत्तराधिकारी 999 + 1, अर्थात्, 1000 है।

Q118: यदि 0 को किसी पूरे संख्या में से घटाया जाता है, तो परिणाम _____ स्वयं होता है।

Q119: 5 में समाप्त होने वाली सबसे छोटी 6 अंकों की प्राकृतिक संख्या _____ है।

100005

Q120: पूर्ण संख्याएँ _____ और _____ के अंतर्गत बंद होती हैं।

जोड़, गुणा

Q121: प्राकृतिक संख्याएँ _____ और _____ के अंतर्गत बंद होती हैं।

Q122: किसी पूरे संख्या को _____ से भाग देना परिभाषित नहीं है।

Q123: गुणा _____ के लिए पूरे संख्याओं में वितरक होता है।

प्रश्न 124: 2395 × _____ = 6195 × 2395

6195 : चूंकि, गुणा संपूर्ण संख्याओं के लिए संगणक है।

प्रश्न 125: 1001 × 2002 = 1001 × (1001 _____ )

प्रश्न 126: 10001 × 0 = _____

प्रश्न 127: 2916 × _____ = 0

प्रश्न 128: 9128 × _____ = 9128

1 : चूंकि, 1 संपूर्ण संख्याओं के लिए गुणनात्मक पहचान है।

प्रश्न 129: 125 (68 17) = (125 _____ ) 17

68 : चूंकि, जोड़ संपूर्ण संख्याओं के लिए संघटित है।

प्रश्न 130: 8925 × 1 = _____

प्रश्न 131: 19 × 12 19 = 19 × (12 _____)

1 : चूंकि, गुणा जोड़ के ऊपर वितरक है।

प्रश्न 132: 24 × 35 = 24 × 18 24 × _____

प्रश्न 133: 32 × (27 × 19) = (32 × _____ ) × 19

27 : चूंकि, गुणा संपूर्ण संख्याओं के लिए संघटित है।

प्रश्न 134: 786 × 3 786 × 7 = _____

7860 : 786 × 3 786 × 7 = 786 × (3 7) = 786 × 10 = 7860

प्रश्न 135: 24 × 25 = 24 ×

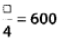
प्रश्न 136: एक संख्या अपने प्रत्येक गुणक का _____ होती है।

प्रश्न 137: _____ प्रत्येक संख्या का एक गुणक है।

प्रश्न 138: एक प्रारंभिक संख्या के गुणकों की संख्या _____ है।

प्रश्न 139: एक संख्या जिसके सभी गुणकों का योग संख्या के दो गुना के बराबर है, उसे _____ संख्या कहा जाता है।

पूर्ण

प्रश्न 140: जिन संख्याओं के दो से अधिक गुणक होते हैं, उन्हें _____ संख्याएँ कहा जाता है।

संयोजित

प्रश्न 141: 2 एकमात्र _____ संख्या है जो सम है।

प्रश्न 142: दो संख्याएँ जिनका केवल 1 एक सामान्य गुणक है, उन्हें _____ संख्याएँ कहा जाता है।

प्रश्न 143: 1 से 100 के बीच में प्राइम संख्याओं की संख्या _____ है।

25 : 1 से 100 के बीच में प्राइम संख्याएँ हैं 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97। इसलिए, 1 से 100 के बीच में 25 प्राइम संख्याएँ हैं।

Q144: यदि किसी संख्या के इकाइयों के स्थान पर _____ है, तो वह 10 से विभाज्य है।

Q145: एक संख्या 5 से विभाज्य है, यदि इसके इकाइयों के स्थान पर _____ या _____ है।

• 0, 5

Q146: यदि किसी संख्या के इकाइयों के स्थान पर 0, 2, 4, 6, या 8 में से कोई भी अंक है, तो वह _____ से विभाज्य है।

Q147: यदि किसी संख्या में अंकों का योग 3 का _____ है, तो वह संख्या 3 से विभाज्य है।

Q148: यदि किसी संख्या के अजीब स्थानों (दाएं से) में अंकों का योग और सम स्थानों (दाएं से) में अंकों का योग के बीच का अंतर 0 या _____ से विभाज्य है, तो वह संख्या 11 से विभाज्य है।

Q149: दो या अधिक दी गई संख्याओं का LCM उनके सामान्य _____ का न्यूनतम होता है।

Q150: दो या अधिक दी गई संख्याओं का HCF उनके सामान्य _____ का अधिकतम होता है।

Q151: नीचे दो कॉलम दिए गए हैं - कॉलम I और कॉलम II। कॉलम I के प्रत्येक आइटम को कॉलम II के संबंधित आइटम से मिलाएँ।

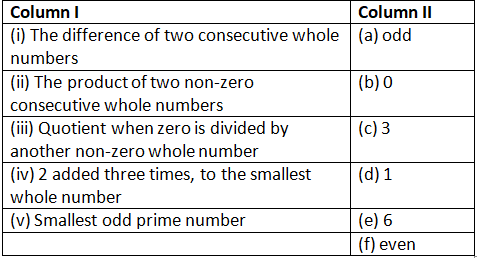
(i) ➝ (d) ; (ii) ➝ (f) ; (iii) ➝ (b) ; (iv) ➝ (e) ; (v) ➝ (c)

Q152: निम्नलिखित संख्याओं को अवरोही क्रम में व्यवस्थित करें: 8435, 4835, 13584, 5348, 25843

दी गई संख्याओं का अवरोही क्रम है, 25843, 13584, 8435, 5348, 4835

Q153: निम्नलिखित संख्याओं में से सबसे बड़ी कौन सी है? सबसे छोटी कौन सी है? 38051425, 30040700, 67205602

सबसे बड़ी संख्या है 67205602 और सबसे छोटी संख्या है 30040700।

Q154: विस्तृत रूप में लिखें: (a) 74836 (b) 574021 (c) 8907010

(a) 74836 = 7 × 10000 + 4 × 1000 + 8 × 100 + 3 × 10 + 6 × 1

(b) 574021 = 5 × 100000 + 7 × 10000 + 4 × 1000 + 0 × 100 + 2 × 10 + 1 × 1

(c) 8907010 = 8 × 1000000 + 9 × 100000 + 0 × 10000 + 7 × 1000 + 0 × 100 + 1 × 10 + 0 × 1

प्रश्न 155: 2001 की जनगणना के अनुसार, चार राज्यों की जनसंख्या निम्नलिखित है। राज्यों को उनकी जनसंख्या के अनुसार आरोही और अवरोही क्रम में व्यवस्थित करें। (क) महाराष्ट्र 96,878,627 (ख) आंध्र प्रदेश 76,210,007 (ग) बिहार 82,998,509 (घ) उत्तर प्रदेश 166,197,921

• आरोही क्रम ➝ (ख), (ग), (क), (घ)
• अवरोही क्रम ➝ (घ), (क), (ग), (ख)

प्रश्न 156: बृहस्पति का व्यास 142,800,000 मीटर है। उपयुक्त रूप से अल्पविराम डालें और अंतर्राष्ट्रीय संख्या प्रणाली के अनुसार व्यास लिखें।

बृहस्पति का व्यास 142,800,000 मीटर है।

प्रश्न 157: भारत की जनसंख्या 1961 में 439 मिलियन से बढ़कर 2001 में 1028 मिलियन हो गई है। 1961 से 2001 तक जनसंख्या में कुल वृद्धि का पता लगाएं। भारतीय संख्या प्रणाली में उपयुक्त रूप से अल्पविराम का उपयोग करते हुए जनसंख्या में वृद्धि लिखें।

1961 से 2001 तक जनसंख्या में कुल वृद्धि = 1028 मिलियन – 439 मिलियन = 589 मिलियन। भारतीय संख्या प्रणाली के अनुसार, जनसंख्या में वृद्धि = 58,90,00,000।

प्रश्न 158: पृथ्वी का व्यास 6400 किमी है और मंगल का 4300000 मीटर है। किसका व्यास बड़ा है और कितना?

पृथ्वी का व्यास = 6400 किमी = 6400 × 1000 मीटर = 6400000 मीटर। और मंगल का व्यास = 4300000 मीटर। ∴ पृथ्वी का व्यास मंगल के व्यास से (6400000 – 4300000) मीटर = 2100000 मीटर अधिक है।

प्रश्न 159: 2001 में, त्रिपुरा और मेघालय की जनसंख्या क्रमशः 3,199,203 और 2,318,822 थी। इन दोनों राज्यों की जनसंख्या शब्दों में लिखें।

त्रिपुरा की जनसंख्या = 3,199,203 अर्थात्, तीन मिलियन एक सौ निन्यानवे हजार दो सौ तीन। और मेघालय की जनसंख्या = 2,318,822 अर्थात्, दो मिलियन तीन सौ अठारह हजार आठ सौ बाईस।

प्रश्न 160: एक शहर में, मार्च 2008 में रविवार को 2,12,583 बच्चों को पोलियो की बूंदें दी गईं और अगले महीने 2,16,813 बच्चों को। दोनों महीनों में पोलियो बूंदें प्राप्त करने वाले बच्चों की संख्या का अंतर ज्ञात करें।

मार्च 2008 में पोलियो बूंदें प्राप्त करने वाले बच्चों की संख्या = 2,12,583
अप्रैल 2008 में पोलियो बूंदें प्राप्त करने वाले बच्चों की संख्या = 2,16,813
∴ दोनों महीनों में पोलियो बूंदें प्राप्त करने वाले बच्चों की संख्या का आवश्यक अंतर = 2,16,813 – 2,12,583 = 4,230

प्रश्न 161: एक व्यक्ति के पास ₹ 1000000 थे। उसने ₹ 16580 में एक रंगीन टी.वी. खरीदी, ₹ 45890 में एक मोटरसाइकिल और ₹ 870000 में एक फ्लैट खरीदा। उसके पास कितने पैसे बचे?

व्यक्ति के पास कुल राशि = ₹ 1000000
उसने रंगीन टी.वी. पर खर्च की गई राशि = ₹ 16580
उसने मोटरसाइकिल पर खर्च की गई राशि = ₹ 45890
उसने फ्लैट पर खर्च की गई राशि = ₹ 870000
∴ उसने कुल मिलाकर खर्च की गई राशि = ₹ (16580 + 45890 + 870000) = ₹ 932470
इसलिए, उसके पास बची हुई राशि = ₹ 1000000 – ₹ 932470 = ₹ 67530

प्रश्न 162: 180000 विटामिन A की गोलियों में से, 18734 गोलियाँ एक जिले के छात्रों में वितरित की गईं। शेष विटामिन गोलियों की संख्या ज्ञात करें।

कुल विटामिन A की गोलियाँ = 180000
एक जिले के छात्रों में वितरित गोलियों की संख्या = 18734
∴ शेष विटामिन गोलियों की संख्या = 180000 – 18734 = 161266

प्रश्न 163: चिन्मय के पास ₹ 610000 थे। उसने ज्योति को ₹ 87500, जावेद को ₹ 126380 और जॉन को ₹ 350000 दिए। उसके पास कितने पैसे बचे?

चिन्मय के पास कुल राशि = ₹ 610000
उसने ज्योति को दी गई राशि = ₹ 87500
उसने जावेद को दी गई राशि = ₹ 126380
उसने जॉन को दी गई राशि = ₹ 350000
चिन्मय द्वारा दी गई कुल राशि = ₹ (87500 + 126380 + 350000) = ₹ 563880
इसलिए, उसके पास बची हुई राशि = ₹ 610000 – ₹ 563880 = ₹ 46120

प्रश्न 164: सात अंकों की सबसे बड़ी संख्या और आठ अंकों की सबसे छोटी संख्या के बीच का अंतर ज्ञात करें।

आठ अंकों की सबसे छोटी संख्या = 10000000
सात अंकों की सबसे बड़ी संख्या = 9999999
आवश्यक अंतर = 10000000 – 9999999 = 1

प्रश्न 165: एक मोबाइल नंबर में दस अंक होते हैं। नंबर के पहले चार अंकों में 9, 9, 8 और 7 होते हैं। अंतिम तीन अंक 3, 5 और 5 हैं। शेष अंकों को अद्वितीय होना चाहिए और मोबाइल नंबर को सबसे बड़ा संभव नंबर बनाना चाहिए। ये अंक क्या हैं?

एक मोबाइल नंबर में 10 अंक होते हैं। यदि पहले चार अंक 9, 9, 8 और 7 हैं और अंतिम तीन अंक 3, 5 और 5 हैं। इस प्रकार, सबसे बड़े संभव नंबर के लिए, शेष अद्वितीय अंक 6, 4 और 2 हैं।

प्रश्न 166: एक मोबाइल नंबर में दस अंक होते हैं। पहले चार अंक 9, 9, 7 और 9 हैं। 8, 3, 5, 6, 0 में से केवल एक अंक को दो बार उपयोग करके सबसे छोटी मोबाइल संख्या बनाएं।

एक मोबाइल नंबर में 10 अंक होते हैं। यदि पहले चार अंक 9, 9, 7 और 9 हैं। इस प्रकार, 8, 3, 5, 6, 0 में से केवल एक अंक को दो बार उपयोग करके सबसे छोटी मोबाइल संख्या 9979003568 है।

प्रश्न 167: एक पांच अंकों की संख्या में, दसवें स्थान का अंक 4 है, इकाई स्थान का अंक दसवें स्थान के अंक का एक चौथाई है, सौवें स्थान का अंक 0 है, हजारवें स्थान का अंक इकाई स्थान के अंक का 5 गुना है और दस हजारवें स्थान का अंक दसवें स्थान के अंक का 2 गुना है। संख्या लिखें।

एक संख्या में 5 अंक होते हैं। अब, दसवें स्थान का अंक = 4, इकाई स्थान का अंक = (1/4) x 4 = 1, सौवें स्थान का अंक = 0, हजारवें स्थान का अंक = 5 × 1 = 5, दस हजारवें स्थान का अंक = 2 × 4 = 8। इसलिए, संख्या 85041 है।

प्रश्न 168: 2, 0, 4, 7, 6, 5 अंकों का उपयोग करके बनाए गए सबसे बड़े और सबसे छोटे छह अंकों वाले संख्याओं का योग ज्ञात करें।

अंक 2, 0, 4, 7, 6, 5 का उपयोग करके सबसे बड़ी संख्या = 765420, और सबसे छोटी संख्या = 204567

∴ आवश्यक योग = 765420 + 204567 = 969987

प्रश्न 169: एक फैक्ट्री में 35874 लीटर ठंडा पेय भरा हुआ है। इसमें 200 मिलीलीटर क्षमता वाली कितनी बोतलें भरी जा सकती हैं?

कंटेनर में ठंडा पेय की मात्रा = 35874 लीटर = 35874 × 1000 मिलीलीटर = 35874000 मिलीलीटर

एक बोतल की क्षमता = 200 मिलीलीटर

∴ आवश्यक बोतलों की संख्या = 35874000 ÷ 200 = 179370

इसलिए, 179370 बोतलें ठंडा पेय से भरी जा सकती हैं।

प्रश्न 170: एक नगर की जनसंख्या 450772 है। एक सर्वेक्षण में रिपोर्ट किया गया कि हर 14 व्यक्तियों में से एक निरक्षर है। नगर में कुल कितने निरक्षर व्यक्ति हैं?

नगर की कुल जनसंख्या = 450772

चूंकि, हर 14 व्यक्तियों में से एक निरक्षर है।

∴ नगर में निरक्षर व्यक्तियों की संख्या = 450772 ÷ 14 = 32198

इसलिए, नगर में 32198 व्यक्ति निरक्षर हैं।

प्रश्न 171: 80, 96, 125, 160 का LCM ज्ञात करें।

हमारे पास, 80, 96, 125 और 160 का LCM = 2 × 2 × 2 × 2 × 2 × 3 × 5 × 5 × 5 = 12000

प्रश्न 172: विभिन्न अंकों का उपयोग करके सबसे बड़े और सबसे छोटे 5-अंकीय संख्याएँ बनाएँ जिसमें 5 दसवें स्थान पर हो।

दशम स्थान पर 5 अंक का उपयोग करके, सबसे बड़ी 5-अंकीय संख्या 98756 है, और सबसे छोटी 5-अंकीय संख्या 10253 है।

प्रश्न 173: 2 किलोग्राम 300 ग्राम में कितने ग्राम जोड़ने पर यह 5 किलोग्राम 68 ग्राम होगा?

5 किलोग्राम 68 ग्राम = (5 × 1000 + 68) ग्राम = 5068 ग्राम और 2 किलोग्राम 300 ग्राम = (2 × 1000 + 300) ग्राम = 2300 ग्राम। ∴ आवश्यक ग्रामों की संख्या जो जोड़नी चाहिए = 5068 ग्राम – 2300 ग्राम = 2768 ग्राम या 2 किलोग्राम 768 ग्राम।

प्रश्न 174: एक बॉक्स में 50 पैकेट बिस्किट हैं, प्रत्येक का वजन 120 ग्राम है। एक वैन में कितने ऐसे बॉक्स लोड किए जा सकते हैं जो 900 किलोग्राम से अधिक नहीं ले जा सकती?

एक बॉक्स का कुल वजन जिसमें 50 पैकेट बिस्किट हैं, प्रत्येक का वजन 120 ग्राम = 50 × 120 ग्राम = 6000 ग्राम। वैन की क्षमता = 900 किलोग्राम = 900 × 1000 ग्राम = 900000 ग्राम। ∴ आवश्यक बॉक्सों की संख्या = 900000 ÷ 6000 = 150। इसलिए, वैन में 150 बॉक्स लोड किए जा सकते हैं।

प्रश्न 175: पांच अरब में कितने लाख होते हैं?

50000 लाख पांच अरब बनाते हैं।

प्रश्न 176: तीन करोड़ में कितने मिलियन होते हैं?

30 मिलियन तीन करोड़ बनाते हैं।

प्रश्न 177: निम्नलिखित प्रत्येक संख्या को निकटतम सौ में गोल करके अनुमान लगाएँ:

• (a) 874 गोल करके निकटतम सौ = 900, 478 गोल करके निकटतम सौ = 500। अनुमानित योग = 900 + 500 = 1400
• (b) 793 गोल करके निकटतम सौ = 800, 397 गोल करके निकटतम सौ = 400। अनुमानित योग = 800 + 400 = 1200
• (c) 11244 गोल करके निकटतम सौ = 11200, 3507 गोल करके निकटतम सौ = 3500। अनुमानित योग = 11200 + 3500 = 14700
• (d) 17677 गोल करके निकटतम सौ = 17700, 13589 गोल करके निकटतम सौ = 13600। अनुमानित योग = 17700 + 13600 = 31300

प्रश्न 178: निम्नलिखित प्रत्येक संख्या को निकटतम दस में गोल करके अनुमान लगाएँ:

• (a) 11963 – 9369
• (b) 76877 – 7783
• (c) 10732 – 4354
• (d) 78203 – 16407

(a) 11963 को निकटतम दस में गोल करने पर = 11960
9369 को निकटतम दस में गोल करने पर = 9370
अनुमानित अंतर = 11960 – 9370 = 2590

(b) 76877 को निकटतम दस में गोल करने पर = 76880
7783 को निकटतम दस में गोल करने पर = 7780
अनुमानित अंतर = 76880 – 7780 = 69100

(c) 10732 को निकटतम दस में गोल करने पर = 10730
4354 को निकटतम दस में गोल करने पर = 4350
अनुमानित अंतर = 10730 – 4350 = 6380

(d) 78203 को निकटतम दस में गोल करने पर = 78200
16407 को निकटतम दस में गोल करने पर = 16410
अनुमानित अंतर = 78200 – 16410 = 61790

प्रश्न 179: निम्नलिखित उत्पादों का अनुमान लगाएँ, प्रत्येक संख्या को निकटतम दस में गोल करके:

• (a) 87 × 32
• (b) 311 × 113
• (c) 3239 × 28
• (d) 1385 × 789

(a) 87 को निकटतम दस में गोल करने पर = 90
32 को निकटतम दस में गोल करने पर = 30
अनुमानित उत्पाद = 90 × 30 = 2700

(b) 311 को निकटतम दस में गोल करने पर = 310
113 को निकटतम दस में गोल करने पर = 110
अनुमानित उत्पाद = 310 × 110 = 34100

(c) 3239 को निकटतम दस में गोल करने पर = 3240
28 को निकटतम दस में गोल करने पर = 30
अनुमानित उत्पाद = 3240 × 30 = 97200

(d) 1385 को निकटतम दस में गोल करने पर = 1390
789 को निकटतम दस में गोल करने पर = 790
अनुमानित उत्पाद = 1390 × 790 = 1098100

प्रश्न 180: एक नगर की जनसंख्या वर्ष 1991 में 78787 थी और वर्ष 2001 में 95833 थी। प्रत्येक जनसंख्या को निकटतम सैकड़े में गोल करके जनसंख्या में वृद्धि का अनुमान लगाएँ।

78787 को निकटतम सैकड़े में गोल करने पर = 78800
95833 को निकटतम सैकड़े में गोल करने पर = 95800
अनुमानित जनसंख्या वृद्धि = 95800 – 78800 = 17000

प्रश्न 181: सामान्य नियम का उपयोग करते हुए 758 × 6784 का अनुमान लगाएँ।

758 को 800 में गोल किया जा सकता है और 6784 को 7000 में गोल किया जा सकता है। ∴ अनुमानित उत्पाद = 800 × 7000 = 5600000

प्रश्न 182: एक वस्त्र कारखाने ने एक वर्ष में 216315 शर्ट, 182736 पैंट और 58704 जैकेट का उत्पादन किया। उस वर्ष तीनों वस्तुओं का कुल उत्पादन क्या है?

• कारखाने द्वारा उत्पादित शर्ट की संख्या = 216315
• कारखाने द्वारा उत्पादित पैंट की संख्या = 182736
• कारखाने द्वारा उत्पादित जैकेट की संख्या = 58704
• कारखाने का कुल उत्पादन = 216315 + 182736 + 58704 = 457755

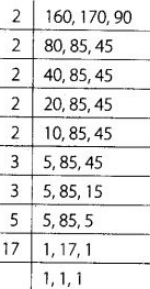
प्रश्न 183: 160, 170 और 90 का LCM ज्ञात करें।

हमारे पास है, 160, 170 और 190 का LCM = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 17 = 24480

प्रश्न 184: एक बर्तन में 13 लीटर 200 मिलीलीटर फल का रस है। इसे 60 मिलीलीटर क्षमता के कितने गिलासों में भरा जा सकता है?

एक बर्तन में फल के रस की मात्रा = 13 L 200 mL = (13 × 1000 + 200) mL = 13200 mL

एक गिलास की क्षमता = 60 mL ∴ आवश्यक गिलासों की संख्या = 13200 ÷ 60 = 220

इसलिए, फल के रस से 220 गिलास भरे जा सकते हैं।

प्रश्न 185: नीचे दिए गए चार संख्याओं का योग ज्ञात करें: (क) 32 का उत्तराधिकारी (ख) 49 का पूर्ववर्ती (ग) 56 के पूर्ववर्ती का पूर्ववर्ती (घ) 67 के उत्तराधिकारी का उत्तराधिकारी

चूंकि, 32 का उत्तराधिकारी 33 है, 49 का पूर्ववर्ती 48 है, 56 के पूर्ववर्ती का पूर्ववर्ती 54 है और 67 के उत्तराधिकारी का उत्तराधिकारी 69 है। ∴ आवश्यक योग = 33 + 48 + 54 + 69 = 204

प्रश्न 186: एक लोडिंग टेम्पो 15 किलोग्राम वजन वाले 482 बिस्किट के डिब्बे ले जा सकता है, जबकि एक वैन समान वजन के 518 डिब्बे ले जा सकती है। दोनों वाहनों द्वारा ले जाने वाले कुल वजन का पता लगाएँ।

• टेम्पो का कुल वजन = 482 × 15 kg
• वैन का कुल वजन = 518 × 15 kg

कुल वजन = (482 + 518) × 15 kg = 15000 kg

टेम्पो द्वारा ले जाने वाले कुल वजन = (482 × 15) किलोग्राम = 7230 किलोग्राम और वैन द्वारा ले जाने वाले कुल वजन = (518 × 15) किलोग्राम = 7770 किलोग्राम। इसलिए, दोनों वाहनों द्वारा ले जाने वाले कुल वजन = (7230 + 7770) किलोग्राम = 15000 किलोग्राम।

प्रश्न 187: अपनी बेटी की शादी में, लीला ने खाद्य और सजावट पर ₹ 216766, आभूषण पर ₹ 122322, फर्नीचर पर ₹ 88234 और रसोई के सामान पर ₹ 26780 खर्च किए। ऊपर बताए गए सामान पर उसने कुल कितनी राशि खर्च की?

लीला द्वारा खाद्य और सजावट पर खर्च की गई राशि = ₹ 216766
लीला द्वारा आभूषण पर खर्च की गई राशि = ₹ 122322
लीला द्वारा फर्नीचर पर खर्च की गई राशि = ₹ 88234
लीला द्वारा रसोई के सामान पर खर्च की गई राशि = ₹ 26780
∴ कुल राशि जो उसने खर्च की = ₹ (216766 + 122322 + 88234 + 26780) = ₹ 454102

प्रश्न 188: एक बक्से में 5 स्ट्रिप हैं, जिनमें प्रत्येक स्ट्रिप में 12 कैप्सूल हैं, और प्रत्येक कैप्सूल में 500mg दवा है। 32 ऐसे बक्सों में दवा का कुल वजन ग्राम में ज्ञात करें।

एक कैप्सूल में दवा की मात्रा = 500 mg
∴ 12 कैप्सूल या 1 स्ट्रिप में दवा की मात्रा = (500 × 12) mg = 6000 mg = 6 g
5 स्ट्रिप या 1 बक्से में दवा की मात्रा = (6 × 5) g = 30 g
32 बक्सों में दवा की मात्रा = (30 × 32) g = 960 g

प्रश्न 189: वह न्यूनतम संख्या ज्ञात करें जिसे 3, 4 और 5 से विभाजित करने पर प्रत्येक मामले में 2 शेष बचे।

हमें ज्ञात है कि, 3, 4 और 5 का LCM 2 × 2 × 3 × 5 = 60 है।
∴ आवश्यक संख्या 6 है, जो 3, 4 और 5 से विभाजित करने पर प्रत्येक मामले में 2 शेष छोड़ती है।

प्रश्न 190: एक व्यापारी के पास 120 लीटर एक प्रकार का तेल, 180 लीटर दूसरे प्रकार का और 240 लीटर तीसरे प्रकार का तेल है। वह तीन प्रकार के तेल को समान क्षमता की टिन में भरकर बेचना चाहता है। ऐसी टिन की सबसे बड़ी क्षमता क्या होनी चाहिए?

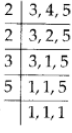
एक व्यापारी के पास 120 लीटर, 180 लीटर और 240 लीटर की मात्रा में 3 प्रकार का तेल है। क्योंकि, वह तेल को समान क्षमता की टिन में भरकर बेचना चाहता है, इसलिए ऐसी टिन की सबसे बड़ी क्षमता 120, 180 और 240 का HCF है।

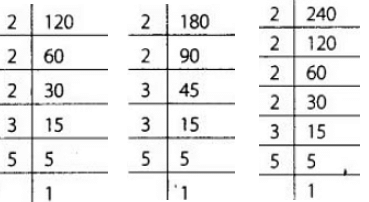
अब 120 = 2 × 2 × 2 × 3 × 5
180 = 2 × 2 × 3 × 3 × 5
240 = 2 × 2 × 2 × 2 × 3 × 4
∴ आवश्यक टिन की सबसे बड़ी क्षमता = (2 × 2 × 3 × 5) लीटर = 60 लीटर

प्रश्न 191: 1, 2, 4 और 5 के अंकों का उपयोग करते हुए एक 4-अंकीय विषम संख्या खोजें, जिसमें पहले और अंतिम अंकों को बदलने पर वह 4 से विभाज्य हो।

1, 2, 4 और 5 के अंकों का एक बार उपयोग करके, हमें एक 4-अंकीय विषम संख्या 4521 मिलती है। जब हम इसके पहले और अंतिम अंकों को बदलते हैं, तो हमें एक नया नंबर मिलता है, यानी 1524, जो 4 से विभाज्य है। इस प्रकार, आवश्यक संख्या 4521 है।

प्रश्न 192: 1, 2, 3 और 4 के अंकों का उपयोग करते हुए सबसे छोटी 4-अंकीय संख्या निर्धारित करें जो 4 से विभाज्य हो।

1, 2, 3 और 4 के अंकों का एक बार उपयोग करके, 4 से विभाज्य सबसे छोटी 4-अंकीय संख्या 1324 है।

प्रश्न 193: फातिमा तीन गांव के स्कूलों को तीन पार्सल मेल करना चाहती है। उसे पता चलता है कि पोस्टल चार्ज ₹ 20, ₹ 28 और ₹ 36 हैं। यदि वह केवल एक ही संप्रदाय के स्टाम्प खरीदना चाहती है, तो उसे तीन पार्सल मेल करने के लिए सबसे बड़ा संप्रदाय का स्टाम्प क्या खरीदना चाहिए?

तीन पार्सल भेजने के लिए पोस्टल चार्ज ₹ 20, ₹ 28 और ₹ 36 हैं। इसके अलावा, फातिमा केवल एक संप्रदाय के स्टाम्प खरीदना चाहती है। इसलिए, स्टाम्प के सबसे बड़े संप्रदाय को जानने के लिए, हम 20, 28 और 36 का HCF निकालते हैं।
अब 20 = 2 × 2 × 5
28 = 2 × 2 × 7
36 = 2 × 2 × 3 × 3
∴ 20, 28 और 36 का HCF = 2 × 2 = 4
इसलिए, ₹ 4 वह सबसे बड़ा संप्रदाय है, जिसे उसे तीन पार्सल भेजने के लिए खरीदना चाहिए।

प्रश्न 194: तीन ब्रांड A, B और C के बिस्कुट क्रमशः 12, 15 और 21 बिस्कुट के पैकेट में उपलब्ध हैं। यदि एक दुकानदार प्रत्येक ब्रांड के बिस्कुट की समान संख्या खरीदना चाहता है, तो उसे प्रत्येक ब्रांड के कितने पैकेट खरीदने चाहिए?

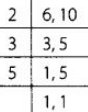
एक दुकानदार के पास तीन ब्रांड A, B और C के बिस्कुट हैं जो क्रमशः 12, 15 और 21 बिस्कुट के पैकेट में उपलब्ध हैं। दुकानदार को प्रत्येक ब्रांड के बिस्कुट की समान संख्या खरीदनी है, इसके लिए हमें 12, 15 और 21 का LCM (लघुतम गुणनखंड) निकालना होगा।

∴ 12, 15 और 21 का LCM = 2 × 2 × 3 × 5 × 7 = 420

इस प्रकार, आवश्यक पैकेट की संख्या:

• ब्रांड A = 420/12 = 35
• ब्रांड B = 420/15 = 28
• ब्रांड C = 420/21 = 20

प्रश्न 195: एक कमरे का फर्श 8 मीटर 96 सेंटीमीटर लंबा और 6 मीटर 72 सेंटीमीटर चौड़ा है। पूरे फर्श को कवर करने के लिए समान आकार के वर्ग टाइल्स की न्यूनतम संख्या ज्ञात करें।

कमरे के फर्श की लंबाई = 8 मीटर 96 सेंटीमीटर = 896 सेंटीमीटर

कमरे के फर्श की चौड़ाई = 6 मीटर 72 सेंटीमीटर = 672 सेंटीमीटर

समान आकार की वर्ग टाइल्स की न्यूनतम संख्या ज्ञात करने के लिए, हमें 896 सेंटीमीटर और 672 सेंटीमीटर का LCM निकालना होगा।

∴ 672 और 896 का LCM = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 7 = 2688

∴ टाइल्स की संख्या = 4 × 3 = 12

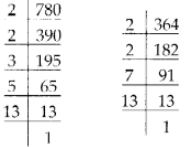
प्रश्न 196: एक स्कूल की पुस्तकालय में 780 अंग्रेजी की किताबें और 364 विज्ञान की किताबें हैं। स्कूल की पुस्तकालयाध्यक्ष, श्रीमती याकांग, इन किताबों को इस प्रकार रखना चाहती हैं कि प्रत्येक शेल्फ में प्रत्येक विषय की समान संख्या की किताबें हों। प्रत्येक शेल्फ में न्यूनतम किताबों की संख्या क्या होनी चाहिए?

अंग्रेजी की किताबों की संख्या = 780

विज्ञान की किताबों की संख्या = 364

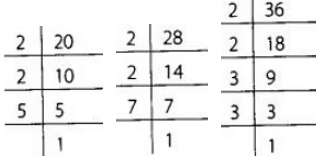
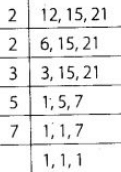
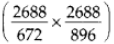
780 = 2 × 2 × 3 × 5 × 13 364 = 2 × 2 × 7 × 13 ∴ 780 और 364 का HCF = 2 × 2 × 13 = 52 इस प्रकार, प्रत्येक शेल्फ में पुस्तकों की न्यूनतम संख्या = 52

Q197: 100 फ्लैटों के एक कॉलोनी में जिनकी संख्या 1 से 100 है, एक स्कूल वैन हर छठे ब्लॉक पर रुकती है जबकि एक स्कूल बस हर दसवें ब्लॉक पर रुकती है। यदि वे कॉलोनी के प्रवेश द्वार से शुरू करें तो वे किस-किस स्थान पर रोकेंगे?

कॉलोनी में 100 ब्लॉक हैं जिनकी संख्या 1 से 100 है। एक स्कूल वैन हर छठे ब्लॉक पर रुकती है और एक स्कूल बस हर दसवें ब्लॉक पर रुकती है। हमें यह पता करना है कि वे एक ही प्रवेश द्वार से शुरू करने पर कौन से सामान्य ब्लॉक पर रुकेंगे। ∴ हमें 6 और 10 का LCM निकालना है। 6 और 10 का LCM है 2 × 3 × 5 = 30। सबसे पहले, दोनों 30वें ब्लॉक पर रुकेंगे, फिर 60वें ब्लॉक पर और अंत में 90वें ब्लॉक पर।

Q198: निम्नलिखित संख्याओं की 11 से विभाज्यता को परीक्षण करें (a) 5335 (b) 9020814

(a) हमारे पास संख्या 5335 के अजीब स्थानों (दाएं से) के अंकों का योग और सम स्थानों (दाएं से) के अंकों का योग के बीच का अंतर है (5 + 3) – (3 + 5) = 8 – 8 = 0, जो 11 से विभाज्य है। ∴ 5335 11 से विभाज्य है। (b) हमारे पास संख्या 9020814 के अजीब स्थानों (दाएं से) के अंकों का योग और सम स्थानों (दाएं से) के अंकों का योग के बीच का अंतर है (4 + 8 + 2 + 9) – (1 + 0 + 0) = 23 – 1 = 22, जो 11 से विभाज्य है। ∴ 9020814 11 से विभाज्य है।

Q199: विभाज्यता परीक्षण का उपयोग करते हुए, निम्नलिखित में से कौन सी संख्याएँ 4 से विभाज्य हैं? (a) 4096 (b) 21084 (c) 31795012

(a) हमारे पास है, 4096 चूंकि, अंतिम दो अंक 96 4 से विभाज्य हैं। ∴ 4096 4 से विभाज्य होना चाहिए। (b) हमारे पास है, 21084 चूंकि, अंतिम दो अंक 84 4 से विभाज्य हैं। ∴ 21084 4 से विभाज्य होना चाहिए। (c) हमारे पास है, 31795012 चूंकि, अंतिम दो अंक 12 4 से विभाज्य हैं। ∴ 31795012 4 से विभाज्य होना चाहिए।

Q200: विभाजन परीक्षण का उपयोग करते हुए, निम्नलिखित में से कौन से संख्या 9 से विभाज्य हैं? (क) 672 (ख) 5652

(क) हमारे पास है, 672। चूंकि 672 के सभी अंकों का योग 15 है, जो 9 से विभाज्य नहीं है। ∴ 672, 9 से विभाज्य नहीं है।

(ख) हमारे पास है, 5652। चूंकि 5652 के सभी अंकों का योग 18 है, जो 9 से विभाज्य है। ∴ 5652, 9 से विभाज्य होना चाहिए।