NCERT Exemplar Solutions: ज्यामिति | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download
व्यायाम पृष्ठ: 23
प्रश्न 1 से 16 तक, चार विकल्पों में से केवल एक सही है। सही उत्तर लिखें।
प्रश्न 1: पांच बिंदुओं से गुजरने वाली रेखाओं की संख्या, जिसमें कोई तीन बिंदु एक सीध में नहीं हैं, है (क) 10 (ख) 5 (ग) 20 (घ) 8
उत्तर: (क) प्रश्न से यह दिया गया है कि, पांच बिंदुओं से गुजरने वाली रेखाओं की संख्या। हम जानते हैं कि, एक रेखा बनाने के लिए दो बिंदुओं की आवश्यकता होती है। इसलिए, पांच बिंदुओं से गुजरने वाली रेखाओं की संख्या = 5 × 2 = 10
प्रश्न 2: एक सप्तकोण में त्रिकोणों की संख्या है (क) 21 (ख) 42 (ग) 7 (घ) 14
उत्तर: (घ) सूत्र से, त्रिकोण = n(n – 3)/2 जहां n = बहुभुज में भुजाओं की संख्या। एक सप्तकोण में 7 भुजाएँ हैं। तो, d = 7(7 – 3)/2 = 7(4)/2 = 28/2 = 14
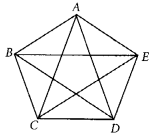
प्रश्न 3: चित्र में रेखा खंडों की संख्या है
- (क) 5
- (ख) 10
- (ग) 15
- (घ) 20

उत्तर: (ख) चित्र से, रेखा खंडों की संख्या है, AB, AC, AD, AE, BC, BD, BE, CD, CE, DE। इसलिए, दिए गए चित्र में 10 रेखा खंड हैं।
प्रश्न 4: घड़ी की घंटे और मिनट की सुइयों के बीच 9 बजे के समय में कोणों के माप हैं (क) 60º, 300º (ख) 270º, 90º (ग) 75º, 285º (घ) 30º, 330º
उत्तर: (ख) हम जानते हैं कि, घड़ी का पूरा कोण 360º है।
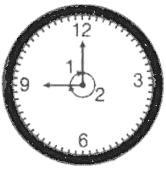
चित्र से, हम कह सकते हैं कि 2 पर कोण = (9/12) × 360º= 270º। फिर, 1 पर कोण = 360º – 270º = 90º। इसलिए, घड़ी की घंटे और मिनट की सुइयों के बीच 9 बजे के समय में कोणों के माप 270º और 90º हैं।
प्रश्न 5: यदि एक साइकिल के पहिए में 48 तंतु हैं, तो दो लगातार तंतुओं के बीच का कोण है (क) 5(1/2) (ख) 7(1/2) (ग) 2/11 (घ) 2/15
उत्तर: (b) हम जानते हैं कि, साइकिल का पहिया गोलाकार आकार में होता है। इसलिए, पहिये का कुल कोण 360º है। प्रश्न में दिया गया है कि साइकिल के पहिये में 48 स्पोक हैं। तब, दो लगातार स्पोक के बीच का कोण = 360º/48 = 7.5 = 7(1/2)
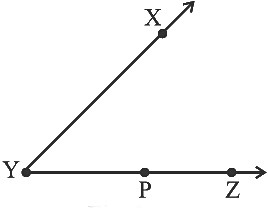
प्रश्न 6: दिए गए चित्र में, ∠XYZ को इस प्रकार नहीं लिखा जा सकता है
- (a) ∠Y
- (b) ∠ZXY
- (c) ∠ZYX
- (d) ∠XYP
प्रश्न 7: दिए गए चित्र में, यदि बिंदु A को किरण PX के साथ बिंदु B पर इस प्रकार स्थानांतरित किया जाता है कि PB = 2PA, तो ∠BPY का माप क्या होगा?
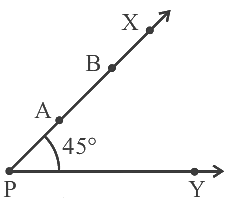
- (a) 45° से अधिक
- (b) 45°
- (c) 45° से कम
- (d) 90°
प्रश्न के अनुसार, बिंदु A को किरण PX के साथ बिंदु B पर इस प्रकार स्थानांतरित किया जाता है कि PB = 2PA। इसलिए, बिंदु 'A' को स्थानांतरित करने से बिंदु 'P' पर कोई परिवर्तन नहीं होता है। इसलिए, ∠BPY का माप 45º है।
प्रश्न 8: दिए गए चित्र में कोणों की संख्या क्या है?
- (a) 3
- (b) 4
- (c) 5
- (d) 6
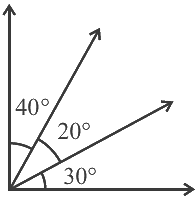
उत्तर: (d) ऊपर दिए गए चित्र से, कोण हैं, ∠POS, ∠QOS, ∠ROS, ∠POQ, ∠QOR, ∠ROS। इसलिए, बने हुए कोणों की संख्या 6 है।
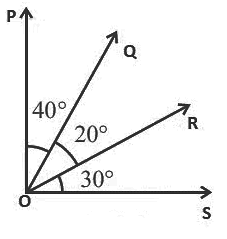
प्रश्न 9: चित्र में obtuse कोणों की संख्या क्या है?
- (a) 2
- (b) 3
- (c) 4
- (d) 5
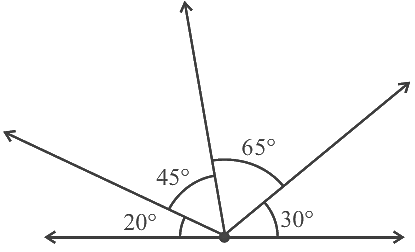
उत्तर: (c)
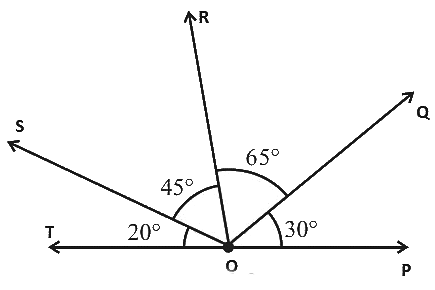
Obtuse कोण को परिभाषित किया जाता है जो 90º से अधिक और 180º से कम होता है। ऊपर दिए गए चित्र से, कोण हैं, ∠ROP = ∠ROQ ∠QOP = 65º 30º = 95º ∠SOP = ∠ROQ ∠QOP ∠SOR = 65º 30º 45º = 140º ∠SOQ = ∠SOR ∠ROQ = 45º 65º = 110º ∠TOQ = ∠TOS ∠SOR ∠ROQ = 20º 45º 65º = 130º। इसलिए, बने हुए obtuse कोणों की संख्या 4 है।
प्रश्न 10: चित्र में त्रिकोणों की संख्या क्या है?
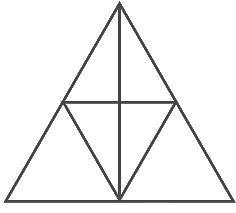
- (a) 10
- (b) 12
- (c) 13
- (d) 14
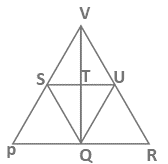
ऊपर दिए गए चित्र का अवलोकन करते हुए, कुल 13 त्रिकोण हैं। ΔPVR, ΔPSQ, ΔSQU, ΔSQT, ΔTQU, ΔQUR, ΔVSU, ΔVST, ΔVTU, ΔPQV, ΔRQV, ΔVSQ, ΔVUQ
Q11: यदि दो कोणों का योग 180° से अधिक है, तो निम्नलिखित में से कौन सा संभव नहीं है? (a) एक obtuse कोण और एक acute कोण (b) एक reflex कोण और एक acute कोण (c) दो obtuse कोण (d) दो right कोण।
उत्तर: (d) क्योंकि, दो right कोणों का योग हमेशा 180° के बराबर होता है।
Q12: यदि दो कोणों का योग एक obtuse कोण के बराबर है, तो निम्नलिखित में से कौन सा संभव नहीं है? (a) एक obtuse कोण और एक acute कोण। (b) एक right कोण और एक acute कोण। (c) दो acute कोण। (d) दो right कोण।
उत्तर: (d) क्योंकि, दो right कोणों का योग हमेशा 180° के बराबर होता है। Right angle triangle में obtuse कोण नहीं होता। Obtuse कोण को उस कोण के रूप में परिभाषित किया जाता है जो 90° से अधिक और 180° से कम होता है।
Q13: एक बहुभुज में prime संख्या में भुजाएँ हैं। इसकी भुजाओं की संख्या दो सबसे कम लगातार prime संख्याओं के योग के बराबर है। बहुभुज की diagonals की संख्या है (a) 4 (b) 5 (c) 7 (d) 10
उत्तर: (d) दो सबसे कम लगातार prime संख्याएँ हैं, 2 और 3। दो संख्याओं का योग = 2 + 3 = 5। सूत्र का उपयोग करते हुए = n(n – 3)/2 = 5(5 – 3)/2 = (5 × 2)/2 = 10/2 = 5।
Q14: दिए गए चित्र में, AB = BC और AD = BD = DC। चित्र में isosceles triangles की संख्या है
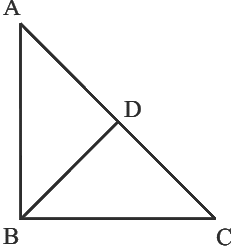
(a) 1 (b) 2 (c) 3 (d) 4
उत्तर: (c) चित्र से, ΔABC, ΔABD और ΔADC right triangles हैं।
Q15: दिए गए चित्र में, ∠BAC = 90° और AD ⊥ BC। चित्र में right triangles की संख्या है
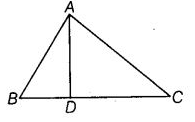
उत्तर: (c) हमारे पास है, ∠BAC = 90° और AD ⊥ BC। ∵ ∠BDA = ∠CDA = ∠BAC = 90° ∴ दिए गए चित्र में 3 right triangles बने हैं।
प्रश्न 16: दिए गए चित्र में, PQ ⊥ RQ, PQ = 5 सेंटीमीटर और QR = 5 सेंटीमीटर है। फिर ∆ PQR है
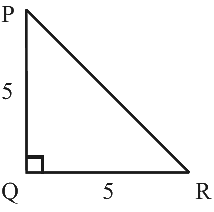
(क) एक समकोण त्रिकोण लेकिन समकोण नहीं (ख) एक समकोण समद्विभाजित त्रिकोण (ग) समद्विभाजित लेकिन समकोण नहीं (घ) न तो समद्विभाजित न ही समकोण
उत्तर: (ख) प्रश्न में दिया गया है कि, PQ ⊥ RQ, PQ = 5 सेंटीमीटर और QR = 5 सेंटीमीटर है। हमें पता है कि, समद्विभाजित त्रिकोण में दो समान भुजाएँ होती हैं। इसलिए, दिया गया ΔPQR एक समकोण समद्विभाजित त्रिकोण है।
प्रश्न 17: एक कोण जो 180° से अधिक और पूर्ण कोण से कम है, उसे _______ कहते हैं।
एक कोण जो 180° से अधिक और पूर्ण कोण से कम है, उसे रिफ्लेक्स कोण कहते हैं।
प्रश्न 18: एक षट्कोण में तिर्यक रेखाओं की संख्या ________ है।
एक षट्कोण में तिर्यक रेखाओं की संख्या 9 है। हमें पता है कि, षट्कोण में 6 भुजाएँ होती हैं। सूत्र का उपयोग करते हुए, तिर्यक रेखाओं की संख्या = n(n – 3)/2 = 6(6 – 3)/2 = 6(3)/2 = 18/2 = 9
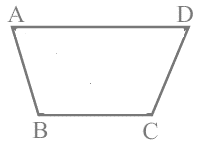
प्रश्न 19: एक समांतर चतुर्भुज की विपरीत भुजाएँ ________ हैं।
एक समांतर चतुर्भुज की विपरीत भुजाएँ समानांतर हैं।
प्रश्न 20: दिए गए चित्र में, त्रिकोण PQR के आंतरिक में स्थित बिंदु ______ हैं, बाह्य में स्थित बिंदु ______ हैं और त्रिकोण पर स्थित बिंदु ______ हैं।
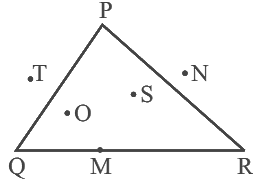
चित्र में, त्रिकोण PQR के आंतरिक में स्थित बिंदु O और S हैं, बाह्य में स्थित बिंदु N और T हैं और त्रिकोण पर स्थित बिंदु M, P, Q और R हैं।
प्रश्न 21: दिए गए चित्र में, बिंदु A, B, C, D और E एक रेखा पर स्थित हैं, इस तरह कि AB = BC = CD = DE। तब (क) AD = AB ______ (ख) AD = AC ______ (ग) AE का मध्य बिंदु ______ है (घ) CE का मध्य बिंदु ______ है (ड) AE = ______ × AB।
(क) AD = AB BD जहां, BD = BC CD (ख) AD = AC CD (ग) AE का मध्य बिंदु c है (घ) CE का मध्य बिंदु D है (ङ) AE = 4 × AB। [दी गई जानकारी]
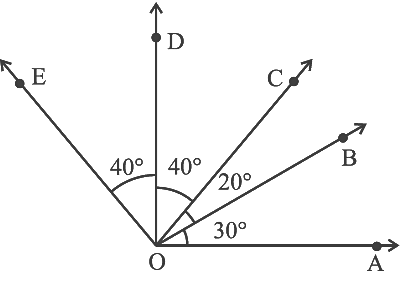
प्रश्न 22: दिए गए चित्र में। (क) ∠AOD एक ______ कोण है (ख) ∠COA एक ______ कोण है (ग) ∠AOE एक ______ कोण है
चित्र से, (क) ∠AOD एक समकोण है। यदि त्रिकोण में कोई भी कोण 90º के बराबर है, तो त्रिकोण को समकोण त्रिकोण कहा जाता है। ∠AOD = ∠AOB ∠BOC ∠COD = 30º 20º 40º
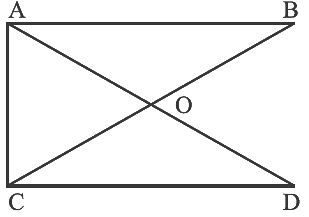
प्रश्न 23: चित्र में त्रिकोणों की संख्या ______ है। उनके नाम हैं ______________________।
चित्र में त्रिकोणों की संख्या 5 है। उनके नाम हैं ΔAOC, ΔCOD, ΔAOB, ΔACB, ΔACD।
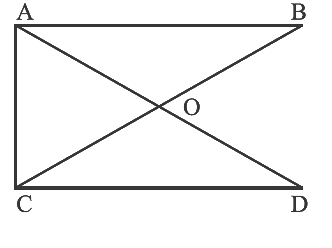
प्रश्न 24: चित्र में 180° से कम कोणों की संख्या ______ है और उनके नाम हैं।
चित्र में 180° से कम कोणों की संख्या 12 है और उनके नाम हैं ∠OAB, ∠OBA, ∠OAC, ∠OCA, ∠OCD, ∠ODC, ∠AOB, ∠AOC, ∠COD, ∠DOB, ∠BAC, ∠ACD।
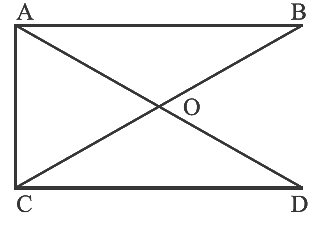
प्रश्न 25: चित्र में सीधे कोणों की संख्या ______ है।
चित्र में सीधे कोणों की संख्या चार है। कोण हैं, ∠AOD, ∠BOC, ∠COB, ∠DOA।
प्रश्न 26: सीधे कोण में सही कोणों की संख्या ______ है और पूर्ण कोण में ______ है।
सीधे कोण में सही कोणों की संख्या दो है और पूर्ण कोण में चार है। हम जानते हैं कि, सीधे कोण द्वारा निर्मित कोण = 180º और सही कोण द्वारा निर्मित कोण = 90º। इसलिए, सही कोणों की संख्या = 180º/90º = 2। हम जानते हैं कि, पूर्ण कोण = 360º। इसलिए, सही कोणों की संख्या = 360º/90º = 4।
प्रश्न 27: चित्र में अंकित दो कोणों में सामान्य बिंदुओं की संख्या ______ है।
चित्र में अंकित दो कोणों में सामान्य बिंदुओं की संख्या दो है। दिए गए चित्र से, सामान्य बिंदु P और Q हैं।

Q28: चित्र में चिह्नित दो कोणों में सामान्य बिंदुओं की संख्या ______ है।
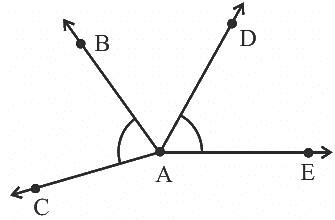
चित्र में चिह्नित दो कोणों में सामान्य बिंदुओं की संख्या एक है। दिए गए चित्र से, सामान्य बिंदु A है।
Q29: चित्र में चिह्नित दो कोणों में सामान्य बिंदुओं की संख्या ______ है।
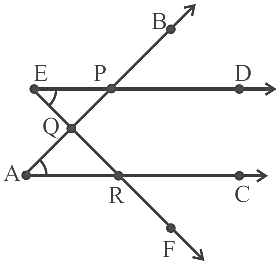
चित्र में चिह्नित दो कोणों में सामान्य बिंदुओं की संख्या तीन है। दिए गए चित्र से, सामान्य बिंदु P, Q और R हैं।
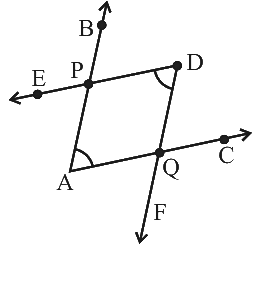
Q30: चित्र में चिह्नित दो कोणों में सामान्य बिंदुओं की संख्या ______ है।
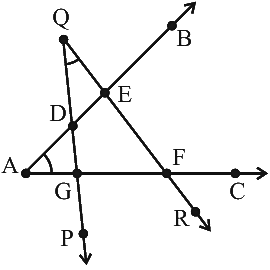
चित्र में चिह्नित दो कोणों में सामान्य बिंदुओं की संख्या चार है। दिए गए चित्र से, सामान्य बिंदु D, E, F और G हैं।
Q31: चित्र में कोण BAC और DAB के बीच सामान्य भाग ______ है।
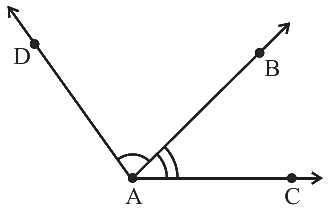
चित्र में कोण BAC और DAB के बीच सामान्य भाग रे AB है।
प्रश्न 32 से 41 तक दिए गए कथनों का सत्यापन करें (T) या असत्य (F):
Q32: एक क्षैतिज रेखा और एक ऊर्ध्वाधर रेखा हमेशा 90 डिग्री पर मिलती हैं।
सत्य.
Q33: यदि कागज पर एक कोण की भुजाएँ बढ़ाई जाती हैं, तो कोण बढ़ता है।
असत्य. यदि कागज पर एक कोण की भुजाएँ बढ़ाई या घटाई जाती हैं, तो कोण प्रभावित नहीं होता।
Q34: यदि कागज पर एक कोण की भुजाएँ घटाई जाती हैं, तो कोण घटता है।
Q35: यदि रेखा PQ || रेखा m, तो रेखा खंड PQ || m है।
सत्य. प्रश्न से, रेखा PQ || रेखा m है। फिर, उन रेखाओं के भाग भी समानांतर हैं। इसलिए, रेखा खंड PQ || m है।
Q36: दो समानांतर रेखाएँ एक दूसरे से किसी बिंदु पर मिलती हैं।
असत्य. समानांतर रेखाएँ कभी भी एक दूसरे से नहीं मिलती।
Q37: चित्र में ∠ABC और ∠CBA के माप समान हैं।
सत्य। चित्र से, दोनों ∠ABC और ∠CBA में सामान्य कोण B है।
Q38: दो रेखा खंड दो बिंदुओं पर मिल सकते हैं।
असत्य। क्योंकि, दो रेखा खंड केवल एक बिंदु पर मिलते हैं।
Q39: कई रेखाएँ दो दिए गए बिंदुओं से गुज़र सकती हैं।
असत्य। केवल एक रेखा दो दिए गए बिंदुओं से गुज़र सकती है।
Q40: केवल एक रेखा एक दिए गए बिंदु से गुज़र सकती है।
असत्य। अनंत संख्या में रेखाएँ एक दिए गए बिंदु से गुज़र सकती हैं।
Q41: दो कोणों में ठीक पाँच बिंदुओं का सामान्य होना संभव है।
असत्य। दो कोणों में या तो एक या दो बिंदुओं का सामान्य होना संभव है।
Q42: दिए गए चित्र में सभी रेखा खंडों के नाम बताएं।
रेखा खंड हैं: AB, BC, CD, DE, AC, AD, AE, BD, BE और CE।
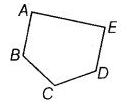
Q43: दिए गए चित्र में दिखाए गए रेखा खंडों के नाम बताएं।
रेखा खंड हैं: AB, BC, CD, DE और EA।
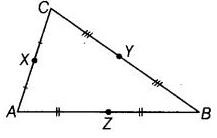
Q44: दिए गए चित्र के सभी किनारों के मध्य बिंदुओं का उल्लेख करें।
X AC का मध्य बिंदु है, Y BC का मध्य बिंदु है और Z AB का मध्य बिंदु है।
Q45: दिए गए चित्र में शीर्ष बिंदुओं और रेखा खंडों के नाम बताएं।
शीर्ष बिंदु हैं: A, B, C, D और E। रेखा खंड हैं: AB, BC, CD, DE, EA, AC और AD।
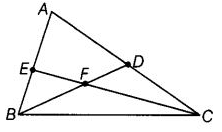
Q46: दिए गए चित्र में शामिल पंद्रह कोण (180° से कम) लिखें।
पंद्रह कोणों के नाम (180° से कम) हैं: ∠AEC, ∠ADB, ∠EAD, ∠EFD, ∠EFB, ∠DFC, ∠FBC, ∠FCB, ∠BFC, ∠ABC, ∠ACB, ∠DCF, ∠FDC, ∠EBF और ∠BEF।
Q47: दिए गए चित्र के निम्नलिखित कोणों के नाम बताएं, तीन अक्षरों का उपयोग करते हुए:
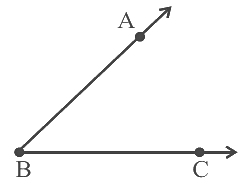
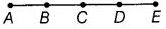
(a) ∠1 (b) ∠2 (c) ∠3 (d) ∠1 ∠2 (e) ∠2 ∠3 (f) ∠1 ∠2 ∠3 (g) ∠CBA – ∠1
(a) ∠1 = ∠CBD (b) ∠2 = ∠DBE (c) ∠3 = ∠EBA (d) ∠1 ∠2 = ∠CBD ∠DBE = ∠CBE (e) ∠2 ∠3 = ∠DBE ∠EBA = ∠DBA (f) ∠1 ∠2 ∠3 = ∠CBD ∠DBE ∠EBA = ∠CBA (g) ∠CBA – ∠1 = ∠CBA – ∠CBD = ∠DBA
प्रश्न 48: निम्नलिखित चित्रों में बिंदुओं और फिर रेखा खंडों के नाम बताइए:
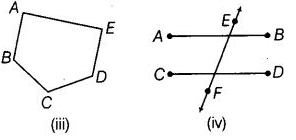
(i) बिंदुओं के नाम ➝ A, B और C। रेखा खंडों के नाम ➝ AB, BC और CA। (ii) बिंदुओं के नाम ➝ A, B, C और D। रेखा खंडों के नाम ➝ AB, BC, CD और DA। (iii) बिंदुओं के नाम ➝ A, B, C, D और E। रेखा खंडों के नाम ➝ AB, BC, CD, DE और EA। (iv) बिंदुओं के नाम ➝ A, B, C, D, E और F। रेखा खंडों के नाम ➝ AB, CD और EF।
प्रश्न 49: दिए गए चित्रों में कौन से बिंदु रेखा खंडों के मध्य बिंदु प्रतीत होते हैं? जब आप एक मध्य बिंदु खोजते हैं, तो उसके द्वारा निर्मित दो समान रेखा खंडों के नाम बताएं।
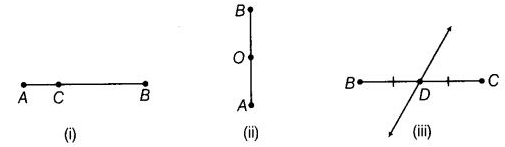
(i) दिए गए चित्र में कोई मध्य बिंदु नहीं है। (ii) दिए गए चित्र में O ZB का मध्य बिंदु है और दो समान रेखा खंडों के नाम हैं AC और OB। (iii) दिए गए चित्र में D BC का मध्य बिंदु है और दो समान रेखा खंडों के नाम हैं BD और DC।
प्रश्न 50: क्या संभव है कि (a) एक ही रेखा खंड की दो अलग-अलग लंबाई हो? (b) एक ही कोण के दो अलग-अलग माप हों?
(a) नहीं, एक ही रेखा खंड की दो अलग-अलग लंबाई होना संभव नहीं है। (b) नहीं, एक ही कोण का दो अलग-अलग माप होना संभव नहीं है।
प्रश्न 51: क्या ∠ABC और ∠CBD का माप ∠ABD के माप को बनाएगा दिए गए चित्र में?
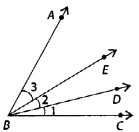
हां, ∵ ∠ABD = ∠ABC + ∠CBD ⇒ ∠ABD, ∠ABC और ∠CBD का योग है।
Q52: क्या रेखा खंड AB और रेखा खंड BC की लंबाई रेखा खंड AC की लंबाई को निर्धारित करेगी, जैसा कि दिए गए चित्र में दिखाया गया है?
हां, ∵ रेखा खंड AC की लंबाई रेखा खंड AB और BC की लंबाई का योग है।
Q53: बिना प्रोट्रैक्टर का उपयोग किए दो तीव्र कोण और एक obtuse कोण बनाएं। कोणों का माप अनुमानित करें। उन्हें प्रोट्रैक्टर की सहायता से मापें और देखें कि आपका अनुमान कितना सटीक है।
- कोणों को डिग्री में मापा जाता है। डिग्री का प्रतीक एक छोटा चक्र है। पूरा चक्र 360° (360 डिग्री) है। आधा चक्र या सीधा कोण 180° है। चौथाई चक्र या समकोण 90° है।
- प्रोट्रैक्टर का मध्य बिंदु कोण के शिखर पर रखें। कोण के एक पक्ष को प्रोट्रैक्टर की शून्य रेखा (जहां आप संख्या 0 देखते हैं) के साथ संरेखित करें। यहाँ पर पढ़ें कि दूसरी ओर संख्या पैमाने को कब पार करती है।
- 1. कोणों को मापें। 2. कोणों को मापें। प्रत्येक कोण को तीव्र या obtuse के रूप में लेबल करें। 3. ताशा ने एक तीव्र कोण मापा और 146° पाया। शिक्षक ने बताया कि उसने प्रोट्रैक्टर पर गलत संख्या का सेट पढ़ा था। 4. अपने प्रोट्रैक्टर का उपयोग करके निम्नलिखित कोणों को मापें। यदि आवश्यक हो, तो एक पैमाने की मदद से कोणों के पक्षों को लंबा करें। 5. चार बिंदु बनाएं और उन्हें इस प्रकार मिलाएं कि आप एक चतुर्भुज प्राप्त करें। अपने चतुर्भुज के सभी कोणों को मापें। फिर कोणों का योग करें।
Q54: दिए गए चित्र को देखें। एक बिंदु चिह्नित करें
(a) A जो ∠1 और ∠2 दोनों के आंतरिक में है। (b) B जो केवल ∠1 के आंतरिक में है। (c) बिंदु C ∠1 के आंतरिक में है। अब, यह बताएं कि क्या बिंदु B और C ∠2 के आंतरिक में भी हैं।
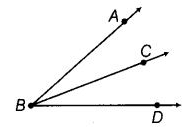
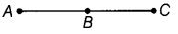
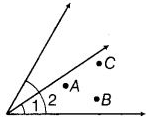
हाँ, दिए गए चित्र में यह दिखाया गया है कि बिंदु B और C भी ∠2 के अंदर स्थित हैं।
प्रश्न 55: निम्नलिखित में से गलत कथन का पता लगाएँ, यदि कोई हो: एक कोण तब बनता है जब हमारे पास (a) एक सामान्य अंत बिंदु के साथ दो किरणें (b) एक सामान्य अंत बिंदु के साथ दो रेखा खंड (c) एक किरण और एक रेखा खंड के साथ एक सामान्य अंत बिंदु है।
तीनों कथन (a), (b) और (c) गलत हैं। ∵ दो किरणों का सामान्य आरंभिक बिंदु एक कोण बनाता है।
प्रश्न 56: निम्नलिखित चित्रों में, (a) कौन सा लंबवत बिसेक्टर दिखाता है? (b) कौन सा बिसेक्टर दिखाता है? (c) केवल बिसेक्टर कौन सा दिखाता है? (d) केवल लंबवत कौन सा दिखाता है?
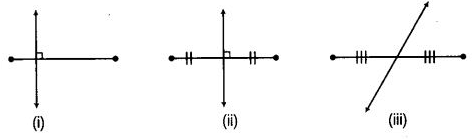
(a) चित्र (ii) लंबवत बिसेक्टर दिखाता है। (b) चित्र (ii) और (iii) बिसेक्टर दिखाते हैं। (c) चित्र (iii) केवल बिसेक्टर दिखाता है। (d) चित्र (i) केवल लंबवत दिखाता है।
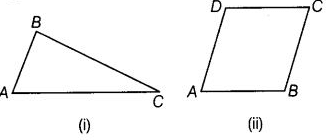
प्रश्न 57: निम्नलिखित चित्र (i) और (ii) में सामान्य क्या है?
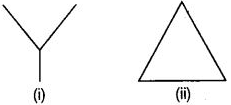
क्या चित्र (i) त्रिकोण का है? अगर नहीं, तो क्यों?
दोनों चित्र (i) और (ii) में 3 रेखा खंड हैं। नहीं, चित्र (i) त्रिकोण नहीं है क्योंकि तीन रेखा खंड एक बंद आकृति नहीं बनाते हैं।
प्रश्न 58: यदि दो किरणें एक दूसरे को काटती हैं, तो क्या उनके काटने का बिंदु उस कोण का शीर्षक होगा जिसके दो पक्ष किरणें हैं?
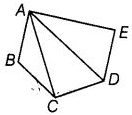
प्रश्न 59: दिए गए चित्र में,
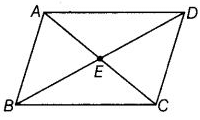
(a) कोई चार कोणों का नाम दें जो तिर्यक कोण लगते हैं। (b) कोई दो कोणों का नाम दें जो obtuse कोण लगते हैं।
(a) तिर्यक कोण: ∠ADE, ∠AEB, ∠ABE और ∠ECD। (b) obtuse कोण: ∠BCD और ∠BAD।
प्रश्न 60: दिए गए चित्र में,
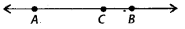
(a) क्या AC CB = AB है? (b) क्या AB AC = CB है? (c) क्या AB BC = CA है?
(a) हाँ, AC CB = AB (b) नहीं, AB – AC = CB (c) नहीं, AB – BC = CA
प्रश्न 61: दिए गए चित्र में
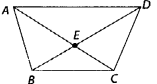
(a) AB BC क्या है? (b) AC – EC क्या है? (c) BD – BE क्या है? (d) BD – DE क्या है?
(a) AE EC = AC (b) AC – EC = AE (c) BD – BE = ED (d) BD – DE = BE
प्रश्न 62: दिए गए चित्रों के प्रत्येक भाग में सही कोणों के नाम बताएं।
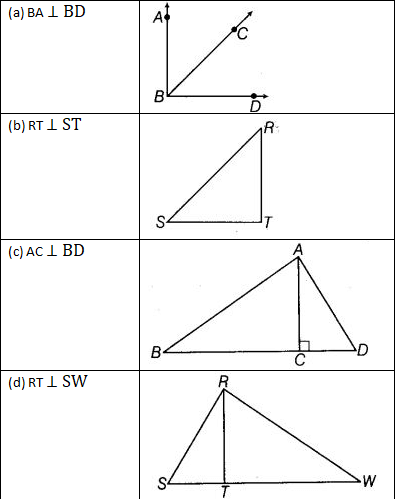
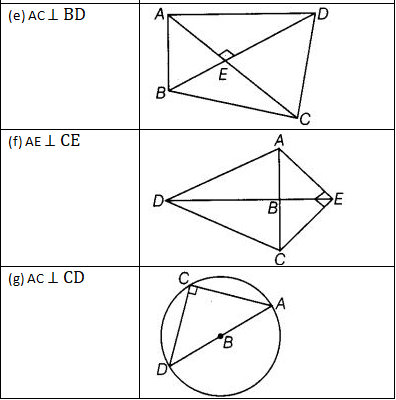
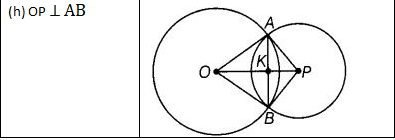
(a) ∵ BA ⊥ BD, ∴ सही कोण है ∠ABD (b) ∵ RT ⊥ ST, ∴ सही कोण है ∠RTS (c) ∵ AC ⊥ BD, ∴ सही कोण हैं ∠ACD और ∠ACB (d) ∵ RS ⊥ RW, ∴ सही कोण है ∠SRW (e) ∵ AC ⊥ BD, ∴ सही कोण हैं ∠AED, ∠AEB, ∠BEC और ∠CED (f) ∵ AE ⊥ CE, ∴ सही कोण है ∠AEC (g) ∵ AC ⊥ CD, ∴ सही कोण है ∠ACD (h) ∵ OP ⊥ AB, ∴ सही कोण हैं ∠AKO, ∠AKP, ∠BKO और ∠BKP।
प्रश्न 63: यदि (a) DB ∠ADC का बाईसेक्टर है, तो दिए गए चित्रों के प्रत्येक भाग से क्या निष्कर्ष निकाला जा सकता है?
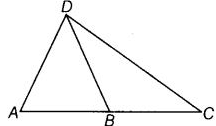
(b) BD ∠ABC को बाईसेक्ट करता है। (c) DC ∠ADB का बाईसेक्टर है, CA ⊥ DA और CB ⊥ DB
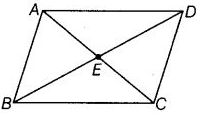
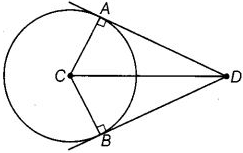
(a) ∵ DB ∠ADC का बाईसेक्टर है। ∴ ∠ADB = ∠CDB (b) ∵ BD ∠ABC को बाईसेक्ट करता है। ∴ ∠ABD = ∠CBD (c) ∵ DC ∠ADB का बाईसेक्टर है, CA ⊥ DA और CB ⊥ DB ∠ADC = ∠BDC, ∠CAD = ∠CBD = 90°
प्रश्न 64: एक कोण को त्रिभुजित कहा जाता है, यदि इसे तीन समान भागों में विभाजित किया जाए। यदि दिए गए चित्र में, ∠BAC = ∠CAD = ∠DAE, तो ∠BAE के लिए कितने त्रिभुजित हैं?
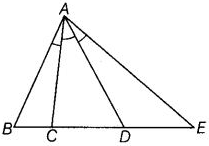
हमें दिया गया है, ∠BAC = ∠CAD = ∠DAE ∴ दो त्रिभुजित हैं, अर्थात् AC और AD।
प्रश्न 65: दिए गए चित्र में कितने बिंदु चिह्नित हैं?
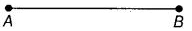
दो बिंदु A और B चिह्नित हैं।
प्रश्न 66: दिए गए चित्र में कितने रेखा खंड हैं?
केवल एक रेखा खंड, AB है।
प्रश्न 67: दिए गए चित्र में, कितने बिंदुओं को चिह्नित किया गया है? उनके नाम बताएं।

तीन बिंदु A, B और C को चिह्नित किया गया है।
प्रश्न 68: दिए गए चित्र में कितने रेखा खंड हैं? उनके नाम बताएं।

तीन रेखा खंड हैं, अर्थात् AB, BC और AC।
प्रश्न 69: दिए गए चित्र में कितने बिंदुओं को चिह्नित किया गया है? उनके नाम बताएं।

चार बिंदु A, B, C और D को चिह्नित किया गया है।
प्रश्न 70: दिए गए चित्र में कितने रेखा खंड हैं? उनके नाम बताएं।
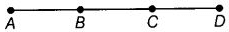
छह रेखा खंड हैं, अर्थात् AB, AC, AD, BC, BD और CD।
प्रश्न 71: दिए गए चित्र में कितने बिंदुओं को चिह्नित किया गया है? उनके नाम बताएं।
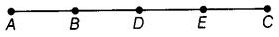
पाँच बिंदु चिह्नित किए गए हैं, अर्थात् A, B, D, E और C।
प्रश्न 72: दिए गए चित्र में कितने रेखा खंड हैं? उनके नाम बताएं।
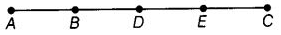
दस रेखा खंड हैं, अर्थात् AB, AD, AE, AC, BD, BE, BC, DE, DC और EC।
प्रश्न 73: दिए गए चित्र में, O वृत्त का केंद्र है।
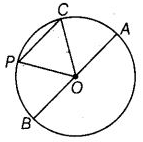
(क) वृत्त की सभी तंतुओं के नाम बताएं। (ख) वृत्त की सभी त्रिज्याओं के नाम बताएं। (ग) एक तंतु का नाम बताएं, जो वृत्त का व्यास नहीं है। (घ) क्षेत्रों OAC और OPB को छायांकित करें। (ङ) CP द्वारा बनाई गई वृत्त का छोटा खंड छायांकित करें।
(क) तंतुओं के नाम: PC और BA। (ख) त्रिज्याओं के नाम: PO, OC, OB और OA। (ग) PC एक तंतु है जो वृत्त का व्यास नहीं है। (घ) छायांकित क्षेत्र OAC और OPB इस प्रकार हैं:
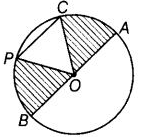
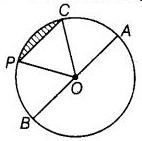
प्रश्न 74: क्या हम दो तीव्र कोण रख सकते हैं जिनका योग (क) एक तीव्र कोण है? क्यों या क्यों नहीं? (ख) एक समकोण है? क्यों या क्यों नहीं? (ग) एक अदल कोण है? क्यों या क्यों नहीं? (घ) एक सीधा कोण है? क्यों या क्यों नहीं? (ङ) एक अवतल कोण है? क्यों या क्यों नहीं?
(क) हाँ, ∵ दो तीव्र कोणों का योग एक तीव्र कोण हो सकता है। उदाहरण: 30° और 40° दो तीव्र कोण हैं और उनका योग = 30° + 40° = 70°, जो एक तीव्र कोण है। (ख) हाँ, ∵ दो तीव्र कोणों का योग समकोण हो सकता है। उदाहरण: 30° और 60° दो तीव्र कोण हैं और उनका योग = 30° + 60° = 90°, जो एक समकोण है। (ग) हाँ, ∵ दो तीव्र कोणों का योग एक अदल कोण हो सकता है। उदाहरण: 45° और 60° दो तीव्र कोण हैं और उनका योग = 45° + 60° = 105°, जो एक अदल कोण है। (घ) नहीं, ∵ दो तीव्र कोणों का योग हमेशा 180° से कम होता है। (ङ) नहीं, ∵ दो तीव्र कोणों का योग हमेशा 180° से कम होता है।

प्रश्न 75: क्या हमारे पास दो obtuse कोण हो सकते हैं जिनका योग (a) एक reflex कोण है? क्यों या क्यों नहीं? (b) एक पूर्ण कोण है? क्यों या क्यों नहीं?
(a) हाँ, क्योंकि दो obtuse कोणों का योग हमेशा 180° से अधिक होता है। उदाहरण के लिए, 135° और 100° दो obtuse कोण हैं और उनका योग = 135° + 100° = 235° है, जो 180° से अधिक है। (b) नहीं, क्योंकि दो obtuse कोणों का योग 180° से अधिक लेकिन 360° से कम होता है। ऊपर दिए गए उदाहरण में, हम देख सकते हैं कि 135° और 100° का योग, अर्थात् 235°, 180° से अधिक है लेकिन 360° से कम है।
प्रश्न 76: दिए गए चित्र में prism के (a) vertices (b) edges, और (c) faces के नाम लिखिए।
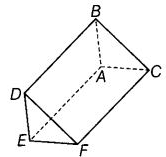
(a) Vertices: A, B, C, D, E और F। (b) Edges: AB, BC, AC, DF, FC, BD, EF, ED और AE। (c) Faces: EACF, EDBA, ABC, DEF और DBCF।
प्रश्न 77: एक sphere में कितने edges, faces और vertices होते हैं?
एक sphere में edges – 0, faces – 0 और vertices – 0 होते हैं।
प्रश्न 78: एक pentagon ABCDE की सभी diagonals को खींचिए और उनका नाम बताइए।
Pentagon ABCDE की diagonals हैं AC, AD, BE, BD और EC।