EduRev

Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8)

संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

प्रश्न 1: 615 और 963 को 6 का शेषफल छोड़ते हुए विभाजित करने वाला सबसे बड़ा संख्या ज्ञात करें।

उत्तर: हमें सबसे बड़ा संख्या ज्ञात करना है जो (615 − 6) और (963 − 6) को सही ढंग से विभाजित करता है।

अतः आवश्यक संख्या = 609 और 957 का HCF

609 और 957 को प्राथमिक गुणकों में विभाजित करते हैं:

609 = 3 × 7 × 29

957 = 3 × 11 × 29

इसलिए, 609 और 957 का HCF = 29 × 3 = 87

अतः आवश्यक सबसे बड़ा संख्या 87 है।

प्रश्न 2: 285 और 1249 को क्रमशः 9 और 7 का शेषफल छोड़ते हुए विभाजित करने वाला सबसे बड़ा संख्या ज्ञात करें।

उत्तर: हमें सबसे बड़ा संख्या ज्ञात करना है जो (285 − 9) और (1249 − 7) को सही ढंग से विभाजित करता है।

आवश्यक संख्या 276 और 1242 का HCF द्वारा दी जाएगी।

276 और 1242 को प्राथमिक गुणकों में विभाजित करते हैं:

276 = 2 × 2 × 3 × 23

1242 = 2 × 3 × 3 × 3 × 23

∴ 276 और 1242 का HCF = 2 × 3 × 23 = 138।

प्रश्न 3: सबसे बड़ा संख्या क्या है जो 626, 3127 और 15628 को क्रमशः 1, 2 और 3 का शेषफल छोड़ते हुए विभाजित करता है?

उत्तर: हमें सबसे बड़ा संख्या ज्ञात करना है जो (626 − 1), (3127 − 2), और (15628 − 3) को सही ढंग से विभाजित करता है।

आवश्यक संख्या 625, 3125 और 15625 का HCF द्वारा दी जाएगी।

625, 3125, और 15625 को प्राथमिक गुणकों में विभाजित करते हैं:

625 = 5 × 5 × 5 × 5

3125 = 5 × 5 × 5 × 5 × 5

15625 = 5 × 5 × 5 × 5 × 5 × 5

इसलिए, 625, 3125 और 15625 का HCF = 5 × 5 × 5 × 5 = 625

अतः आवश्यक सबसे बड़ा संख्या 625 है।

प्रश्न 4: एक कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 8 मीटर 25 सेंटीमीटर, 6 मीटर 75 सेंटीमीटर और 4 मीटर 50 सेंटीमीटर है। निर्धारित करें कि सबसे लंबी छड़ी जो तीनों मापों को सही ढंग से माप सके।

दी गई जानकारी:

कमरे की लंबाई = 8 मीटर 25 सेंटीमीटर = 825 सेंटीमीटर

कमरे की चौड़ाई = 6 मीटर 75 सेंटीमीटर = 675 सेंटीमीटर

कमरे की ऊँचाई = 4 मीटर 50 सेंटीमीटर = 450 सेंटीमीटर

सबसे लंबी छड़ी की लंबाई 825, 675 और 450 का HCF (अधिकतम सामान्य भाजक) द्वारा दी जाएगी।

825 का प्राइम गुणनखंडन = 3 × 5 × 5 × 11

675 का प्राइम गुणनखंडन = 3 × 3 × 3 × 5 × 5

450 का प्राइम गुणनखंडन = 2 × 3 × 3 × 5 × 5

इसलिए, 825, 675 और 450 का HCF = 3 × 5 × 5 = 75

इस प्रकार, सबसे लंबी छड़ी की आवश्यक लंबाई 75 सेंटीमीटर है।

प्रश्न 5: एक आयताकार आंगन की लंबाई 20 मीटर 16 सेंटीमीटर और चौड़ाई 15 मीटर 60 सेंटीमीटर है। इसे समान आकार के चौकोर पत्थरों से पक्का किया जाना है। ऐसे पत्थरों की न्यूनतम संख्या ज्ञात करें।

उत्तर:

आयताकार आंगन की लंबाई = 20 मीटर 16 सेंटीमीटर = 2,016 सेंटीमीटर

आयताकार आंगन की चौड़ाई = 15 मीटर 60 सेंटीमीटर = 1,560 सेंटीमीटर

आयताकार आंगन को पक्का करने के लिए उपयोग किए गए चौकोर पत्थरों की न्यूनतम भुजा = (2,016 और 1,560) का HCF

2,016 का प्राइम गुणनखंडन = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7

1,560 का प्राइम गुणनखंडन = 2 × 2 × 2 × 3 × 5 × 13

(2,016, 1,560) का HCF = 2 × 2 × 2 × 3 = 24

आयताकार आंगन को पक्का करने के लिए उपयोग किए गए चौकोर पत्थरों की न्यूनतम भुजा 24 सेंटीमीटर है।

आयताकार आंगन को पक्का करने के लिए उपयोग किए गए चौकोर पत्थरों की संख्या

== 5460

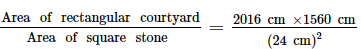
संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

इस प्रकार, आयताकार आंगन को पक्का करने के लिए उपयोग किए गए चौकोर पत्थरों की न्यूनतम संख्या 5,460 है।

प्रश्न 6: सबसे लंबे टेप का निर्धारण करें जिसे 7 मीटर, 3 मीटर 85 सेंटीमीटर और 12 मीटर 95 सेंटीमीटर की लंबाई को सटीक रूप से मापने के लिए उपयोग किया जा सकता है।

उत्तर: दी गई जानकारी:

पहली टेप की लंबाई = 7 मीटर = 700 सेंटीमीटर

दूसरी टेप की लंबाई = 3 मीटर 85 सेंटीमीटर = 385 सेंटीमीटर

तीसरी टेप की लंबाई = 12 मीटर 95 सेंटीमीटर = 1,295 सेंटीमीटर

सबसे लंबी टेप की लंबाई 700, 385, और 1,295 का एचसीएफ (HCF) होगा।

700 का प्राइम फैक्टराइजेशन = 2 × 2 × 5 × 5 × 7

385 का प्राइम फैक्टराइजेशन = 5 × 7 × 11

1,295 का प्राइम फैक्टराइजेशन = 5 × 7 × 37

∴ 700, 385, और 1,295 का एचसीएफ = 5 × 7 = 35

∴ सबसे लंबी टेप की आवश्यक लंबाई = 35 सेंटीमीटर

प्रश्न 7: 105 बकरियाँ, 140 गदहे और 175 गायों को एक नदी पार ले जाना है। वहाँ केवल एक नाव है जिसे कई बार यात्रा करनी पड़ेगी। आलसी नाविक के अपने नियम हैं। वह insists करता है कि वह हर यात्रा में एक समान संख्या में जानवर ले जाएगा और वे एक ही प्रकार के होने चाहिए। वह स्वाभाविक रूप से हर बार संभवतः सबसे बड़ी संख्या में ले जाना पसंद करेगा। क्या आप बता सकते हैं कि प्रत्येक यात्रा में कितने जानवर गए?

उत्तर: हमें जानवरों की सबसे बड़ी संख्या खोजनी है। इसलिए, हमें 105, 140, और 175 का एचसीएफ खोजना होगा।

105 का प्राइम फैक्टराइजेशन = 3 × 5 × 7

140 का प्राइम फैक्टराइजेशन = 2 × 2 × 5 × 7

175 का प्राइम फैक्टराइजेशन = 5 × 5 × 7

∴ आवश्यक एचसीएफ = 5 × 7 = 35

इसलिए, प्रत्येक यात्रा में 35 जानवर गए।

प्रश्न 8: दो ब्रांड के चॉकलेट 24 और 15 के पैक में उपलब्ध हैं। यदि मुझे दोनों प्रकार की चॉकलेट्स की समान संख्या खरीदनी है, तो मुझे प्रत्येक प्रकार के लिए न्यूनतम कितने बॉक्स खरीदने की आवश्यकता होगी?

उत्तर: मान लीजिए ब्रांड ‘A’ में एक पैकेट में 24 चॉकलेट हैं और ब्रांड ‘B’ में एक पैकेट में 15 चॉकलेट हैं।

प्रत्येक प्रकार के चॉकलेट की समान संख्या ज्ञात करने के लिए, हमें प्रत्येक पैकेट में चॉकलेट की संख्या का LCM (लघुत्तम समापवर्तक) निकालना होगा।

∴ 15 और 24 का LCM है:

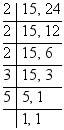
आवश्यक LCM = 2 × 2 × 2 × 3 × 5 = 120

इसलिए, प्रत्येक प्रकार के न्यूनतम 120 चॉकलेट खरीदी जानी चाहिए।

ब्रांड 'A' के पैकेट की संख्या जो खरीदनी है = 120 ÷ 24 = 5

ब्रांड 'B' के पैकेट की संख्या जो खरीदनी है = 120 ÷ 15 = 8

प्रश्न 9: एक बिक्री के दौरान, रंगीन पेंसिल 24 के पैक में और क्रेयॉन 32 के पैक में बेचे जा रहे थे। यदि आप दोनों के पूर्ण पैक और समान संख्या में पेंसिल और क्रेयॉन खरीदना चाहते हैं, तो आपको कितने पैक खरीदने होंगे?

उत्तर: आवश्यक पेंसिल और क्रेयॉन की संख्या ज्ञात करने के लिए, हमें 24 और 32 का LCM निकालना होगा।

24 का प्राथमिक गुणनखण्डन = 2 × 2 × 2 × 3

32 का प्राथमिक गुणनखण्डन = 2 × 2 × 2 × 2 × 2

∴ 24 और 32 का आवश्यक LCM = 2 × 2 × 2 × 2 × 2 × 3 = 96

इस प्रकार, पेंसिल और क्रेयॉन की संख्या जो खरीदनी है, वह 96 है, अर्थात् 96÷24=4 पैक रंगीन पेंसिल के और 96÷32 = 3 पैक क्रेयॉन के।

प्रश्न 10: निम्नलिखित भिन्नों को सबसे निम्नतम रूप में कम करें:

(i)

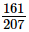
(ii)

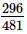
उत्तर:

(i) दिए गए भिन्न को सबसे निम्नतम रूप में कम करने के लिए, हमें इसके संख्यात्मक और हर को उनके HCF (महत्तम समापवर्तक) से भाग देना होगा।

अब, हमें 161 और 207 का HCF ज्ञात करना है।

161 का प्राथमिक गुणनखण्डन = 7 × 23

207 का प्राथमिक गुणनखण्डन = 3 × 3 × 23

∴ 161 और 207 का HCF = 23

अब, 161÷23 207÷23 = 7/9

अतः, 7/9 आवश्यक भिन्न है।

(ii) दिए गए भिन्न को न्यूनतम रूप में लाने के लिए, हमें इसके अंश और हर के गुणांक को उनके HCF से विभाजित करना होगा।

अब, हमें 296 और 481 का HCF ज्ञात करना है।

296 का अभाज्य गुणनखंडन = 2 × 2 × 2 × 37

481 का अभाज्य गुणनखंडन = 13 × 37

∴ 296 और 481 का HCF = 37

अब, 296 ÷ 37 = 8 और 481 ÷ 37 = 13

इसलिए, 8/13 आवश्यक भिन्न है।

Q.11. एक व्यापारी के पास एक प्रकार का 120 लीटर तेल, दूसरे प्रकार का 180 लीटर तेल और तीसरे प्रकार का 240 लीटर तेल है। वह तीनों प्रकार के तेल को समान क्षमता की टीनों में भरकर बेचना चाहता है। ऐसी टीन की सबसे बड़ी क्षमता क्या होनी चाहिए?

उत्तर: आवश्यक टीन की अधिकतम क्षमता तीनों तेल की मात्राओं का HCF है।

120 का अभाज्य गुणनखंडन = 2 × 2 × 2 × 3 × 5

180 का अभाज्य गुणनखंडन = 2 × 2 × 3 × 3 × 5

240 का अभाज्य गुणनखंडन = 2 × 2 × 2 × 2 × 3 × 5

∴ 120, 180, और 240 का HCF = 2 × 2 × 3 × 5 = 60

इसलिए, आवश्यक टीन की सबसे बड़ी क्षमता 60 लीटर होनी चाहिए।

The document संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) have been prepared according to the Class 6 exam syllabus. Information about RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) covers topics like and RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8).

Introduction of RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8)

In this doc you can find the meaning of RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) defined & explained in the simplest way possible. Besides explaining types of RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

study material

Summary

Important questions

ppt

MCQs

video lectures

Exam

mock tests for examination

Extra Questions

संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Free

संख्याओं के साथ खेलना (व्यायाम 2.8) RD Sharma Solutions | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Viva Questions

Objective type Questions

Previous Year Questions with Solutions

past year papers

shortcuts and tricks

Sample Paper

pdf

Semester Notes

practice quizzes

;

Additional Information about RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) for Class 6 Preparation

RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Free PDF Download

The RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) now and kickstart your journey towards success in the Class 6 exam.

Importance of RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8)

The importance of RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Notes

RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Notes on EduRev are your ultimate resource for success.

RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Class 6 Questions

The "RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) on the App

Students of Class 6 can study RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RD Sharma Solutions: संख्याओं के साथ खेलना (व्यायाम 2.8) is prepared as per the latest Class 6 syllabus.

Education Revolution