EduRev

Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1)

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

प्रश्न 1: सबसे छोटा प्राकृतिक संख्या लिखिए।

उत्तर: सबसे छोटी प्राकृतिक संख्या 1 है।

प्रश्न 2: सबसे छोटा समुचित संख्या लिखिए।

उत्तर: सबसे छोटी समुचित संख्या 0 (शून्य) है।

प्रश्न 3: यदि संभव हो, तो सबसे बड़ी प्राकृतिक संख्या लिखिए।

उत्तर: हमें पता है कि हर प्राकृतिक संख्या का एक उत्तराधिकारी होता है। इसलिए, कोई सबसे बड़ी प्राकृतिक संख्या नहीं है।

प्रश्न 4: यदि संभव हो, तो सबसे बड़ी समुचित संख्या लिखिए।

उत्तर: हमें पता है कि हर समुचित संख्या का एक उत्तराधिकारी होता है। इसलिए, कोई सबसे बड़ी समुचित संख्या नहीं है।

प्रश्न 5: क्या सभी प्राकृतिक संख्याएँ भी समुचित संख्याएँ हैं?

उत्तर: हाँ, सभी प्राकृतिक संख्याएँ समुचित संख्याएँ हैं।

प्रश्न 6: क्या सभी समुचित संख्याएँ भी प्राकृतिक संख्याएँ हैं?

उत्तर: नहीं, सभी समुचित संख्याएँ प्राकृतिक संख्याएँ नहीं हैं क्योंकि 0 एक समुचित संख्या है लेकिन प्राकृतिक संख्या नहीं है।

प्रश्न 7: निम्नलिखित समुचित संख्याओं का उत्तराधिकारी बताइए:

(i) 1000909
(ii) 2340900
(iii) 7039999

उत्तर:

दी गई संख्या | उत्तराधिकारी

(i) 1,000,909 | 1,000,909 + 1 = 1,000,910

(ii) 2,340,900 | 2,340,900 + 1 = 2,340,901

(iii) 7,039,999 | 7,039,999 + 1 = 7,040,000

प्रश्न 8: निम्नलिखित समुचित संख्याओं का पूर्वज बताइए:

(i) 10000
(ii) 807000
(iii) 7005000

उत्तर:

दी गई संख्या | पूर्वज

(i) 10,000 | 10,000 - 1 = 9,999

(ii) 807,000 | 807,000 - 1 = 806,999

(iii) 7,005,000 | 7,005,000 - 1 = 7,004,999

प्रश्न 9: निम्नलिखित संख्याओं को संख्या रेखा पर दर्शाइए:

2, 0, 3, 5, 7, 11, 15

उत्तर:

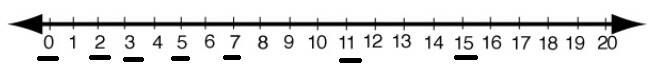
आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

प्रश्न 10: 21 और 61 के बीच कितनी समुचित संख्याएँ हैं?

उत्तर: 21 और 61 के बीच के पूर्णांक हैं 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59 और 60।

इस प्रकार, 21 और 61 के बीच कुल 39 पूर्णांक हैं।

प्रश्न 11. निम्नलिखित स्थानों को उचित प्रतीक < या > से भरें:

(i) 25 ... 205
(ii) 170 ... 107
(iii) 415 ... 514
(iv) 10001 ... 100001
(v) 2300014 ... 2300041

उत्तर: हमारे पास हैं:

(i) 25 < 205
(ii) 170 > 107
(iii) 415 < 514
(iv) 10001 < 100001
(v) 2300014 < 2300041

प्रश्न 12. निम्नलिखित संख्याओं को अवरोही क्रम में व्यवस्थित करें:

925, 786, 1100, 141, 325, 886, 0, 270

उत्तर: अवरोही क्रम में संख्याएँ:

1100, 925, 886, 786, 325, 270, 141, 0

प्रश्न 13. 6 अंकों की सबसे बड़ी संख्या और 7 अंकों की सबसे छोटी संख्या लिखें। इनमें से कौन सी संख्या बड़ी है और कितनी?

उत्तर:

सबसे बड़ी छह अंकों की संख्या = 999,999

सबसे छोटी सात अंकों की संख्या = 1,000,000

इस प्रकार, सबसे छोटी सात अंकों की संख्या सबसे बड़ी छह अंकों की संख्या से बड़ी है।

फिर,

इन दोनों संख्याओं के बीच का अंतर = 1,000,000 - 999,999 = 1

इसलिए, सबसे छोटी सात अंकों की संख्या सबसे बड़ी छह अंकों की संख्या से 1 से बड़ी है।

प्रश्न 14. 8510001 से ठीक पहले तीन लगातार पूर्णांक लिखें।

उत्तर: हमारे पास हैं:

पहली संख्या = 8,510,001 - 1 = 8,510,000

दूसरी संख्या = 8,510,000 - 1 = 8,509,999

तीसरी संख्या = 8,509,999 - 1 = 8,509,998

इसलिए, 8,510,001 से पहले के तीन लगातार पूर्णांक हैं 8,510,000, 8,509,999 और 8,509,998।

प्रश्न 15: 4,009,998 से शुरू होकर अगले तीन लगातार पूर्णांक लिखिए।

उत्तर: हमारे पास हैं:

पहला संख्या = 4,009,998 + 1 = 4,009,999
दूसरा संख्या = 4,009,999 + 1 = 4,010,000
तीसरा संख्या = 4,010,000 + 1 = 4,010,001

इसलिए, 4,009,998 से शुरू होकर अगले तीन लगातार पूर्णांक 4,009,999, 4,010,000 और 4,010,001 होंगे।

प्रश्न 16: इस कथन के समर्थन में तर्क दें कि सबसे बड़ा प्राकृतिक संख्या नहीं है।

उत्तर: हम जानते हैं कि हर प्राकृतिक संख्या का एक उत्तराधिकारी होता है। इसलिए, सबसे बड़ा प्राकृतिक संख्या मौजूद नहीं है।

प्रश्न 17: निम्नलिखित में से कौन से कथन सत्य हैं और कौन से असत्य?

(i) प्रत्येक पूर्णांक का एक उत्तराधिकारी होता है।
(ii) प्रत्येक पूर्णांक का एक पूर्ववर्ती होता है।
(iii) 0 सबसे छोटा प्राकृतिक संख्या है।
(iv) 1 सबसे छोटा पूर्णांक है।
(v) 0 हर प्राकृतिक संख्या से छोटा है।
(vi) किसी भी दो पूर्णांकों के बीच एक पूर्णांक होता है।
(vii) किसी भी दो गैर-लगातार पूर्णांकों के बीच एक पूर्णांक होता है।
(viii) सबसे छोटा 5 अंकों का संख्या सबसे बड़े 4 अंकों के संख्या का उत्तराधिकारी है।
(ix) दिए गए दो प्राकृतिक संख्याओं में, जिसकी संख्या अंकों में अधिक है, वह बड़ी है।
(x) एक दो अंकों का पूर्ववर्ती एक एक अंकों का संख्या नहीं हो सकता।
(xi) यदि a और b प्राकृतिक संख्याएँ हैं और a < b="" है,="" तो="" एक="" प्राकृतिक="" संख्या="" c="" ऐसी="" होती="" है="" कि="" a="" />< b="" />< />

(xii) यदि a और b पूर्णांक हैं और a < b="" है,="" तो="" a="" 1="" />< b="" />

(xiii) पूर्णांक 1 का पूर्वज 0 है।

(xiv) प्राकृतिक संख्या 1 का कोई पूर्वज नहीं है।

उत्तर:

(i) सत्य

हर पूर्णांक का उत्तराधिकारी 1 जोड़ने से पाया जा सकता है।

(ii) असत्य

शून्य (0) एक पूर्णांक है जिसका पूर्वज (-1) एक पूर्णांक नहीं है।

(iii) असत्य

1 सबसे छोटी प्राकृतिक संख्या है।

(iv) असत्य

शून्य (0) सबसे छोटा पूर्णांक है।

(v) सत्य

सबसे छोटी प्राकृतिक संख्या 1 है, इसलिए शून्य (0) हर प्राकृतिक संख्या से कम है।

(vi) असत्य

दो लगातार पूर्णांकों के बीच कोई पूर्णांक नहीं होता है।

(vii) सत्य

(viii) सत्य

सबसे छोटी पांच अंकों की संख्या = 10,000

सबसे बड़ी चार अंकों की संख्या = 9,999

अंतर = 10,000 - 9,999 = 1

क्योंकि अंतर 1 है, 10,000, 9,999 का उत्तराधिकारी है।

(ix) सत्य

(x) असत्य

10 एक दो अंकों की संख्या है जिसका पूर्वज 9 है, जो एक अंकों की संख्या है।

(xi) असत्य

यदि a और b लगातार प्राकृतिक संख्याएँ हैं, तो a और b के बीच में कोई प्राकृतिक संख्या c नहीं हो सकती।

(xii) सत्य

(xiii) सत्य

(xiv) सत्य

प्राकृतिक संख्या 1 का पूर्वज 0 है, जो एक प्राकृतिक संख्या नहीं है।

लक्ष्य प्रकार के प्रश्न

प्र.1. सबसे छोटी प्राकृतिक संख्या है

(क) 0

(ख) 1

(ग) -1

(घ) इनमें से कोई नहीं

उत्तर: (ख) 1

प्र.2. सबसे छोटी पूर्ण संख्या है

(क) 1

(ख) 0

उत्तर: (ख) 0

प्रश्न 3: प्राकृतिक संख्याओं में 1 का पूर्वज है

(b) 2

उत्तर: (d) इनमें से कोई नहीं

हम जानते हैं कि सबसे छोटी प्राकृतिक संख्या 1 है। इसलिए, इसका पूर्वज मौजूद नहीं है।

प्रश्न 4: पूर्ण संख्याओं में 1 का पूर्वज है

(b) -1
(c) 2

उत्तर: (a) 0

1 का पूर्वज = 1 - 1 = 0

प्रश्न 5: 1 मिलियन का पूर्वज है

(a) 9999
(b) 99999
(c) 999999
(d) 1000001

उत्तर: (c) 9,99,999

1 मिलियन = 10,00,000

1 मिलियन का पूर्वज

= 10,00,000 - 1

= 9,99,999

प्रश्न 6: 1 मिलियन का उत्तराधिकारी है

(a) 10001
(b) 100001
(c) 1000001
(d) 10000001

उत्तर: (c) 10,00,001

1 मिलियन का उत्तराधिकारी

= 10,00,000 + 1

= 10,00,001

प्रश्न 7: 99 के उत्तराधिकारी और पूर्वज का गुणनफल है

(a) 9800
(b) 9900
(c) 1099
(d) 9700

उत्तर: (a) 9800

99 का उत्तराधिकारी = 99 + 1 = 100

99 का पूर्वज = 99 − 1 = 98

इनका गुणनफल = 100 × 98 = 9800

प्रश्न 8: एक पूर्ण संख्या (शून्य के अलावा) और उसके उत्तराधिकारी का गुणनफल है

(a) एक सम संख्या
(b) एक विषम संख्या
(c) 4 द्वारा विभाज्य
(d) 3 द्वारा विभाज्य

उत्तर: (a) एक सम संख्या

उदाहरण:

पूर्ण संख्या = 1

1 का उत्तराधिकारी = 1 + 1 = 2

इनका गुणनफल = 1 × 2 = 2

इसलिए, 2 एक सम संख्या है।

प्रश्न 9: एक विषम प्राकृतिक संख्या के पूर्वज और उत्तराधिकारी का गुणनफल हमेशा विभाज्य होता है

(a) 2
(b) 4
(c) 6
(d) 8

उत्तर: (d) 8

एक विषम संख्या का पूर्ववर्ती एक सम संख्या होती है।

एक विषम संख्या का उत्तरवर्ती भी एक सम संख्या होती है।

ये दो सम संख्याएँ दो लगातार सम संख्याएँ हैं, और दो लगातार सम संख्याओं का गुणनफल हमेशा 8 से विभाज्य होता है।

प्रश्न 10: एक सम प्राकृतिक संख्या के पूर्ववर्ती और उत्तरवर्ती का गुणनफल

(a) 2 से विभाज्य
(b) 3 से विभाज्य
(d) एक विषम संख्या

उत्तर: (d) एक विषम संख्या

सम प्राकृतिक संख्या = 2

2 का पूर्ववर्ती = 2 − 1 = 1

2 का उत्तरवर्ती = 2 + 1 = 3

उनका गुणनफल = 1 × 3 = 3

इस प्रकार, गुणनफल एक विषम संख्या है।

प्रश्न 11: सबसे छोटे प्राइम संख्या का उत्तरवर्ती है

(c) 3
(d) 4

उत्तर: सबसे छोटी प्राइम संख्या 2 है।

इसलिए, 2 का उत्तरवर्ती = 2 + 1 = 3

इसलिए, सही उत्तर विकल्प (c) है।

प्रश्न 12: यदि x और y सह-प्राइम हैं, तो उनका LCM है

(b) x/y
(c) xy

उत्तर: उन संख्याओं का समूह जिनके पास 1 के अलावा कोई अन्य सामान्य गुणांक नहीं होता, सह-प्राइम कहलाते हैं।

दो सह-प्राइम संख्याओं का LCM उनके गुणनफल के बराबर होता है।

प्रश्न 13: दो सह-प्राइम का HCF है

(a) छोटी संख्या
(b) बड़ी संख्या
(c) संख्याओं का गुणनफल

दो सह-प्राइम संख्याओं का HCF 1 होता है।

इसलिए, सही उत्तर विकल्प (d) है।

प्रश्न 14: सबसे छोटी संख्या जो न तो प्राइम है और न ही कॉम्पोजिट है, है

(d) 3

उत्तर: सबसे छोटी संख्या जो न तो प्राइम है और न ही कॉम्पोजिट है, 1 है।

इसलिए, सही उत्तर विकल्प (b) है।

प्रश्न 15: किसी भी प्राकृतिक संख्या और सबसे छोटे अभाज्य संख्या का गुणनफल है

उत्तर: सबसे छोटी अभाज्य संख्या 2 है।

इसलिए, जब हम किसी भी प्राकृतिक संख्या को गुणा करते हैं, तो हम हमेशा एक सम संख्या प्राप्त करते हैं।

इसलिए, सही उत्तर विकल्प (a) है।

प्रश्न 16: हर गणना संख्या के पास अनंत संख्या होती है

(a) गुणक

(b) गुणा

उत्तर: गुणक वह हैं जो हमें संख्या को किसी भी संख्या से गुणा करने पर प्राप्त होते हैं।

इसलिए, हर गणना संख्या के पास अनंत संख्या के गुणक होते हैं।

प्रश्न 17: दो संख्याओं का गुणनफल 1530 है और उनका HCF 15 है। इन संख्याओं का LCM है

(a) 102

(b) 120

(d) 112

उत्तर:

दो संख्याओं का गुणनफल = दो संख्याओं का HCF × दो संख्याओं का LCM

⇒ 1530 = 15 × दो संख्याओं का LCM

⇒ दो संख्याओं का LCM = 102

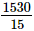
प्रश्न 18: वह सबसे छोटी संख्या जो 15, 20, 24 और 32 में से प्रत्येक से विभाज्य है, है

(a) 960

(b) 480

(d) 640

उत्तर: 15, 20, 24 और 32 का LCM इस प्रकार दिया गया है

15 = 3 × 5 = 3¹ × 5¹

20 = 2 × 2 × 5 = 2² × 5¹

24 = 2 × 2 × 2 × 3 = 2³ × 3¹

32 = 2 × 2 × 2 × 2 × 2 = 2⁵

LCM = 2⁵ × 3¹ × 5¹ = 480

प्रश्न 19: सबसे बड़ा संख्या जो 134 और 167 को 2 बाकी छोड़ते हुए विभाजित करता है, है

(a) 14

(b) 19

(d) 17

उत्तर: पहले हम 134 और 167 से आवश्यक बाकी को घटाते हैं।

इसलिए, हमें 132 और 165 प्राप्त होगा।

132 = 2 × 2 × 3 × 11 = 2² × 3 × 11

165 = 3 × 5 × 11 = 31 × 5 × 11

HCF = 3 × 11 = 33

अत: सबसे बड़ा संख्या जो 134 और 167 को 2 शेषफल छोड़ते हुए विभाजित करता है, वह 33 है।

प्रश्न 20. निम्नलिखित में से कौन सा संख्या एक प्राइम नंबर है?

(a) 91
(b) 81
(c) 87

उत्तर: चूंकि, के गुणांक

91 = 1 × 7 × 13

81 = 1 × 3 × 3 × 3 × 3

87 = 1 × 3 × 29

97 = 1 × 97

इसलिए, 81, 87 और 91 सभी प्राइम नंबर नहीं हैं।

प्रश्न 21. यदि दो संख्याएँ समान हैं, तो

(a) उनका LCM उनके HCF के बराबर है
(b) उनका LCM उनके HCF से कम है
(c) उनका LCM उनके HCF के दो गुना के बराबर है

उत्तर: यदि दो संख्याएँ समान हैं, तो उनका LCM उनके HCF के बराबर है।

प्रश्न 22. a और b दो को-प्राइम हैं। निम्नलिखित में से कौन सा/से सही है?

(a) LCM (a, b) = a × b
(b) HCF (a, b) = 1
(c) दोनों (a) और (b)
(d) न तो (a) और न (b)

उत्तर: ऐसे संख्याओं का समूह जिनके पास 1 के अलावा कोई अन्य सामान्य गुणांक नहीं है, उन्हें को-प्राइम कहा जाता है।

The document आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) have been prepared according to the Class 6 exam syllabus. Information about आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) covers topics like and आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1).

Introduction of आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1)

In this doc you can find the meaning of आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) defined & explained in the simplest way possible. Besides explaining types of आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) theory, EduRev gives you an ample number of questions to practice आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Top Courses for Class 6

View all courses for Class 6

Summary

Sample Paper

Exam

pdf

Important questions

video lectures

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

mock tests for examination

practice quizzes

Objective type Questions

Previous Year Questions with Solutions

past year papers

MCQs

ppt

Semester Notes

Free

Viva Questions

study material

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Extra Questions

shortcuts and tricks

;

Additional Information about आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) for Class 6 Preparation

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Free PDF Download

The आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) now and kickstart your journey towards success in the Class 6 exam.

Importance of आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1)

The importance of आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Notes

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Notes on EduRev are your ultimate resource for success.

आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Class 6 Questions

The "आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) on the App

Students of Class 6 can study आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of आरडी शर्मा समाधान: पूर्ण संख्याएँ (व्यायाम 3.1) is prepared as per the latest Class 6 syllabus.

Education Revolution