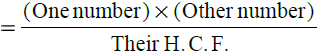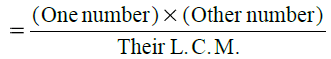आर एस अग्रवाल समाधान: गुणनखंड और गुणन (व्यायाम 2C) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download
प्राइम फैक्टराइजेशन खोजें निम्नलिखित संख्याओं के लिए।
- प्र. 1. 12
- प्र. 2. 18
- प्र. 3. 48
- प्र. 4. 56
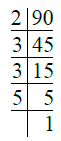
- प्र. 5. 90
- प्र. 6. 136
- प्र. 7. 252
- प्र. 8. 420
- प्र. 9. 637
- प्र. 10. 945
- प्र. 11. 1224
- प्र. 12. 1323
- प्र. 13. 8712
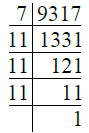
- प्र. 14. 9317
- प्र. 15. 1035
- प्र. 16. 1197
- प्र. 17. 4641
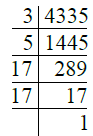
- प्र. 18. 4335
- प्र. 19. 2907
- प्र. 20. 13915
उत्तर: ∴ 12 = 2 × 2 × 3 = 22 × 3
उत्तर: ∴ 18 = 2 × 3 × 3 = 2 × 32
उत्तर: ∴ 48 = 2 × 2 × 2 × 2 × 3 = 24 × 3
उत्तर: ∴ 56 = 2 × 2 × 2 × 7 = 23 × 7
उत्तर: ∴ 90 = 2 × 3 × 3 × 5 = 2 × 32 × 5
उत्तर: ∴ 136 = 2 × 2 × 2 × 17 = 23 × 17
उत्तर: ∴ 252 = 2 × 2 × 3 × 3 × 7 = 22 × 32 × 7
उत्तर: ∴ 420 = 2 × 2 × 3 × 5 × 7 = 22 × 3 × 5 × 7
उत्तर: ∴ 637 = 7 × 7 × 13 = 72 × 13
उत्तर: ∴ 945 = 3 × 3 × 3 × 5 × 7 = 33 × 5 × 7
उत्तर: ∴ 1224 = 2 × 2 × 2 × 3 × 3 × 17 = 23 × 32 × 17
उत्तर: ∴ 1323 = 3 × 3 × 3 × 7 × 7 = 33 × 72
उत्तर: ∴ 8712 = 2 × 2 × 2 × 3 × 3 × 11 × 11 = 23 × 32 × 112
उत्तर: ∴ 9317 = 7 × 11 × 11 × 11 = 7 × 113
उत्तर: ∴ 1035 = 3 × 3 × 5 × 23 = 32 × 5 × 23
उत्तर: ∴ 1197 = 3 × 3 × 7 × 19 = 32 × 7 × 19
उत्तर: ∴ 4641 = 3 × 7 × 13 × 17
उत्तर: ∴ 4335 = 3 × 5 × 17 × 17 = 3 × 5 × 172
उत्तर: ∴ 2907 = 3 × 3 × 17 × 19 = 32 × 17 × 19
उत्तर: ∴ 13915 = 5 × 11 × 11 × 23 = 5 × 112 × 23
सर्वाधिक सामान्य गुणांक (H.C.F.) और न्यूनतम गुणांक (L.C.M.)
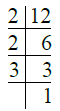
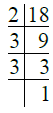
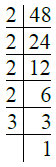
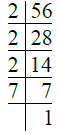
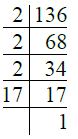
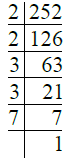
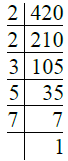
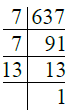
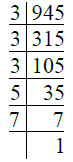
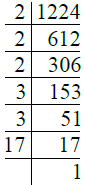
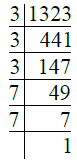
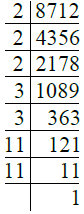
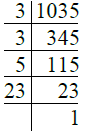
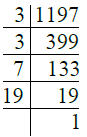
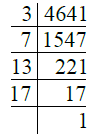
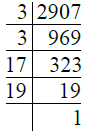

दो या अधिक दिए गए संख्याओं का सबसे बड़ा संख्या जो एक सामान्य गुणांक है, उसे उच्चतम सामान्य गुणांक (H.C.F.) या महत्तम सामान्य भाजक (G.C.D.) या महत्तम सामान्य माप (G.C.M.) कहा जाता है। H.C.F. ज्ञात करने के लिए (प्राइम फैक्टराइजेशन विधि द्वारा)। सबसे पहले, हम दिए गए संख्याओं का प्राइम फैक्टराइजेशन निकालते हैं। फिर, सभी सामान्य प्राइम फैक्टर का गुणनफल, प्रत्येक सामान्य प्राइम फैक्टर की न्यूनतम शक्ति का उपयोग करते हुए, दिए गए संख्याओं का H.C.F. होता है। H.C.F. ज्ञात करने के लिए (डिवीजन विधि द्वारा)। दो दिए गए संख्याओं का H.C.F. निकालने के लिए, हम सबसे बड़ी संख्या को छोटी संख्या से विभाजित करते हैं। उसके बाद, हम भाजक को शेषफल से विभाजित करते हैं। इस प्रक्रिया को तब तक दोहराते रहें जब तक शेषफल शून्य न हो जाए। तब, अंतिम भाजक दिए गए संख्याओं का आवश्यक H.C.F. होता है। दो से अधिक संख्याओं का H.C.F. निकालने के लिए, सबसे पहले हम दो संख्याओं का H.C.F. निकालते हैं। इस H.C.F. और तीसरी संख्या का H.C.F. इन तीन संख्याओं का H.C.F. देता है, और इसी तरह आगे बढ़ते हैं।
न्यूनतम सामान्य गुणांक (L.C.M.)
दो या अधिक संख्याओं का न्यूनतम सामान्य गुणांक सबसे छोटा संख्या है जो प्रत्येक संख्या का गुणांक है।
L.C.M. ज्ञात करने के लिए (प्राइम फैक्टराइजेशन विधि द्वारा)। दो या अधिक संख्याओं का L.C.M. निकालने के लिए, हम दिए गए संख्याओं का प्राइम फैक्टराइजेशन लिखते हैं। फिर, सभी विभिन्न प्राइम फैक्टर का गुणनफल, प्रत्येक सामान्य प्राइम फैक्टर की सबसे बड़ी शक्ति का उपयोग करते हुए, इन संख्याओं का आवश्यक L.C.M. होता है।
L.C.M. ज्ञात करने के लिए (डिवीजन विधि द्वारा)।
इस विधि में, हम दिए गए संख्याओं को किसी भी क्रम में एक पंक्ति में व्यवस्थित करते हैं। हम एक ऐसे संख्या से भाग करते हैं जो दिए गए संख्याओं में से कम से कम दो को सही-सही विभाजित करता है और उन संख्याओं को आगे बढ़ाते हैं जो विभाजित नहीं होती हैं। यह प्रक्रिया तब तक दोहराई जाती है जब तक दिए गए संख्याओं में से कोई दो एक ही संख्या से विभाजित नहीं होते। विभाजकों और अविभाजित संख्याओं का गुणनफल दिए गए संख्याओं का आवश्यक L.C.M. है।
दिए गए संख्याओं के H.C.F. और L.C.M. के गुण:
- 1. दिए गए संख्याओं का H.C.F. किसी भी दिए गए संख्या से अधिक नहीं होता।
- 2. दो सह-प्राइम संख्याओं का H.C.F. 1 होता है।
- 3. दिए गए संख्याओं का L.C.M. किसी भी दिए गए संख्या से कम नहीं होता।
- 4. दो सह-प्राइम संख्याओं का L.C.M. उनके गुणनफल के बराबर होता है।
- 5. दिए गए संख्याओं का H.C.F. हमेशा उनके L.C.M. का एक गुणांक होता है।
- 6. यदि a और b दो दिए गए संख्याएँ हैं और a, b का एक गुणांक है, तो उनका H.C.F. = a और उनका L.C.M. = b होता है।
- 7. यदि दो संख्याएँ दी गई हैं, तो उन दो संख्याओं का गुणनफल = उनके H.C.F. और L.C.M. का गुणनफल।
टिप: किसी भी दो दिए गए संख्याओं के लिए, हमारे पास है:
- (i) L.C.M.
- (ii) H.C.F.