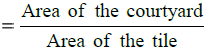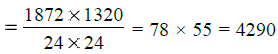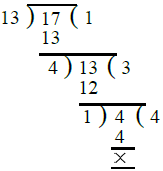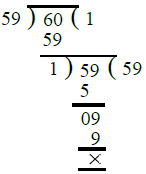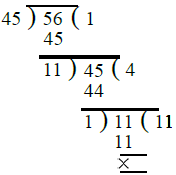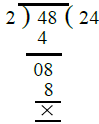Open App

Class 6 Exam > Class 6 Notes > गणित (गणित प्रकाश ) कक्षा 6 > आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी)

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 PDF Download

सबसे पहले, हम 161 और 207 का H.C.F. खोजते हैं। निम्नलिखित संख्याओं का H.C.F. खोजें, प्राइम फैक्टराइजेशन विधि का उपयोग करते हुए:

Q.1. 84, 98। उत्तर: हमारे पास है

84 = 2 × 2 × 3 × 7 = 2² × 3 × 7
98 = 2 × 7 × 7 = 2 × 7²

∴ H.C.F. = 2 × 7 = 14।

Q.2. 170, 238। उत्तर: हमारे पास है

170 = 2 × 5 × 17
238 = 2 × 7 × 17

∴ H.C.F. of 170 and 238 = 2 × 17 = 34।

Q.3. 504, 980। उत्तर: हमारे पास है

504 = 2 × 2 × 2 × 3 × 3 × 7 = 2³ × 3² × 7
980 = 2 × 2 × 5 × 7 × 7 = 2² × 5 × 7²

∴ H.C.F. of 504 and 980 = 2 × 7 = 4 × 7 = 28।

Q.4. 72, 108, 180। उत्तर: हमारे पास है

72 = 2 × 2 × 2 × 3 × 3 = 2³ × 3²
108 = 2 × 2 × 3 × 3 × 3 = 2² × 3³
180 = 2 × 2 × 3 × 3 × 5 = 2² × 3² × 5

∴ H.C.F. of 72, 108, 180 = 2² × 3² = 4 × 9 = 36।

Q.5. 84, 120, 138। उत्तर: हमारे पास है

84 = 2 × 2 × 3 × 7 = 2² × 3 × 7
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3 × 5
138 = 2 × 3 × 23

∴ H.C.F. of 84, 120 and 138 = 2 × 3 = 6।

Q.6. 106, 159, 371। उत्तर: हमारे पास है

106 = 2 × 53
159 = 3 × 53
371 = 7 × 53

∴ H.C.F. of 106, 159, 371 = 53।

Q.7. 272, 425। उत्तर: हमारे पास है

272 = 2 × 2 × 2 × 2 × 17 = 2⁴ × 17
425 = 5 × 5 × 17 = 5² × 17

∴ H.C.F. of 272 and 425 = 17।

Q.8. 144, 252, 630। उत्तर: हमारे पास है

144 = 2 × 2 × 2 × 2 × 3 × 3 = 2⁴ × 3²
252 = 2 × 2 × 3 × 3 × 7 = 2² × 3² × 7
630 = 2 × 3 × 3 × 5 × 7 = 2 × 3² × 5 × 7

∴ H.C.F. of 144, 252 and 630 = 2 × 3² = 2 × 9 = 18।

Q.9. 1197, 5320, 4389। उत्तर: हमारे पास है

1197 = 3 × 3 × 7 × 19 = 3² × 7 × 19
5320 = 2 × 2 × 2 × 5 × 7 × 19 = 2³ × 5 × 7 × 19
4389 = 7 × 3 × 11 × 19

∴ H.C.F. of 1197, 5320, 4389 = 7 × 19 = 133।

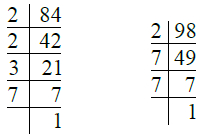
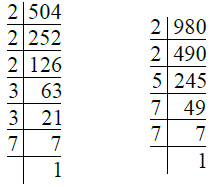
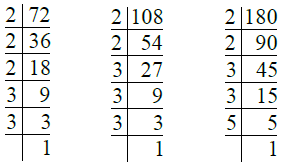
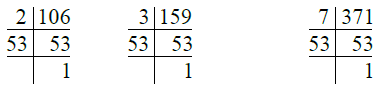
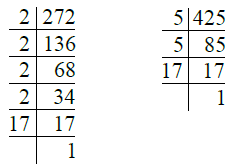
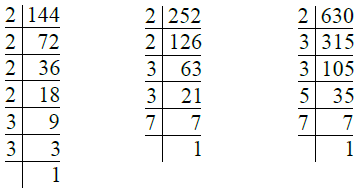
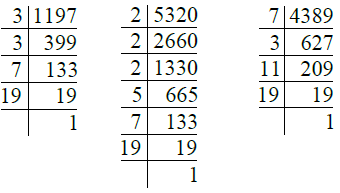
आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

संख्याओं का H.C.F. निकालने के लिए विभाजन विधि का उपयोग करें:

प्र.10. 58, 70।

उत्तर: विभाजन विधि द्वारा, हमें मिलता है: ∴ 58 और 70 का H.C.F. = 2।

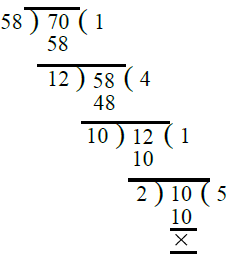
प्र.11. 399, 437।

उत्तर: विभाजन विधि द्वारा, हमें मिलता है: ∴ 399 और 437 का H.C.F. = 19।

प्र.12. 1045, 1520।

हल: विभाजन विधि द्वारा, हमें मिलता है: ∴ 1045 और 1520 का H.C.F. = 95।

प्र.13. 1965, 2096।

उत्तर: विभाजन विधि द्वारा, हमें मिलता है: ∴ 1965 और 2096 का H.C.F. = 131।

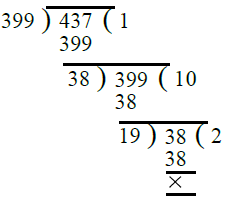
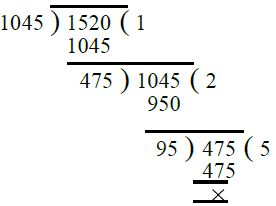
प्र.14. 2241, 2324।

उत्तर: विभाजन विधि द्वारा, हमें मिलता है: ∴ 2241 और 2324 का H.C.F. = 83।

प्र.15. 658, 940, 1128।

पहले, हम 658 और 940 का H.C.F. निकालते हैं। ∴ 658 और 940 का H.C.F. = 94।
अब, हम 94 और 1128 का H.C.F. निकालते हैं। ∴ 94 और 1128 का H.C.F. = 94।

इसलिए, 658, 940 और 1128 का H.C.F. = 94।

प्र.16. 754, 1508, 1972।

पहले, हम 754 और 1508 का H.C.F. निकालते हैं। ∴ 754 और 1508 का H.C.F. = 754।
अब, हम 754 और 1972 का H.C.F. निकालते हैं। ∴ 754 और 1972 का H.C.F. = 58।

इसलिए, 754, 1508 और 1972 का H.C.F. = 58।

प्र.17. 391, 425, 527।

पहले, हम 391 और 425 का H.C.F. निकालते हैं। ∴ 391 और 425 का H.C.F. = 17।
अब, हम 17 और 527 का H.C.F. निकालते हैं। ∴ 17 और 527 का H.C.F. = 17।

इसलिए, 391, 425 और 527 का H.C.F. = 17।

प्र.18. 1794, 2346, 4761।

पहले, हम 1794 और 2346 का H.C.F. निकालते हैं। ∴ 1794 और 2346 का H.C.F. = 138।
अब, हम 138 और 4761 का H.C.F. निकालते हैं। ∴ 138 और 4761 का H.C.F. = 69।

इसलिए, 1794, 2346 और 4761 का H.C.F. = 69।

प्र.19. 59, 97।

उत्तर: पहले, हम 59 और 97 का H.C.F. निकालते हैं। ∴ 59 और 97 का H.C.F. = 1। इस प्रकार, 59 और 97 को-प्राइम हैं।

प्र.20. 161, 192।

उत्तर: पहले, हम 161 और 192 का H.C.F. निकालते हैं। ∴ 161 और 192 का H.C.F. = 1। इस प्रकार, 161 और 192 को-प्राइम हैं।

प्र.21. 343, 432।

उत्तर: पहले, हम 343 और 432 का H.C.F. निकालते हैं। ∴ 343 और 432 का H.C.F. = 1। इस प्रकार, 343 और 432 को-प्राइम हैं।

प्र.22. 512, 945।

उत्तर: पहले, हम 512 और 945 का H.C.F. निकालते हैं।

∴ 512 और 945 का H.C.F. 1 है। इसलिए 512 और 945 को-प्राइम हैं।

Q.23. 385, 621।
उत्तर: सबसे पहले, हम 385 और 621 का H.C.F. निकालते हैं। ∴ 385 और 621 का H.C.F. 1 है। इसलिए 385 और 621 को-प्राइम हैं।

Q.24. 847, 1014।
उत्तर: सबसे पहले, हम 847 और 1014 का H.C.F. निकालते हैं। ∴ 847 और 1014 का H.C.F. 1 है। इसलिए 847 और 1014 को-प्राइम हैं।

Q.25. सबसे बड़ा संख्या ज्ञात करें जो 615 और 963 को 6 का शेष छोड़कर विभाजित करती है।
उत्तर: स्पष्ट है कि हमें सबसे बड़ा संख्या ज्ञात करना है जो (615 – 6) और (963 – 6) को ठीक से विभाजित करता है।
तो, आवश्यक संख्या = 615 – 6 = 609 और 963 – 6 = 957 का H.C.F. ∴ आवश्यक सबसे बड़ा संख्या = 87।

Q.26. सबसे बड़ा संख्या ज्ञात करें जो 2011 और 2623 को क्रमशः 9 और 5 का शेष छोड़कर विभाजित करती है।
उत्तर: स्पष्ट है कि हमें सबसे बड़ा संख्या ज्ञात करना है जो 2011 – 9 = 2002 और 2623 – 5 = 2618 को ठीक से विभाजित करता है।
तो, आवश्यक सबसे बड़ा संख्या = 2002 और 2618 का H.C.F. ∴ आवश्यक सबसे बड़ा संख्या = 154।

Q.27. सबसे बड़ा संख्या ज्ञात करें जो 445, 572 और 699 को क्रमशः 4, 5, और 6 का शेष छोड़कर विभाजित करती है।
उत्तर: स्पष्ट है कि हमें सबसे बड़ा संख्या ज्ञात करना है जो (445 – 4), (572 – 5) और (699 – 6) को ठीक से विभाजित करता है।
तो, आवश्यक संख्या = 441, 567 और 693 का H.C.F.। सबसे पहले, हम 441 और 567 का H.C.F. निकालते हैं। ∴ 441 और 567 का H.C.F. 63 है।
इसके बाद, 63 और 693 का H.C.F. 63 है। इसलिए आवश्यक संख्या = 63।

Q.28. निम्नलिखित भिन्नों को निम्नतम रूप में घटित करें:
(i) (ii) (iii)
उत्तर: (i) दी गई भिन्न = सबसे पहले, हम 161 और 207 का H.C.F. निकालते हैं। ∴ 161 और 207 का H.C.F. = 23 है। दी गई भिन्न के अंश और हर को 23 से विभाजित करने पर हमें मिलता है:
(ii) दी गई भिन्न: सबसे पहले, हम 517 और 799 का H.C.F. निकालते हैं। ∴ 517 और 799 का H.C.F. 47 है। दी गई भिन्न के अंश और हर को 47 से विभाजित करने पर हमें मिलता है:
(iii) दी गई भिन्न: सबसे पहले, हम 296 और 481 का H.C.F. निकालते हैं। ∴ 296 और 481 का H.C.F. 37 है।

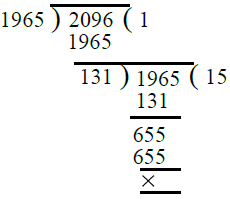
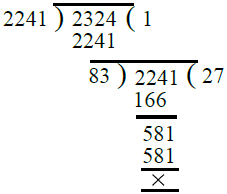
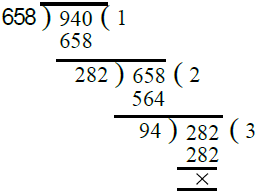
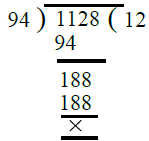
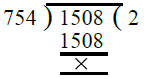
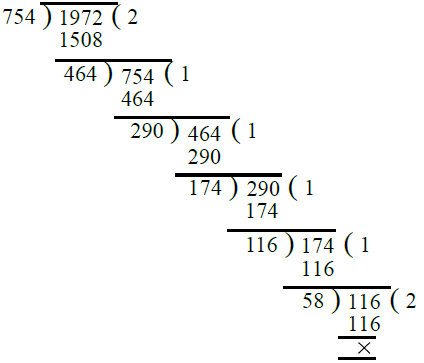
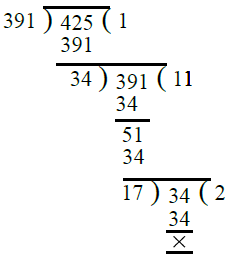
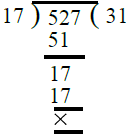
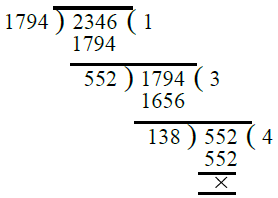
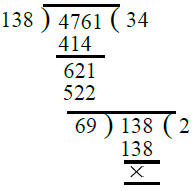
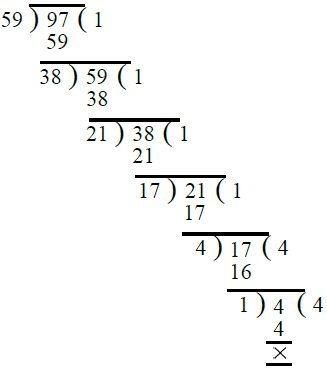
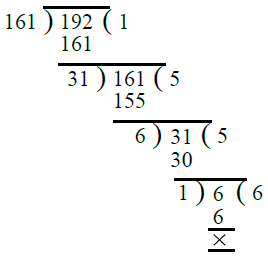
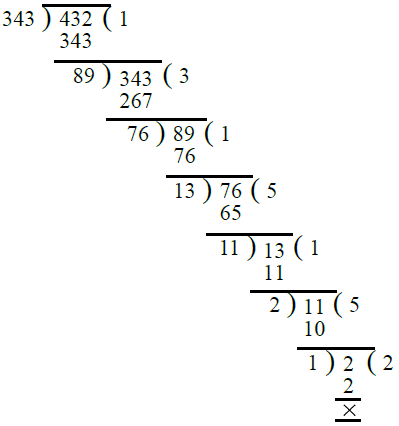
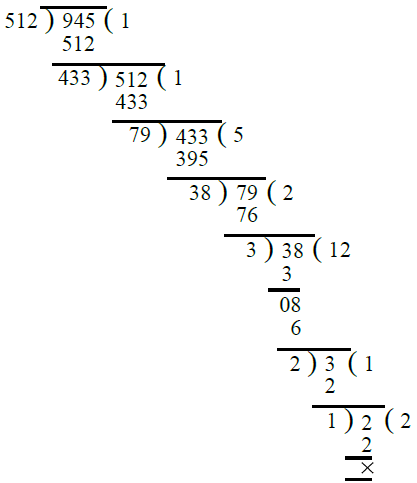
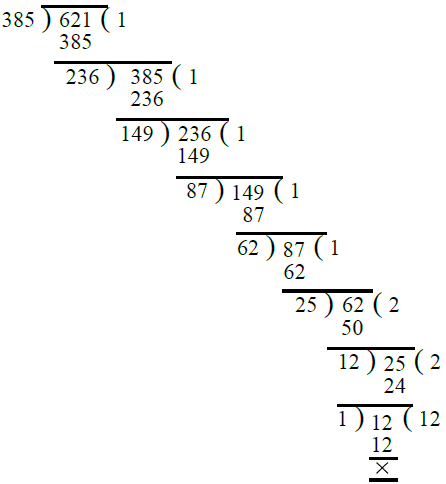
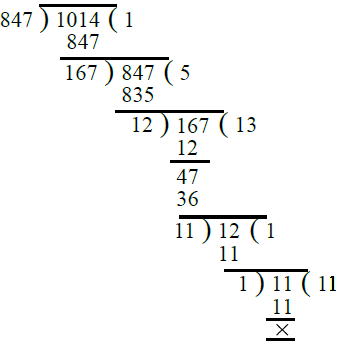
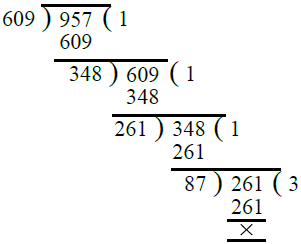
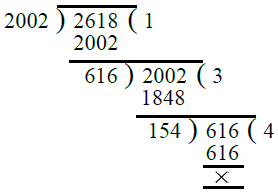
दी गई भिन्न के अंश और हर को 37 से विभाजित करने पर हमें प्राप्त होता है।

प्रश्न 29: तीन लकड़ी के टुकड़े जिनकी लंबाई क्रमशः 42 मीटर, 49 मीटर और 63 मीटर है, को समान लंबाई की तख्तियों में विभाजित करना है। प्रत्येक तख्ती की अधिकतम संभव लंबाई क्या है? उत्तर:

तीन लकड़ी के टुकड़ों की लंबाई = 42 मीटर, 49 मीटर, 63 मीटर
प्रत्येक तख्ती की अधिकतम संभव लंबाई = H.C.F. (42 मीटर, 49 मीटर और 63 मीटर)

पहले हम 42 और 49 का H.C.F. निकालते हैं।

∴ 42 और 49 का H.C.F. = 7

अब हम 7 और 63 का H.C.F. निकालते हैं।

∴ 7 और 63 का H.C.F. = 7

∴ 42 मीटर, 49 मीटर और 63 मीटर का H.C.F. = 7 मीटर

इसलिए आवश्यक तख्ती की लंबाई = 7 मीटर।

प्रश्न 30: तीन अलग-अलग कंटेनर में क्रमशः 403 लिटर, 434 लिटर और 465 लिटर दूध है। एक ऐसा कंटेनर ढूंढें जो सभी कंटेनरों के दूध को एक सटीक संख्या में माप सके। उत्तर:

तीन अलग-अलग कंटेनरों में दूध की मात्रा = 403 लिटर, 434 लिटर और 465 लिटर
स्पष्ट है कि आवश्यक कंटेनर की अधिकतम क्षमता = H.C.F. (403 लिटर, 434 लिटर, 465 लिटर)

हमारे पास:

403 = 13 × 31
434 = 2 × 7 × 31
465 = 5 × 3 × 31

इसलिए 403 लिटर, 434 लिटर और 465 लिटर का H.C.F. = 31 लिटर

आवश्यक कंटेनर की अधिकतम क्षमता = 31 लिटर।

प्रश्न 31: 527 सेब, 646 नाशपाती और 748 संतरे हैं। इन्हें समान संख्या में फलों वाले ढेरों में व्यवस्थित करना है। प्रत्येक ढेर में फलों की अधिकतम संख्या क्या है? कितने ढेर बनते हैं? उत्तर:

दी गई फल = 527 सेब, 646 नाशपाती और 748 संतरे
स्पष्ट है कि प्रत्येक ढेर में फलों की अधिकतम संख्या = H.C.F. (527, 646 और 748)

हमारे पास:

527 = 17 × 31
646 = 2 × 17 × 19
748 = 2 × 2 × 11 × 17

इसलिए 527, 646 और 748 का H.C.F. = 17

∴ प्रत्येक ढेर में आवश्यक फलों की संख्या = 17

कुल फलों की संख्या = 527 + 646 + 748 = 1921

ढेरों की संख्या =

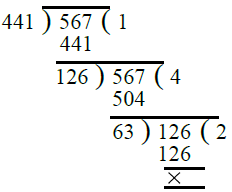
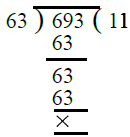
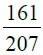
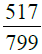
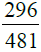
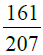
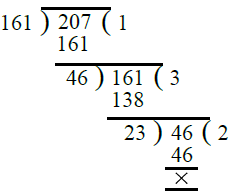
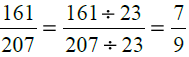
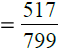
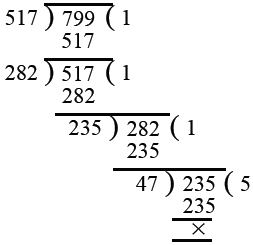
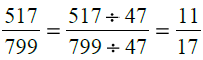
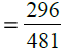
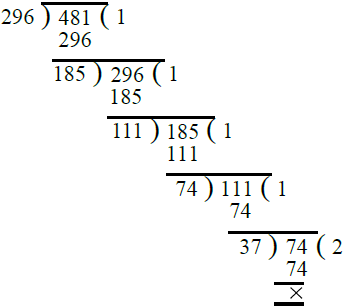
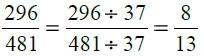
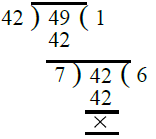
प्रश्न 32: लंबी टेप निर्धारित करें जिसका उपयोग लंबाई 7 मीटर, 3 मीटर 85 सेंटीमीटर और 12 मीटर 95 सेंटीमीटर को सटीक रूप से मापने के लिए किया जा सके।

उत्तर: दी गई लंबाइयाँ हैं:

7 मीटर = 7 × 100 सेंटीमीटर = 700 सेंटीमीटर
3 मीटर 85 सेंटीमीटर = (3 × 100 + 85) सेंटीमीटर = 385 सेंटीमीटर
12 मीटर 95 सेंटीमीटर = (12 × 100 + 95) सेंटीमीटर = 1295 सेंटीमीटर

स्पष्ट है कि आवश्यक सबसे लंबी टेप की लंबाई है:

H.C.F. (700 सेंटीमीटर, 385 सेंटीमीटर और 1295 सेंटीमीटर)

हमारे पास:

700 = 2 × 2 × 5 × 5 × 7 = 2² × 5² × 7
385 = 5 × 7 × 11
1295 = 5 × 7 × 37

अतः H.C.F. (700, 385 और 1295) = 5 × 7 = 35

आवश्यक सबसे लंबी टेप की लंबाई = 35 सेंटीमीटर.

प्रश्न 33: एक आयताकार आँगन की लंबाई 18 मीटर 72 सेंटीमीटर और चौड़ाई 13 मीटर 20 सेंटीमीटर है। इसे समान आकार की वर्ग टाइलों से पक्का करना है। ऐसी टाइलों की न्यूनतम संख्या ज्ञात करें।

उत्तर: आँगन की लंबाई = 18 मीटर 72 सेंटीमीटर = (18 × 100 + 72) सेंटीमीटर = 1872 सेंटीमीटर

आँगन की चौड़ाई = 13 मीटर 20 सेंटीमीटर = (13 × 100 + 20) सेंटीमीटर = 1320 सेंटीमीटर

प्रत्येक वर्ग टाइल की सबसे बड़ी ओर = H.C.F. (1872 सेंटीमीटर और 1320 सेंटीमीटर)

अब:

1872 = 2 × 2 × 2 × 2 × 9 × 13 = 2⁴ × 3² × 13
1320 = 2 × 2 × 2 × 3 × 5 × 11 = 2³ × 3 × 5 × 11

तो, H.C.F. (1872 और 1320) = 2³ × 3 = 8 × 3 = 24

अतः वर्ग टाइल की सबसे बड़ी ओर = 24 सेंटीमीटर

अब आँगन का क्षेत्रफल = लंबाई × चौड़ाई = 1872 × 1320 सेंटीमीटर²

एक वर्ग टाइल का क्षेत्रफल = ओर × ओर = 24 × 24 सेंटीमीटर²

अतः ऐसी टाइलों की न्यूनतम संख्या:

प्रश्न 34: निम्नलिखित का H.C.F. ज्ञात करें:

(i) दो अभाज्य संख्याएँ
(ii) दो अनुक्रमिक संख्याएँ
(iii) दो सह-प्राइम संख्याएँ
(iv) 2 और एक सम संख्या

उत्तर:

(i) मान लें कि दो अभाज्य संख्याएँ 13 और 17 हैं, हम इनका H.C.F. ज्ञात करते हैं: H.C.F. = 1.
(ii) मान लें कि दो अनुक्रमिक संख्याएँ 59 और 60 हैं। इनका H.C.F. ज्ञात करते हैं:

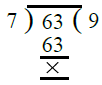
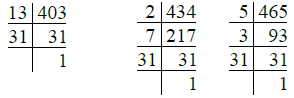
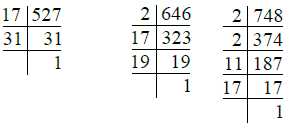
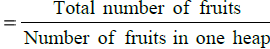
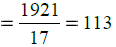
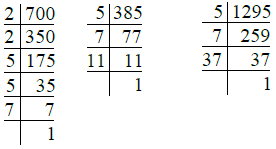
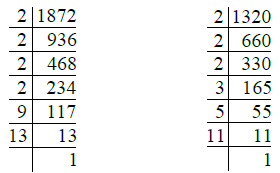
∴ दो लगातार संख्याओं 59 और 60 का H.C.F. = 1। (iii) मान लेते हैं कि दो को-प्राइम संख्याएँ 45 और 56 हैं। हम 45 और 56 का H.C.F. निम्नलिखित प्रकार से निकालते हैं: ∴ 45 और 56 का H.C.F. = 1। (iv) हम 2 और एक अन्य सम संख्या = 48 लेते हैं और 2 और 48 का H.C.F. निम्नलिखित प्रकार से निकालते हैं: ∴ 2 और सम संख्या 48 का H.C.F. = 2।

The document आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 is a part of the Class 6 Course गणित (गणित प्रकाश ) कक्षा 6.

All you need of Class 6 at this link: Class 6

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

About this Document

Oct 02, 2025 Last updated

Related Exams

Class 6

Document Description: आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) for Class 6 2025 is part of गणित (गणित प्रकाश ) कक्षा 6 preparation. The notes and questions for आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) have been prepared according to the Class 6 exam syllabus. Information about आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) covers topics like and आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी).

Introduction of आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) in English is available as part of our गणित (गणित प्रकाश ) कक्षा 6 for Class 6 & आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) in Hindi for गणित (गणित प्रकाश ) कक्षा 6 course. Download more important topics related with notes, lectures and mock test series for Class 6 Exam by signing up for free. Class 6: आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Description

Full syllabus notes, lecture & questions for आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for गणित (गणित प्रकाश ) कक्षा 6 | Best notes, free PDF download

Information about आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी)

In this doc you can find the meaning of आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) defined & explained in the simplest way possible. Besides explaining types of आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) theory, EduRev gives you an ample number of questions to practice आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) tests, examples and also practice Class 6 tests

	गणित (गणित प्रकाश ) कक्षा 6 236 docs

गणित (गणित प्रकाश ) कक्षा 6

236 docs

Join Course for Free

Download as PDF

Explore Courses for Class 6 exam

ppt

Summary

Semester Notes

mock tests for examination

past year papers

Objective type Questions

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Extra Questions

study material

Sample Paper

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Important questions

practice quizzes

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) | गणित (गणित प्रकाश ) कक्षा 6 - Class 6

Free

Previous Year Questions with Solutions

pdf

Exam

shortcuts and tricks

video lectures

MCQs

Viva Questions

;

Additional Information about आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) for Class 6 Preparation

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Free PDF Download

The आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) is an invaluable resource that delves deep into the core of the Class 6 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) now and kickstart your journey towards success in the Class 6 exam.

Importance of आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी)

The importance of आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) cannot be overstated, especially for Class 6 aspirants. This document holds the key to success in the Class 6 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Notes

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Notes on EduRev are your ultimate resource for success.

आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Class 6 Questions

The "आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) on the App

Students of Class 6 can study आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of आरएस अग्रवाल समाधान: गुणक और गुणा (व्यायाम 2डी) is prepared as per the latest Class 6 syllabus.

Education Revolution