Symmetrical Designs NCERT Solutions | Mathematics (Maths Mela) Class 5 - New NCERT PDF Download
| Table of contents |

|
| Page No. 136 |

|
| Page No. 137-138 |

|
| Page No. 139-140 |

|
| Page No. 141 |

|
Page No. 136
Alphabet Cutout
Q1: Which of the following alphabet cutouts can be made by just drawing half (1/2) or quarter (1/4) of the letter? You can do it by drawing lines of symmetry on the letters. Ans:
Ans:
Letters with (1/4) symmetry.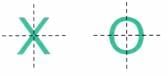 Letters with (1/2) symmetry.
Letters with (1/2) symmetry.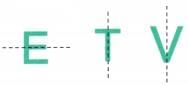
Q2: Which of the letters have a horizontal line of symmetry? _________________
Ans:
Q3: Which of the letters have a vertical line of symmetry? ____________________
Ans: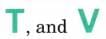
Q4: Which letters have both vertical and horizontal lines of symmetry?________
Ans:
Let Us Do
Q1: Use lines of symmetry to make paper cutouts of diya, boat, and other designs. Look along the border of the page to fine the pictures.
Ans:
Do it yourself.
Page No. 137-138
Let Us Make a Windmill Firki
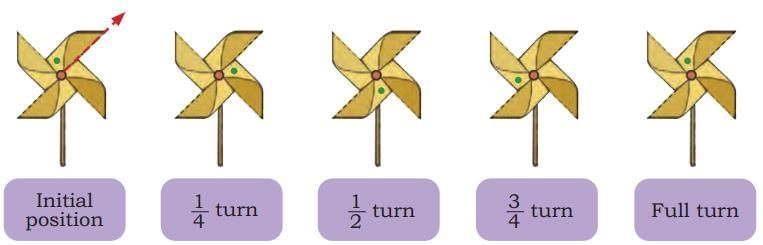 Ans:
Ans:Yes
Q1: Observe the letters below. Do they look the same when turned? Dots have been marked on the letters to keep track of the orientation of letters. You may also cut out the letters and fix the centre point of the letter by a nail or use tracing paper to check if the letter looks the same when turned.
 Ans:
Ans: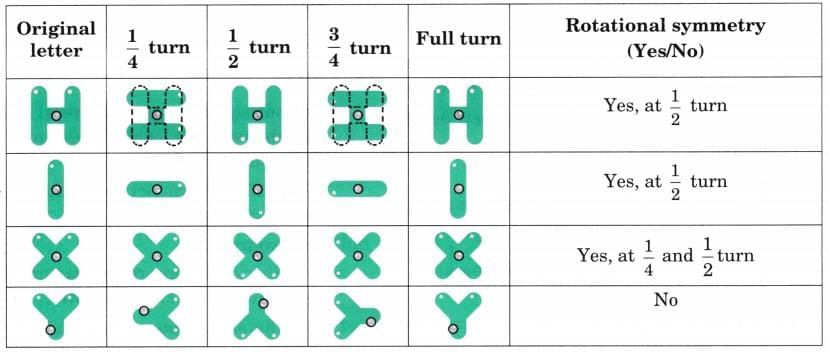
Let Us Do
 Ans:
Ans:Horizontal line of symmetry.
 Both horizontal and vertical line of symmetry
Both horizontal and vertical line of symmetry
Q2: Which digit(s) have reflection symmetry?
Ans: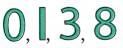
Q3: Which digit(s) have rotational symmetry?
Ans:
Q4: Which digit(s) have both rotational and reflection symmetries?
Ans:
Q5: Now, let us look at the following numbers: ||, |00|
Do these have
(a) rotational symmetry,
(b) reflection symmetry or
(c) both symmetries?
Ans:
||, |00| have both rotational and reflection symmetry.
Q6: Give examples of 2-, 3-, and 4-digit numbers which have rotational symmetry, reflection symmetry, or both.
Ans:
2-digit number which have rotational and reflection symmetry both is ||.
3- digit numbers which have rotational and reflection symmetry both are ||| , |0|.
4- digit numbers which have rotational and reflection symmetry both are |||, |00|
Page No. 139-140
Making Designs
Q1: (a) Does the design have rotational symmetry?
Yes/No. Ans:
Ans:
No, it does not look the same after any rotation
i.e., 1/2 or 1/4 turn.
(b) Try to change the design by adding some shape(s) so that the new design looks the same after a 1/2 turn. Draw the new design 2 in your notebook.
Ans:
Do it yourself.
(c) Now try to modify or add more shapes so that the new design looks the same after ~ turn.
Draw the new design in your notebook.
Ans:
Do it yourself.
(d) Do the new designs have reflection symmetry? If yes, draw the lines of symmetry.
Ans:
Do it yourself.
Let Us Think
Q1: Does this design look the same after 1/2 turn? Ans:
Ans:
Yes, the design looks the same after 1/2 turn.
Q2: Does this design looks the same after 1/4 turn? Ans:
Ans:
No, the design does not look the same after 1/4 turn.
Colour the square given in the adjoining figure using two colours so that the design looks the same after every 1/4 turn.
How many times does this shape look the. same during a full turn?
Q3: Do these designs have reflection symmetry also? Draw the line(s) of symmetry.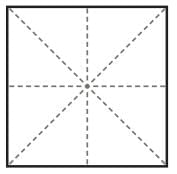 Ans:
Ans:
The image looks the same after every 1/4 turn.
During a full turn it looks same four times. The shaded design does not have reflection symmetry.
Let Us Do
Q1: Cut out squares and equilateral triangles with the same side length. These are provided at the end of the book.
Make different symmetrical designs by using these two shapes. Ans:
Ans:
Do it yourself.
Q2: Does this shape have reflection symmetry? If yes, draw its line(s) of symmetry.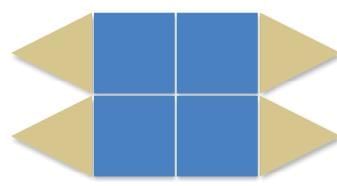 Ans:
Ans:
Yes the shape has reflection symmetry. Its lines of symmetry are drawn as shown in the picture below.
Q3: Does it have rotational symmetry? If yes, at which turn?
Ans:
The shape has rotational symmetry of 1/2 turn also.
Q4: Does it have both symmetries?
Ans:
Yes, the shape have both symmetries.
Let Us Explore
Q1: Below are images of wooden blocks and a part of their prints. Match each block to its correct print by drawing a line. One is done for you. Ans:
Ans: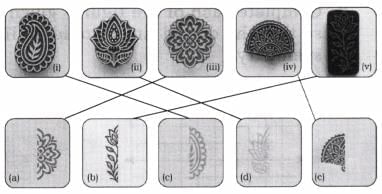
Page No. 141
Let Us Do
Q1: Observe the shapes given on the border. Which of the shapes have reflection symmetry? Put a mark on them. Put a on the shapes that have rotational symmetry. The design A looks the same after every 1/4 turn.
The design A looks the same after every 1/4 turn.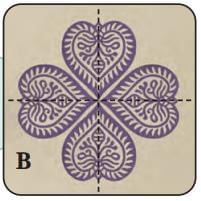 The design B looks the same after every ____________ turn. This design has _________________symmetry.
The design B looks the same after every ____________ turn. This design has _________________symmetry.
Ans:
Do it yourself.

Project Work
Q1: Create symmetrical patterns and designs using vegetable blocks. Some are shown below.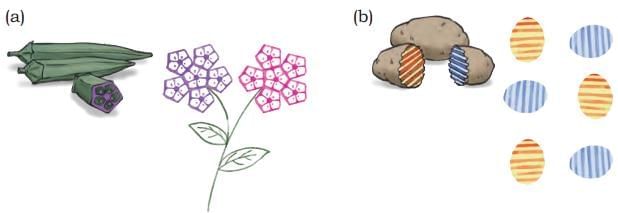 Ans:
Ans:
Do it yourself.
|
35 videos|322 docs|7 tests
|
FAQs on Symmetrical Designs NCERT Solutions - Mathematics (Maths Mela) Class 5 - New NCERT
| 1. What are symmetrical designs and why are they important in art and mathematics? |  |
| 2. How can symmetrical designs be created using simple shapes? |  |
| 3. What are some real-life examples of symmetrical designs? |  |
| 4. In what ways can symmetrical designs be applied in educational settings for younger students? |  |
| 5. How does the concept of symmetry relate to the study of shapes and patterns in mathematics? |  |















