Numerical Questions : WORK & ENERGY - Class 9 PDF Download

Some Numerical Questions: WORK & ENERGY

 Q. 1 A force of 10N causes a displacement of 2m in a body in its direction. Calculate the work done by force.
Ans: Work done (W) = Force (F) × Displacement (d)
$W=10\hspace{0.17em}N\times 2\hspace{0.17em}m=20\hspace{0.17em}JW\; =\; 10\; \backslash ,\; \backslash text\{N\}\; \backslash times\; 2\; \backslash ,\; \backslash text\{m\}\; =\; 20\; \backslash ,\; \backslash text\{J\}$J
Ans: 20 J

Q. 2 How much force is applied on the body when 150 J of work is done in displacing the body through a distance of 10m in the direction of force?
Ans: Using the formula $W=F\times dW\; =\; F\; \backslash times\; d$, we rearrange to find $F=\frac{W}{d}F\; =\; \backslash frac\{W\}\{d\}$.
$F=\frac{150}{10}=15\hspace{0.17em}NF\; =\; \backslash frac\{150\; \backslash ,\; \backslash text\{J\}\}\{10\; \backslash ,\; \backslash text\{m\}\}\; =\; 15\; \backslash ,\; \backslash text\{N\}$
Ans: 15 N

Q. 3 A body of 5kg is raised to 2m. Find the work done.
Ans: Work done $W=m\times g\times hW\; =\; m\; \backslash times\; g\; \backslash times\; h$, where $g=9.8\hspace{0.17em}m/s2g\; =\; 9.8\; \backslash ,\; \backslash text\{m/s\}^2$g.
$W=5\times 9.8\times 2=98\hspace{0.17em}JW\; =\; 5\; \backslash times\; 9.8\; \backslash times\; 2\; =\; 98\; \backslash ,\; \backslash text\{J\}$J
Ans: 98 J

Q. 4 A work of 4900 J is done on a load of mass 50 kg to lift it to a certain height. Calculate the height through which the load is lifted.
Ans: Using $W=m\times g\times hW\; =\; m\; \backslash times\; g\; \backslash times\; h$, rearrange to $h=\frac{\mathrm{W/}}{m}$.
$h=\frac{4900}{\mathrm{/50}}=10\hspace{0.17em}mh\; =\; \backslash frac\{4900\}\{50\; \backslash times\; 9.8\}\; =\; 10\; \backslash ,\; \backslash text\{m\}$m
Ans: 10 m

Q. 5 An engine does 54,000 J of work by exerting a force of 6000 N. What is the displacement?
Ans: Displacement $d=\frac{W}{F}d\; =\; \backslash frac\{W\}\{F\}$d=FW.
$d=\frac{54000}{6000}=9\hspace{0.17em}md\; =\; \backslash frac\{54000\}\{6000\}\; =\; 9\; \backslash ,\; \backslash text\{m\}$m
Ans: 9 m

Q. 6 A force of 10 N acting on a body at an angle of 60^∘ with the horizontal direction displaces the body through a distance of 2 m along the surface. Calculate the work done. Now, let the force make an angle of 30^∘ with the horizontal. What is the value of the force to displace the body through 2m along the surface?
Ans: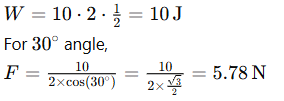$\mathrm{ W}=F\cdot d\cdot \cos (60<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">\circ </sup>)W\; =\; F\; \backslash cdot\; d\; \backslash cdot\; \backslash cos(60^\backslash circ)$

Q. 7 A force of 5 N acting on a body at an angle of 30∘ with the horizontal direction displaces it horizontally through a distance of 6 m. Calculate the work done.
Ans: Work done $W=F\times d\times \cos (30<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">\circ </sup>)W\; =\; F\; \backslash times\; d\; \backslash times\; \backslash cos(30^\backslash circ)$.
$W=5\times 6\times \frac{3}{2}=153\hspace{0.17em}JW\; =\; 5\; \backslash times\; 6\; \backslash times\; \backslash frac\{\backslash sqrt\{3\}\}\{2\}\; =\; 15\backslash sqrt\{3\}\; \backslash ,\; \backslash text\{J\}$J
Ans: $15315\backslash sqrt\{3\}$J

Q. 8 A body of mass 2 kg is moving with a speed of 20 m/s. Find the kinetic energy.
Ans: Kinetic energy $KE=\frac{1}{2}mv\mathrm{<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">2</sup>}$
$KE=\frac{1}{2}\times 2\times \left(20\right)\mathrm{<sup\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">2</sup>}=400\hspace{0.17em}JKE\; =\; \backslash frac\{1\}\{2\}\; \backslash times\; 2\; \backslash times\; (20)^2\; =\; 400\; \backslash ,\; \backslash text\{J\}$J
Ans: 400 J

Q. 9 A moving body of 30 kg has 60 J of KE. Calculate the speed.

Ans: Using $KE=\frac{1}{2}mv2KE\; =\; \backslash frac\{1\}\{2\}\; m\; v^2$, rearrange to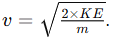  
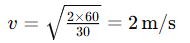A
Ans: 2 m/s

Q. 10 A hammer of mass 1 kg falls freely from a height of 2 m. Calculate (i) the velocity, and (ii) the KE just before it touches the ground.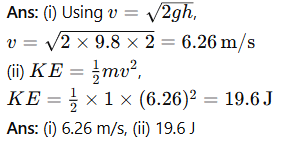

Q. 11 Calculate the energy possessed by a stone of mass 10 kg kept at a height of 5 m. If 196×102J of energy were used to raise a 40 kg boy above the ground, how high would he be raised?
Ans: For the stone, $PE=m\times g\times hPE\; =\; m\; \backslash times\; g\; \backslash times\; h$.
$PE=10\times 9.8\times 5=490\hspace{0.17em}JPE\; =\; 10\; \backslash times\; 9.8\; \backslash times\; 5\; =\; 490\; \backslash ,\; \backslash text\{J\}$J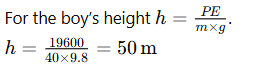

Ans: 490 J for the stone, 50 m for the boy

Q. 12 Calculate the change in velocity required to maintain the same KE if the mass of a body is increased to 4 times its original value.
Ans: To maintain the same KE, the new velocity $v\prime =\frac{v}{2}v\text{'}\; =\; \backslash frac\{v\}\{2\}$ (half the original velocity).
Half the original velocity

Q. 13 A machine does 192 J of work in 240 seconds. What is the power of the machine?
Ans: Power $P=\frac{W}{t}P\; =\; \backslash frac\{W\}\{t\}$.
$P=\frac{192}{240}=0.8\hspace{0.17em}WP\; =\; \backslash frac\{192\}\{240\}\; =\; 0.8\; \backslash ,\; \backslash text\{W\}$W
Ans: 0.8 W

Q. 14 A person weighing 50 kg runs up a hill, rising vertically 10 m in 20 seconds. Calculate power, given $g\; =\; 9.8\; \backslash ,\; \backslash text\{m/s\}^2$g=9.8m/s².
Ans: Power $P=\frac{m}{\times }P\; =\; \backslash frac\{m\; \backslash times\; g\; \backslash times\; h\}\{t\}$.
$P=\frac{50}{\times }=245\hspace{0.17em}WP\; =\; \backslash frac\{50\; \backslash times\; 9.8\; \backslash times\; 10\}\{20\}\; =\; 245\; \backslash ,\; \backslash text\{W\}$W
Ans: 245 W

Q. 15 A rickshaw puller applies a force of 100 N, moving the rickshaw at a constant velocity of 36 km/h. Find the power of the rickshaw puller.
Ans: Convert velocity to m/s: $36\hspace{0.17em}km/h=10\hspace{0.17em}m/s36\; \backslash ,\; \backslash text\{km/h\}\; =\; 10\; \backslash ,\; \backslash text\{m/s\}$m/s.
$P=F\times v=100\times 10=1000\hspace{0.17em}WP\; =\; F\; \backslash times\; v\; =\; 100\; \backslash times\; 10\; =\; 1000\; \backslash ,\; \backslash text\{W\}$W
Ans: 1000 W