Exercise -2.4 : Polynomials, Class 9, Mathematics PDF Download
Exercise -2.4
Q1: Determine which of the following polynomials has (x + 1) a factor :
(i) x3 + x2 + x + 1
(ii) x4 + x3 + x2 + x + 1
(iii) x4 + 3x3 + 3x2 + x + 1
(iv) x3 – x2 – (2 + √2)x + √2
Answer: If (x+1) is a factor of a polynomial p(x), then p(-1) must be equal to zero.
(i)
Let p(x) = x3 + x2 + x + 1
p(-1) = (-1)3 + (-1)2 + (-1) + 1 = -1 + 1 -1 + 1 = 0
∴ (x-1) is a factor of polynomial x3 + x2 + x + 1
(ii)
Let p(x) = x4 + x3 + x2 + x + 1
p(-1) = (-1)4 + (-1)3 + (-1)2 + (-1) + 1 = 1 - 1 + 1 -1 + 1 = 1 ≠ 0
∴ (x-1) is not a factor of this polynomial.
(iii)
Let p(x) = x4 + 3x3 + 3x2 + x + 1
p(-1) = (-1)4 + 3(-1)3 + 3(-1)2 + (-1) + 1
= 1 + 3(-1) + 3(1) -1 + 1 = 1 - 3 + 3 - 1 = 1 ≠ 0
∴ (x-1) is not a factor of this polynomial.
(iv)
Let p(x) = x3 – x2 – (2 + √2)x + √2
p(-1) = (-1)3 – (-1)2 – (2 + √2)(-1) + √2
= -1 - 1 + 2 + √2 + √2 = 2√2 ≠ 0
∴ (x-1) is not a factor of this polynomial.
Q2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1
(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
(iii) p(x) = x3 – 4x2 + x + 6, g(x) = x – 3
Answer:
(i)
p(x) = 2x3 + x2 – 2x – 1, g(x) = x + 1
Zero of x+1 is -1. If g(x) is a factor of p(x) then p(-1) = 0
⇒ p(-1) = 2(-1)3 + (-1)2 – 2(-1) – 1 = -2 + 1 + 2 - 1 = 0
∴ g(x) is a factor of polynomial p(x).
(ii)
p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
Zero of x + 2 is -2. If g(x) is a factor of p(x) then p(-2) = 0
⇒ p(-2) = (-2)3 + 3(-2)2 + 3(-2) + 1 = -8 + 12 - 6 + 1 = -1 ≠ 0
∴ g(x) is not a factor of polynomial p(x).
(iii)
p(x) = x3 – 4x2 + x + 6, g(x) = x – 3
Root of x-2 is 3. If g(x) is a factor of p(x) then p(3) = 0
⇒ p(3) = (3)3 – 4(3)2 + 3 + 6 = 27 - 4(9) + 3 + 6 = 27 - 36 + 3 + 6 = 0
∴ g(x) is a factor of polynomial p(x).
Q3: Find the value of k, if x – 1 is a factor of p(x) in each of the following cases:
(i) p(x) = x2 + x + k
(ii) p(x) = 2x2 + kx + √2
(iii) p(x) = kx2 – √2x + 1
(iv) p(x) = kx2 – 3x + k
Answer:
According to factor theorem, if x -1 is a factor of p(x), then p(1) = 0.
(i) p(x) = x2 + x + k
⇒ p(1) = (1)2 + 1 + k = 0
⇒ 1 + 1 + k = 0
⇒ k = -2
(ii) p(x) = 2x2 + kx + √2
⇒ p(1) = 0
⇒ p(1) = 2(1)2 + k(1) + √2 = 0
⇒ 2 + k + √2 = 0
⇒ k = -2 - √2 = -(2 +√2)
(iii) p(x) = kx2 – √2x + 1
⇒ p(1) = 0
⇒ p(1) = k(1)2 – √2(1) + 1 = 0
⇒ k - √2 + 1
⇒ k = √2 - 1
(iv) p(x) = kx2 – 3x + k
⇒ p(1) = 0
⇒ p(1) = k(1)2 – 3(1) + k = 0
⇒ k - 3 + k = 0
⇒ 2k = 3
⇒ k = 3/2
Q4. Factorise:
(i) 12x2 – 7x + 1
(ii) 2x2 + 7x + 3
(iii) 6x2 + 5x – 6
(iv) 3x2 – x – 4
Answer:
(i) 12x2 – 7x + 1
Method I: By splitting method, let us find out two number p and q such that pq = 12 × 1
and p + q = -7
i.e. p = -4 and q = -3
⇒ = 12x2 – 4x -3x + 1
= 4x(3x - 1) - 1(3x -1)
= (4x -1)(3x -1)
Method II: By factor theorem.
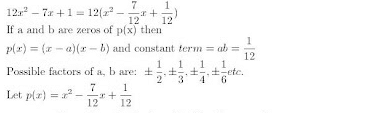

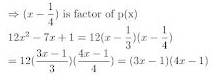
(ii) 2x2 + 7x + 3
Let us find out two number p and q such that pq = 2 × 3 = 6 and p + q = 7
i.e. p = 6 and q = 1
⇒ = 2x2 + 6x + x + 3
= 2x (x + 3) + 1(x + 3)
= (2x + 1)(x + 3) ... answer
(iii) 6x2 + 5x – 6
Let us find out two number p and q such that pq = 6 × -6 = -36 and p + q = 5
i.e. p = 9 and q = -4
∴ 6x2 + 5x – 6 = 6x2 + 9x -4x – 6
= 3x(2x + 3) - 2(2x + 3)
= (2x + 3)(3x - 2) ... answer
(iv) 3x2 – x – 4
Let us find out two number p and q such that pq = 3 × -4 = -12 and p + q = -1
i.e. p = 3 and q = -4
∴ 3x2 – x – 4 = 3x2 + 3x –4x – 4
= 3x(x + 1) -4(x+1)
= (x+1)(3x - 4) ... answer
Q5. Factorise:
(i) x3 – 2x2 – x + 2
(ii) x3 – 3x2 – 9x – 5
(iii) x3 + 13x2 + 32x + 20
Answer:
(i) Let p(x) = x3 – 2x2 – x + 2
Here constant term is 2. Possible factors of 2 are: ±1, ±2
By trial method, p(2) = (2)3 – 2(2)2 – 2 + 2 = 8 - 8 - 2 + 2 = 0
∴ (x -2 ) is factor of p(x).
P(x) ÷ (x -2) =
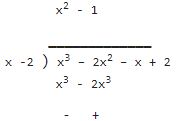
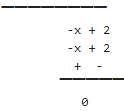
Since, Dividend = Divisor × Quotient + Remainder
∴ x3 – 2x2 – x + 2 = (x-2)(x2 – 1) + 0
= (x - 2)( x2 -x + x– 1)
= (x -2) [x(x-1) + 1 (x-1)]
= (x - 2) (x-1)(x+1)
(ii) Let f(x) = x3 – 3x2 – 9x – 5
Here constant is 5, Possible factors of 5 are ±1 and ±5
By trial method, p(5) = (5)3 – 3(5)2 – 9(5) – 5 = 125 - 75 - 45 - 5 = 0
∴ (x - 5) is factor of polynomial f(x).
Let us find out quotient = f(x) ÷ (x -5)
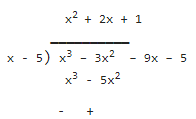
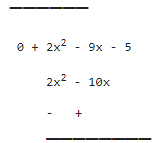
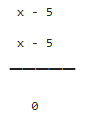
Since, Dividend = Divisor × Quotient + Remainder
∴ x3 – 3x2 – 9x – 5 = (x - 5)(x2 + 2x + 1)
Applying splitting method,
= (x -5)( x2 + x + x + 1)
= (x -5)[x(x+1) +1(x+1)]
= (x-5)(x+1)(x+1)
= (x-5)(x+1)2
Method II:
x3 – 3x2 – 9x – 5 = x3 – 5x2 + 2x2 – 9x – 5
= x2 (x – 5) + 2x2 – 10x + x – 5
= x2 (x – 5) + 2x(x - 5) + 1 (x -5)
= (x - 5)( x2 + 2x + 1)
= (x -5)[x(x+1) +1(x+1)]
= (x-5)(x+1)(x+1)
= (x-5)(x+1)2
(iii) Let p(x) = x3 + 13x2 + 32x + 20
Here constant term is 20. Its factors are: ±1, ±2, ±4, ±5 etc.
By trial method, p(-2) = (-2)3 + 13(-2)2 + 32(-2) + 20
= -8 + 52 -64 + 20 = 0
∴ x + 2 is a factor of polynomial p(x).
⇒ x3 + 13x2 + 32x + 20 = x3 + 2x2 + 11x2+ 22x + 10x + 20
= x2(x + 2) + 11x(x + 2) + 10(x+2)
Taking (x + 2) common, we get
= (x + 2)( x2+ 11x + 10)
(Note: you can use long division method also).
= (x + 2)(x2+ x + 10x + 10)
= (x+2)[x(x+1) + 10(x+1)]
= (x+2)(x+10)(x+1)
FAQs on Exercise -2.4 : Polynomials, Class 9, Mathematics
| 1. What is a polynomial? |  |
| 2. How do we classify polynomials based on their degrees? |  |
| 3. What is the degree of a polynomial? |  |
| 4. Can the degree of a polynomial be negative? |  |
| 5. How do we add or subtract polynomials? |  |















