Exercise 8.2 : Quadrilaterals - Class 9 PDF Download
Exercise 8.2
Q1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is diagonal. Show that:
(i) SR || AC and SR = (1/2) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
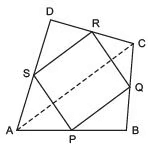
Ans: Given: ABCD is a quadrilateral
To prove: (i) SR || AC and SR = 1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
(i) In ΔADC, S and R are the mid-points of sides AD and CD respectively.
In a triangle, the line segment connecting the midpoints of any two sides is parallel to and half of the third side.
∴ SR || AC and SR = 1/2 AC ... (1)
(ii) In ΔABC, P and Q are mid-points of sides AB and BC respectively. Therefore, by using midpoint theorem,
PQ || AC and PQ = 1/2 AC ... (2)
Using Equations (1) and (2), we obtain
PQ || SR and PQ = SR
(iii) From Equation (3), we obtained
PQ || SR and PQ = SR
Clearly, one pair of quadrilateral PQRS opposing sides is parallel and equal. PQRS is thus a parallelogram.
Q2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Ans: 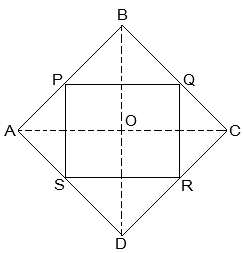
Given: ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
To Prove: PQRS is a rectangle.
Construction:
Join AC and BD.
Proof:
In ΔDRS and ΔBPQ,
DS = BQ (Halves of the opposite sides of the rhombus)
∠SDR = ∠QBP (Opposite angles of the rhombus)
DR = BP (Halves of the opposite sides of the rhombus)
ΔDRS ≅ ΔBPQ [SAS congruency]
RS = PQ [CPCT]———————- (i)
In ΔQCR and ΔSAP,
RC = PA (Halves of the opposite sides of the rhombus)
∠RCQ = ∠PAS (Opposite angles of the rhombus)
CQ = AS (Halves of the opposite sides of the rhombus)
ΔQCR ≅ ΔSAP [SAS congruency]
RQ = SP [CPCT]———————- (ii)
Now,
In ΔCDB,
R and Q are the mid points of CD and BC, respectively.
⇒ QR || BD
also,
P and S are the mid points of AD and AB, respectively.
⇒ PS || BD
⇒ QR || PS
PQRS is a parallelogram.
also, ∠PQR = 90°
Now,
In PQRS,
RS = PQ and RQ = SP from (i) and (ii)
∠Q = 90°
PQRS is a rectangle.
Q3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Ans: 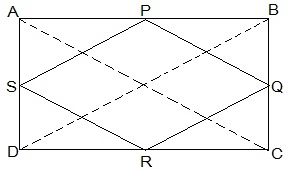 Given: ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively.
Given: ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively.
To prove: The quadrilateral PQRS is a rhombus.
Proof: Let us join AC and BD.
In ΔABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ || AC and PQ = 1/2 AC (Mid-point theorem) ... (1)
Similarly, in ΔADC , SR || AR, SR = 1/2 AC (Mid-point theorem) ... (2)
Clearly, PQ || SR and PQ = SR
It is a parallelogram because one pair of opposing sides of quadrilateral PQRS is equal and parallel to each other.
∴ PS || QR , PS = QR (Opposite sides of parallelogram) ... (3)
In ΔBCD, Q and R are the mid-points of side BC and CD respectively.
∴ QR || BD, QR = 1/2 BD (Mid-point theorem) ... (4)
Also, the diagonals of a rectangle are equal.
∴ AC = BD ... (5)
By using Equations (1), (2), (3), (4), and (5), we obtain
PQ = QR = SR = PS
So, PQRS is a rhombus
Q4. ABCD is a trapezium in which AB || DC , BD is a diagonal and E is the mid - point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
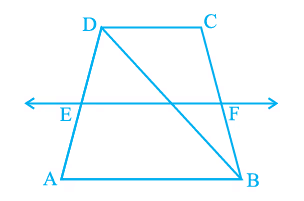
Ans: Given: ABCD is a trapezium in which AB || DC , BD is a diagonal and E is the mid - point of AD. A line is drawn through E parallel to AB intersecting BC at F.
To prove: F is the mid-point of BC.
Proof: Let EF intersect DB at G.
We know that a line traced through the mid-point of any side of a triangle and parallel to another side bisects the third side by the reverse of the mid-point theorem.
In ΔABD, EF || AB and E is the mid-point of AD.
Hence, G will be the mid-point of DB.
As EF || AB, AB || CD,
∴ EF || CD (Two lines parallel to the same line are parallel)
In ΔBCD, GF || CD and G is the mid-point of line BD.
So, by using the converse of mid-point theorem, F is the mid-point of BC.
Q5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
Ans: Given: In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively to prove: The line segments AF and EC trisect the diagonal BD.
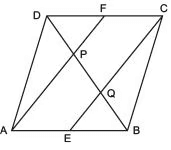
To Prove: The line segments AF and EC trisect the diagonal BD.
Proof: ABCD is a parallelogram.
AB || CD
And hence, AE || FC
Again, AB = CD (Opposite sides of parallelogram ABCD)
1/2 AB = 1/2 CD
AE = FC (E and F are mid-points of side AB and CD)
In quadrilateral AECF, one pair of opposite sides (AE and CF) is parallel and the same as each other. So, AECF is a parallelogram.
∴ AF || EC (Opposite sides of a parallelogram)
In ΔDQC, F is the mid-point of side DC and FP || CQ (as AF || EC ).
So, by using the converse of mid-point theorem, it can be said that P is the mid-point of DQ.
∴ DP= PQ ... (1)
Similarly, in ΔAPB , E is the mid-point of side AB and EQ || AP (as AF || EC ).
As a result, the reverse of the mid-point theorem may be used to say that Q is the mid-point of PB.
∴ PQ = QB ... (2)
From Equations (1) and (2),
DP = PQ= BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Q6. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB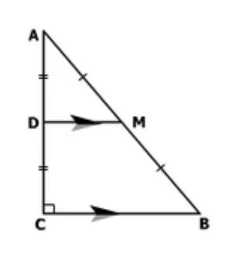 Ans: Given: ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D.
Ans: Given: ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D.
(i) In ΔABC,
It is given that M is the mid-point of AB and MD || BC.
Therefore, D is the mid-point of AC. (Converse of the mid-point theorem)
(ii) As DM || CB and AC is a transversal line for them, therefore,(Co-interior angles)
(iii) Join MC.
In ΔAMD and ΔCMD,
AD = CD (D is the mid-point of side AC)
∠ADM = ∠CDM (Each)
DM = DM (Common)
∴ ΔAMD ≅ ΔCMD (By SAS congruence rule)
Therefore,
AM = CM (By CPCT)
However,
AM = 1/2 AB (M is mid-point of AB)
Therefore, it is said that CM = AM = 1/2 AB.
FAQs on Exercise 8.2 : Quadrilaterals - Class 9
| 1. What are quadrilaterals? |  |
| 2. What are the different types of quadrilaterals? |  |
| 3. How can we identify different types of quadrilaterals? |  |
| 4. What are the properties of a square? |  |
| 5. How can we calculate the area of a quadrilateral? |  |















