Exercise -10.2 & 10.3 - Circles - Class 9 PDF Download
Exercise -10.2
Question 1- 1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer - A circle is a collection of points whose every every point is equidistant from the centre. Thus, two circles can only be congruent when they the distance of every point of the both circle is equal from the centre.

Given,
AB = CD (Equal chords)
To prove,
∠AOB = ∠COD
Proof,
In ΔAOB and ΔCOD,
OA = OC (Radii)
OB = OD (Radii)
AB = CD (Given)
∴ ΔAOB ≅ ΔCOD (SSS congruence condition)
Thus, ∠AOB = ∠COD by CPCT.
Equal chords of congruent circles subtend equal angles at their centres.
Question 2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer
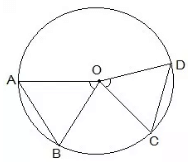
Given,
∠AOB = ∠COD (Equal angles)
To prove,
AB = CD
Proof,
In ΔAOB and ΔCOD,
OA = OC (Radii)
∠AOB = ∠COD (Given)
OB = OD (Radii)
∴ ΔAOB ≅ ΔCOD (SAS congruence condition)
Thus, AB = CD by CPCT.
If chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Exercise -10.3
Question 1- Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
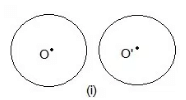
No point is common.
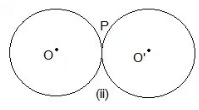
One point P is common.
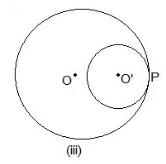
One point P is common.
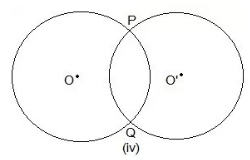
Two points P and Q are common.
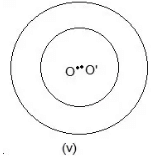
No point is common.
Question 2. Suppose you are given a circle. Give a construction to find its centre.
Answer
Steps of construction:
Step I: A circle is drawn.
Step II: Two chords AB and CD are drawn.
Step III: Perpendicular bisector of the chords AB and CD are drawn.
Step IV: Let these two perpendicular bisector meet at a point. The point of intersection of these two perpendicular
bisector is the centre of the circle.
Question 3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer
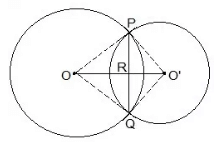
Given,
Two circles which intersect each other at P and Q.
To prove,
OO’ is perpendicular bisector of PQ.
Proof,
In ΔPOO’ and ΔQOO’,
OP = OQ (Radii)
OO’ = OO’ (Common)
O’P = OQ (Radii)
∴ ΔPOO’ ≅ ΔQOO’ (SSS congruence condition)
Thus,
∠POO’ = ∠QOO’ — (i)
In ΔPOR and ΔQOR,
OP = OQ (Radii)
∠POR = ∠QOR (from i)
OR = OR (Common)
∴ ΔPOR ≅ ΔQOR (SAS congruence condition)
Thus,
∠PRO = ∠QRO
also,
∠PRO + ∠QRO = 180°
⇒ ∠PRO = ∠QRO = 180°/2 = 90°
Hence,
OO’ is perpendicular bisector of PQ.
FAQs on Exercise -10.2 & 10.3 - Circles - Class 9
| 1. What is the formula to find the circumference of a circle? |  |
| 2. How is the area of a circle calculated? |  |
| 3. How are the radius and diameter of a circle related? |  |
| 4. Can the circumference of a circle be greater than its diameter? |  |
| 5. Can the area of a circle be negative? |  |















