NCERT Solutions Class 12 Maths Chapter 10 - Vector Algebra
Exercise 10.1
Q1: Represent graphically a displacement of 40 km, 30° east of north.
Ans: 
Here, vector OP represents the displacement of 40 km, 30° East of North.
Q2: Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 metres north-west
(iii) 40°
(iv) 40 watt
(v) 10–19 coulomb
(vi) 20 m/s2
Ans: (i) 10 kg is a scalar quantity because it involves only magnitude.
(ii) 2 meters north-west is a vector quantity as it involves both magnitude and direction.
(iii) 40° is a scalar quantity as it involves only magnitude.
(iv) 40 watts is a scalar quantity as it involves only magnitude.
(v) 10–19 coulomb is a scalar quantity as it involves only magnitude.
(vi) 20 m/s2 is a vector quantity as it involves magnitude as well as direction.
Q3: Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
Ans: (i) Time period is a scalar quantity as it involves only magnitude.
(ii) Distance is a scalar quantity as it involves only magnitude.
(iii) Force is a vector quantity as it involves both magnitude and direction.
(iv) Velocity is a vector quantity as it involves both magnitude as well as direction.
(v) Work done is a scalar quantity as it involves only magnitude.
Question 4: In Figure, identify the following vectors.
 Ans: (i) Vectors a and d are coinitial because they have the same initial point.
Ans: (i) Vectors a and d are coinitial because they have the same initial point.
(ii) Vectors b and d are equal because they have the same magnitude and direction.
(iii) Vectors a and c are collinear but not equal. This is because although they are parallel, their directions are not the same.
Q5: Answer the following as true or false.
(i) a and b are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Ans:
(i) True.
Vectors a and b are parallel to the same line.
(ii) False.
Collinear vectors are those vectors that are parallel to the same line.
(iii) False.
It is not necessary for two vectors having the same magnitude to be parallel to the same line.
(iv) False.
Two vectors are said to be equal if they have the same magnitude and direction, regardless of the positions of their initial points.
Exercise 10.2
Q6: Compute the magnitude of the following vectors: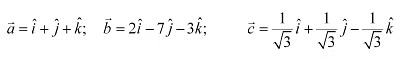
Ans: The given vectors are: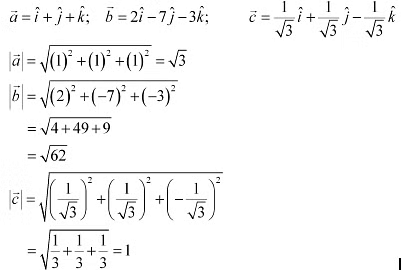
Q7: Write two different vectors having same magnitude.
Ans:
Q8: Write two different vectors having same direction.
Ans: 
Q9: Find the values of x and y so that the vectors  are equal.
are equal.
Ans: The two vectors will be equal if their corresponding components are equal.
Hence, the required values of x and y are 2 and 3 respectively.
Q10: Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
Ans: The vector with the initial point P (2, 1) and terminal point Q (–5, 7) can be given by,
Hence, the required scalar components are –7 and 6 while the vector components are
Q11: Find the sum of the vectors 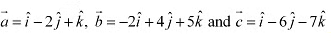

Q12: Find the unit vector in the direction of the vector 
Ans: The unit vector in the direction of vector is given by .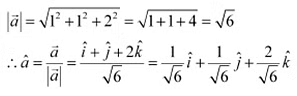
Q13: Find the unit vector in the direction of vector , where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
Ans: The given points are P (1, 2, 3) and Q (4, 5, 6).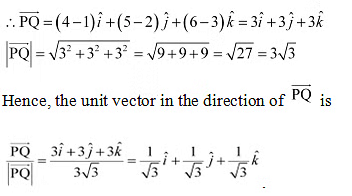
Q14: For given vectors, and , find the unit vector in the direction of the vector
Ans: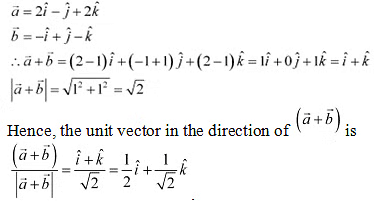
Q15: Find a vector in the direction of vector 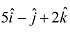
Ans:
Q16: Show that the vectors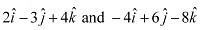 are collinear.
are collinear.
Ans: 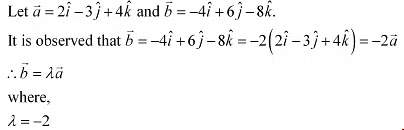
Q17: Find the direction cosines of the vector 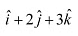
Ans: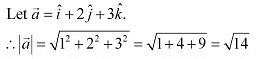
Q18: Find the direction cosines of the vector joining the points A (1, 2, –3) and B (–1, –2, 1) directed from A to B.
Ans: The given points are A (1, 2, –3) and B (–1, –2, 1).
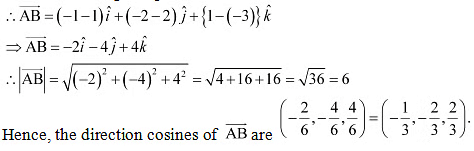
Q19: Show that the vector is equally inclined to the axes OX, OY, and OZ.
Ans: 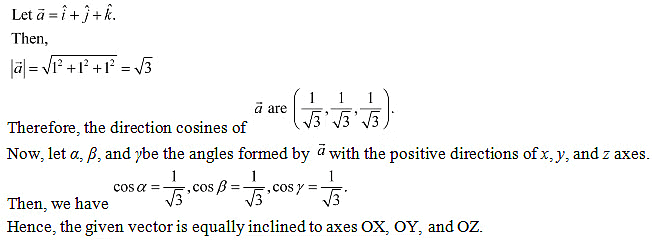
Therefore, the direction cosines of
Now, let α, β, and γbe the angles formed by with the positive directions of x, y, and z axes.
Then, we have
Hence, the given vector is equally inclined to axes OX, OY, and OZ.
Q20: Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are 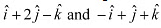 respectively, in the ration 2:1
respectively, in the ration 2:1
Ans: The position vector of point R dividing the line segment joining two points
P and Q in the ratio m: n is given by:
i. Internally:
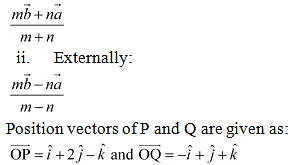
(i) The position vector of point R which divides the line joining two points P and Q internally in the ratio 2:1 is given by,
(ii) The position vector of point R which divides the line joining two points P and Q externally in the ratio 2:1 is given by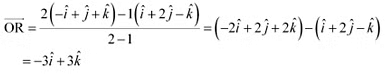
Q21: Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
Ans: The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, – 2) is given by,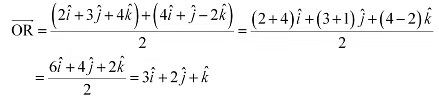
Q22: Show that the points A, B and C with position vectors 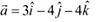 ,
,  respectively form the vertices of a right angled triangle.
respectively form the vertices of a right angled triangle.
Ans: Position vectors of points A, B, and C are respectively given as
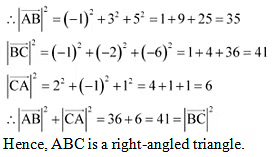
Q23: In triangle ABC which of the following is not true: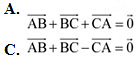
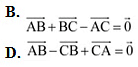
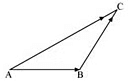
Ans: On applying the triangle law of addition in the given triangle, we have: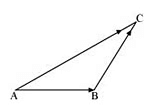

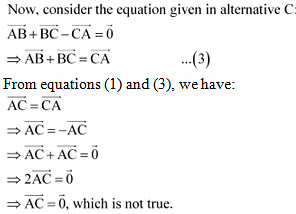
Hence, the equation given in alternative C is incorrect.
The correct answer is C.
Q24: If are two collinear vectors, then which of the following are incorrect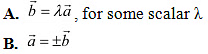
C. the respective components of are proportional
D. both the vectors have same direction, but different magnitudes
Ans: If are two collinear vectors, then they are parallel.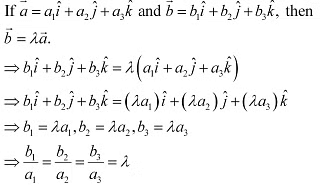
Thus, the respective components of are proportional.
However, vectors can have different directions.
Hence, the statement given in D is incorrect.
The correct answer is D.
Exercise 10.3
Q1: Find the angle between two vectors 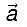 and vector
and vector 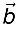 with magnitudes √3 and 2, respectively having
with magnitudes √3 and 2, respectively having 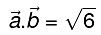
Ans: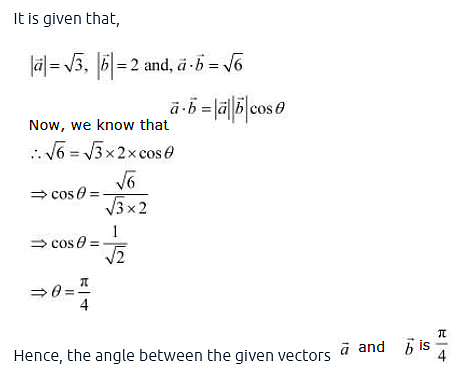 Q2: Find the angle between the vectors
Q2: Find the angle between the vectors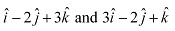 Ans: The given vectors are .
Ans: The given vectors are .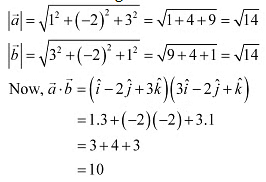
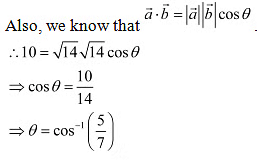 Q3: Find the projection of the vector
Q3: Find the projection of the vector 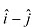 on the vector
on the vector 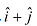 .
. Q4: Find the projection of the vector
Q4: Find the projection of the vector 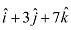 on the vector
on the vector 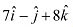 .
. Question 5: Show that each of the given three vectors is a unit vector
Question 5: Show that each of the given three vectors is a unit vector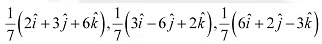
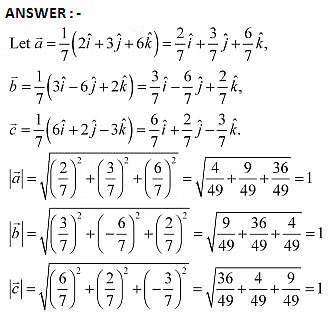
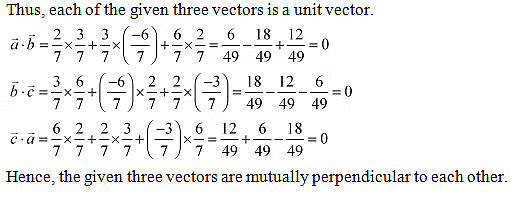 Q6: Find
Q6: Find  , if
, if 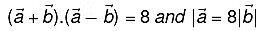
Ans: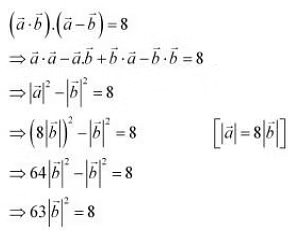
 Q7: Evaluate the product
Q7: Evaluate the product 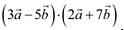 Ans:
Ans: 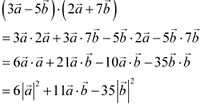 Q8: Find the magnitude of two vectors a and b, having the same magnitude and such that the angle between them is 60° and their scalar product is 1/2.
Q8: Find the magnitude of two vectors a and b, having the same magnitude and such that the angle between them is 60° and their scalar product is 1/2.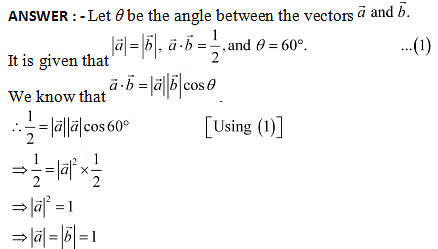 Q9: Find
Q9: Find  , if for a unit
, if for a unit 
Ans: Q10: Show that
Q10: Show that  is perpendicular to
is perpendicular to  ,for any two nonzero vectors a and b.
,for any two nonzero vectors a and b.
Ans: 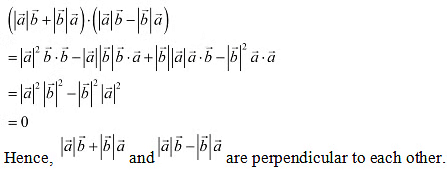 Q11: If , then what can be concluded about the vector ?
Q11: If , then what can be concluded about the vector ?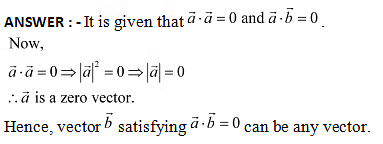 Q12: If
Q12: If  are unit vectors such that
are unit vectors such that 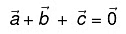 , find the value of
, find the value of 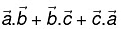
Ans: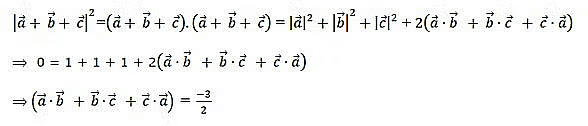 Q13: If either vector a = 0, then b = 0. But the converse need not be true. Justify your answer with an example.
Q13: If either vector a = 0, then b = 0. But the converse need not be true. Justify your answer with an example.
Ans: 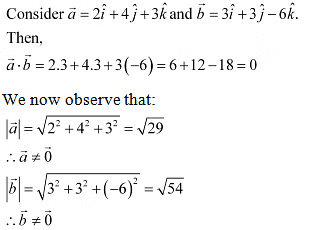 Q14:
Q14: Ans: The vertices of ΔABC are given as A (1, 2, 3), B (–1, 0, 0), and C (0, 1, 2).
Ans: The vertices of ΔABC are given as A (1, 2, 3), B (–1, 0, 0), and C (0, 1, 2). Q15: Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
Q15: Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
Ans: The given points are A (1, 2, 7), B (2, 6, 3), and C (3, 10, –1). Q16: Show that the vectors 2i - j k, i - 3j - 5k and 3i - 4j - 4k form the vertices of a right angled triangle.
Q16: Show that the vectors 2i - j k, i - 3j - 5k and 3i - 4j - 4k form the vertices of a right angled triangle. Q17:
Q17: 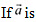 nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then
nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then 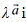 is unit vector if
is unit vector if
(A) λ = 1
(B) λ = –1
(c) a = | λ|
(d) a = 1/| λ|
Ans: Vector  is a unit vector if
is a unit vector if 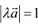
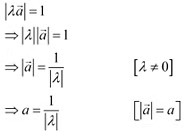

|
204 videos|290 docs|139 tests
|
FAQs on NCERT Solutions Class 12 Maths Chapter 10 - Vector Algebra
| 1. What are the basic concepts of vector algebra? |  |
| 2. How is vector algebra used in physics and engineering? |  |
| 3. What is the significance of vector algebra in computer graphics? |  |
| 4. How can one determine the angle between two vectors using vector algebra? |  |
| 5. Can vector algebra be used to solve real-world problems? |  |

|
Explore Courses for JEE exam
|

|


















