Kinematics :
1. Rest and Motion :
* An object is said to be in motion wrt a frame of reference S1, when its location is changing with time in same frame of reference S1.
 Fig: An object at rest.* Rest and motion are relative terms.
Fig: An object at rest.* Rest and motion are relative terms.
* Absolute rest and absolute motion have no meaning.
Motion is broadly classified into 3 categories :
1. Rectilinear and translatory motion.
2. Circular and rotatory motion.
 Fig: Example of circular motion.
Fig: Example of circular motion.
3. Oscillatory and vibratory motion.
1.1 Rectilinear or 1-D Motion :
When a particle is moving along a straight line, then its motion is a rectilinear motion.
 Fig: Example of rectilinear motion.Parameters of rectilinear motion or translatory motion or plane motion :
Fig: Example of rectilinear motion.Parameters of rectilinear motion or translatory motion or plane motion :
(A) Time :
* It is a scalar quantity and its SI unit is second(s).
* At a particular instant of time, a physical object can be present at one location only.
* Time can never decrease.
(B) Position or location : It is defined with respect to some reference point (origin) of given frame of reference.
Consider a particle which moves from location  (at time t1) to location
(at time t1) to location  (at time t2) as shown in the figure below,
(at time t2) as shown in the figure below,

following path ACB.
(C) Distance :
The length of the actual path traversed by the particle is termed as its distance.
Distance = length of path ACB.
* Its SI unit is metre and it is a scalar quantity.
* It can never decrease with time.
(D) Displacement :
The change in position vector of the particle for a given time interval is known as its displacement.

* Displacement is a vector quantity and its SI unit is metre.
* It can decrease with time.
For a moving particle in a given interval of time :
* Displacement can be +ve, -ve or 0, but distance would be always +ve.
* Distance > Magnitude of displacement.
* Distance is always equal to displacement only and only if particle is moving along a straight line without any change in direction.
(E) Average speed and average velocity :
Average speed and average velocity are always defined for a time interval.


* Average speed is a scalar quantity, while average velocity is a vector quantity. Both have the same SI units, i.e., m/s.
For a moving particle in a given interval of time :
* Average speed can be a many valued function but average velocity would be always a single-valued function.
* Average velocity can be positive, negative or 0 but average speed would be always positive.
(F) Instantaneous speed and instantaneous velocity :
Instantaneous speed is also defined exactly like average speed i.e. it is equal to the ratio of total distance and time interval, but with one qualification that time interval is extremely (infinitesimally) small. The instantaneous speed is the speed at a particular instant of time and may have entirly different value than that of average speed. Mathematically.
 ...(4)
...(4)
When Ds is the distance travelled in time Dt.
As Dt tends to zero, the ratio defining speed becomes finite and equals to the first derivative of the distance. The speed at the moment 't' is is called the instantaneous speed at time 't'.
 On the distance - time plot, the speed is equal to the slope of the tangent to the curve at the time instant 't'. Let A and B point on the plot corresponds to the time t and t + Dt during the motion. As Dt approaches zero, the chord AB becomes the tangent AC at A. The slope of the tangent equal ds/dt, which is equal to the intantaneous speed at 't'.
On the distance - time plot, the speed is equal to the slope of the tangent to the curve at the time instant 't'. Let A and B point on the plot corresponds to the time t and t + Dt during the motion. As Dt approaches zero, the chord AB becomes the tangent AC at A. The slope of the tangent equal ds/dt, which is equal to the intantaneous speed at 't'.
v = tanq =  =
= 
(G) Instantaneous velocity :
Instantaneous velocity is defined exactly like speed. It is equal to the ratio of total displacement and time interval, but with one qualification that time interval is extremely (infinitesimally) small. Thus, instantaneous velocity can be termed as the average velocity at a particular instant of time when Dt tend to zero and may have entirely different value that of average velocity, Mathematically.

As Dt tends to zero, the ratio defining velocity becomes finite and equals to the first derivative of the position vector. The velocity at the moment 't' is called the instantaneous velocity or simply velocity at time 't'.

 The magnitude of average velocity |vavg| and average speed vavg may not be equal, but magnitude of instantaneous velocity |v| is always equal to instantaneous speed v.
The magnitude of average velocity |vavg| and average speed vavg may not be equal, but magnitude of instantaneous velocity |v| is always equal to instantaneous speed v.
Ex. 1: In 1.0 sec a particle goes from point A to point B moving in a semicircle of radius 1.0 m. The magnitude of average velocity is
(A) 3.14 m/sec
(B) 2.0 m/sec
(C) 1.0 m/sec
(D) zero
Sol.

D = AO + OB
= 1 + 1 = 2m
t = 1 sec (given)
⇒ mg of v of  = 2m/sec
= 2m/sec
Ex. 2: A particle moves along a semicircular path of radius R in time t with constant speed. For the particle calculate

(i) distance travelled,
(ii) displacement,
(iii) average speed,
(iv) average velocity.
Sol.
(i) Distance = length of path of particle =  = πR
= πR
(ii) Displacement = minimum distance between initial and final point
= AB = 2R
(iii) Average speed, v =  =
= 
(iv) Average velocity = 
Ex. 3: A body travels the first half of the total distance with velocity v1 and the second half with velocity v2. Calculate the average velocity :
Sol. Let total distance = 2x. Then
total time taken =  = x
= x 
 Average speed =
Average speed =  =
= 
(G-1) When velocity is given as a function of t :
Ex. 4: Velocity-time equation of a particle moving in a straight line is,
v = (10 + 2t + 3t2)
Find :
(a) displacement of particle from the origin of time t = 1 s, if it is given that displacement is 20 m at time t = 0
(b) acceleration-time equation.
Sol.
(a) The given equation can be written as,
v = 
ds = (10 2t 3t2) dt
or  or s - 20 = [10t + t2 + t3]01
or s - 20 = [10t + t2 + t3]01
or s = 20 + 12 = 32 m
(b) Acceleration-time equation can be obtained by differentiating the given equation w.r.t. time.
Thus,=
a =  =
=  or a = 2 + 6t
or a = 2 + 6t
Specimen problem :
(A) When equation of displacement is given and speed to be find out :
Ex. 5: If displacement is depend on time such that x = 2t -2 then find out average speed upto 4 sec.
Sol. Average speed = 
for Total distance
at t = 0 it is at x = - 2
at t = 1 it is at 0 m
at t = 4 it is at 6 m.
Total distance = |- 2| + 0 + 6 = 8 m
Average speed = 8/4 = 2m/sec
(B) When velocity is given as a function of time and distance to be find out :
In this type of question first find out at what instant the velocity is zero. If this instant is come in our time limit then distance can be calculated by breaking the integration in two part with modulas.
Ex. 6: If velocity is depend on time such that v = 4 - 2t. Find out distance travelled by particle from 1 to 3 sec.
Sol. Velocity is zero (4 - 2t = 0) at t = 2 sec
So for distance  = 4 - 2t ⇒ dx =
= 4 - 2t ⇒ dx =  +
+ 
dx = 1 + 1 = 2m
(G-2) When velocity is given as a function of x :
v = f(x) ⇒  ⇒
⇒ 
Ex. 7: If velocity is given by following function V = x2. Then find out relation between x & t (assume x = 1 m at t = 0)
Sol. Relation between v & x is
v = x2
we know that v =  ⇒
⇒ 
 ⇒
⇒  ⇒
⇒ 
⇒ -  + 1 = t ⇒ x =
+ 1 = t ⇒ x = 
(E) Average and instantaneous acceleration :
When the velocity of a moving object/particle changes with time, we can say that it is accelerated.
Average acceleration,

Instantaneous acceleration,
 = Rate of change of velocity
= Rate of change of velocity
Acceleration is a vector quantity whose direction is same as that of change in velocity vector. Its SI unit is m/s2.
* When direction of acceleration and velocity are opposite to each other, then acceleration is termed as retardation.
*
(E-1) When acceleration is given as a function of x :
Ex. 8: if a = 2x ; initially particle is at x = 2m and is moving with 3 ms-1. Then find out v at x = 5 m.
Sol. Given a = 2x
⇒  ⇒
⇒ 
⇒  = 25 - 4 ⇒ v2 - 9 = 21 × 2 ⇒ v =
= 25 - 4 ⇒ v2 - 9 = 21 × 2 ⇒ v = 
(E-2) When acceleration is given as function of velocity :
Ex. 9: If a is depend on v in a following way.
a = v and at t = 0 x = 1m, v = 1m/s.
(a) Find out its velocity at t = 2 sec.
(b) Find out its velocity at x = 3 m
Sol.
(a) Given a = v
⇒  ⇒
⇒ 
⇒ ln v = 2 ⇒ v = e2 ms-1
(b) Given a = v
⇒  ⇒
⇒ 
⇒ v - 1 = 2 ⇒ v = 3 ms-1
(E-3) When acceleration is given as a function of t :
Ex. 10: The acceleration of a particle which is depend on time is given by following function
a = 2t + 1
and at time t = 0, x = 1m and ui = 2m/s.
Then find out displacement of the particle at t = 3 sec.
Sol.  We know that a =
We know that a =  ⇒ = 2t + 1 ⇒ dv = (2t + 1) dt
⇒ = 2t + 1 ⇒ dv = (2t + 1) dt
 =
= 
vf - 2 = t2 + t ⇒ vf = t2 + t + 2
Now v = 
⇒  = t2 + t + 2 ⇒
= t2 + t + 2 ⇒ 
xf = 
So, xf at t = 3 sec is
=  ⇒ 20.5 m
⇒ 20.5 m
So, after t = 3 sec the position of the particle is 20.5m but the displacement of the particle is
= 20.5 - 1 = 19.5 m
(E-4) Constant Acceleration Format :
Deduce the following equations for unifromly accelerated motion by using intergration technique.
(A) v = u +at (B) s = ut +  at2
at2
(C) v2 - u2 = 2as (D) snth = u + (2n - 1)
(2n - 1)
First equation of motion :
Acceleration is defined as :

or dv = adt ...(1)
When time = 0, velocity = u (say)
When time = t, velocity = v (say)
Integrating equation (1) within the above limits of time and velocity, we get
 or
or 
or v - u = a(t - 0)
or v = u + at ...(2)
Second equation of motion Velocity is defined as :

or ds = v dt = (u + at) dt ...(iii)
When time = 0, displacement travelled = 0
When time = t, displacement travelled = s (say).
Integrating equation (3) within the above limits of time and distance, we get
 or
or 

Third equation of motion :
By the definitions of acceleration and velocity,

or ads = vdv ...(5)
When time = 0, velocity = u, displacement travelled = 0
When time = t, velocity = v, displacement travelled = s
(say)
Integrating equation (5) within the above limits of velocity and displacement, we get
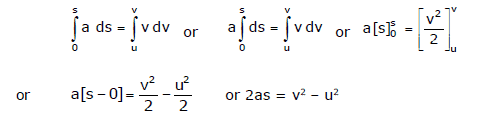
or v2 - u2 = 2as ...(6)
Fourth equation of motion :
By definition of velocity,

or ds = vdt = (u + at) dt ...(7)
When time = (n - 1) second, displacement travelled
= sn - 1 (say).
When time = n second, displacement travelled = sn
(say)
Integrating equation (7) within the above limits of time and distance, we get

Ex. 11: A car starts from rest and accelerates uniformly for 20 seconds to a velocity of 72 km h-1. It then runs at constant velocity and finally brought to rest in 200 m with a constant retardation. The total distance covered is 600 m. Find the acceleration, retardation and the total time taken.
Sol.
(i) Motion with uniform acceleration :
Here, u = 0 ; t1 = 20 sec ; v = 72 ×  = 20 ms-1
= 20 ms-1
 v = u + at1
v = u + at1
20 = 0 + a × 20 or a = 1 m s-2
Distance travelled by car in this time (20 sec),
S1 = ut +  = 0 +
= 0 +  × 1 × (20)2 = 200 m
× 1 × (20)2 = 200 m
(ii) Motion with uniform velocity :
As given, total distance = 600 m
we have calculated S1 = 200 m (with uniform acc.)
and S2 = 200 m (with retardation)
 Net distance for which body moves with uniform velocity,
Net distance for which body moves with uniform velocity,
S = 600 - S1 - S2
= 600 - 200 - 200 = 200 m


 Total time of journey, t = (20 + 10 + 20) sec
Total time of journey, t = (20 + 10 + 20) sec
t = 50 sec
Average velocity =  = 12 m/s.
= 12 m/s.
(iii) Motion with uniform retardation :
For this motion, initial velocity, u = 20 m s-1 and final velocity v = 0 ; S2 = 200 m
Acceleration a' = ?
Using, v2 - u2 = 2 a' S2
(0)2 - (20)2 = 2(a') × 200
a' = - 1 ms-2
Let = time for which the body comes to rest.
 v = u a' t'
v = u a' t'
0 = 20 - 1t'
 t' = 20 sec.
t' = 20 sec.
C. Specimen Problem :
Ex. 12: Find out distance travelled by the block in 10 sec. for a given situation.

Sol. First find out it what instant velocity of block becomes zero.
v = u + at
given : u = 10 m/s, a = - 2m/s2
⇒ 0 = 10 - 2t ⇒ t = 5 sec
So we calculate distance for two time intervals.
For first 5 sec.
S1 = ut -  at2 ⇒ S1 = (10)(5) -
at2 ⇒ S1 = (10)(5) -  (2) (5)2 = 25 m
(2) (5)2 = 25 m
for Next 5 sec (block is travelling towards the starting point)
S2 = ut + at2
at2
u = 0
S2 =  × 2 × 25 = 25 m
× 2 × 25 = 25 m
S = S1 + S2 = 50 m
(D) Reaction time :
When a particular situation demands our immediate action, it takes some time before we really respond. Reaction time is the time a person takes to observe, think and act. For example, if a person is driving and suddenly a boy appears on the road, then the time elapse before he applies the breaks of the car is the reaction time. Reaction time depends on complexity of the situation and on an individiual.
One can measure one's reaction time by a simple experiment. Take a rule and ask your friend to drop it vertically through the gap between your thumb and forefinger. As soon as it is dropped, note the time elapsed ts before you catch it and the distance d travelled by the ruler. (In a particular case, y was found to be 21.0 cm. Estimate reaction time).
Sol. As the ruler drops under free fall so u = 0, and g = 9.8 ms-2. The distance travelled d and the reaction time tr are related by
 Or,
Or, 
Here d = 21.0 cm = 0.21 m

Note :
Definition : Time taken by a driver to react for a situation

Reaction Time of the driver is Δt = t1 - t0
Total distance covered by the car before stopping
= distance covered in uniform motion during to to t1 + distance
cover in deaccelerated motion during t1 to t2 = Total distance = u(Δt) + 
Ex. 13: Assume that a car is able to stop with a retardation of 8 ms-2 and that a driver can react to an emergency in 0.5 sec. Calculate the overall stopping distance of the car for a speed of 60 km-1 of the car.
Sol. Here, u = 60 km h-1
Since the application of brakes takes 0.5 s, before this the car was moving with uniform speed of  .
.
 Distance covered in 0.5 sec, with a uniform speed is
Distance covered in 0.5 sec, with a uniform speed is

Now car begins to move with a retardation of 8ms-2
 Distance covered before coming to rest,
Distance covered before coming to rest,
2a S2 = v2 - u2
or 

 Total (overall) distance = S1 + S2 = 8.33 + 17.36 ⇒ S = 25.69 m
Total (overall) distance = S1 + S2 = 8.33 + 17.36 ⇒ S = 25.69 m
Ex. 14: Two buses A and B are at positions 50 m and 100 m from the origin at time t = 0. They start moving in the same direction simultaneously with uniform velocity of 10 ms-1 and 5 ms-1. Determine the time and postion at which A overtakes B.
Sol. Here we use equation of motion for constant velocity in Cartesian form.
Given x1 (0) = 50 m, x2 (0) = 100 m,
v1 = 10 ms-1, v2 = 5 ms-1
The positions of the two buses at any instant t are
x1 (t) = x1 (0) + v1t = 50 + 10 t
x2 (t) = x2 (0) + v2t = 100 + 10 t
When A overtakes B,
x1 (t) = x2 (t)
50 + 10t = 100 + 5t or 5t = 50
t = 10 s
x1 (10) = x2 (10) = 150 m
Thus A overtakes B at a position of 150 m from the origin at time t = 10 s.
Ex. 15: A bus starts from rest with constant acceleration of 5 ms-2. At the same time a car travelling with a constant velocity of 50 ms-1 overtakes and passes the bus.
(i) Find at what distance will the bus overtake the car ?
(ii) How fast will the bus be travelling then ?
Sol.
(i) Suppose the bus overtakes the car after covering distance s.
When the two meet, time taken t is same.
For bus, 
For car, s = 50 t
 or t = 20 s
or t = 20 s
Hence s = 50 t = 50 × 20 = 1000 m.
(ii) v2 = u2 + 2as = 0 + 2 × 5 × 1000 = 10,000 or v = 100 ms-1
Specimen problem :
(E) Maximum Separation :
Ex. 16: 

What is the maximum separation between car and scooter ?
Sol. Initially seperation between car & scooter increases and then decreases.
Separation between them will be maximum at an instant at which velocity of the car is equal to the velocity of scooter.
Velocity car = Velocity scooter = 40 m/s
from v = u + at
40 = 0 + 4t ⇒ t = 10 sec
The distance travelled by scooter in 10 sec.
is S1 = 10 × 40 = 400 m
The distance travelled by car in 10 sec. is
S2 = ut +  = 0 × 4 × (10)2 = 200 m
= 0 × 4 × (10)2 = 200 m
So maximum seperation = S1 - S2 = 400 - 200 = 200 m
* When they meet both will travel the same distance.
 Questions 14, 15, 16 can be solved in a relatively easier way using the concept of relative motion which is explained later
Questions 14, 15, 16 can be solved in a relatively easier way using the concept of relative motion which is explained later
 Now you can try Questions 1 to 13 in Ex. 1 and 1 to 6 in Exercise II
Now you can try Questions 1 to 13 in Ex. 1 and 1 to 6 in Exercise II
2. Motion under gravity :
I format (When a body is thrown vertically upward) :
It includes two types of motion
(i) De-accelerated motion from A to B because the direction of velocity and acceleration is opposite. So speed decreases.
(ii) Accelerated motion from B to C because the direction of velocity and acceleration is same (downward). So speed increases.
 Fig: Motion of an object under gravity.(a) Time of flight :
Fig: Motion of an object under gravity.(a) Time of flight :
It is the time taken by the particle to reach the ground. If the particle is thrown vertically upward with initial velocity u then
ui = u
a = - g (take downward direction negative)
from equation
S = ut +  ⇒ Snet = 0 (when particle again reaches the ground)
⇒ Snet = 0 (when particle again reaches the ground)
t = T (time of flight)
0 = uT -  ⇒ T =
⇒ T = 
(b) Maximum Height :
from v2 = u2 + 2as
at maximum height v = 0, s = Hmax
⇒ 0 = u2 -2 gHmax ⇒ Hmax = 
(c) Final velocity :
from v = u + at
v = vf a = - g t = T =  ⇒ vf = u - g
⇒ vf = u - g 
vf = - u
i.e. the body reaches the ground with the same speed with which it was thrown vertically upwards as it thrown vertically upward.
(d) Time to reach half of the maximum height :

ui = u a = - g
from S = ut + 
 = ut -
= ut - 
H = 2ut - gt2 ⇒ gt2 - 2ut + H = 0
⇒ t =  ⇒ t =
⇒ t = 

t =  ...(1)
...(1)
Equation 1 gives two value of time which corresponds to
t1 =  (from ground to Hmax/2 in upward motion)
(from ground to Hmax/2 in upward motion)
t2 =  (from ground to Hmax/2 in downward motion)
(from ground to Hmax/2 in downward motion)
(e) Time to reach any general height h :

Let us assume that particle reaches from A to B in time t1 & from A to C is time t2.
So from S = ut +  ⇒ h = ut -
⇒ h = ut - 
gt2 - 2ut + 2h = 0
⇒ t = 
So, t1 =  , t2 =
, t2 = 
⇒ t1 + t2 = T (Time of flight)
II Format (Free fall) :
A body released near the surface of the earth is accelerated downward under the influence of force of gravity.
(a) Time of Flight :

from equation S = ut + 
S = - H, u = 0, a = - g
t = T (Let assume)
⇒ - H = (0)T -  ⇒ T =
⇒ T = 
(b) Final Velocity when body reaches the ground :
from v2 - u2 = 2as
s = - H v = vf u = 0 a = - g
⇒  - 0 = 2 (-g) (-H) ⇒ vf =
- 0 = 2 (-g) (-H) ⇒ vf = 
Ex. 17: A ball is thrown vertically upwards with a velocity u from the ground. The ball attains a maximum height Hmax. Then find out the time and displacement at which ball have half of the maximum speed.
Sol. Maximum speed of the ball is u
At point B and C ball have speed u/2 but direction
is opposite so from,
v = u + at

Let t1 is the time taken by the ball from point A to B and t2 is the time taken by the ball from A to C
From A to B  ...(i)
...(i)
From A to C  ....(2)
....(2)
from (i) t1 =  , from (ii) t2 =
, from (ii) t2 = 
from equation v2 - u2 = 2as
⇒ v = ± u/2, u = u, a = - g ⇒  = - 2gh
= - 2gh
h = 

 h =
h = 
Ex. 18: A ball thrown vertically upwards with a speed of 19.6 ms-1 from the top of a tower returns to the earth in 6 s. Find the height of the tower.
Sol. Here u = 19.6 ms-1
g = -9.8 ms-2
Net displacement, s = - h
Negative sign is taken because displacement is in the opposite direction of initial velocity.
As s = ut + 
 - h = 19.6 × 6
- h = 19.6 × 6  × (-9.8) × 62
× (-9.8) × 62
= 117.6 - 176.4 = -58.8
or h = 58.8 m
Ex. 19: A ball is thrown vertically upwards with a velocity of 20 ms-1 from the top of a multi-storeyed building. The height of the point from where the ball is thrown is 25 m from the ground.
(i) How high will the ball rise and
(ii) how long will it be before the ball hits the ground?
Sol. (i) Here u = +20 ms-1, g = -10 ms-2
At the highest point, v = 0
Suppose the ball rises to the height h from the point of projection.
As v2 - u2 = 2gs
 02 - 202 = 2 × (-10) × h or h = +20 m.
02 - 202 = 2 × (-10) × h or h = +20 m.
(ii) Net displacement, s = -25 m
Negative sign is taken because displacement is in the opposite direction of initial velocity.
As s = ut + 
 -25 = 20t +
-25 = 20t +  × (-10) × t2
× (-10) × t2
or 5t2 - 20t - 25 = 0 or t2 - 4t - 5 = 0
or (t + 1) (t - 5) = 0
As t ¹ -1, so t = 5s.
Ex. 20: A ball thrown up is caught by the thrower after 4s. How high did it go and with what velocity was it thrown ? How far was it below the highest point 3 s after it was thrown?
Sol. As time of ascent = time of descent
 Time taken by the ball to reach the highest point = 2 s
Time taken by the ball to reach the highest point = 2 s
For upward motion of the ball : u = ?, v = 0, t = 2s, g = - 9.8 ms-2
As v = u + gt
 0 = u - 9.8 × 2
0 = u - 9.8 × 2
or u = 19.6 ms-1
Maximum height attained by the ball is given by
s = ut +  = 19.6 × 2 +
= 19.6 × 2 +  × (9.8) × 22 = 19.6 m.
× (9.8) × 22 = 19.6 m.
Displacement of the ball in 3 s,
s = 19.6 × 3 +  × (-9.8) × 32 = 58.8 - 44.1 = 14.7 m
× (-9.8) × 32 = 58.8 - 44.1 = 14.7 m
Distance of the ball from the highest point 3 s after it was thrown
= 19.6 - 14.7 = 4.9 m.
Ex. 21: A balloon is ascending at the rate of 9.8 ms-1 at a height of 39.2 m above the ground when a food packet is dropped from the balloon. After how much time and with what velocity does it reach the ground?
Take g = 9.8 ms-2.
Sol. Initially the food packet attains the upward velocity of the balloon, so
u = 9.8 ms-1, g = 9.8 ms-2 , s = -39.2 m
Here s is taken negative because it is in the opposite direction of initial velocity.
Using, s = ut +  , we get
, we get
- 39.2 = 9.8 t -  × 9.8 t2
× 9.8 t2
or 4.9 t2 - 9.8 t - 39.2 = 0 or t2 - 2t - 8 =0
or (t - 4) (t 2) = 0 or t = 4 s or - 2 s
As time is never negative, so t = 4s.
Velocity with which the food packet reaches the ground is
v = u + gt = 9.8 - 9.8 × 4 = - 29.4 ms-1.
Negative sign shows that the velocity is directed vertically downwards.
 When a particle is dropped then it will automatically attains the velocity of the frame at that time.
When a particle is dropped then it will automatically attains the velocity of the frame at that time.
Ex. 22: Two balls are thrown simultaneously, A vertically upwards with a speed of 20 ms-1 from the ground, and B vertically downwards from a height of 40 m with the same speed and along the same line of motion. At what points do the two balls collide? Take g = 9.8 ms-2.
Sol. Suppose the two balls meet at a height of x from the ground after time t s from the start.

For upward motion of balls A :
u = 20 ms-1, g = - 9.8 ms-2
s = ut +
x = 20 t -  × 9.8 t2 = 20t - 4.9 t2 ...(i)
× 9.8 t2 = 20t - 4.9 t2 ...(i)
For downward motion of ball B,
40 - x = 20 × t+  × 9.8 t2
× 9.8 t2
= 20t + 4.9 t2 ... (ii)
Adding (i) and (ii), 40 = 40 t or t = 1 s
From (i), x = 20 × 1 - 4.9 × (1)2 = 15.1 m
Hence the two balls will collide after 1 s at a height of 15.1 m from the ground.
3. Graphs :
(i) Straight line : A linear relation between y & x represents a straight line.
General equation of straight line

y = mx + c
m is the slope of line
c is the y intercept i.e. where the line cuts the y-axis. Slope is defined as the tan of angle made by the straight line with positive x-axis in anticlockwise direction.
m < 0 ⇒ q > 90°
m > 0 ⇒ q < 90°
0° £ q < 180°
Ex. 23: Draw the graph for the equation : 2y = 3x + 2
Sol. 2y = 3x + 2 ⇒ y = 

m =  > 0 ⇒ q < 90°
> 0 ⇒ q < 90°
c = +1 > 0
⇒ The line will pass through (0, 1)
Ex. 24: Draw the graph for the equation : 2y + 4x + 2 = 0
Sol. 2y + 4x + 2 = 0 ⇒ y = - 2x - 1

m = - 2 < 0 i.e., q > 90°
c = - 1 i.e.,
line will pass through (0, -1)
 : (i) If c = 0 line will pass through origin.
: (i) If c = 0 line will pass through origin.
(ii) y = c will be a line parallel to x axis.
(iii) x = c will be a line perpendicular to y axis

(ii) Parabola :
A general quadratic equation represents a parabola.
y = ax2 + bx +c a = 0
if a > 0 ; It will be a opening upwards parabola.
if a < 0 ; It will be a opening downwards parabola.
if c = 0 ; It will pass through origin.
e.g. y = 4 x2 + 3x 
Average velocity & instantaneous velocity from position vs time graph : Average velocity from t1 to t2
=  =
= 
=  = slope of the chord AB
= slope of the chord AB

vinstantaneous = 
when t2 approaches t1 point B approaches point A and the chord AB becomes tangent to the curve. Therefore
vinstantaneous = Slope of the tangent x - t curve
(iii) Reading of Graph :
(A) Reading x v/s t graphs Explanation :
(1)

Body is at rest at x0.
(2)

Body starts from origin and is moving with speed tan q away from origin.
(3)

Body starts from rest from origin and moves away from origin with increasing speed velocity and positive acceleration.
(4)

Body starts from rest from x = x0 and moves away from origin with increasing velocity or ve acceleration.
(5)
Body starts from x = x0 and is moving toward the origin with constant velocity passes throw origin after same time and continues to move away from origin.
(6)
Body starts from rest at x = x0 and then moves with increasing speed towards origin
 acceleration is -ve
acceleration is -ve
(7) Body starts moving away from origin with some initial speed. Speed of body is decreasing till t1 and it becomes 0 momentarily of t = t1 and At this instant. Its reverses its direction and move towards the origin with increasing speed.
(8)

Body starts from origin moves away from origin in the -ve x-axis at t = t1 with decreasing speed and at t= t1 it comes at rest momentarily, Reverses its direction moves towards the origin the increasing speed. Crosses the origin at t = t2.
(9)
Body starts from origin from rest and moves away from origin with increasing
speed.
(B) V-t Graphs :
(1)

Body is always at rest.
(2)

Body is moving with constant velocity v0
(3)

Body is at rest initially then it starts moving with its velocity increasing at a
constant rate i.e. body is moving with constant acceleration.
(4)

Body starts its motion with initial velocity v0 and continues to move with its velocity increasing at a constant rate i.e. acceleration of the body is constant.
(5)

Body starts its motion with initial velocity v0. Then it continues to move with its velocity decreasing at a constant rate i.e. acceleration of the body is negative and constant. At t = t0 the body comes to rest instantaneously and reverses its direction of motion and then continues to move with decreasing velocity or increasing speed.
For 0 < t < t0 motion of the body is deaccelerated ( speed is decreassing)
speed is decreassing)
t > t0 motion of the body is accelerated ( speed is increasing)
speed is increasing)
(6)

Body is at rest initially. Then it starts moving with increasing velocity. As time increases its velocity is increasing more rapidly. i.e. the moving with increasing acceleration.
(7)

Body starts its motion with initial velocity v0. Its velocity is decreasing with time and at t = t0 . It becomes zero after body reverse its direction of motion and continues to move with decreasing velocity or increasing speed. Since velocity of the body is decreasing for whole motion. Therefore, its acceleration is negative.For 0 < t < t0 motion of the body is deaccelerated (speed is decreasing) t > t0 motion of the body is accelerated (Q speed is increasing).
(C) Reading of a - t Graphs :
(1) 
acceleration of the body is zero that means the body is moving constant velocity.
(2)

Acceleration of the body is constant and positive.
(3)

Acceleration of the body is constant and negative
(4)

Initially the acceleration of the body is zero. Then its acceleration is increasing
at a constant rate.
(5)

The body starts accelerating(initial acceleration zero) at t = 0. Its acceleration is
negative for whole of its motion and is decreasing at a constant rate.
(6)

Initially acceleration of the body is zero. Its acceleration is positive for whole of its motion. Its acceleration is increasing for whole of its motion.
(IV) Drawing of graphs on the basis of given information :
(a) If acceleration of the body is zero :
(i) If the velocity of the body is v0 and it starts from origin :


(ii) If at t = 0, x = x0 then :


(iii) If at t = 0, x = - x0 then :


(b) If a body has constant acceleration :
For this section :
(i) u0, x0 & a0 are positive constants.
(ii) u º = initial velocity.
(iii) v º = velocity at any time t.
(iv) x º = position at any time t.
xi º = initial position
(i) if u = 0, a = a0





v = a0t
(ii) If u = u0 , a = a0
x = xi + u0t  v = u0 + a0t
v = u0 + a0t




(iii) if u = u0, a = - a0
x = xi + u0t - 
 if xi = 0
if xi = 0  if xi = x0
if xi = x0


(iv) if u = - u0 , a = +a0
x = xi - u0t + 




(v) If u = u0, a = - a0
x = xi - u0t - 




Ex. 25: Draw the :
(a) position vs time graph
(b) velocity vs time graph
(c) acceleration vs time graph
for the following cases :
(i) If a body is projected vertically upwards with initial velocity u. Take the projection point to be origin and upward direction as positive.




(ii) If a body is dropped from a height h above the ground. Take dropping point to be origin and upward direction as ve.
x = 

 v = - gt
v = - gt 
(iii) If a body is projected vertically upwards from a tower of height h with initial velocity u. Take the projection point to be origin and upward direction as +ve.
 v = u - gt
v = u - gt 

(iv) A car starting from rest accelerates uniformly at 2 ms-2 for 5 seconds and then moves with constant speed acquired for the next 5 seconds and then comes to rest retarding at 2 ms-2.
Draw its :
(a) position vs time graph,
(b) Velocity vs time graph,
(c) acceleration vs time graph.
acceleration vs time graph :



acceleration vs time graph velocity vs time graph position vs time graph.
(v) A particle starts from x = 0 and initial speed 10 ms-1 and moves with constant speed 10ms-1 for 20 sec. and then retarding uniformly comes to rest in next 10 seconds.
acceleration vs time graph :


Acceleration vs time graph velocity vs time graph

position vs time graph
(V) Conversion of velocity v/s time graph to speed v/s time graph.
As we know that magnitude of velocity represent speed therefore whenever velocity goes -ve take its mirror image about time axis.
Ex. 26:


Ex. 27:

(VI) Conversion of displacement vs time graph to distance vs time graph

For distance time graph just make the mirror image of the displacement time graph from point of zero velocity onwards.
(VII) Conversion of v - t graphs in to x-t and a-t graphs
(i)  ⇒
⇒ 
(ii)  ⇒
⇒  a - t graph
a - t graph 
(iii)  ⇒
⇒ 

at t = t0 velocity reverses its direction.
(iv) x - t graph
From t = 0 to t = t1 acceleration = 0 therefore
from t = 0 to t = t1, x - t graph will be a straight line.
From t = t1 to t2 acceleration is negative
 It will be an opening downward parabola.
It will be an opening downward parabola.


(v) upto t = t1 acceleration is ve
t1 < t < t2 acceleration is zero.
t > t2 acceleration is -ve
x - t graph


Some important points :
a =  ⇒
⇒  =
= 
⇒ Δv = area under the a - t curve
v =  ⇒
⇒ 
⇒ Δx = area under the v - t curve
⇒ displacement = area under the v - t curve.
Ex. 28: If at t = 0 u = 5 ms-1 then velocity at t = 10 sec

= u + change in velocity
= 5 + area of the shaded part
= 5 + 10 × 5
= 55 ms-1
Ex. 29: If at t = 0, u = 2 ms-2 find out it maximum velocity

Since whole motion is accelerating. Therefore velocity
will be max at the end of the motion which will be
= 2  × 5 × 10 = 27 ms-1
× 5 × 10 = 27 ms-1
Ex. 30: If at t = 0, u = 4 ms-1
Find out v at
t = 10 sec, t = 20 sec & t = 30 sec.

Since for whole motion acceleration of the body is positive
vt= 10 sec = 4 × 10 × 10 = 54 ms-1
vt = 20 sec = 4 +  × 10 × 10 + 10 × 10
× 10 × 10 + 10 × 10
= 154 ms-1
vt = 30 sec = 154 × 10 × 10 = 204 ms-1
(VIII) Reading of graphs if the motion of two bodies are sketched on the same axes.
(a) Reading of x - t graphs

Conclusions :
(i) Body A Start its motion at t = 0 from origin and is moving away from the origin with constant velocity. Finally it ends its motion at a distance of x2m from origin at t = t3.
(ii) Body B starts its motion at t = t1 from origin and is moving away from origin with constant velocity. Finally it ends its motion at a distance of x3m from origin at t = t3
(iii) Since slope of B is greater than slope of A. Therefore velocity of B is greater than velocity of A.
(iv) A t = t2, Both A & B are at the same distance from starting point that means B overtakes A at t = t2
(v) Q velocity of both A & B are constant
Q acceleration of both the bodies are zero.
(vi)  x3 > x2
x3 > x2
 At the end of the motion B is at a greater distance from the starting point.
At the end of the motion B is at a greater distance from the starting point.
Ex. 31:

Conclusion :
(i) Body A starts its motion at t = 0 from origin and is moving away from the origin with constant velocity. Finally its motion ends at t = t1 at x = x2 m.
(ii) Body B starts its motion at t = 0 from x = x0 and then moves with constant velocity away from the origin. Finally it ends its motion at t = t1.
(iii) Velocity of A is greater than that of B.
(iv) At t = t0 A overtakes B
(v) acceleration of both A & B is zero.
(vi) Q x2 > x1
 At the end of the motion A is at a greater distance from the starting point then B.
At the end of the motion A is at a greater distance from the starting point then B.
Ex-32
Conclusions :
(i) Both A & B starts their motion at same time t = 0 and from same point x = 0.
(ii) Both are moving away from the starting point.
(iii) A is moving with constant velocity while B starts its motion from rest and its velocity is increasing with time i.e. it has some positive acceleration.
(iv) Q At t = t1 the tangent on B's graph becomes parallel to the A's graphs
 At t = t1 velocity of both A & B is same.
At t = t1 velocity of both A & B is same.
(v) For t < t1 velocity of A is greater than velocity of B. Therefore up to t = t1, separation between A & B increases with time.
(vi) For t > t1 velocity of B is greater than velocity of A. Therefore after t = t1 separation between A & B starts decreasing and it becomes zero at t = t2 where B overtakes A.
 Now you can try Questions 14 to 38 in Exercise I and Ques. 7 to 11 in Ex.II
Now you can try Questions 14 to 38 in Exercise I and Ques. 7 to 11 in Ex.II
4. Two dimensional motion or motion in a plane :
Motion in a plane can be described by vector sum of two independent 1D motions along two mutual perpendicular directions (as motions along two mutual directions don't affect each other).
Consider a particle moving in X-Y plane, then its equations of motions for X and Y axes are
vx = ux axt, vy = uy ayt
x = uxt  axt2, and ; y = uyt ayt2, and
axt2, and ; y = uyt ayt2, and


where symbols have their usual meanings. Thus resultant motion would be described by the equations
 and
and 
4.1 Projectile Motion :
It is the best example to understand motion in a plane. If we project a particle obliquely from the surface of earth, as shown in the figure below, then it can be considered as two perpendicular 1D motions - one along the horizontal and other along the vertical
 ⇒
⇒ 

Assume that effect of air friction and wind resistance are negligible and value of `acceleration due to gravity  is constant.
is constant.
Take point of projection as origin and horizontal and vertical direction as ve X and Y-axes, respectively.
For X-axis For Y - axis :
ux = u cosθ, uy = u sinθ
ax = 0, ay = - g,
vx = u cosθ, and vy = u sinθ - gt, and
x = u cosθ × t y = u sinθ t -  gt2
gt2
It is clear from above equations that horizontal component of velocity of the particle remains constant while vertical component of velocity is first decreasing, gets zero at the highest point of trajectory and then increases in the opposite direction. At the highest point, speed of the particle is minimum.
The time, which projectile takes to come back to same (initial) level is called the time of flight (T).
At initial and final points, y = 0,
So u sinθ t -  gt2 = 0
gt2 = 0
⇒ t = 0 and  So, T =
So, T = 
Range (R) : The horizontal distance covered by the projectile during its motion is said to be range of the projectile
R = u cosθ × T = 
For a given projection speed, the range would be maximum for q = 45°.
Maximum height attained by the projectile is
H = 
at maximum height the vertical component of velocity is 0.
Time of ascent = Time of descent =  =
= 
 Speed, kinetic energy, momentum of the particle initialy decreases in a projectile motion and attains a minimum value (not equal to zero) and then again increases.
Speed, kinetic energy, momentum of the particle initialy decreases in a projectile motion and attains a minimum value (not equal to zero) and then again increases.
 θ is the angle between
θ is the angle between  and horizontal which decreases to zero. (at top most point) and again increases in the negative direction.
and horizontal which decreases to zero. (at top most point) and again increases in the negative direction.
Ex. 33: A body is projected with a velocity of 30 ms-1 at an angle of 30° with the vertical. Find the maximum height, time of flight and the horizontal range.
Sol. Here u = 30 ms-1,
Angle of projection, q = 90 - 30 = 60°
Maximum height,
H =  =
=  = 34.44 m
= 34.44 m
Time fo flight,
T =  =
=  = 5.3 s
= 5.3 s
Horizontal range,
R =  =
=  =
=  = 79.53 m.
= 79.53 m.
Ex. 34: Find out the relation between uA, uB, uC (where uA, uB, uC are the initial velocities of particles A, B, C, respectively)

Sol.  Hmax is same for all three particle A, B, C
Hmax is same for all three particle A, B, C
⇒ Hmax = 
⇒ uy is same for all  uyA = uyB = uyC
uyA = uyB = uyC
⇒ TA = TB = TC
from figure RC > RB > RA Q R = 
⇒ uxC > uxB > uxA ⇒ uA < uB< uC
(C) Coordinate of a particle after a given time t :
Particle reach at a point p after time t then

x = ucosθ .t
y = usinθ.t - 
position vector

(D) Velocity and direction of motion after a given time :
After time 't' vx = ucosθ and vy = usinq - gt
Hence resultant velocity v =  =
= 
tan a =  =
=  ⇒ a =
⇒ a = 
(E) Velocity and direction of motion at a given height :
At a height 'h', vx = ucosq
And vy = 
 Resultant velocity
Resultant velocity
v =  =
= 
v = 
Note that this is the velocity that a particle would have at height h if it is projected vertically from ground with u.
Ex. 35: A body is projected with a velocity of 20 ms-1 in a direction making an angle of 60° with the horizontal. Calculate its (i) position after 0.5 s and (ii) velocity after 0.5 s.
Sol. Here u = 20 ms-1, θ = 60° , t = 0.5 s
(i) x = (u cosθ)t = (20 cos60°) × 0.5 = 5 m
y = (u sin θ) t -  = (20 × sin 60°) × 0.5
= (20 × sin 60°) × 0.5
-  × 9.8 × (0.5)2 = 7.43 m
× 9.8 × (0.5)2 = 7.43 m
(ii) vx = u cos θ = 20 cos 60° = 10 ms-1
vy = u sin θ - gt = 20 sin 60° - 9.8 × 0.5
= 12.42 ms-1
 v =
v =  =
=  =15.95 ms-1 tan b =
=15.95 ms-1 tan b =  =
=  = 1.242
= 1.242
 b = tan-1 1.242 = 51.16°.
b = tan-1 1.242 = 51.16°.
Equation of trajectory of a projectile :
Suppose the body reaches the point p(x, y) after time t.

Q The horizontal distance covered by the body in time t,
x = Horizontal velocity × time = u cos θ. t
or t = 
For vertical motion : u = u sinθ, a = -g, so the vertical distance covered in time t is given by
s = ut +  or y = u sin θ.
or y = u sin θ. -
- 
or y = x tanq -  ...(1)
...(1)
or y = px - qx2, where p and q are constants.
Thus y is a quadratic function of x. Hence the trajectory of a projectile is a parabola.
From equation (1)
y = x tan θ  ⇒ y = x tan θ
⇒ y = x tan θ 
y = x tan θ ...(2)
...(2)
Equation (2) is another form of trajectory equation of projectile.
Ex. 36: A ball is thrown from ground level so as to just clear a wall 4 m high at a distance of 4 m and falls at a distance of 14 m from the wall. Find the magnitude and direction of the velocity.
Sol. The ball passes through the point p(4, 4). So its range = 4 + 14 = 18m.
The trajectory of the ball is,
Now x = 4m, y = 4m and R = 18 m
 4 = 4 tan θ
4 = 4 tan θ  = 4 tanθ .
= 4 tanθ .
or tan θ =  , sin θ =
, sin θ =  , cosθ=
, cosθ= 
or u2 =  = 182
= 182
or u =  = 13.5 ms-1
= 13.5 ms-1
Also q = tan-1(9/7) = 52.1°
Ex. 37: A particle is projected over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If a and b be the base angles and q the angle of projection, prove that tan θ = tan α + tan β.
Sol. If R is the range of the particle, then from the figure we have
tan α + tan β =  +
+ =
= 
or tan α +tan β =  ...(1)
...(1)
Also, the trajectrory of the particle is
y = x tan θ 
or tanθ = 
From equations (1) and (2), we get
tan q = tan α + tan β.
4.2 projectile fired parallel to horizontal :
As shown in shown figure suppose a body is projected horizontally with velocity u from a point O at a certain height h above the ground level. The body is under the influence of two simultaneous independent motions:

(i) Uniform horizontal velocity u.
(ii) Vertically downward accelerated motion with constant acceleration g.
Under the combined effect of the above two motions, the body moves along the path OpA.
Trajectory of the projectile : After the time t, suppose the body reaches the point p(x, y).
The horizontal distance covered by the body in time t is
x = ut  t =
t = 
The vertical distance travelled by the body in time t is given by
s = ut + 
or y = 0 × 1 + =
= 
[For vertical motion, u = 0]
or 

or y = kx2 [Here k =  = a constant]
= a constant]
As y is a quadratic function of x, so the trajectory of the projectile is a parabola.
Time of Flight : It is the total time for which the projectile remains in its flight (from 0 to A). Let T be its time of flight.
For the vertical downward motion of the body,
we use
s = ut +
or h = 0 × T +  or T =
or T = 
Horizontal Range: It is the horizontal distance covered by the projectile during its time of flight. It is equal to OA = R. Thus R = Horizontal velocity × time of flight = u × T
or R = u
Velocity of the Projectile at any Instant : At the instant t (when the body is at point p), let the velocity of the projectile be v. The velocity v has two rectangular components:
Horizontal component of velocity, vx = u
Vertical component of velocity, vy = 0 + gt = gt
 The resultant velocity at point p is
The resultant velocity at point p is
 =
= 
If the velocity v makes an angle b with the horizontal, then
tan β =  =
=  or β = tan-1
or β = tan-1
Ex. 38: A body is thrown horizontally from the top of a tower and strikes the ground after three seconds at an angle of 45° with the horizontal. Find the height of the tower and the speed with which the body was projected. Take g = 9.8 ms-2.
Sol. As shown in figure, suppose the body is thrown horizontally from the top O of a tower of height y with velocity u. The body hits the ground after 3s. Considering verticlly downward motion of the body,
y = uyt + = 0 × 3 +
= 0 × 3 +  ×9.8 × (3)2 = 44.1 m [
×9.8 × (3)2 = 44.1 m [ Initial vertical velocity, uy = 0]
Initial vertical velocity, uy = 0]
Final vertical velocity,
vy = uy + gt = 0 9.8 × 3 = 29.4 ms-1
Final horizontal velocity, vx = u
As the resultant velocity u makes an angle of 45° with the horizontal, so
tan 45° =  or 1 =
or 1 =  or u = 29.4 ms-1
or u = 29.4 ms-1
Ex. 39: A particle is projected horizontally with a speed u from the top of plane inclined at an angle q with the horizontal. How far from the point of projection will the particle strike the plane?
Sol.

The horizontal distance covered in time t,
x = ut or t = 
The vertical distance covered in time t,
y = 0 +  =
=  [using (1)]
[using (1)]
Also  or y = x tan θ
or y = x tan θ 

or 
As x = 0 is not possible, so x = 
The distance of the point of strike from the point of projection is
D =  =
= 
= x  = x sec θ or D =
= x sec θ or D = 
Ex. 40: A ball rolls off the top of a stairway with a constant horizontal velocity u. If the steps are h metre high and w meter wide, show that the ball will just hit the edge of nth step if n = 
Sol. Refer to figure.

For n th step,
net vertical displacement = nh
net horizontal displacement = nω
Let t be the time taken by the ball to reach the nth step. Then
R = ut
or nω = ut or t = 
Also, y = uy t 
or nh = 0  =
=  or n =
or n = 
4.3 Projectile at an Angle q from Height h :
Consider the projectile as shown in the adjacent figure.

Take the point of projection as the origin the X and Y-axes as shown in figure.
For X-axis,
ux = u cosθ
ax = 0
vx = u cosθ, and
x = u cos θ × t
For Y-axis,
uy = u sin θ,
ay = -g,
vy = u sin θ - gt, and y = u sin θ t - 
Ex. 41: From the top of a tower 156.8 m high a projectile is projected with a velocity of 39.2 ms-1 in a direction making an angle 30° with horizontal. Find the distance from the foot of tower where it strikes the ground and time taken to do so.
Sol. The situation is shown

Here height of tower
OA = 156.8 m
u = 39.2 ms-1
θ = 30°
time for which projectile remain is air = t = ?
Horizontal distance covered R = OD = ?
Now ux = u cos θ and
uy = u sin θ be the components of velocity .
Motion of projectile from O to H to D
Using equation y = uyt + 
Here : y = 156.8 m ; uy = - u sinθ
= 39.2 sin 30°
ay = 9.8 m/s2 ; t = ?
156.8 = - 39.2 × 0.5 t + 4.9 t2
156.8 = - 19.6 t + 4.9 t2
or 4.9 t2 - 19.6 t - 156.8 = 0
or t2 - 4t - 32 = 0 ⇒ (t - 8) (t + 4) = 0
We get t = 8 s; t = - 4s
t = - 4 s is not possible, thus we take t = 8s.
Now horizontal distance covered in this time
R = ux × t = u cos θ × t = 39.2 × cos 30° × t
R = 271.57 m.
4.4 Projectile Motion in Inclined Plane :
Here, two cases arise. One is up the plane and the other is down the plane. Let us discuss both the cases separately.
(i) Up the Plane : In this case direction x is chosen up the plane and direction y is chosen perpendicular to the plane. Hence,
ux = u cos α , ax = - g sin β
uy = u sin α and ay = - g cos β



Now, let us derive the expressions for time of flight (T) and range (R) along the plane.
Time of Flight :
At point B displacement along y-direction is zero. So, substituting the proper values in sy = uyt  , we get
, we get
0 = ut sin a  (- g cos β) t2
(- g cos β) t2 t = 0 and
t = 0 and 
t = 0, corresponds to point O and t =  corresponds to point B. Thus,
corresponds to point B. Thus,
T = 
Range :
Range (R) or the distance OB is also equal to be displacement of projectile along x-direction in the
t = T. Therefore.
R = sa = uxT  ⇒ R = u cos a T -
⇒ R = u cos a T -  sin b T2
sin b T2
(ii) Down the inclined Plane :
along x - axis y-axis
(1) ux = ucos α (1) uy = usinα
(2) ax = g sin β (2) ay = g cos β
velocity at p
vy = uy + ay T
vx = ux + axT
Time of flight T =  =
= 

Range Sx = ux T +
= u cos a T +
Ex. 42: A particle is projected at an angle a with horizontal from the foot of a plane whose inclination to horizontal is β. Show that it will strike the plane at right angles if cotβ = 2 tan (α - β)
Sol. Let u be the velocity of projection so that u cos (α - β) and u sin (α - β) are the initial velocities respectively parallel and perpendicular to the inclined plane. The acceleration in these two directions are (-g sin β) and (-g cosβ).
The initial component of velocity perpendicular to pQ is u sin (α - β) and the acceleration in this direction is (-g cosβ). If T is the time the particle takes to go from p to Q then in time T the space described in a direction perpendicular to pQ is zero.
0 = u sin (α - β).T - g cos β.T2
T = 

If the direction of motion at the instant when the particle hits the plane be perpendicular to the plane, then the velocity at that instant parallel to the plane must be zero.
 u cos (α - β) - g sin βT = 0
u cos (α - β) - g sin βT = 0
 = T =
= T = 
 cosb = 2 tan (α - β)
cosb = 2 tan (α - β)
Ex. 43: Two inclined planes OA and OB having inclinations 30° and 60° with the horizontal respectively intersect each other at O, as shwon in figure. a particle is projected from point p with velocity u =  along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular of flight, then calculate.
along a direction perpendicular to plane OA. If the particle strikes plane OB perpendicular of flight, then calculate.

(a) time of flight
(b) velocity with which the particle strikes the plane OB,
(c) height h of point p from point O
(d) distance pQ. (Take g = 10 m/s2)
Sol. Let us choose the x and y directions along OB and OA respectively. Then,
ux = u = m/s, uy = 0
ax = - g sin 60° = - 5 m/s2
m/s2
and ay = - g cos 60° = - 5 m/s2
(a) At point Q, x-component of velocity is zero. Hence, substituting in
vx= ux + axt
0 = ⇒ t =
⇒ t =  = 2s Ans.
= 2s Ans.
(b) At point Q, v = vy = uy + ayt
 v = 0 - (5) (2) = -10 m/s Ans.
v = 0 - (5) (2) = -10 m/s Ans.
Here, negative sign implies that velocity of particle at Q is along negative y direction.
(c) Distance PO = |displacement of particle along y-direction| = |sy|
Here, sy = uyt +  = 0 -
= 0 -  = - 10 m
= - 10 m
 PO = 10 m
PO = 10 m
Therefore, h = PO sin 30° = (10)  or h = 5m Ans.
or h = 5m Ans.
(d) Distance OQ = displacement of particle along x-direction = sx
Here, sx = uxt +  =
=  -
-  =
= 
or OQ = 
PQ =  =
=  =
= 
PQ = 20 m Ans.
 Now you can try Questions 45 to 68 in Exercise I and Ques. 12 to 20 in Ex.II
Now you can try Questions 45 to 68 in Exercise I and Ques. 12 to 20 in Ex.II
5. Relative Motion :
The word 'relative' is a very general term, which can be applied to physical, nonphysical, scalar or vector quantities. For example, my height is five feet and six inches while my wife's height is five feet and four inches. If I ask you how high I am relative to my wife, your answer will be two inches. What you did? You simply subtracted my wife's height from my height. The same concept is applied everywhere, whether it is a relative velocity, relative acceleration or anything else. So, from the above discussion we may now conclude that relative velocity of A with respect of B (written as  ) is
) is

Similarly, relative acceleration of A with respect of B is

If it is a one dimensional motion we can treat the vectors as scalars just by assigning the positive sign to one direction and negative to the other. So, in case of a one dimensional motion the above equations can be written as
vAB = vA - vB
and aAB = aA - aB
Further, we can see that
 or
or 
Ex. 44: Seeta is moving due east with a velocity of 1 m/s and Geeta is moving the due west with a velocity of 2 m/s. What is the velocity of Seeta with respect to Geeta?
Sol. It is a one dimensional motion. So, let us choose the east direction as positive and the west as negative. Now, given that
vs = velocity of Seeta = 1 m/s
and vG = velocity of Geeta = - 2m/s
Thus, vSG = velocity of Seeta with respect to Geeta
= vS - vG = 1 - (-2) = 3 m/s
Hence, velocity of Seeta with respect to Geeta is 3 m/s due east.
Important Note :
Procedure to solve the vector equation :
 ...(1)
...(1)
(a) Their are 6 variables in this equation which are following :
(1) Magnitude of  and its direction
and its direction
(2) Magnitude of  and its direction
and its direction
(3) Magnitude of  and its direction.
and its direction.
(b) We can solve this equation if we know the value of 4 variables [Note : two of them must be directions].
(c) If we know the two direction of any two vectors then we will put them on the same side and other on the different side.
For example :
If we know the directions of  and
and  and
and  direction is unknown then we make equation as follows : -
direction is unknown then we make equation as follows : -

(d) Then we make vector diagram according to the equation and resolve the vectors to know the unknown values.
Ex. 45: Car A has an acceleration of 2 m/s2 due east and car B, 4 m/s2 due north. What is the acceleration of car B with respect to car A?
Sol. It is a two dimensional motion. Therefore,

 = acceleration of car B with respect to car A
= acceleration of car B with respect to car A
= 
Here,  = acceleration of car
= acceleration of car
B = 4 m/s2 (due north)
and  = acceleration of car A = 2 m/s2 (due east)
= acceleration of car A = 2 m/s2 (due east)


and  = tan-1(2)
= tan-1(2)
Thus,  is
is  m/s2 at an angle of α = tan-1(2)
m/s2 at an angle of α = tan-1(2)
from west towards north.
Ex. 46: Three particle A, B and C situated at the vertices of an equilateral triangle starts moving simultaneously at a constant speed "v" in the direction of adjacent particle, which falls ahead in the anti-clockwise direction. If "a" be the side of the triangle, then find the time when they meet.
Sol. Here, particle "A" follows "B", "B" follows "C" and "C" follows "A". The direction of motion of each particle keeps changing as motion of each particle is always directed towards other particle. The situation after a time "t" is shown in the figure with a possible outline of path followed by the particles before they meet.

This problem appears to be complex as the path of motion is difficult to be defined. But, it has a simple solution in component analysis. Let us consider the pair "A" and "B". The initial component of velocities in the direction of line joining the initial position of the two particles is "v" and "vcosθ" as shown in the figure here :

The component velocities are directed towards eachother. Now, considering the linear (one dimensional) motion in the direction of AB, the relative velocity of "A" with respect to "B" is :
vAB = vA - vB
vAB = v - (- v cos θ) = v vcosθ
In equilateral triangle, q = 60°
vAB = v vcos60° = v +  =
= 
The time taken to cover the displacement "a" i.e. the side of the triangle
t = 
Questions based on relative motion are usually of following four types :
(a) Minimum distance between two bodies in motion
(b) River-boat problems
(c) Aircraft-wind problems
(d) Rain problems
(a) Minimum distance between two bodies in motion :
When two bodies are in motion, the questions like, the minimum distance between them or the time when one body overtakes the other can be solved easily by the principle of relative motion. In these type of problems one body is assumed to be at rest and the relative motion of the other body is considered. By assuming so two body problem is converted into one body problem and the solution becomes easy. Following example will illustrate the statement.
Ex. 47: Car A and car B start moving simultaneously in the same direction along the line joining them. Car A with a constant acceleration a = 4 m/s2, while car B moves with a constant velocity v = 1 m/s. At time t = 0, car A is 10 m behind car B. Find the time when car A overtakes car B.
Sol. Given : uA = 0, uB = 1 m/s, aA = 4m/s2 and aB = 0
Assuming car B to be at rest, we have
uAB = uA - uB = 0 - 1 = - 1 m/s
aAB = aA - aB = 4 - 0 = 4 m/s2
Now, the problem can be assumed in simplified form as follow :

Substituting the proper values in equation

s = ut + 
we get 10 = - t + or 2t2 - t - 10 = 0
or 2t2 - t - 10 = 0
or 
 or t = 2.5 s and - 2 s
or t = 2.5 s and - 2 s
Ignoring the negative value, the desired
time is 2.5s. Ans.
Note : The above problem can also be solved without using the concept of relative motion as under.
At the time when A overtakes B,
sA = sB + 10


or 2t2 - t - 10 = 0
Which on solving gives t = 2.5 s and - 2 s, the same as we found above.
As per my opinion, this approach (by taking absolute values) is more suitable in case of two body problem in one dimensional motion. Let us see one more example in support of it.
Ex. 48: An open lift is moving upwards with velocity 10m/s. It has an upward acceleration of 2m/s2. A ball is projected upwards with velocity 20 m/s relative to ground. Find :
(a) time when ball again meets the lift.
(b) displacement of lift and ball at that instant.
(c) distance travelled by the ball upto that instant. Take g = 10 m/s2
Sol. (a) At the time when ball again meets the lift :
sL = sB
 10t +
10t +  × 2 × t2 = 20 t -
× 2 × t2 = 20 t -  × 10t2
× 10t2

Solving this equation, we get
t = 0 and 
 Ball will again meet the lift after
Ball will again meet the lift after  .
.
(b) At this instant :

(c) For the ball  . Therefore, we will first find t0, the time when its velocity becomes zero :
. Therefore, we will first find t0, the time when its velocity becomes zero :

As  distance and displacement are equal
distance and displacement are equal
or d = 19.4 m Ans.
Concept of relative motion is more useful in two body problem in two (or three) dimensional motion. This can be understood by the following example.
Ex. 49: Two ships A and B are 10 km apart on a line running south to north. Ship A farther north is streaming west at 20 km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it ?
Sol. Ships A and B are moving with same speed 20 km/h in the directions shown in figure. It is a two dimensional, two body problem with zero acceleration. Let us find 


Here, 

i.e.,  is
is  at an angle of 45º from east towards north. Thus, the given problem can be simplified as :
at an angle of 45º from east towards north. Thus, the given problem can be simplified as :
A is at rest and B is moving with  in the direction shown in figure.
in the direction shown in figure.

Therefore, the minimum distance between the two is
smin = AC = AB sin 45º
 =
=  Ans.
Ans.
and the desired time is
 (BC = AC =
(BC = AC =  )
)
 Ans.
Ans.
(B) river - Boat problems
In river-boat problems we come across the following three terms :



 = absolute velocity of river
= absolute velocity of river
 = velocity of boatman with respect to river or velocity of boatman is still water
= velocity of boatman with respect to river or velocity of boatman is still water
and  = absolute velocity of boatman.
= absolute velocity of boatman.
Here, it is important to note that  is the velocity of boatman with which he steers and
is the velocity of boatman with which he steers and  is the actual velocity of boatman relative to ground.
is the actual velocity of boatman relative to ground.
Further,  =
= 
Now, let us derive some standard results and their special cases.
A boatman starts from point A on one bank of a river with velocity  in the direction shown in fig. River is flowing along positive x-direction with velocity . Width of the river is w, then
in the direction shown in fig. River is flowing along positive x-direction with velocity . Width of the river is w, then
 =
= 
Therefore, vbx = vrx + vbrx = vr - vbr sinθ
and vby = vry + vbry
= 0 + vbr cosθ = vbr cosθ
Now, time taken by the boatman to cross the river is :
t = 
or t =  ...(i)
...(i)
Further, displacement along x-axis when he reaches on the other bank (also called drift) is :
x = vbx t = (vr - vbr sin q) 
or x = (vr - vbr sinq) ...(ii)
...(ii)
Three special are :
(i) Condition when the boatman crosses the river in shortest interval of time :
From Eq.(i) we can see that time (t) will be minimum when q = 0°, i.e., the boatman should steer his boat perpendicular to the river current.

Also, tmin =  as cos θ = 1
as cos θ = 1
(ii) Condition when the boatman wants to reach point B, i.e., at a point just opposite from where he started :
In this case, the drift (x) should be zero.
 x = 0
x = 0

or (vr - vbr sinq) 
or vr = vbr sin θ
or sinθ =  or θ =
or θ = 
Hence, to reach point B the boatman should row at an angle θ=  upstream from AB.
upstream from AB.
Further, since sinq not greater than 1.
So, if vr > vbr, the boatman can never reach at point B. Because if vr = vbr, sin θ = 1 or q = 90° and it is just impossible to reach at B if = 90°. Moreover it can be seen that vb = 0 if vr = vbr and θ = 90°. Similarly, if vr > vbr, sinq > 1, i.e., no such angle exists. practically it can be realized in this manner that it is not possible to reach at B if river velocity (vr) is too high.
(iii) Shortest path :
path length travelled by the boatman when he reaches the opposite shore is
s = 
Here, w = width of river is constant. So for s to be minimum modulus of x (drift) should be minimum. Now two cases are possible.
When vr < vbr : In this case x = 0,
when θ =  or smin = w at θ =
or smin = w at θ = 
When vr > vbr : In this case x is minimum, where 
or 
or -vbr cos2θ - (vr - vbr sinq) (- sinθ) = 0
or - vbr vr sinθ = 0
or θ = sin-1
Now, at this angle we can find xmin and then smin which comes out to be
smin =  at θ =
at θ = 
Ex. 50: A man can row a boat with 4 km/h in still water. If he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be headed, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river is 4 km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction should he head the boat if he wants to cross the river in shortest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point ?
Sol. (a) Given, that vbr = 4 km/h and vr = 2 km/h
 θ = sin-1
θ = sin-1 = sin-1
= sin-1 = sin-1
= sin-1 = 30°
= 30°
Hence, to reach the point directly opposite to starting point he should head the boat at an angle of 30° with AB or 90° + 30° = 120° with the river flow.
(b) Time taken by the boatman to cross the river
w = width of river = 4 km
vbr = 4 km/h and θ = 30°
 t =
t =  =
=  Ans.
Ans.
(c) For shortest time θ = 0°
and tmin =  =
=  = 1h
= 1h
Hence, he should head his boat perpendicular to the river current for crossing the river in shortest time and this shortest time is 1 h.

(d) t = tCD + tDC
or  =
=  Ans.
Ans.
Ex. 51: A man can swim at a speed of 3 km/h in still water. He wants to cross a 500 m wide river flowing at 2 kh/h. He keeps himself always at an angle of 120° with the river flow while swimming.
(a) Find the time he takes to cross the river.
(b) At what point on the opposite bank will he arrive ?
Sol. The situation is shown in figure

Here  = velocity of the river with respect to the ground
= velocity of the river with respect to the ground
 = velocity of the man with respect to the river
= velocity of the man with respect to the river
 = velocity of the man with respect to the ground.
= velocity of the man with respect to the ground.
(a) We have
 ...(i)
...(i)
Hence, the velocity with respect to the ground is along AC.
Taking y-components in equation (i),
 = 3 km/h cos 30° + 2 km/h cos 90° =
= 3 km/h cos 30° + 2 km/h cos 90° =  km/h
km/h
Time taken to cross the river
=  =
= 
(b) Taking x-components in equation (i),
 = -3km/h sin 30° + 2 km/h
= -3km/h sin 30° + 2 km/h 
Displacement along the X-axis as the man crosses the river
= (velocity along the X-axis) (time)
=  ×
×  =
= 
Ex. 52: A boat moves relative to water with a velocity v and river is flowing with 2v. At what angle the boat shall move with the stream to have minimum drift?
(A) 30°
(B) 60°
(C) 90°
(D) 120°
Sol.
(D) Let boat move at angle θ to the normal as shown in figure then time to cross the river = 
drift x = (2v - v sin θ) for x to be minimum
for x to be minimum
 = 0 = 1 (2 sec θ tan θ - sec2θ) or sin θ = 1/2
= 0 = 1 (2 sec θ tan θ - sec2θ) or sin θ = 1/2
or θ = 30° and φ= 90 30 = 120°
(C) Aircraft Wind problems :
This is similar to river boat problem. The only difference is that  is replaced by
is replaced by  (velocity of aircraft with respect to wind or velocity of aircraft in still air),
(velocity of aircraft with respect to wind or velocity of aircraft in still air),  is replaced by
is replaced by  (velocity of wind) and
(velocity of wind) and  is replaced by
is replaced by  (absolute velocity of aircraft). Further,
(absolute velocity of aircraft). Further,  =
=  . The following example will illustrate the theory.
. The following example will illustrate the theory.
Note : Short - Trick
If their are two vectors  and
and  and their resultent make an anlge a with and b with
and their resultent make an anlge a with and b with  .
.

then A sinα = b sin β
Means component of  perpendicular to resultant is equal in
perpendicular to resultant is equal in
magnitude to the compopent of  also perpendicular to resultant.
also perpendicular to resultant.
Ex. 53: If two vectors and make angle 30° and 60° with their resultent and  has magnitude equal to 10, then find magnitude of
has magnitude equal to 10, then find magnitude of  .
.

So B sin 60° = A sin 30°
⇒ 10 sin 60° = A sin 30°
⇒ A = 
Ex. 54: An aircraft flies at 400 km/h in still air. A wind of  km/h is blowing from the south. The pilot wishes to travel from A to a point B north east of A. Find the direction he must steer and time of his journey if AB = 1000 km.
km/h is blowing from the south. The pilot wishes to travel from A to a point B north east of A. Find the direction he must steer and time of his journey if AB = 1000 km.
Sol. Given that vw = 200 km/h
km/h
vaw = 400 km/h and  should be along AB or in north-east direction. Thus, the direction of
should be along AB or in north-east direction. Thus, the direction of  should be such as the resultant of
should be such as the resultant of  and
and  is along AB or in north - east direction.
is along AB or in north - east direction.
Let  makes an angle a with AB as shown in figure.
makes an angle a with AB as shown in figure.

Applying sine law in triangle ABC, we get

or sin α =  sin 45° =
sin 45° = 

 α = 30°
α = 30°
Therefore, the pilot should steer in a direction at an angle of (45° +α) or 75° from north towards east.
Further,  =
=  or
or  =
=  × (400)
× (400) 
=  (400)
(400)  =
=  (400)
(400) 
= 546.47 km/h
 The time of journey from A to B is
The time of journey from A to B is
t =  ⇒ t = 1.83 h
⇒ t = 1.83 h
(D) Rain problems :
In these type of problems we again come across three terms  ,
,  and
and  , Here,
, Here,
 = velocity of rain
= velocity of rain
 = velocity of man (it may be velocity of cyclist or velocity of motorist also)
= velocity of man (it may be velocity of cyclist or velocity of motorist also)
and  = velocity of rain with respect to man.
= velocity of rain with respect to man.
Here,  is the velocity of rain which appears to the man. Now, let us take one example of this.
is the velocity of rain which appears to the man. Now, let us take one example of this.
Ex. 55: A man standing on a road has to hold his umbrella at 30° with the vertical to keep the rain away. He throws the umbrella and starts running at 10 km/h. He finds that raindrops are hitting his head vertically. Find the speed of raindrops with respect to
(a) the road,
(b) the moving man.
Sol. When the man is at rest with respect to the ground, the rain comes to him at an angle 30° with the vertical. This is the direction of the velocity of raindrops with respect to the ground. The situation when the man runs is shown in the figure



Here  = velocity of the rain with respect to the ground
= velocity of the rain with respect to the ground
 = velocity of the man with respect to the ground and
= velocity of the man with respect to the ground and  = velocity of the rain with respect to the man.
= velocity of the rain with respect to the man.
We have,  ...(i)
...(i)
Taking horizontal components, equation (i) gives
vr,g sin30° = um,g = 10 km/h or, v,g = 
Taking vertical components, equation (i) gives
vr,g cos30° = vr,m or, vr,m = (20 km/h)  = 10 Ö 3 km/h.
= 10 Ö 3 km/h.
Ex. 56: To a man walking at the rate of 3 km/h the rain appears to fall vertically. When the increases his speed to 6 km/h it appears to meet him at an angle of 45° with vertical. Find the speed of rain.
Sol. Let  and
and  be the unit vectors in horizontal and vertical directions respectively.
be the unit vectors in horizontal and vertical directions respectively.
Let velocity of rain
 ...(i)
...(i)
Then speed of rain will be

In the first case  = velocity of man =
= velocity of man = 


It seems to be in vertical direction. Hence,
a - 3 = 0 or a = 3
In the second case  = 6
= 6

 = - 3
= - 3 + b
+ b
This seems to be at 45° with vertical.
Hence, |b| = 3
Therefore, from Eq. (ii) speed of rain is
 =
=  Ans.
Ans.
Relative Motion between Two Projectiles :
Let us now discuss the relative motion between two projectiles or the path observed by one projectile of the other. Suppose that two particles are projected from the ground with speeds u1 and u2 at angles α1 and α2 as shown in Fig.A and B. Acceleration of both the particles is g downwards. So, relative acceleration between them is zero because
a12 = a1 - a2 = g - g = 0


i.e., the relative motion between the two particles is uniform. Now

u1x = u1 cos α1, u2x = u2 cos α2
u1y = u1 sin α1 and u2y = u2 sin α2
Therefore, u12x = u1x - u2x = u1 cos α1- u2cos α2
and u12y = u1y - u2y = u1 sin α1- u2 sin α2
u12x and u12y are the x and y components of relative velocity of 1 with respect to 2.
Hence, relative motion of 1 with respect to 2 is a straight line at an angle  with positive x-axis.
with positive x-axis.
Now, if u12x = 0 or u1 cos α1 = u2 cos α2, the relative motion is along y-axis or in vertical direction
(as θ = 90º). Similarly, if u12y = 0 or u1 sin α1 = u2 sin α2, the relative motion is along x-axis or in horizontal direction (as θ= 0º).
Note : Relative acceleration between two projectiles is zero. Relative motion between them is uniform. Therefore, condition of collision of two particles in air is that relative velocity of one with respect to the other should be along line joining them, i.e., if two projecticles A and B collide in mid air, then  should be along AB or
should be along AB or  along BA.
along BA.
Condition for collision of two Projectiles : Consider the situation shown in the figure.

For projectiles to collide, direction of velocity of A with respect to B has to be along line AB
Here, vABx = u1 cos α1 + u2 cos α2
vABy = u1 sin α1 - u2 sin α2
Let, direction of velocity vector of A(wrt B) is making an angle b with +ve X-axis, which is given by


For collision to take place,
tan b = tan θ 
Ex. 57: A particle A is projected with an initial velocity of 60 m/s. at an angle 30º to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of p from A, where collision occurs. (g = 10 m/s2)

Sol. (a) Taking x and y directions as
shown in figure.
Here,  ,
, 
uAx = 60 cos 30º = 
uAy = 60 sin 30º = 30 m/s
uBx = - 50 cos α
and uBy = 50 sin α
Relative acceleration between the two is zero as  . Hence, the relative motion between the two is uniform. It can be assumed that B is at rest and A is moving with
. Hence, the relative motion between the two is uniform. It can be assumed that B is at rest and A is moving with  . Hence, the two particles will collide, if
. Hence, the two particles will collide, if  is along AB. This is possible only when
is along AB. This is possible only when
uAy = uBy
i.e., component of relative velocity along y-axis should be zero.
or 30 = 50 sin a
 a = sin-1 (3/5) Ans.
a = sin-1 (3/5) Ans.
(b) Now,  = (30
= (30 + 50 cosα)m/s =
+ 50 cosα)m/s =  = (30
= (30 + 40) m/s
+ 40) m/s
Therefore, time of collision is
t =  =
=  or t = 1.09 s Ans.
or t = 1.09 s Ans.
(c) Distance of point p from A where collision takes place is
s =  =
=  or s = 62.64 m Ans.
or s = 62.64 m Ans.
Ex. 58: Two projectile are projected simultaneously from a point on the ground "O" and an elevated position "A" respectively as shonw in the figure. If collision occurs at the point of return of two projectiles on the horizontal surface, then find the height of "A" above the ground and the angle at which the projectile "O" at the ground should be projected.

Sol. There is no initial separation between two projectile is x-direction. For collision to occur, the relative motion in x-direction should be zero. In other words, the component velocities in x-direction should be equal to that two projetiles cover equal horizontal distance at any given time. Hence,
uOx = uAx
⇒ u0cosθ = uA ⇒ cosθ =  =
=  =
=  = cos60° ⇒ θ = 60°
= cos60° ⇒ θ = 60°
We should ensure that collision does occur at the point of return. It means that by the time projectiles travel horizontal distances required, they should also cover vertical distances so that both projectile are at "C" at the same time. In the nutshell, their times of flight should be equal.
For projectile from "O".
T = 
For projectile from "A",

For projectile from "A",
T = 
Squaring both sides and putting values,
⇒ H =  ⇒
⇒ 

We have deliberately worked out this problem taking advantage of the fact that projectiles are colliding at the end of their flights and hence their times of flight should be equal. We can, however, proceed to analyze in typical manner, using concept of relative velocity. The initial separation between two projectiles in the vertical direction is "H". This separation is covered with the component of relative in vertical direction.
⇒ vOAy = uOy - uAy = u0 sin60° - 0 =  =
= 
Now, time of flight of projectile from ground is :
T =  =
=  =
= 
Hence, the vertical displacement of projectile from "A" before collision is :
⇒ H = vOAy x T =  = 15 m/s
= 15 m/s
Ex. 59: Two projectiles are projected simultaneously from two towers as shown in figure. If the projectiles collide in the air, then find the distance "s" between the towers.

Sol. We see here that projectiles are approaching both horizontally and vertically. Their movement in two component directions should be synchronized so that they are at the same position at a particular given time. For collision, the necessary requirement is that relative velocity and displacement should be in the same direction.

It is given that collision does occur. It means that two projectiles should cover the displacement with relative velocity in each of the component directions. In x-direction,
vABx = uAx - uBx =  - (-10) =
- (-10) =  = 20 m/s
= 20 m/s
If "t" is time after which collision occurs, then
⇒ s = vAy - uBy
⇒ vABy = u cos45° - 0 =
The initial vertical distance between points of projection is 30 - 10 = 20 m. This vertical distance is covered with component of relative velocity in vertical direction. Hence, time taken to collide, "t", is :
⇒ t = 
putting this value in the earlier equation for "s", we have :
⇒ s = 20t = 20 x 2 = 40 m
 Now you can try all the questions related to relative motion.
Now you can try all the questions related to relative motion.
FAQs on Kinematics, Chapter Notes, Class 11, Physics (IIT-JEE & AIPMT)
| 1. What is kinematics in physics? |  |
| 2. What are the three types of kinematics equations? |  |
| 3. What is the difference between distance and displacement? |  |
| 4. How can we calculate the velocity of an object? |  |
| 5. What is projectile motion? |  |

|
Explore Courses for JEE exam
|

|


















