Rotational Motion, Chapter Notes, Class 11, Physics (IIT-JEE and AIPMT) PDF Download
Rotational Motion and Moment of Inertia - System of Particles and Rotational Motion, Class 11, Physics
Rotational Motion
1. Rigid Body
Rigid body is defined as a system of particles in which distance between each pair of particles remains constant (with respect to time) that means the shape and size do not change, during the motion. Eg. Fan, Pen, Table, stone and so on.
Our body is not a rigid body, two blocks with a spring attached between them is also not a rigid body. For every pair of particles in a rigid body, there is no velocity of seperation or approach between the particles. In the figure shown velocities of A and B with respect to ground are  and
and  respectively
respectively

Note : With respect to any particle of rigid body the motion of any other particle of that rigid body is circular.
VBA = relative velocity of B with respect to A.
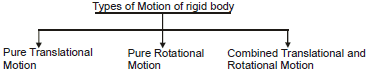
1.1. Pure Translational Motion :
A body is said to be in pure translational motion if the displacement of each particle is same during any time interval however small or large. In this motion all the particles have same  at an instant.
at an instant.
example.
A box is being pushed on a horizontal surface.

 of any particle,
of any particle,  of any particle
of any particle
 of any particle
of any particle
For pure translational motion :-


Where m1, m2, m3, ......... are the masses of different particles of the body having accelerations  respectively.
respectively.
But acceleration of all the particles are same So, 

Where M = Total mass of the body
 = acceleration of any particle or of centre of mass of body
= acceleration of any particle or of centre of mass of body

Where m1, m2, m3 ...... are the masses of different particles of the body having velocities  respectively
respectively
But velocities of all the particles are same so 

Where  = velocity of any particle or of centre of mass of the body.
= velocity of any particle or of centre of mass of the body.
Total Kinetic Energy of body = 
1.2. Pure Rotational Motion :
A body is said to be in pure rotational motion if the perpendicular distance of each particle remains constant from a fixed line or point and do not move parallel to the line, and that line is known as axis of rotation. In this motion all the particles have same  and at an instant. Eg. : - a rotating ceiling fan, arms of a clock.
and at an instant. Eg. : - a rotating ceiling fan, arms of a clock.
For pure rotation motion :-

Special case :
If α = constant,

1.3 Combined translation and rotational Motion
A body is said to be in translation and rotational motion if all the particles rotates about an axis of rotation and the axis of rotation moves with respect to the ground.
2. Moment of Inertia
Like the centre of mass, the moment of inertia is a property of an object that is related to its mass distribution. The moment of inertia (denoted by I) is an important quantity in the study of system of particles that are rotating. The role of the moment of inertia in the study of rotational motion is analogous to that of mass in the study of linear motion. Moment of inertia gives a measurement of the resistance of a body to a change in its rotaional motion. If a body is at rest, the larger the moment of inertia of a body the more difficuilt it is to put that body into rotational motion. Similarly, the larger the moment of inertia of a body, the more difficult to stop its rotational motion. The moment of inertia is calculated about some axis (usually the rotational axis).
Moment of inertia depends on :
(i) density of the material of body
(ii) shape & size of body
(iii) axis of rotation
In totality we can say that it depends upon distribution of mass relative to axis of rotation.
Note :
Moment of inertia does not change if the mass :
(i) is shifted parallel to the axis of the rotation
(ii) is rotated with constant radius about axis of rotation
2.1 Moment of Inertia of a Single Particle

For a very simple case the moment of inertia of a single particle about an axis is given by,
I = mr2 ...(i)
Here, m is the mass of the particle and r its distance from the axis under consideration.
2.2 Moment of Inertia of a System of Particles
The moment of inertia of a system of particles about an axis is given by,


where ri is the perpendicular distance from the axis to the ith particle, which has a mass mi.
Ex.1 Two heavy particles having masses m1 & m2 are situated in a plane perpendicular to line AB at a distance of r1 and r2 respectively.

(i) What is the moment of inertia of the system about axis AB?
(ii) What is the moment of inertia of the system about an axis passing through m1 and perpendicular to the line joining m1 and m2 ?
(iii) What is the moment of inertia of the system about an axis passing through m1 and m2?
Sol. (i) Moment of inertia of particle on left is I1 = m1r12.
Moment of Inertia of particle on right is I2 = m2r22.
Moment of Inertia of the system about AB is
I = I1+ I2 = m1r12 + m2r22
(ii) Moment of inertia of particle on left is I1 = 0
Moment of Inertia of the system about CD is
I = I1 + I2 = 0 + m2(r1 + r2)2
(iii) Moment of inertia of particle on left is I1 = 0
Moment of inertia of particle on right is I2 = 0
Moment of Inertia of the system about EF is
I = I1 + I2 = 0 + 0
Ex.2 Three light rods, each of length 2l, are joined together to form a triangle. Three particles A, B, C of masses m, 2m, 3m are fixed to the vertices of the triangle. Find the moment of inertia of the resulting body about
(a) an axis through A perpendicular to the plane ABC,
(b) an axis passing through A and the midpoint of BC.
Sol.
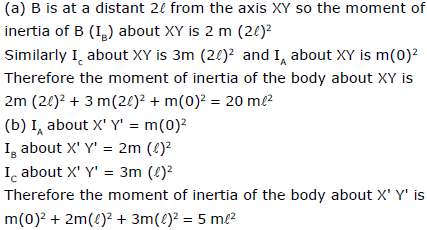


Ex.3 Four particles each of mass m are kept at the four corners of a square of edge a. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the centre of the square.
Sol.
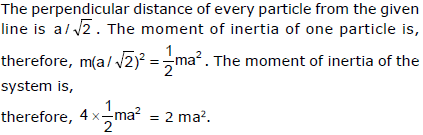

Moment of Inertia of Rigid Bodies - System of Particles and Rotational Motion, Class 11, Physics
2.3 Moment of Inertia of Rigid Bodies
For a continuous mass distribution such as found in a rigid body, we replace the summation of  by an integral. If the system is divided into infinitesimal element of mass dm and if r is the distance from a mass element to the axis of rotation, the moment of inertia is,
by an integral. If the system is divided into infinitesimal element of mass dm and if r is the distance from a mass element to the axis of rotation, the moment of inertia is,
I = 

where the integral is taken over the system.
(A) Uniform rod about a perpendicular bisector
Consider a uniform rod of mass M and length l figure and suppose the moment of inertia is to be calculated about the bisector AB. Take the origin at the middle point O of the rod. Consider the element of the rod between a distance x and x + dx from the origin. As the rod is uniform,

When x = - l/2, the element is at the left end of the rod. As x is changed from - l/2 to l/2, the elements cover the whole rod.
Thus, the moment of inertia of the entire rod about AB is

(B) Moment of inertia of a rectangular plate about a line parallel to an edge and passing through the centre
The situation is shown in figure. Draw a line parallel to AB at a distance x from it and another at a distance x + dx. We can take the strip enclosed between the two lines as the small element.

It is "small" because the perpendiculars from different points of the strip to AB differ by not more than dx. As the plate is uniform, its mass per unit area = 
Mass of the strip =  .
.
The perpendicular distance of the strip from AB = x.
The moment of inertia of the strip about AB = dI =  . The moment of inertia of the given plate is, therefore,
. The moment of inertia of the given plate is, therefore,

The moment of inertia of the plate about the line parallel to the other edge and passing through the centre may be obtained from the above formula by replacing l by b and thus,
 .
.
(C) Moment of inertia of a circular ring about its axis (the line perpendicular to the plane of the ring through its centre)
Suppose the radius of the ring is R and its mass is M. As all the elements of the ring are at the same perpendicular distance R from the axis, the moment of inertia of the ring is
 .
.
(D) Moment of inertia of a uniform circular plate about its axis
Let the mass of the plate be M and its radius R. The centre is at O and the axis OX is perpendicular to the plane of the plate.

Draw two concentric circles of radii x and x + dx, both centred at O and consider the area of the plate in between the two circles.
This part of the plate may be considered to be a circular ring of radius x. As the periphery of the ring is 2p x and its width is dx, the area of this elementary ring is 2pxdx. The area of the plate is p R2. As the plate is uniform,

Using the result obtained above for a circular ring, the moment of inertia of the elementary ring about OX is
.
The moment of inertia of the plate about OX is
.
(E) Moment of inertia of a hollow cylinder about its axis
Suppose the radius of the cylinder is R and its mass is M. As every element of this cylinder is at the same perpendicular distance R from the axis, the moment of inertia of the hollow cylinder about its axis is

(F) Moment of inertia of a uniform solid cylinder about its axis
Let the mass of the cylinder be M and its radius R. Draw two cylindrical surface of radii x and x + dx coaxial with the given cylinder. Consider the part of the cylinder in between the two surface. This part of the cylinder may be considered to be a hollow cylinder of radius x. The area of cross-section of the wall of this hollow cylinder is 2p x dx. If the length of the cylinder is l, the volume of the material of this elementary hollow cylinder is 2p x dxl.

Note that the formula does not depend on the length of the cylinder.
(G) Moment of inertia of a uniform hollow sphere about a diameter
Let M and R be the mass and the radius of the sphere, O its centre and OX the given axis (figure).

The mass is spread over the surface of the sphere and the inside is hollow.
Let us consider a radius OA of the sphere at an angle q with the axis OX and rotate this radius about OX. The point A traces a circle on the sphere. Now change q to q + dq and get another circle of somewhat larger radius on the sphere. The part of the sphere between these two circles, shown in the figure, forms a ring of radius R sinq. The width of this ring is Rdq and its periphery is 2pR sinq. Hence,
the area of the ring = 
Mass per unit area of the sphere .
.
The mass of the ring 
The moment of inertia of this elemental ring about OX is


As q increases from 0 to p, the elemental rings cover the whole spherical surface. The moment of inertia of the hollow sphere is, therefore,



(H) Moment of inertia of a uniform solid sphere about a diameter
Let M and R be the mass and radius of the given solid sphere. Let O be centre and OX the given axis. Draw two spheres of radii x and x + dx concentric with the given solid sphere. The thin spherical shell trapped between these spheres may be treated as a hollow sphere of radius x.

The mass per unit volume of the solid sphere
= 
The thin hollow sphere considered above has a surface area 4px2 and thickness dx. Its volume is

Its moment of inertia about the diameter OX is, therefore,
dl =  x2 =
x2 = 
If x = 0, the shell is formed at the centre of the solid sphere. As x increases from 0 to R, the shells cover the whole solid sphere.
The moment of inertia of the solid sphere about OX is, therefore,
I =  =
=  .
.
Ex.4 Find the moment of Inertia of a cuboid along the axis as shown in the figure.

Sol. After compressing the cuboid parallel to the axis I =
Theorems of Moment of Inertia - System of Particles and Rotational Motion, Class 11, Physics
3. Theorems of Moment of Inertia
There are two important theorems on moment of inertia, which, in some cases enable the moment of inertia of a body to be determined about an axis, if its moment of inertia about some other axis is known. Let us now discuss both of them.
3.1 Theorem of parallel axes
A very useful theorem, called the parallel axes theorem relates the moment of inertia of a rigid body about two parallel axes, one of which passes through the centre of mass.
Two such axes are shown in figure for a body of mass M.

If r is the distance between the axes and ICOM and I are the respective moments of inertia about them, these moments are related by,
I = ICOM + Mr2
* Theorem of parallel axis is applicable for any type of rigid body whether it is a two dimensional or three dimensional
Ex 5. Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertia of the system about an axis passing through its centre of mass and perpendicular to the plane of triangle.

Sol. Moment of inertia of rod BC about an axis perpendicular to plane of triangle ABC and passing through the mid-point of rod BC (i.e., D) is
I1 = 

Ex.6. Find the moment of inertia of a solid sphere of mass M and radius R about an axis XX shown in figure.


Ex.7. Consider a uniform rod of mass m and length 2l with two particles of mass m each at its ends. Let AB be a line perpendicular to the length of the rod passing through its centre. Find the moment of inertia of the system about AB.

3.2 Theorem of perpendicular axes
The theorem states that the moment of inertia of a plane lamina about an axis perpendicular to the plane of the lamina is equal to the sum of the moments of inertia of the lamina about two axes perpendicular to each other, in its own plane and intersecting each other, at the point where the perpendicular axis passes through it.
Let x and y axes be chosen in the plane of the body and z-axis perpendicular, to this plane, three axes being mutually perpendicular, then the theorem states that.

Iz = Ix + Iy
Important point in perpendicular axis theorem
(i) This theorem is applicable only for the plane bodies (two dimensional).
(ii) In theorem of perpendicular axes, all the three axes (x, y and z) intersect each other and this point may be any point on the plane of the body (it may even lie outside the body).
(iii) Intersection point may or may not be the centre of mass of the body.
Ex.8 Find the moment of inertia of uniform ring of mass M and radius R about a diameter.

Sol. Let AB and CD be two mutually perpendicular diameters of the ring. Take them ax X and Y-axes and the line perpendicular to the plane of the ring through the centre as the Z-axis. The moment of inertia of the ring about the Z-axis is I = MR2. As the ring is uniform, all of its diameter equivalent and so Ix = Iy, From perpendicular axes theorem,
Iz = Ix + Iy Hence Ix =  =
= 
Similarly, the moment of inertia of a uniform disc about a diameter is MR2/4
Ex.9 Two uniform identical rods each of mass M and length l are joined to form a cross as shown in figure. Find the moment of inertia of the cross about a bisector as shown dotted in the figure.

Sol. Consider the line perpendicular to the plane of the figure through the centre of the cross. The moment of inertia of each rod about this line is  and hence the moment of inertia of the cross is
and hence the moment of inertia of the cross is  . The moment of inertia of the cross about the two bisector are equal by symmetry and according to the theorem of perpendicular axes, the moment of inertia of the cross about the bisector is
. The moment of inertia of the cross about the two bisector are equal by symmetry and according to the theorem of perpendicular axes, the moment of inertia of the cross about the bisector is  .
.
Ex.10 In the figure shown find moment of inertia of a plate having mass M, length l and width b about axis 1,2,3 and 4. Assume that C is centre and mass is uniformly distributed

Sol. Moment of inertia of the plate about axis 1 (by taking rods perpendicular to axis 1)
l1 = Mb2/3
Moment of inertia of the plate about axis 2 (by taking rods perpendicular to axis 2)
I2 = Ml2/12
Moment of inertia of the plate about axis 3 (by taking rods perpendicular to axis 3)

Moment of inertia of the plate about axis 4(by taking rods perpendicular to axis 4)
I4 = Ml2/3
3.3 Moment of Inertia of Compound Bodies
Consider two bodies A and B, rigidly joined together. The moment of inertia of this compound
body, about an axis XY, is required. If IA is the moment of inertia of body A about XY. IB is the moment of inertia of body B about XY.Then, moment of Inertia of compound body I = IA + IB
Extending this argument to cover any number of bodies rigidly joined together, we see that the moment of inertia of the compound body, about a specified axis, is the sum of the moments of inertia of the separate parts of the body about the same axis.

Ex.11 Two rods each having length l and mass m joined together at point B as shown in figure.Then findout moment of inertia about axis passing thorugh A and perpendicular to the plane of page as shown in figure.

Sol. We find the resultant moment of inertia I by dividing in two parts such as
I = M.I of rod AB about A + M.I of rod BC about A
I = I1 + I2 ... (1)
first calculate I1 :

I1 =  ...(2)
...(2)

4. Cavity Problems :
Ex.12 A uniform disc having radius 2R and mass density s as shown in figure. If a small disc of radius R is cut from the disc as shown. Then find out the moment of inertia of remaining disc around the axis that passes through O and is perpendicular to the plane of the page.

Sol. We assume that in remaning part a disc of radius R and mass density ± s is placed. Then
 º
º  +
+ 
Total Moment of Inertia I = I1 + I2
I1 = 
I1 =  = 8 p s R4
= 8 p s R4
To calculate I2 we use parallel axis theorem.
I2 = ICM + M2R2
I2 =  + M2R2
+ M2R2
I2 =  =
=  I2 =
I2 = 
Now I = I1 + I2
I =  I =
I = 
Ex.13 A uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.

Sol. Let the mass per unit area of the material of disc be s. Now the empty space can be considered as having density - s and s.
Now I0 = Is + I- s

5. TORQUE :
Torque represents the capability of a force to produce change in the rotational motion of the body

5.1 Torque about point :
Torque of force  about a point
about a point 
where  = force applied
= force applied
P = point of application of force
Q = point about which we want to calculate the torque.
 = position vector of the point of application of force from the point about which we want to determine the torque.
= position vector of the point of application of force from the point about which we want to determine the torque.
 =
=  =
= 
where q = angle between the direction of force and the position vector of P wrt. Q.
 = perpendicular distance of line of action of force from point Q.
= perpendicular distance of line of action of force from point Q.
 = force arm
= force arm
SI unit to torque is Nm
Torque is a vector quantity and its direction is determined using right hand thumb rule.
Ex.14 A particle of mass M is released in vertical plane from a point P at x = x0 on the x-axis it falls vertically along the y-axis. Find the torque t acting on the particle at a time t about origin?
Sol.

Torque is produced by the force of gravity

or 
Ex.15 Calculate the total torque acting on the body shown in figure about the point O

Sol.

t0 = 15sin37 × 6  + 20 sin 30° × 4
+ 20 sin 30° × 4 - 10 × 4
- 10 × 4
= 54 + 40 - 40 = 54 N-cm
t0 = 0.54 N-m
Ex.16 A particle having mass m is projected with a velocity v0 from a point P on a horizontal ground making an angle q with horizontal. Find out the torque about the point of projection acting on the particle when

(a) it is at its maximum height ?
(b) It is just about to hit the ground back ?
Sol.

(a) Particle is at maximum height then t about point P is 
F = mg ; 
⇒tP =  =
= 
 =
= 
(b)

when particle is at point Q then t about point P is 
 ; F = mg
; F = mg
 = mg
= mg
Ex.17 In the previous question, during the motion of particle from P to Q. Torque of gravitational force about P is :
(A) increasing
(B) decreasing
(C) remains constant
(D) first increasing then decreasing
Sol. Torque of gravitational force about P is increasing because  is increasing from O to R. (Range)
is increasing from O to R. (Range)
5.2 Torque about axis :

where  = torque acting on the body about the axis of rotation
= torque acting on the body about the axis of rotation
 = position vector of the point of application of force about the axis of rotation.
= position vector of the point of application of force about the axis of rotation.
 = force applied on the body.
= force applied on the body.

To understand the concept of torque about axis we take a general example which comes out in daily life. Figure shows a door ABCD.

Which can rotate about axis AB. Now if we apply force. F at point. in inward direction then tAB = r F and direction of this tAB is along y axis from right hand thumb rule. Which is parallel to AB so gives the resultant torque.
Now we apply force at point C in the direction as shown figure. At this time are perpendicular to each other which gives

But door can't move when force is applied in this direction because the direction of  is perpendicular to AB according to right hand thumb rule.
is perpendicular to AB according to right hand thumb rule.
So there is no component of t along AB which gives 
Now conclude Torque about axis is the component of  parallel to axis of rotation.
parallel to axis of rotation.
Note : The direction of torque is calculated using right hand thumb rule and it is always perpendicular to the plane of rotation of the body.

If F1 or F2 is applied to body, body revolves in anti-clockwise direction and F3 makes body revolve in clockwise direction. If all three are applied.
 (in anti-clockwise direction)
(in anti-clockwise direction)
===================================================
Equilibrium of a Rigid Body - System of Particles and Rotational Motion, Class 11, Physics
6. Body is in equilibrium : -
We can say rigid body is in equillibrium when it is in

Note :
(i) If net force on the body is zero then net torque of the forces may or may not be zero.
example.
A pair of forces each of same magnitude and acting in opposite direction on the rod.

(2) If net force on the body is zero then torque of the forces about each and every point is same
t about B 

t about C 
Ex.18 Determine the point of application of third force for which body is in equillibrium when forces of 20 N & 30 N are acting on the rod as shown in figure

Sol. Let the magnitude of third force is F, is applied in upward direction then the body is in the equilibrium when
(i)  (Translational Equillibrium)
(Translational Equillibrium)
⇒ 20 + F = 30 ⇒ F = 10 N
So the body is in translational equilibrium when 10 N force act on it in upward direction.
(ii)

so 10 N force is applied at 70 cm from point A to keep the body in equilibrium.
Ex.19 Determine the point of application of force, when forces are acting on the rod as shown in figure.

Sol. Since the body is in equillibrium so we conclude  and torque about any point is zero i.e.,
and torque about any point is zero i.e.,

Let us assume that we apply F force downward at A angle q from the horizontal, at x distance from B

Ex.20 A uniform rod length l, mass m is hung from two strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings ?

Sol. Let us assume that tension in left and right string is TA and TB respectively. Then

Ladder Problems :
Ex.21 A stationary uniform rod of mass `m', length `l' leans against a smooth vertical wall making an angle q with rough horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod?

Sol. As the rod is stationary so the linear acceleration and angular acceleration of rod is zero.

Ex.22 The ladder shown in figure has negligible mass and rests on a frictionless floor. The crossbar connects the two legs of the ladder at the middle. The angle between the two legs is 60°. The fat person sitting on the ladder has a mass of 80 kg. Find the contanct force exerted by the floor on each leg and the tension in the crossbar.

Sol. The forces acting on different parts are shown in figure. Consider the vertical equilibrium of "the ladder plus the person" system. The forces acting on this system are its weight (80 kg) g and the contact force N + N = 2 N due to the floor. Thus

Next consider the equilibrium of the left leg of the ladder. Taking torques of the forces acting on it about the upper end,

Ex.23 A thin plank of mass m and length l is pivoted at one end and it is held stationary in horizontal position by means of a light thread as shown in the figure then find out the force on the pivot.

Sol. Free body diagram of the plank is shown in figure.


Ex.24 A square plate is hinged as shown in figure and it is held stationary by means of a light thread as shown in figure. Then find out force exerted by the hinge.

Sol.

7. Relation between torque and angular acceleration
The angular acceleration of a rigid body is directly proportional to the sum of the torque components along the axis of rotation. The proportionality constant is the inverse of the moment of inertia about that axis, or

Thus, for a rigid body we have the rotational analog of Newton's second law ;
 ...(iii)
...(iii)
Following two points are important regarding the above equation.
(i) The above equation is valid only for rigid bodies. If the body is not rigid like a rotating tank of water, the angular acceleration a is different for different particles.
(ii) The sum St in the above equation includes only the torques of the external forces, because all the internal torques add to zero.
Ex.25 A uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H.

(i) Find angular acceleration a of the rod just after it is released from initial horizontal position from rest?
(ii) Calculate the acceleration (tangential and radial) of point A at this moment.

Ex.26 A uniform rod of mass m and length l hinged at point H can rotate in vertical plane about a smooth horizontal axis. Find force exerted by the hinge just after the rod is released from rest, from an initial position making an angle of 37° with horizontal ?

Sol. Just After releasing at 37º from horizontal F.B.D. of plank


⇒ a =  rad/sec2
rad/sec2
Now Tangential acceleration of centre of mass
at = a. =
= 
just after release vcm = 0 ⇒ ar = 0
Now resolving of at in horizontal and vertical direction as shwon in figure


from Fnet = ma in both horizontal and vertical direction
N2=  ⇒ N1 =
⇒ N1 = 
Now R = 
R = 
Pulley Block system
If there is friction between pulley and string and pulley have some mass then tension is different on two sides of the pulley.
Reason : To understand this concept we take a pulley block system as shown in figure.

Let us assume that tension induced in part AB of the string is T1 and block M move downward. If friction is present between pulley and string then it opposes the relative slipping between pulley and string, take two point e and f on pulley and string respectively. If friction is there then due to this, both points wants to move together. So friction force act on e and d in the direction as shown is figure

Ex.27 The pulley shown in figure has moment of inertia l about its axis and radius R. Find the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
Sol. Suppose the tension in the left string is T1 and that in the right string is T2. Suppose the block of mass M goes down with an acceleration a and the other block moves up with the same acceleration. This is also the tangential acceleration of the rim of the wheel as the string does not slip over the rim.


Substituting for T1 and T2 from equations (i) and (ii) in equation (iii)

========================================================
Angular Momentum - System of Particles and Rotational Motion, Class 11, Physics
8. Angular Momentum
8.1 Angular momentum of a particle about a point.


 = position of vector of particle with respect to point about which
= position of vector of particle with respect to point about which
angular momentum is to be calculated.
θ = angle between vectors 
 = perpendicular distance of line of motion of particle from point O.
= perpendicular distance of line of motion of particle from point O.
 = perpendicular component of momentum.
= perpendicular component of momentum.
SI unit of angular momentum is kgm2/sec.
Ex.28 A particle of mass m is moving along the line y = b, z = 0 with constant speed v. State whether the angular momentum of particle about origin is increasing, decreasing or constant.


Direction of  also remains the same. Therefore, angular momentum of particle about origin remains constant with due course of time.
also remains the same. Therefore, angular momentum of particle about origin remains constant with due course of time.
Note : In this problem  is increasing, q is decreasing but r sin q, i.e., b remains constant. Hence, the angular momentum remains constant.
is increasing, q is decreasing but r sin q, i.e., b remains constant. Hence, the angular momentum remains constant.
Ex.29 A particle of mass m is projected with velocity v at an angle q with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
Sol. At the highest point it has only horizontal velocity vx = v cos q. Length of the perpendicular to the horizontal velocity from 'O' is the maximum height, where

⇒ Angular momentum L = 

8.2 Angular Momentum of a rigid body rotating about a fixed axis
Suppose a particle P of mass m is going in a circle of radius r and at some instant the speed of the particle is v. For finding the angular momentum of the particle about the axis of rotation, the origin may be chosen anywhere on the axis. We choose it at the centre of the circle. In this case  are perpendicular to each other
are perpendicular to each other  and is along the axis. Thus, component of along the axis is mvr itself. The angular momentum of the whole rigid body about AB is the sum of components of all particles, i.e.,
and is along the axis. Thus, component of along the axis is mvr itself. The angular momentum of the whole rigid body about AB is the sum of components of all particles, i.e.,
L = 

Here, I is the moment of inertia of the rigid body about AB.
Note : Angular momentum about axis is the component of  along the axis. In most of the cases angular momentum about axis is Iω.
along the axis. In most of the cases angular momentum about axis is Iω.
Ex.30 Two small balls A and B, each of mass m, are attached rigidly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed w. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
Sol.

Consider the situation shown in figure. The velocity of the ball A with respet to the centre O is v =  .
.
The angular momentum of the ball with respect to the axis is
L1 = mvr =  =
=  mwd2. The same the angular momentum L2 of the second ball. The angular momentum of the system is equal to sum of these two angular momenta i.e., L = 1/2 mwd2.
mwd2. The same the angular momentum L2 of the second ball. The angular momentum of the system is equal to sum of these two angular momenta i.e., L = 1/2 mwd2.
9. Conservation of Angular momentum :
The time rate of change of angular momentum of a particle about some referenence point in an inertial frame of reference is equal to the net torques acting on it.
or  ....(i)
....(i)
Now, suppose that  , then
, then  , so that
, so that  = constant.
= constant.
"When the resultant external torque acting on a system is zero, the total vector angular momentum of the system remains constant. This is the principle of the conservation of angular momentum.
For a rigid body rotating about an axis (the z-axis, say) that is fixed in an inertial reference frame, we have
Lz = Iw
It is possible for the moment of inertia I of a rotating body to change by rearrangement of its parts. If no net external torque acts, then Lz must remains constant and if I does change, there must be a compensating change in w. The principle of conservation of angular momentum in this case is expressed.
Iw = constant.
Ex.31 A wheel of moment of inertia I and radius R is rotating about its axis at an angular speed w0. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
Sol. Net external torque on the system is zero. Therefore, angular momentum will remain conserved. Thus,

Note :

Comments on Linear Momentum :
In case I : Linear momentum is not conserved just before and just after collision because during collision hinge force act as an external force.
In case II : Linear momentum is conserved just before and just after collision because no external force on the string.
Comments on Angular Momentum :
In case I : Hinge force acts at an external force during collision but except point A all the other reference point given  . So angular momentum is conserved only for point A.
. So angular momentum is conserved only for point A.
In case II : angular momentum is conserved at all points in the world.
Ex.32 A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod in-elastically at its free end. Find out the angular velocity of the rod just after collision?

Sol. Angular momentum is conserved about H because no external force is present in horizontal plane which is producing torque about H.
Ex.33 A uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod and sticks to it at a distance of 3l/4 from hinge point. Find out the angular velocity of the rod just after collision?

Sol.

from angular momentum conservation about H
initial angular momentum = final angular momentum

Ex.34 A uniform rod AB of mass m and length 5a is free to rotate on a smooth horizontal table about a pivot through P, a point on AB such that AP = a. A particle of mass 2m moving on the table strikes AB perpendicularly at the point 2a from P with speed v, the rod being at rest. If the coefficient of restitution between them is  , find their speeds immediately after impact.
, find their speeds immediately after impact.
Sol. Let the point of impact be Q so that
PQ = 2a
Let P be the point of pivot that AP = a

Let the velocities of point, Q and the particle after impact be vq and vp respectively then from momentum conservation about point P.
Li = Lf



Ex.35 A person of mass m stands at the edge of a circular platform of radius R and moment of inertia. A platform is at rest initially. But the platform rotate when the person jumps off from the platform tangentially with velocity u with respect to platfrom. Determine the angular velocity of the platform.
Sol. Let the angular velocity of platform is w. Then the velocity of person with respect to ground v.




Ex.36 Consider the situation of previous example. If the platform is rotating intially with angular velocity w0 and then person jumps off tangentially. Determine the new angular velocity of the platform.
Sol. Let the angular velocity of platfrom after jumps off the mass is w. Then velocity Of man.



10. Angular Impulse
The angular impulse of a torque in a given time interval is defined as 
Here,  is the resultant torque acting on the body. Further, since
is the resultant torque acting on the body. Further, since

Thus, the angular impulse of the resultant torque is equal to the change in angular momentum. Let us take few examples based on the angular impulse.
Ex.37 Figure shows two cylinders of radii r1 and r2 having moments of inertia I1 and I2 about their respective axes. Initially, the cylinders rotate about their axes with angular speeds w1 and w2 as shown in the figure. The cylinders are moved closer to touch each other keeping the axes parallel. The cylinders first slip over each other at the contact but the slipping finally ceases due to the friction between them. Find the angular speeds of the cylinders after the slipping ceases.

Sol. When slipping ceases, the linear speeds of the points of contact of the two cylinders will be equal. If  and
and  be the respective angular speeds, we have
be the respective angular speeds, we have
 .....(i)
.....(i)
The change in the angular speed is brought about by the frictional force which acts as long as the slipping exists. If this force f acts for a time t, the torque on the first cylinder is fr1 and that on the second is f r2. Assuming w1 r1 > w2 r2, the corresponding angular impluses are - f r1 t and f r2 t. We, therefore, have

Kinetic Energy of a rigid body rotating about a fixed axis.
Suppose a rigid body is rotating about a fixed axis with angular speed w.
Then, kinetic energy of the rigid body will be :


Thus, KE = 
Sometimes it is called the rotational kinetic energy.
Ex.38 A uniform rod of mass m and length l is kept vertical with the lower end clamped. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest position. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?
Sol. As the rod reaches its lowest position, the centre of mass is lowered by a distance l. Its gravitational potential energy is decreased by mgl. As no energy is lost against friction, this should be equal to the increase in the kinetic energy. As the rotation occurs about the horizontal axis through the clamped end, the moment of inertia is I = m l2/3. Thus,


=========================================================
Dynamics of a Rotational Motion - System of Particles and Rotational Motion, Class 11, Physics
11. Combined Translational and Rotational motion of a rigid body :
We have already learnt about translational motion caused by a force and rotational motion about a fixed axis caused by a torque. Now we are going to discuss a motion in which body undergoes translational as well as rotational motion. Rolling is an example of such motion. If the axis of rotation is moving then the motion is combined translational and rotational motion.
To understand the concept of combined translational and rotational motion we consider a uniform disc rolling on a horizontal surface. Velocity of its centre of mass is Vcom and its angular speed is w as shown in figure.

Let us take a point A on the disc and concentrate on its motion.
Path of point A with respect to ground will be a cycloid as shown in figure.

Motion of point A with respect to center of mass is pure rotational while center of mass itself is moving in a straight line. So for the analysis of rolling motion we deal translational motion seperately and rotational motion seperately and then we combine the result to analyses the over all motion.
The velocity of any point A on the rigid body can be obtained as


 in the direction
in the direction  to line OA
to line OA
Thus, the velocity of point A is the vector sum of  and
and  as shown in figure
as shown in figure

Important points in combined Rotational + translation motion :
1. Velocity of any point of the rigid body in combined R + T motion is the vector sum of
v(velocity of centre of mass) and rw
for example
A disc of radius r has linear velocity v and angular velocity w as shown in figure then find velocity of point A. B, C, D on the disc

We divide our problem in two parts
(1) Pure Rotational + (2) Pure Translational
about centre of mass.
 +
+ 
Then combine the result of above both

2. In combined rotational and translational motion angular velocity of any point of a rigid body with respect to other point in the rigid body is always same.
For example :
 (v = rw)
(v = rw) 
Now for wDA wDA =  =
= 

3. Distance moved by the centre of mass of the rigid body in one full rotation is 2pR.

This can be shown as under :
In one rotation angular displacement q = 2p = wt

4. The speed of a point on the circumference of the body at any instant t is 2Rw sin
Proof :


5. The path of a point on circumference is a cycloid and the distance moved by this point in one full rotation is 8R.

In the figure, the dotted line is a cycloid and the distance A1 A2 ......A5 is 8R. This can be proved as under.
According to point (3), speed of point A at any moment is,

Distance moved by A in time dt is,


Therefore, total distance moved in one full rotation is,

On integration we get, s = 8R
6. x and y coordinates of the bottommost point at any time t.
At time t the bottommost point will rotate an angle q = wt with respect to the centre of the disc C. The centre C will travel a distance s = vt.


11.1 Angular momentum of a rigid body in combined rotation and translation

Let O be a fixed point in an inertial frame of reference. Angular momentum of the body about O is.

The first term  represents the angular momentum of the body as seen from the centre of mass frame. The second term
represents the angular momentum of the body as seen from the centre of mass frame. The second term  equals the angular momentum of centre of mass about point O.
equals the angular momentum of centre of mass about point O.
Ex.39 A circular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed  in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottommost point O of the disc.
in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottommost point O of the disc.
Sol.



11.2 Kinetic Energy of a Rolling Body
If a body of mass M is rolling on a plane such that velocity of its centre of mass is V and its angular speed is w, its kinetic energy is given by
KE = 
I is moment of inertia of body about axis passing through centre of mass.
In case of rolling without slipping.
KE =  +
+  [ v = wR]
[ v = wR]
 =
= 
Ic is moment of inertia of the body about the axis passing through point of contact.
Ex.40 A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a/4 from the centre and stops after the collision. Find (a) the velocity of the centre of the rod and (b) the angular velocity of the rod about its centre just after the collision.
Sol.

The situation is shown in figure. Consider the rod and the particle together as the system. As there is no external resultant force, the linear momentum of the system will remain constant. Also there is no resultant external torque on the system and so the angular momentum of the system about any line will remain constant.
Suppose the velocity of the centre of the rod is V and the angular velocity about the centre is w.
(a) The linear momentum before the collision is mv and that after the collision is MV. Thus,
mv = MV, or V = 
(b) Let A be the centre of the rod when it is at rest. Let AB be the line perpendicular to the plane of the figure. Consider the angular momentum of "the rod plus the particle" system about AB. Initially the rod is at rest. The angular momentum of the particle about AB is
L = mv(a/4)

Ex.41 A uniform rod of length l lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
(a) The moment of inertia of the system about the vertical axis passing through the centre of mass C after the collision.
(b) The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
Sol. Figure shows the situation of system just before and just after collision.
Initially the centre of mass of the rod is at point O. After collision when the particle sticks to the rod. Centre of mass is shifted from point O to C as shown in figure. Now the system is rotated about axis passing through C

Now from linear momentum conservation

(a) Let us assume that moment of inertia of the system about C is 1. Then 

 ⇒
⇒ 
(b) From Angular momentum conservation about A

11.3 Acceleration of a point on the circumference of the body in R + T motion :
(A) Both w & v are constant :

(B) When w is constant and v is variable.


So acceleration of different point on the body is given by following figure.
 +
+  =
= 
(C) When w is variable and v is constant :


So acceleration of different point on the body is given by following way
 º
º 
(D) When both w & v are variable :
 →
→ 
Now the net acceleration of different points on the rigid body is given by following way.



Ex.42 A force F acts at the centre of a thin spherical shell of mass m and radius R.
Find the acceleration of the shell if the surface is smooth.
Sol.


Ex.43 In a previous problem if force F applied at a distance x above the centre then find out linear and angular acceleation.
Sol.

Ex.44 A rigid body of mass m and radius r starts coming down an inclined plane of inclination q. Then find out the acceleration of centre of mass if friciton is absent.
Sol.

Friction is absent so body is moving down the incline with out rolling so acceleration of centre of mass is g sinq
12. Uniform Pure Rolling
Pure rolling means no relative motion (or no slipping at point of contact between two bodies.)
For example, consider a disc of radius R moving with linear velocity v and angular velocity w on a horizontal ground. The disc is said to be moving without slipping if velocities of points P and Q (shown in figure b) are equal, i.e.,

If vp > vQ or v > Rw, the motion is said to be forward slipping and if vp < vQ < Rw, the motion is said to be backward slipping.
Now, suppose an external force is applied to the rigid body, the motion will no longer remain uniform. The condition of pure rolling on a stationary ground is,
 is the condition of pure rolling on a stationary ground. Sometime it is simply said rolling.
is the condition of pure rolling on a stationary ground. Sometime it is simply said rolling.
Note : We can represent the moment of inertia of a different rigid body in a following way.
I = CMR2
 C =
C =  for Hollow sphere (H.S) , C =
for Hollow sphere (H.S) , C =  for solid sphere (S.S)
for solid sphere (S.S)
Ex.45 A rigid body I = CMR2 is set into a motion on a rough horizontal surface with a linear speed v0 in the forward direction at time t = 0 as shown in figure. After what time slipping finally stop and pure rolling starts. Find the linear speed of the body after it starts pure rolling on the surface.

Sol. According to the given condition in problem the point P in the body move with speed v0 while the point Q on the ground is at rest. So the friciton acts on the body is in backward direction which gives the resultant torque on the body and increase the angualr speed w as shown in figure.



As shown in above figure initially v > Rw so forward slipping takes place. After introducing the friciton speed decreases and w increases and at time t = t the relation v = r w is satisfied. Therefore pure rolling starts. Initially the friciton is kinetic untill the motion is in slipping condition. Afterwards at v = rw fricition is static. We divide the above problem in two parts.
(1) Translational Motion :

(2) Rotational Motion :

Equation (5) gives the linear speed at pure rolling situation.
Alternate solution :
Net torque on the body about the bottom most point A is zero. Therefore angular momentum of the body will remain conserved about the bottom most point

Ex.46 In the previous problem take rigid body a solid cylinder then find out the work done by friciton from time t = 0 to t = t 
Sol. Let us suppose that in between time t = 0 to t = t cylinder displaced s.

Translational work done by friciton + Rotational work Done by friciton
Now calculate each type of work done one by one
(A) Translational work done by friciton :

(B) Rotational W.D. by friciton :

(C) So total W.D. by friciton W = Wf T + Wf R =

Alternative Method :
from work - Energy Theorem
work done by friciton = change in kinetic energy

To calculate work done mostly prefer alternative method.
Ex.47 A solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed w0 and no linear velocity. If the coefficient of friciton is μ, find the linear velocity v and angular velocity w at the end of slipping.

Sol. m be the mass of the sphere.
Since, it is a case of backward slipping, force of friction is in forward direction. Limiting friciton will act in this case.
Net torque on the sphere about the bottommost point is zero. Therefore, angular momentum of the sphere will remain conserved about the bottommost point.


12.1 Pure rolling when force F act on a body :
Suppose a force F is applied at a distance x above the centre of a rigid body of radius R, mass M and moment of inertia CMR2 about an axis passing through the centre of mass. Now, the applied force F can produces by itself
(i) a linear acceleration a and
(ii) an angular acceleration a
If a = Ra, then there is no need of friction and force of friction f = 0,
If a < Ra, then to support the linear momentum the force of friciton f will act in forward direction,
Similarly, if a > Ra, then no support the angular motion the force of friciton will act in backward direction.
So, in this case force of friction will be either backward, forward or even zero also. It all depends on M, I and R. For calculation you choose any direction of friction. Let we assume it in forward direction.
Let, a = linear acceleration,

Ex.48 Consider the arrangment shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a massless, frictionless pulley to a falling weight. Determine the acceleration of the falling mass m in terms of only the mass of the cylinder M, the mass m and g.

Sol. Let T be the tension the string and f the force of (static) friction, between the cylinder and the surface
a1 = acceleration of centre of mas of cylinder towards right
a2 = downward acceleration of block m

We also have (for rolling without slipping)
a1 = Ra ...(v)
Solving these equations, we get 
Note : Work done by friction in pure rolling on a stationary ground is zero as the point of application of the force is at rest. Therefore, machanical energy can be conserved if all other dissipative forces are ignored.
12.2 Pure Rolling on an Inclined Plane:
A rigid body of radius R, and mass m is released at rest from height h on the incline whose inclination with horizontal is q and assume that friciton is sufficient for pure rolling then.


So body which have low value of C have greater acceleration.
value of C = 1 for circular ring (R)
C =  for circular disc (D) and solid cylinder (S.C.)
for circular disc (D) and solid cylinder (S.C.)
C =  for Hollow sphere (H.S)
for Hollow sphere (H.S)
C =  for solid sphere (S.S)
for solid sphere (S.S)
So, descending order of a
aS.S > aD = aS.C > aH.S. > aR
and order of time of descend is
ts.s < tD = ts.c < tH.S < tR
Kinetic Eneregy : Work done by friction in pure rolling is zero. Therefore,
Increase in kinetic energy = change in potential energy ⇒ K.E. = mgh
i.e., kinetic energy is constant for all rigid body rolling down the incline.
Requirement of Friction :
From eq. ...(2)
f = Cma
 ...(3)
...(3)
from eq. (3) as the value of C increase requirement of friciton is increases.
Ex.49 A cylinder of mass M is suspended through two strings wrapped around it as shown in figure. Find the tension in the string and the speed of the cylinder as it falls through a distance h.
Sol. The portion of the strings between ceiling and cylinder are at rest. Hence the points of the cylinder where the strings leave it are at rest also. The cylinder is thus rolling without slipping on the strings. Suppose the centre of cylinder falls with an acceleration a. The angular acceleration of cylinder about its axis given by

As the centre of cylinder starts moving from rest, the velocity after it has fallen a height h is given by
v2 = 2 or v =
or v = 
Ex.50 A thin massless thread is wound on a reel of mass 3kg and moment of inertia 0.6 kg-m2. The hub radius is R = 10 cm and peripheral radius is 2R = 20 cm. The reel is placed on a rough table and the friction is enough to prevent slipping. Find the acceleration of the centre of reel and of hanging mass of 1 kg.

Sol. Let, a1 = acceleration of centre of mass of reel
a2 = acceleration of 1 kg block
α = angular acceleration of reel (clockwise)
T = tension in the string
and f = force of friction
Free body diagram of reel is as shown below :
(only horizontal forces are shown).
Equations of motion are :


Ex.51 Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are ms and mk respectively.

Sol. The free body diagrams of the sphere and the plank are as shown below :

For plank : Linear acceleration


Ex.52 Find out the maximum height attained by the solid sphere on a friciton less track as shown in figure.

Sol. Let us assume that sphere attain a maximum height H on the track.

As the sphere move upward speed is decreased due to gravity but there is no force to change the w0 (friction less track). So from energy conservation
 = mg Hmax +
= mg Hmax +  , Hmax =
, Hmax = 
13. Toppling
You might have seen in your practical life that if a force F is applied to a block A of smaller width it is more likely to topple down, before sliding while if the same force F is applied to an another block B of broader base, chances of its sliding are more compared to its toppling. Have you ever throught why it happens so. To understand it better let us take an example.


Suppose a force F is applied at a height b above the base AE of the block. Further, suppose the friction f is sufficient to prevent sliding. In this case, if the normal reaction N also passes through C, then despite the fact that the block is in translational equilibium (F = f and N = mg), an unbalanced torque (due to the couple of forces F and f) is there. This torque has a tendency to topple the block about point E. To cancel the effect of this unbalanced torque the normal reaction N is shifted towards right a distance 'a' such that, net anticlockwise torque is equal to the net clockwise torque or

Fb = (mg) a
or a =


Now, as F or b (or both) are increased, distance a also increases. But it can not go beyond the right edge of the block. So, in extreme case (beyond which the block will topple down), the normal reaction passes through E as shown in figure.
Now, if F or b are further increased, the block will topple down. This is why the block having the broader base has less chances of toppling in comparison to a block of smaller base. Because the block of larger base has more margin for the normal reaction to shift.
Why the rolling is so easy on the ground.

Because in this case the normal reaction has zero margin to shift. so even if the body is in translational equilibrium (F = f, N = mg) an unbalanced torque is left behind and the body starts rolling clockwise. As soon as the body starts rolling the force of friction is so adjusted (both in magnitude and direction) that either the pure rolling starts (if friciton is sufficient enough) or the body starts sliding. Let us take few examples related to toppling.
Ex.53 A uniform block of height h and width a is placed on a rough inclined plane and the inclination of the plane to the horizontal is gradually increased. If m is the coefficient of friction then under condition the block will
(A) slide before toppling :

(B) Now suppose the friction f is sufficient to prevent sliding. Then we assume that N is shifted towards downward a distance x to prevent toppling Therefore. torque about O is zero.



14. Instantaneous Axis of Rotation
The combined effects of translation of the centre of mass and rotation about an axis through the centre of mass are equivalent to a pure rotation with the same angular speed about an axis passing through a point of zero velocity. Such an axis is called the instantaneous axis of rotation. (IAOR). This axis is always perpendicular to the plane used to represent the motion and the intersection of the axis with this plane defines the location of instantaneous centre of zero velocity (IC).

For example consider a wheel which rolls without slipping. In this case the point of contact with the ground has zero velocity. Hence, this point represents the IC for the wheel. If it is imagined that the wheel is momentarily pinned at this point, the velocity of any point on the wheel can be found using v = rw. Here r is the distance of the point from IC. Similarly, the kinetic energy of the body can be assumed to be pure rotational about IAOR or,


14.1 Location of the IC
If the location of the IC is unknown, it may be determined by using the fact that the relative position vector extending from the IC to a point is always perpendicular to the velocity of the point. Following three possibilities exist.
(i) Given the velocity of a point (normally the centre of mass) on the body and the angular velocity of the body
If v and w are known, the IC is located along the line drawn perpendicular to at P, such that the distance from P to IC is,  . Note that IC lie on that side of P which causes rotation about the IC, which is consistent with the direction of motion caused by and .
. Note that IC lie on that side of P which causes rotation about the IC, which is consistent with the direction of motion caused by and .

Ex.54 A rotating disc moves in the positive direction of the x-axis. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment the centre c of the disc was located at the point O after which it moved with constant velocity v while the disc started rotating counter clockwise with a constant angular acceleration a. The initial angular velocity is equal to zero.

Sol.

This is the desired x-y equation. This equation represents a rectangular hyperbola.
(ii) Given the lines of action of two non-parallel velocities
Consider the body shown in figure where the line of action of the velocities  and
and  are known. Draw perpendiculars at A and B to these lines of action. The point of intersection of these perpendiculars as shown locates the IC at the instant considered.
are known. Draw perpendiculars at A and B to these lines of action. The point of intersection of these perpendiculars as shown locates the IC at the instant considered.

(iii) Given the magnitude and direction of two parallel velocities
When the velocities of points A and B are parallel and have known magnitudes vA and vB then the location of the IC is determined by proportional triangles as shown in figure.


As a special case, if the body is translating, vA = vB and the IC would be located at infinity, in which case w = 0.
Ex.55 A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle q with horizontal.
Sol. As the floor is smooth, mechanical energy of the rod will remain conserved. Further, no horizontal force acts on the rod, hence the centre of mass moves vertically downwards in a straight line. Thus velocities of COM and the lower end B are in the direction shown in figure. The location of IC at this instant can be found by drawing perpendiculars to and at respective points. Now, the rod may be assumed to be in pure rotational motion about IAOR passing through IC with angular speed w.

Applying conservation of mechanical energy. Decrease in gravitational potential energy of the rod = increase in rotational kinetic energy about IAOR

FAQs on Rotational Motion, Chapter Notes, Class 11, Physics (IIT-JEE and AIPMT)
| 1. What is rotational motion? |  |
| 2. What are the units of angular velocity? |  |
| 3. How is the moment of inertia of an object calculated? |  |
| 4. What is the difference between torque and force? |  |
| 5. What is the relationship between angular acceleration and angular velocity? |  |






















