Straight Lines Class 11 Notes, Maths (IIT) PDF Download
Basic Terms Related to Straight Lines ,Class 11, Mathematics
Straight Lines
A. COORDINATE GEOMETRY
Coordinate Geometry is the unification of algebra and geometry in which algebra is used in the study of geometrical relations and geometrical figures are represented by means of equations. The most popular coordinate system is the rectangular Cartesian system. Coordinates of a point are the real variables associated in an order to describe its location in space. Here we consider the space to be two-dimensional. Through a point O, referred to as the origin, we take two mutually perpendicular lines XOX' and YOY' and call them x and y axes respectively. The position of a point is completely determined with reference to these axes by means of an ordered pair of real numbers (x, y) called the coordinates of P where |x | and | y | are the distances of the point P from the y-axis and the x-axis respectively, x is called the x-coordinate or the abscissa of P and y is called the y-coordinate or the ordinate of the point P.
(1) Distance between two points :
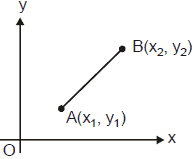
(a) Let A and B be two given points,whose coordinates are given by A(x1, y1) and B(x2 , y2) respectively.
Then AB =
(b) Distance of (x1, y1) from origin :
Note :- If two vertex A(x1, y1), B(x2, y2) are given then third vertex of equilateral triangle
C is
(2) Section formula :
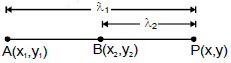
Coordinates of the point P dividing the join of two points A(x1, y1) and B(x2, y2) internally in the given ratio 
are P .
Coordinates of the point P dividing the join of two points A(x1, y1) and B(x2, y2) externally in the ratio of  are P
are P . In both the cases,
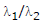 is positive.
is positive.
Notes :
(i) If the ratio, in which a given line segment is divided, is to be determined, then sometimes, for convenience (instead of taking the ratio  ), we take the ratio k : 1. If the value of k turns out to be positive, it is an internal division otherwise it is an external division.
), we take the ratio k : 1. If the value of k turns out to be positive, it is an internal division otherwise it is an external division.
(ii) The coordinates of the mid-point of the line-segment joining A(x1, y1) and B(x2, y2) are .
(3) Special points in a triangle with co-ordinates :
(a) Centroid (G) :
Definition : The point of concurrence of the medi ans of a triangle is called the centroid of the triangle.
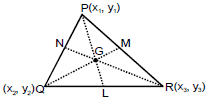
(i) G divides median into 2 : 1.
(ii) G always lies inside the triangle.
(iii) Co-ordinates of G is or
(b) Incentre (I) :
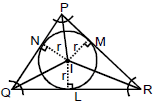
Definition : The point of concurrency of the internal bisectors of the angles of a triangle is called the incentre of the triangle.
(i) I always lies inside the triangle.
(ii) Internal angle bisector divides the base in the ratio of adjacent sides.
(iii) Co-ordinates of I is
where a, b, c are the lengths of the sides of the Δ
(c) Ex-centres (I1, I2, I3) :
Definition : The centre of the escribed circle which is opposite to vertices.
To get I1 (or I2 or I3) replace a by -a (b by -b or c by -c) in formula of coordinate of I
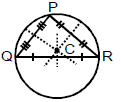
(d) Circumcentre (C) :
Definition : The point of concurrency of the perpendicular bisectors of the sides of a triangle is called circumcentre of the triangle.
(i) For acute angle Δ ⇒ lies inside
(ii) For obtuse angle Δ ⇒ lies outside
(iii) For right angle Δ ⇒ Mid point of hypotenuse
(iv) Co-ordinates of circumcentre is
(e) Orthocentre (O) :
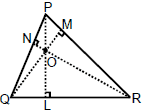
Definition : The point of concurrency of the altitudes of a triangle is called the orthocentre of the triangle.
(i) For acute angle Δ ⇒ lies inside
(ii) For obtuse angle Δ ⇒ lies outside
(iii) For right angle Δ ⇒ vertex at ^ar
(iv) Co-ordinates of orthocentre is
Notes :
(i) In any triangle O, G, C are collinear.
(ii) In any triangle G divides the line joining O & C in ratio 2 : 1.
(iii) In an equilateral triangle O, G, C, I are coincident.
(iv) In an isosceles triangle O, G, C, I are collinear.
(f) Harmonic Conjugate : If P is a point that divides AB internally in the ratio m1 : m2 and Q is another point which divides AB externally in the same ratio m1 : m2, then the point P and Q are said to be Harmonic conjugate to each other with respect to A and B.
i.e. AP , AB and AQ forms a HP ⇒ 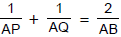
Note :- Internal and External angle bisector of an angle divides the base harmonically.
Ex.1 If midpoints of the sides of a triangle are (0, 4), (6, 4) and (6, 0), then find the vertices of triangle, centroid and circumcentre of triangle.
Sol. Let points A(x1, y1), B(x2, y2) and C(x3, y3) be vertices of ΔABC.
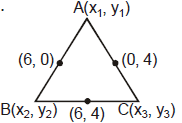
x1 + x3 = 0, y1 + y3 = 8
x2 + x3 = 12, y2 + y3 = 8
x1 + x2 = 12, y1 + y2 = 0
Solving we get A(0, 0), B (12, 0) and C(0, 8).
Hence DABC is right angled triangle 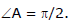
∴ Circumcentre is midpoint of hypotenuse which is (6, 4) itself and
centroid ≡ .
Ex.2 Prove that the incentre of the triangle whose vertices are given by A(x1, y1), B(x2, y2), C(x3, y3) is where a, b, and c are the sides opposite to the angles A, B and C respectively.
Sol. By geometry, we know that 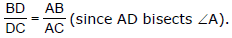
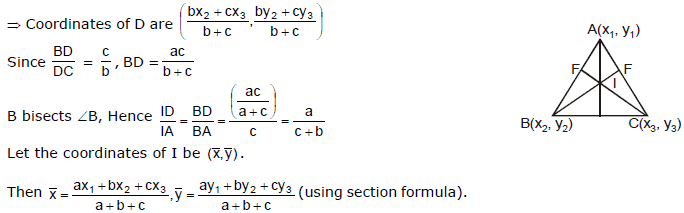
========================================================
Area of a Triangle - Straight Lines ,Class 11, Mathematics
B. AREA OF A TRIANGLE
Let (x1, y1), (x2, y2) and (x3, y3) respectively be the coordinates of the vertices A, B, C of a triangle ABC. Then the area of triangle ABC, is
...(1)
= ...(2)
While using formula (1) or (2). order of the points (x1, y1), (x2, y2) and (x3, y3) has not been taken into account. If we plot the points A(x1, y1), B (x2, y2) and C(x3, y3), then the area of the triangle as obtained by using formula (1) or (2) will be positive or negative as the points A, B, C are in anti-clockwise or clockwise directions.
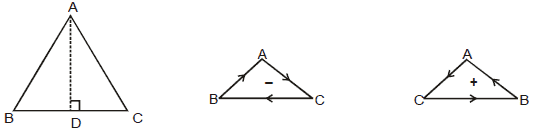
So, while finding the area of triangle ABC, we use the formula :
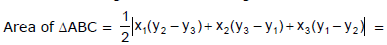
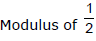
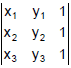
Notes :
(i) If three points (x1, y1), (x2, y2) and (x3, y3) are collinear, then
(ii) Equation of straight line passing through (x1, y1) and (x2, y2) is given by
(iii) In case of polygon with (x1, y1), (x2, y2) ............ (xn, yn) the area is given by
Ex.3 The vertices of quadrilateral in order are (-1, 4), (5, 6), (2, 9) and (x, x2). The area of the quadrilateral is units, then find the point (x, x2)
Sol.
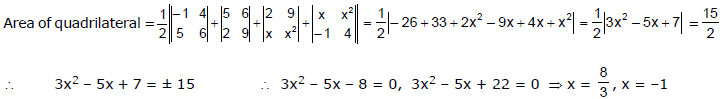 Hence point is
Hence point is or (-1, 1). But (-1, 1) will not form a quadrilateral as per given order of the points. Hence the required point is
(1) Locus : When a point moves in a plane under certain geometrical conditions, the point traces out a path. This path of a moving point is called its locus
Note : All those points which satisfy the given geometrical condition will definitely lie on the locus. But converse is not true always.
(2) Equation of Locus : The equation to a locus is the relation which exists between the coordinates of any point on the path, and which holds for no other point except those lying on the path.
(3) Procedure for finding the equation of the locus of a point
(i) If we are finding the equation of the locus of a point P, assign coordinates (h, k) to P.
(ii) Express the given conditions as equations in terms of the known quantities to facilitate calculations. We sometimes include some unknown quantities known as parameters.
(iii) Eliminate the parameters. so that the eliminate contains only h, k and known quantities.
(iv) Replace h by x, and k by y, in the eliminate. The resulting would be the equation of the locus of P.
(v) If x and y coordinates of the moving point are obtained in terms of a third variable t (called the parameter), eliminate t to obtain the relation in x and y and simplify this relation. This will give the required equation of locus.
Ex.4 Find the focus of the middle points of the segment of a line passing through the point of intersection of the lines ax + by + c = 0 and lx + my + n = 0 and intercepted between the axes
Sol. Any line (say L = 0) passing through the point of intersection of ax + by + c = 0 and lx + my + n = 0 is (ax + by + c) + λ (lx + my + n) = 0, where l is any real number.
Point of intersection of L = 0 with axes are and
Let the mid point be (h, k). Then and
Eliminating l, we get =
. The required locus is : 2(am - lb) = (lc - an) x + (nb - mc)y.
(4) Inclination of a line : Its a measure of the smallest non-negative angle which the line makes with +ve direction of the x-axis [angle being measured in anti-clockwise direction]. 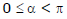
(5) Slope of the line : If the inclination of line is  then its slope is defined as tanθ and denoted by `m'
then its slope is defined as tanθ and denoted by `m'
(i) If θ = 0, then m = 0 i.e. line parallel to x-axis.
(ii) If θ = 90º, then m does not exist i.e. line parallel to y-axis
(iii) Slope of line joining two points A(x1, y1) & B(x2, y2) is
(iv) If a line equally inclined with co-ordinate axes then slope is ± 1.
(6) Intercepts : The point where a line cuts the x-axis (or y-axis) is called its x-intercept (or y-intercept).
(i) Intercepts may be +ve, -ve or zero.
(ii) A line making an intercept of -a with y-axis means the line passing through (0,-a)
(iii) A line makes equal non-zero intercept with both co-ordinate axes then slope is -1.
(iv) A line makes non-zero intercept with both co-ordinate axes equal in magnitude then slope is ±1.
================================================
Point Slope Form and Two Point Form - Straight Lines, Class 11, Maths
C. standard equations of straight lines
(1) General Form : Any first degree equation of the form Ax + By + C = 0, where A, B, C are constant always represents general equation of a straight line (at least one out of A and B is non zero.)
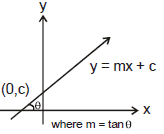
(2) Slope - Intercept Form :
y = mx + c
where m = slope of the line = tanθ
c = y intercept
(3) Intercept Form :
x intercept = a
y intercept = b
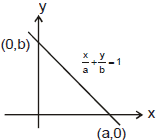
(4) Normal Form :
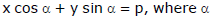 , where α is the angle which the perpendicular to the line makes with the axis of x and ρ is the length of the perpendicular from the origin to the line. p is always positive
, where α is the angle which the perpendicular to the line makes with the axis of x and ρ is the length of the perpendicular from the origin to the line. p is always positive

(5) Slope Point Form :
Equation : y - y1 = m (x - x1), is the equation of line passing through the point (x1, y1) and having the slope 'm'
(6) Two points Form :
Equation : y - y1 = , is the equation of line passing through two points (x1, y1) and (x2, y2)
(7) Parametric Form :
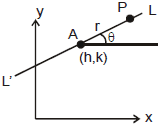
To find the equation of a straight line which passes through a given point A(h, k) and makes a given angle θ with the positive direction of the x-axis. P(x, y) is any point on the line LAL'.
Let AP = r, x - h = r cosθ, y - k = r sinθ
is the equation of the straight line LAL'.
Any point on the line will be of the form (h + r cosθ, k + r sinθ), where |r| gives the distance of the point P from the fixed point (h, k)
Note : If point P is taken relatively upward to A then r is positive otherwise negative. If line is parallel to x-axis then for he point right to A, r is positive and for left to A, r is negative.
D. REDUCTION OF GENERAL EQUATION TO DIFFERENT STANDARD FORMS
(1) Slope - Intercept Form :
To reduce the equation Ax + By + C = 0 to the form y = mx + c
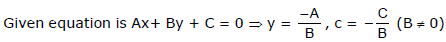
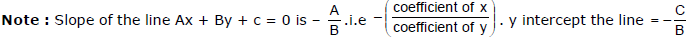
(2) Intercept Form :
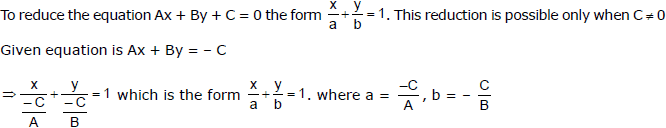
Note : Intercept on the x-axis = , intercept on the y-axis =
. Thus intercept of a straight line on the x-axis can be obtained by putting y = 0 in the equation of the line and then finding the value of x. similarly, intercept on the y-axis can be obtained by putting x = 0 and solving for y.
(3) Normal form :
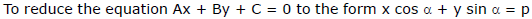
Given equation is Ax + By + C = 0 or, Ax + By = - C

Note : In the normal form 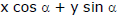 = p, p is always taken as positive.
= p, p is always taken as positive.
Ex.5 Reduce the line 2x - 3y + 5 = 0, in slope intercept, intercept and normal forms.
Sol.
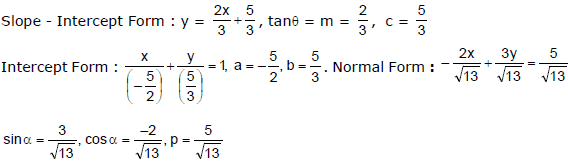
Ex.6 Find the equations of the lines which pass through the point (3, 4) and the sum of their respective intercepts on the axes is 14.
Sol.
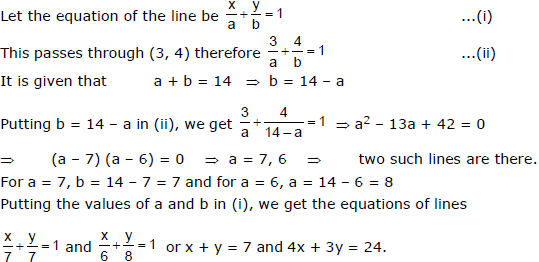
Ex.7 A rod of steel is fixed at A (4, 0) and a toy is placed on it at B (0, 4). Now rod is rotated about A through an angle of 15° in clockwise direction, then find the new position of a toy.
Sol.
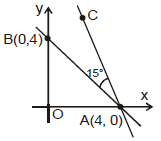
Let new position of a toy be C.
Slope of AB = ⇒ θ = 135°
Rod is rotated through 15° in clockwise
θnew = 135° - 15° = 120°
AB = ⇒ h = 4, k = 0
Hence C = (h + r cosθ, k = r sinθ) = (4 + 4 cos 120°, 0 +
sin 120°) =
Ex.8 If the straight line through the point P(3, 4) makes an angle π/6 with the x-axis and meets the line
12x + 5y + 10 = 0 at Q, find the length of PQ.
Sol. The equation of a line passing through P(3, 4) and making an angle = π/6 with the x-axis is
 where r represents the distance of any point on this line from the given point
where r represents the distance of any point on this line from the given point
P(3, 4). The co-ordinates of any point Q on this line are
If Q lies on 12x +15y + 10 = 0, then
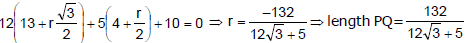
Ex.9 A canal is kms from a place and the shortest route from this place to the cenal is exactly north-east. A village is 3 kms north and 4 kms east from the place. Does it lie on canal?
Sol. Let AB be the canal and O be the given place.
Let L be the foot of perpendicular from O to AB.
Given, OL = 9/2. And 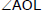 = 45°
= 45°
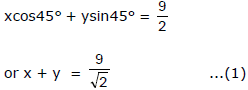
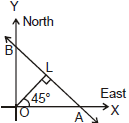
Let S be the given village, then S = (4, 3). Putting x = 4 and y = 3 in equation (1), we get 4 + 3 = , which is not true. Thus the co-ordinates of S doesn't satisfy equation (1) and hence the given village does not lie on the canal.
(4) Position of a point w.r. to a line L : Ax + By + c = 0
(i) If the points P(x1, y1) & Q(x2, y2) lies on the same side of the line Ax + By + C = 0 then the expressions Ax1 + By1 + C & Ax2 + By2 + C have same sign otherwise if P and Q lies on opposite side then Ax1 + By1 + C and Ax2 + By2 + C will have opposite sign.
(ii) If only one point is given then position of that point is checked w.r. to origin.
Ex.10 Find the range of q in the interval (0, π) such that the points (3, 5) and (sinθ, cosθ) lie on the same side of the line x + y - 1 = 0
Sol.
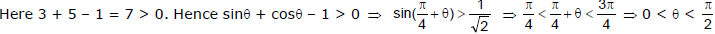
=================================================
Angle Between Two lines - Straight Lines, Class 11, Maths
E. ANGLE BETWEEN TWO STRAIGHT LINES

Notes :
(i) If the two lines are perpendicular to each other then m1m2 = -1
(ii) Any line perpendicular to ax + by + c = 0 is of the form bx - ay + k = 0
(iii) If the two lines are parallel or coincident, then m1= m2
(iv) Any line parallel to ax + by + c = 0 is of the form ax + by + k = 0
(v) If any of the two lines is perpendicular to x-axis, then the slope of that line is infinite.
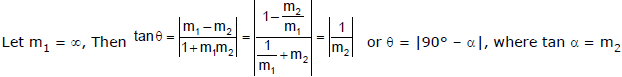
i.e. angle θ is the complimentary to the angle which the oblique line makes with the x-axis.
(vi) If lines are equally inclined to the coordinate axis then m1 + m2 = 0
Ex.11 Find the equation to the straight line which is perpendicular bisector of the line segment AB, where A, B are (a,b) and (a', b') respectively.
Sol. Equation of AB is y - b = i.e. y (a' - a) - x (b' - b) = a'b - ab'.
Equation to the line perpendicular to AB is of the form (b' - b)y + (a' - a)x + k = 0 ....(1)
Since the midpoint of AB lies on (1),
Hence the required equation of the straight line is
(1) Equation of straight Lines passing through a given point and equally inclined to a given line :
Let the straight passing through the point (x1, y1) and make equal angles with the given straight line y = mx + c. If m is the slope of the required line and a is the angle which this line makes with the given line then
(2) The above expression for tana, given two values of m, say mA and mB.
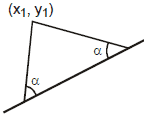
The required equations of the lines through the point (x1, y1) and making equal angles a with the given line are
y - y1 = mA(x - x1), y - y1 = mB (x - x1)
Ex.12 Find the equation to the sides of an isosceles right-angled triangled, the equation of whose hypotenuse is 3x + 4y = 4 and the opposite vertex is the point (2, 2).
Sol. The problem can be restarted as :
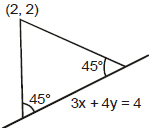
Find the equation to the straight lines passing through the given point (2, 2) and making equal angles of 45° with the given straight line 3x + 4y - 4 = 0. Slope of the line 3x + 4y - 4 = 0 is 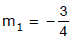
⇒ , i.e.,
mA = , and mB = - 7
Hence the required equations of the two lines are
y - 2 = mA(x - 2) and y - 2 = mB (x - 2) ⇒ 7y - x - 12 = 0 and 7x + y = 16.
=================================================================
Distance of a Point from a Line and Distance between 2 Parallel Lines - Straight Lines, Class 11, Maths
F. DISTANCE BETWEEN POINT & LINE AND TWO PARALLEL LINES
(1) Length of the Perpendicular from a Point on a Line :
The length of the perpendicular from P(x1, y1) on ax + by + c = 0 is
The length of the perpendicular from origin on ax + by + c = 0 is
(2) The distance between two parallel lines :
The distance between two parallel lines : ax + by + c1 = 0 and ax + by + c2 = 0 is
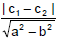
(3) Area of parallelogram with given sides :
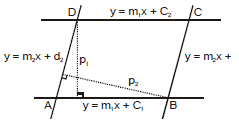
(4) Condition of parallelogram as shown becomes a rhombus :
(5) Reflection (Image) of a point P(a, b) about a line (ax + by + c = 0)
(6) Foot of perpendicular from a point 
(7) Shifting of the origin :
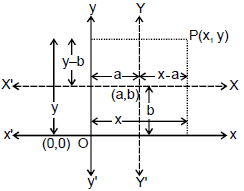
x, y ⇒ old co-ordinates axes
X, Y ⇒ New co-ordinate axes
X = 0 ⇒ x - a = 0 ⇒ x = a
Y = 0 ⇒ y - b = 0 ⇒ y = b
Slope and area of closed figure remains unchanged under the translation of co-ordinate axes.
Ex.13 Three lines x + 2y + 3 = 0, x + 2y - 7 = 0 and 2x - y - 4 = 0 form 3 sides of two squares. Find the equation of remaining sides of these squares.
Sol.
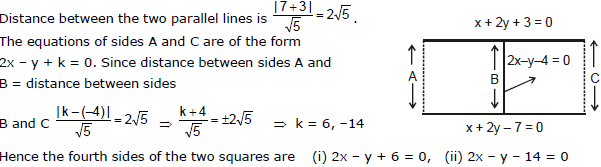
Ex.14 Find the foot of the perpendicular drawn from the point (2, 3) to the line 3x - 4y + 5 = 0. Also, find the image of (2, 3) in the given line.
Sol.
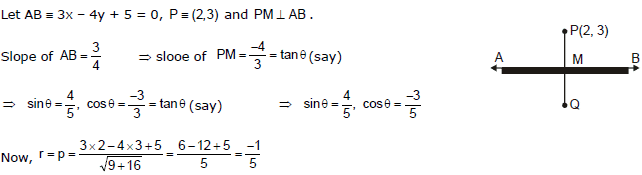 Which is the foot of the perpendicular.
Which is the foot of the perpendicular.
Let Q be the image of P
G. BISECTORS OF THE ANGLES BETWEEN TWO GIVEN LINES
Angular bisector is the locus of a point which moves in such a way so that its distance from two intersecting lines remains same.
The equation of the two bisectors of the angles between the lines a1x + b1y + c1 = 0 and
a2 x + b2y + c2 = 0 are .
If the two given lines are not perpendicular i.e. a1 a2 + b1 b2 ¹ 0, then one of these equation is the equation of the bisector of the acute angle and the other that of the obtuse angle.
Note : Whether both lines are perpendicular or not but the angular bisectors of these lines will always be mutually perpendicular.
(1) The bisectors of the acute and the obtuse angles :
Take one of the lines angle let its slope be m1 and take one of the bisectors and let its slope be m2. If q be the acute angle between them, then find .
If then the bisector taken is the bisector of the obtuse angle and the other one will be the bisector of the acute angle. If
then the bisector taken is the bisector of the acute angle and the other one will be the bisector of the obtuse angle.

(2) The equation of the bisector of the angle containing the origin
Write the equations of the two lines so that the constants c1 and c2 become positive. Then the equation is the equation of the bisector containing the origin.
Notes :
(i) If , then the origin will lie in the acute angle and if
, then origin will lie in the obtuse angle.
(ii) The note (i) is helpful in finding the equation of bisector of the obtuse angle or acute angle directly.
(3) The equation of the bisector of the angle which contains a given point
The equation of the bisector of the angle between the two lines containing the point is
or
according as
and
are of the same sings or of opposite signs.
Ex.15 For the straight line and
, find the equation of the
(i) bisector of the obtuse angle between them.
(ii) bisector of the actus angle between them.
(iii) bisector of the angle which contains (1, 2).
Sol. Equations of bisectors of the angles between the given lines are
and
.
 is the acute angle between the line
is the acute angle between the line and the bisector
, then
Hence
(i) The bisector of the obtuse angle is
(ii) The bisector of the acute angle is
(iii) The bisector of the angle containing the origin
(i) For the point 
Hence equation of the bisector of the angle containing the point (1, 2) is
Alternative : 5 lines. Similarly bisector of obtuse angle is 9x - 7y - 41 = 0.
(4) The equation of reflected ray :
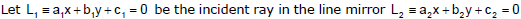
Let L3 be the reflected ray from the line L2. Clearly L2 will be one of the bisectors of the angles between L1 and L3. Since L3 passes through A, 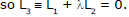
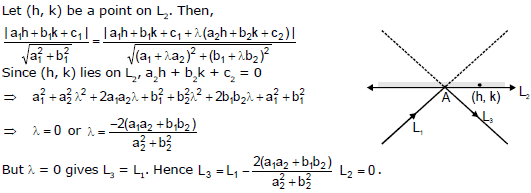
Note : Some times the reflected ray L3 is also called the mirror image of L1 in L2.
==============================================
Family of Lines - Straight Lines, Class 11, Maths
H. Family of Lines
The general equation of the family of lines through the point of intersection of two given lines is
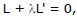 where L = 0 and L' = 0 are the two given lines, and
where L = 0 and L' = 0 are the two given lines, and 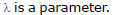 Conversely, any line of the form
Conversely, any line of the form 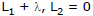 passes through a fixed point which is the point of intersection of the lines
passes through a fixed point which is the point of intersection of the lines
L1 = 0 and L2 = 0.
The family of lines perpendicular to a given line ax + by + c = 0 is given by bx - ay + k = 0, where k is a parameter.
The family of lines parallel to a given line ax + by + c = 0 is given by ax + by + k = 0, where k is a parameter.
Ex.16 Show that all the chords of the curve 3x2 - y2 - 2x + 4y = 0, which subtend a right angle at the origin pass through a fixed point. Find that the point.
Sol. Let the equation of chord be lx + my = 1. So equation of pair of straight line joining origin to the points of intersection of chord and curve.

(1) One Parameter Family of Straight Lines
If a linear expression L1 contains an unknown coefficient, then the line L1 = 0 can not be a fixed line. Rather it represents a family of straight lines known as one parameter family of straight lines. e.g. family of lines parallel to the x-axis i.e. y = c and family of straight lines passing through the origin i.e. y = mx.
Each member of the family passes a fixed point. We have two methods to find the fixed point.
Method (i) :
Let the family of straight lines of the form ax + by + c = 0 where a, b, c are variable parameters satisfying the condition al + bm + cn = 0, where I, m, n, are given and n ¹ 0. Rewriting the condition as a 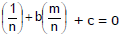 and comparing with the given family of straight lines, we find that each member of it passes through the fixed point
and comparing with the given family of straight lines, we find that each member of it passes through the fixed point
Ex.17 If the algebraic sum of perpendiculars from n given points on a variable straight line is zero then prove that the variable straight line passes through a fixed point.
Sol. Let n given points be (x1, y1) where i = 1, 2 .......... n and the variable line is ax + by + c = 0, Given that 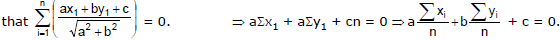
Hence the variable straight line always passes through the fixed point .
Method (ii) :
If a family of straight lines can be written as 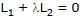 where L1, L2 are two fixed lines and
where L1, L2 are two fixed lines and 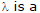 parameter, then each member of it will pass through a fixed point given by point of intersection of L1 = 0 and L2 = 0.
parameter, then each member of it will pass through a fixed point given by point of intersection of L1 = 0 and L2 = 0.
Note : If L1= 0 an L2 = 0 are parallel lines, they will meet at infinity.
Ex.18 Prove that each member of the family of straight lines
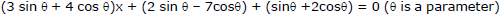
passes through a fixed point.
Sol. The given family of straight lines can be rewritten as (3x + 2y + 1) sinθ +(4x - 7y + 2) cosθ = 0
or, (4x - 7y + 2) + tanθ (3x + 2y + 1) = 0 which is of the form 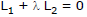
Hence each member of it will pass through a fixed point which is the intersection of 4x - 7y + 2 = 0 and
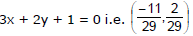
(2) Concurrency of Straight Lines : The condition for 3 lines a1x + b1y + c1 = 0, a2x + b2 + c2 = 0, a3x + b3x + b3y + c3 = 0 to be concurrent is
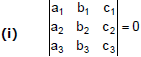
(ii) There exist 3 constants l, m, n (not all zero at the same time) such that L1 + mL2 + nL3 = 0, where L1 = 0, L2 = 0 and L3 = 0 are the three given straight lines.
(iii) the three lines are concurrent if any one of the lines passes through the pint of intersection of the other two lines.
I. Pair of Straight lines
The combined equation of pair of straight lines L1 = a1x + b1y + c1 = 0 and L2 = a2x + b2y + c2 = 0 is (a1x + b1y + c1) (a2x + b2y + c2) = 0 i.e. L1L2 = 0. Opening the brackets and comparing the terms with the terms of general equation of 2nd degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we can get all the following results for a pair of straight lines.
The general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of straight 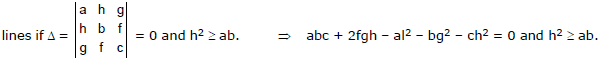
The homogeneous second degree equation ax2 + 2hxy + by2 = 0 represents a pair of straight lines through the origin if 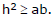
If the lines through the origin whose joint equation is ax2 + 2hxy + by2 = 0, are y = m1x and
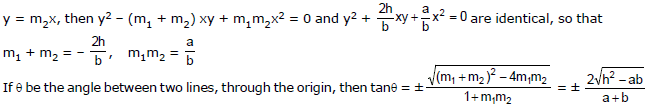
The lines are perpendicular if a + b = 0 and coincident if h2 = ab.
In the more general case, the lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 will be perpendicular if a + b = 0, parallel if the terms of second degree make a perfect square i.e. ax2 + 2hxy + by2 gets converted into (l1x + 2hxy + by2 gets converted into (l1x ± m1y)2, coincident if the whole equation makes a perfect square i.e. ax2 + 2hxy + by2 + 2fy + c can be written as (lx + my + n)2.
Note : Point of intersection of the two lines represented by ax2 + 2hxy + by2 + 2gx + 2fy +c = 0 is 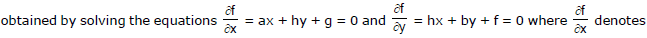
the derivative of f with respect to y, keeping x constant. The fact can be used in splitting ax2 + by2 + 2hxy + 2gx + 2fy + c = 0 into equations of two straight lines. With the above method, the point of intersection can be found. Now only the slopes need to be determined.
If should be noted that the line ax + hy + g = 0 and hx + by + f = 0 are not the lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0. These are the lines concurrent with the lines represented by given equation.
(Homogenization) Joint equation of pair of lines joining the origin and the points of intersection of a curve and a line :
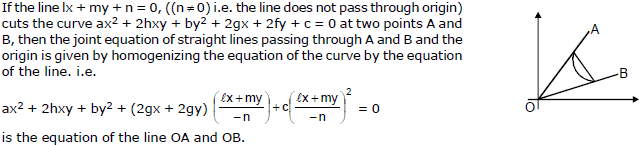
Ex.19 If the lines ax + y + 1 = 0, x + by + 1 = 0 and x + y + c = 0(a, b and c being distinct and different from 1) are concurrent, then prove that = 1.
Sol.
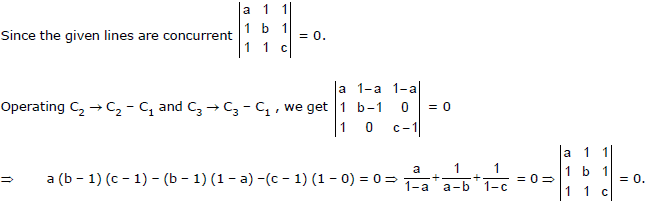
Ex.20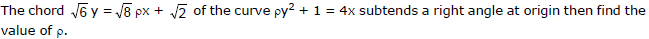
Sol.
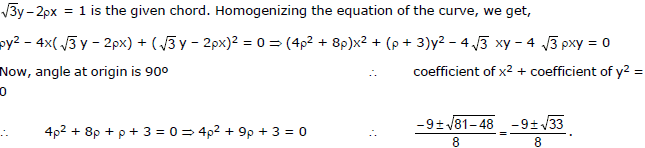
FAQs on Straight Lines Class 11 Notes, Maths (IIT)
| 1. What are straight lines in mathematics? |  |
| 2. What are the equations of a straight line? |  |
| 3. How to find the slope of a straight line? |  |
| 4. What is the importance of straight lines in real life? |  |
| 5. What are the applications of straight lines in mathematics? |  |















