Permutation & Combination
(A) Fundamental Principle of counting :
If an event can occur in `m' different ways, following which another event can occur in `n' different ways, then total number of ways of simultaneous occurrence of both events in definite order is = m × n (can be extended to any no. of events)
(B) What's Permutation & Combination ?
(1) Permutation : * Arrangement of things taken some or all at a time.
* Order of occurrence of events is important.
(2) Combination : * Collection or selection of things taken some or all at a time.
* Order of occurrence of events in not important
Note : All GOD made things in general are treated to be different and all man made things are to be spelled whether like or different
(C) Factorial :
(1) n ! =  = product of 1st `n' natural numbers ⇒ n ! = 1 × 2 × .......... × n
= product of 1st `n' natural numbers ⇒ n ! = 1 × 2 × .......... × n
(2) (n - 1)! =  ⇒
⇒ 
(3) factorial of negative numbers is not defined.
(D) Useful Theorems :
T-1 : Number of permutations of `n' distinct things taken r' at a time 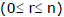
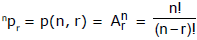
T-2 : Numbers of combinations/selections of `n' distinct things taken `r' at a time 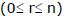
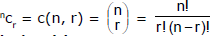
Note :- Derived Identities :
(1) ncr + ncr - 1 = n + 1cr
(2) ncr = ncn - r
(3) if ncx = ncy ⇒ x = y or x + y = 0
(4) npr = r ! . ncr
(5) (2n)! = 2n.n! {1.3.5........(2n - 1)}
(E) Formation of Groups :
(1) Number of ways of dividing (m + n) different things in two groups having `m' and `n' things are :  ;
;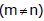
(i) If m = n, then number of groups = 
(ii) If `2n' things are to be equally distributed among 2 persons then, no. of ways =  × 2!
× 2!
(2) IIIy by (m + n + p) different things can be divided into 3 unequal groups is 
(i) If all groups are equal then number of ways = 
(ii) If `3n' things are to be equally distributed among 3 persons then, number of ways= 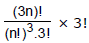
Note :- This can be extended to any number of groups.
(F) Permutation of alike objects :
Number of permutation of `n' things taken all at a time out of which
(1) `p' are similar and of one kind
(2) `q' are similar and of second kind
(3) and rest `r' are all different = 
Note :- Be careful if you encounter the following language used in problems
→ Number of other ways
→ Number of ways of rearranging
→ If as many more words as possible
(G) Circular permutation :
(1) Number of circular permutations of `n' different things taken `r' at a time = ncr (r - 1)!
(2) If clockwise & Anti-clockwise arrangements are considered as same then, ncr 
(3) Number of circular permutations of `n' things out of which `p' are alike and rest are different = 
(H) Total number of combinations :
(1) Number of ways of selecting at least one thing out of `n' different things is
= nc1 + nc2 +.............+ ncn = 2n - 1
(2) Number of ways of selecting at least one thing out of (p + q + r +..........) things in which p are alike of one kind, q of second kind & so on is = (p + 1) (q + 1) (r + 1) ........... -1
(I) Number of ways in which N can be resolved as a product of 2 divisors :
(1) N = pa . qb ...........p & q are prime
= 
(2) Number of ways in which `N' can be resolved as a product of 2 divisors which are relatively prime = 2n-1 , where n → number of primes involved in prime factorization of N.
(J) Maximizing ncr :
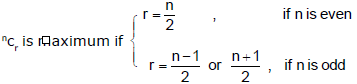
(K) Dearrangement :
Number of ways in which `n' letters can be placed in `n' directed envelopes so that no letter goes into its own envelope is = n!
(L) Distribution of alike objects :
(1) Number of ways of distributing `n' identical things to `p' persons where each person can receive one, none or more things is = n + p - 1Cp - 1
(2) Number of ways of distributing `n' identical things to `p' persons where each person should receive at least one object is = n - 1Cp - 1
(M) Grid Problem :
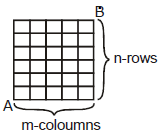
Number of ways of reaching B,
starting from point A are =  .
.
FAQs on Permutations and Combinations, Chapter Notes, Class 11, Maths - JEE
| 1. What is the difference between permutation and combination? |  |
| 2. How do we calculate permutations and combinations? |  |
| 3. What are the real-life applications of permutations and combinations? |  |
| 4. What is the difference between a permutation and a combination with repetition? |  |
| 5. What is the difference between a permutation and a combination with replacement? |  |

|
Explore Courses for JEE exam
|

|


















