Increasing and Decreasing Functions & Monotonicity | Mathematics (Maths) for JEE Main & Advanced PDF Download
Increasing and Decreasing Functions
A function is basically a relation between input and output such that, each input is related to exactly one output.Functions can increase, decrease or can remain constant for intervals throughout their entire domain. Functions are continuous and differentiable in the given intervals.
An interval in Maths is defined as a continuous/connected portion on the real line. Since it is a “portion of a line”, it basically is a line segment which has two endpoints. So, an interval has two endpoints. Easy to keep track, let’s name our interval and the endpoints and in an interval, assume any two points viz.
x1 and x2 such that x1 < x2. Now, there can be a total of four different cases:
- If f(x1) ≤ f(x2), the function is said to be non-decreasing in l
- If f(x1) ≥ f(x2), the function is said to be non-increasing in l
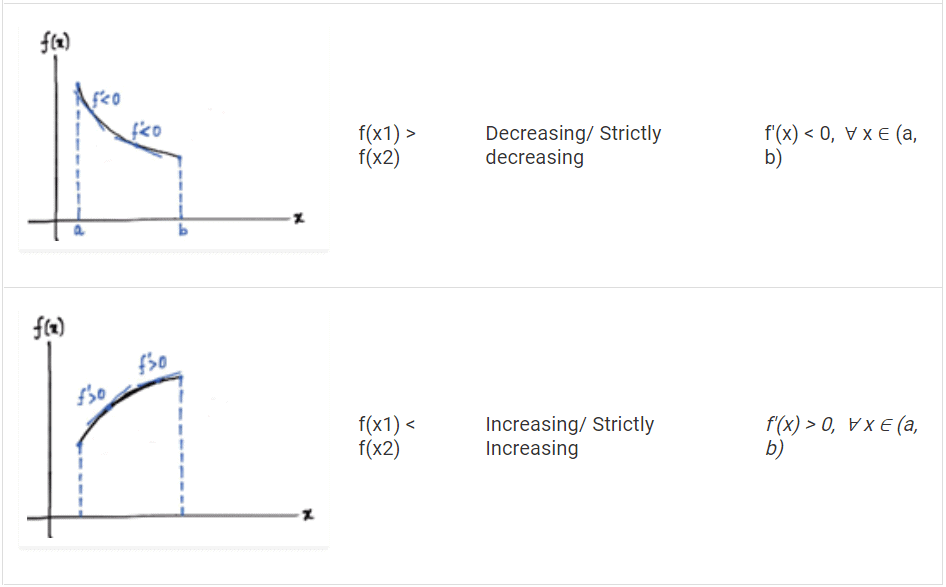
- If f(x1) > f(x2), the function is said to be decreasing (strictly) in l
- If f(x1) < f(x2), the function is said to be increasing (strictly) in l
This increasing or decreasing behaviour of functions is commonly referred to as monotonicity of the function. A monotonic function is defined as any function which follows one of the four cases mentioned above. Monotonic basically has two terms in it. Mono means one and tonic means tone. Together, it means, “in one tone”. When we tell that a function is non-decreasing, does it mean that it is increasing? No. It can also mean the function not varying at all! In other words, function having a constant value for some interval. Never confuse non-decreasing with increasing. That was the definition of increasing and decreasing functions. Let us now see how to know where and in which way the function is behaving.
Test for increasing and decreasing functions
Let us now use derivative of a function to determine the behaviour of a function. To test the monotonicity of a function f, we first calculate it’s derivative f′. There is a small catch here. Before starting the test, make sure that is continuous in the interval [a, b] and differentiable in (a, b). So, for all of the four cases discussed in previous heading, we have tests as:
- For function to be non-decreasing in l, f′(x) ≥ 0,∀ x∈(a, b)
- For function to be non-increasing in l, f′(x) ≤ 0,∀ x∈(a, b)
- For function to be decreasing/strictly decreasing in l, f′(x)< 0,∀ x∈(a, b)
- For function to be increasing/strictly increasing in l,f′(x) > 0,∀ x∈(a, b)<
Let us see examples of each case.

That was increasing and decreasing functions, monotonic functions and monotonicity explained. This concept is particularly very useful for drawing graphs of functions.
A. Definitions
The function f(x) is called strictly increasing on the open interval (a, b) if for any two points x1 and x2 belonging to the indicated interval and satisfying the inequality x1 < x2 the inequality f(x1) < f(x2) holds true.
The function f(x) is called strictly decreasing on the open interval (a, b) if for any points x1 and x2 belonging to the indicated interval and satisfying the inequality x1 < x2 the inequality f(x1) > f(x2) holds true.
A function f is said to be non-decreasing in an interval I contained in the domain of f
If for all numbers x1, x2 in I.
If f(x1) < f(x2) whenever x1 < x2 for all numbers x1, x2 in I,
then f is said to be strictly increasing in the interval I. Non-increasing and strictly decreasing functions are defined in a similar way. If f is strictly increasing in I, then the graph of f is rising as we traverse it from left to right; if f is strictly decreasing in I, the graph of f is falling in I. Some examples are show in Figure.
If a function f is either non-decreasing in an interval I or non-increasing in I, then f is said to be monotonic in I. Similarly, f is said to be strictly monotonic in I if f is either strictly increasing in I or strictly decreasing in I.
Basic definition test :
The function f(x) is said to be strictly increasing at a point x0 if for a sufficiently small h > 0 the condition (Fig. 1) f(x0 - h) < f(x0) < f(x0 + h) is fulfilled.
The function f(x) is said to be strictly decreasing at a point x0 if for a sufficiently small h > 0 the condition (Fig. 2) f(x0 - h) > f(x0) > f(x0 + h) is fulfilled.
A differentiable function is called increasing in an interval (a, b) if it is increasing at every point within the interval (but not necessarily at the end points). A function decreasing in an interval (a, b) is similarly defined.
Sufficiency Test :
If the derivative function f '(x) in an interval (a , b) is every where positive, then the function f (x) in this interval is Increasing ; If f '(x) is every where negative, then f (x) is Decreasing.
Note : The test (criterion) also holds true when the derivative takes on zero values in the interval (a, b) so long as f (x) does not identically become zero throughout the interval (a, b) or in some interval (a', b') comprising a part of (a, b). The function f (x) would be a constant on such an interval.
If f'(a) = 0 then examine the sign of f'(a+) and f'(a-)
(a) If f'(a+) > 0 and f'(a-) > 0 then strictly increasing
(b) If f'(a+) < 0 and f'(a-) < 0 then strictly decreasing
Note : If a function is invertible it has to be either increasing or decreasing.
If a function is continuous in the intervals in which it rises and falls may be separated by points at which its derivative is zero or it fails to exist.
B. Critical Point
A critical point of a function f is a number c in the domain of f such the either f'(c) = 0 or f'(c) does not exist.
Ex.1 Find the critical points of f(x) = x3/5 (4 - x).
Sol.
Therefore, f'(x) = 0 if 12 – 8x = 0, that is, x = 3/2. and f'(x) does not exist when x = 0.
Thus, the critical points are 3/2 and 0.
Ex.2 Find the critical numbers for the function
Sol.
The derivative is not defined at x = 2, but f is not defined at 2 either, so x = 2 is not a critical number. The actual critical numbers are found by solving f'(x) = 0 :
= 0
x = 3 This is the only critical number since ex > 0.
Ex.3 Find all possible values of the parameter ' b ' for which the function,
f (x) = sin 2 x - 8 (b + 2) cos x - (4 b2 + 16 b + 6) x
is monotonic decreasing throughout the number line and has no critical points.
Sol. f ' (x) = 2 cos 2 x + 8 (b + 2) sin x - (4 b2 + 16 b + 6)
= 2 (1 - 2 sin2 x) + 8 (b + 2) sin x - (4 b2 + 16 b + 6)
= - 4 [ sin2 x - 2 (b + 2) sin x + (b2 + 4 b + 1) ]
for monotonic decreasing and no critical points
Now, D = 4 (b + 2)2 - 4 (b2 + 4 b + 1) = 4 [3] = 12 which is always positive .
Now let sin x = y ; y ε [- 1 , 1]
g (y) = y2 - 2 (b + 2) y + (b2 + 4 b + 1)
we have to find those values of ' b ' for which g (y) > 0 for all y ε (- 1 , 1)
Conditions are
First condition gives 1 + 2 (b + 2) + b2 + 4 b + 1 > 0
b2 + 6 b + 6 > 0 .....(1) & < -1 or b < - 3 .....(2)
Ex.4 If where 0 < x < 1, then
Sol. Put x = π/6 & π/3 and observe the behavior of f(x) & g(x) . Alternatively
consider = 2 (1 - cos x) - x sin x
consider x - 2 sin x + x cos x
= 2x cos2x - 4 sin x cos x
Ex.5 Find possible values of a such that f(x) = e2x - (a + 1) ex + 2x is strictly increasing for x ε R.
Sol. f(x) = e2x - (a + 1) ex + 2x
f '(x) = 2e2x - (a + 1) ex + 2
Now, f(x) = e2x - (a + 1) ex + 2x ≥ 0 for x ∈R
Aliter : 2e2x – (a + 1) ex + 2 ≥ 0 for x ∈R
putting ex = t ; t ∈ (0,∝)
2t2 – (a + 1) t + 2 ≥ 0 for t∈ (0, ∝)
Hence either
(i) D ≤ 3 ⇒ (a + 1)2 – 4 ≤ 0 ⇒ (a + 5) (a – 3) ≤ 0 ⇒ a ∈ [–5, 3]
(ii) both roots are negative
D ≥ 0 & -b/2a < 0 & f(0) ≥ 0
Taking union of (i) and (ii), we get a ∈ (–∝, 3].
Ex. 6 Prove that the function f(x) = is strictly decreasing in (e, ∞). Hence, Prove that 303202 < 202303.
Sol.
We have f(x) = ,x > 0,
⇒ f(x) strictly decreases in (e,∝) Thus, we have f(303) < f(202)
i.e . 202 ln (303) < 303 ln (202)
⇒ 303202 < 202303 which is the desired result.
Ex.7 Let f(x) = x3 + 2x2 + x + 5. Show that f(x) has only one real root a such that [α] = -3.
Sol. We have f(x) = x3 + 2x2 + x + 5, x ∈ R and f '(x) = 3x2 + 4x + 1 = (x + 1) (3x + 1), x ∈ R
Drawing the number line for f'(x), we have f(x) strictly increases in (–∝, –1) strictly decreases in (–1, –1/3) strictly increases in (–1/3, ∝)
Also, we have f(–1) = –1 + 2 – 1 + 5 = 5 and
The graph of f(x) (see fig.) shows that f(x) cuts the X-axis only once.
Now, we havef(–3) = – 27 + 12 – 3 + 5 = – 13 and f(–2) = –8 + 8 – 2 + 5 = 3.
Which are of opposite signs. This proves that the curve cuts the X-axis somewhere between –2 and –3.
⇒ f(x) = 0 has a root α lying between – 2 and –3. Hence [α] = –3
Ex.8 Find the number of real roots of the equation = c where b1 < b2 < ..... <bn.
Sol.
Consider the function f(x) =
= f(x) strictly decreases in (–α, b1) U (b1,b2) U ... U (bn – 1, bn)
Now, we have
The plot of the curve y = f(x) is shown alongside.
Ex.9 If f : R → R and f is a polynomial with f(x) = 0 has real and distinct roots, show that the equation, [ f ' (x) ]2 - f(x) . f '' (x) = 0 cannot have real roots.
Sol. Let f(x) = c (x - x1) (x - x2) ...... (x - xn)
Again Let
⇒ h ' (x) < 0 ⇒ f(x) . f '' (x) - [f ' (x)]2 < 0
Alternatively : a function f(x) satisfying the equation [f ' (x)]2 - f(x) . f '' (x) = 0 is which can't have any root.
C. Intervals of Monotonocity
Ex.10 Find the intervals of monotonocity of the following functions :
(a) f(x) =
(b) f(x) =
(c) f(x) =
Sol.
(a) We have
Now, from the sign scheme for f'(x), we have ⇒ f(x) strictly increases i (-∞, 0)
strictly decreases in (0, 1) ; strictly increases in (1, 2) ; strictly decreases in (2, ∞)
Ans. : Increases in (-∞, 0), (1, 2); Decreases in (0, 1), (2, ∞)
(b) We have f(x)=2x2 – ln |x| and f '(x) = 4x – 1/x =
Now, from the sign scheme for f'(x), we have ⇒ f(x) strictly decreases in (-∞, -1/2)
strictly increases in (-1/2, 0) ; strictly decreases in (0, 1/2) ; strictly increases in (-1/2, ∞)
Ans. :
(c)
⇒ f(x) strictly decreases in (-∞, -3) ; strictly increases in (-3, 3) ; strictly decreases in (3, ∞).
Ans : Increases in (-3, 3) ; Decreases in (-∞, -3), (3, ∞)
Ex.11 A function f (x) is given by the equation , x2 f ' (x) + 2 x f (x) - x + 1 = 0 (x 0). If f (1) = 0 , then find the intervals of monotonocity of f.
Sol.
wherey = f (x)
Ans. : I in (- ∝, 0) U (1, ∝) ; D in (0, 1)
D. Operations on Monotonous Functions
I. (a) Negative : If f is an increasing function then its negative i.e. h = –f is a decreasing function.
By derivative h'(x) = –f'(x), f'(x) > 0 ∴h'(x) < 0
⇒ h is a decreasing function
In short – (an increasing function) = a decreasing function i.e. –I = D Similarly –D = I
(b) Reciprocal : Reciprocal of an increasing function is a decreasing function
II.(a) Sum : If f is an increasing function and g is also an increasing function their h = f + g is an increasing function.
By derivative
h'(x) = f'(x) + g'(x) f & g are increasing function, ⇒ f '(x) & g'(x) are positive ⇒ f '(x) + g'(x) is positive ⇒ f(x) + g(x) increases
In short, An increasing function + An increasing function = An increasing function
i.e. (i) I + I = I (ii) I + D = can’t say (iii) D + D = D
(b) Difference : Monotonocity of the difference of two function can be predicted using I(a) and II(a)
I - I = I + (-I) = I + D = can't say
I - D = I + (-D) = I + I = increasing
D - I = D + (-I) = D + D = decreasing
D - D = D + (-D) = D + I = can't say
III. (a) Product : Consider h = f × g
Case I : Both the function involved in the product i.e. f & g are positive
If f & g both are increasing function then h = f × g is also an increasing function.
In short I × I = I, I × D = can't say, D × D = D.
Case II : If any of the function takes negative values then we can predict the monotonocity by using I(a) & case I of III(a). If a function f is increasing & takes negative values & another function g is decreasing & takes positive values.
then h(x) = f(x) × g(x) = (-f(x)) × g(x) = - = increasing
(b) Division : Monotonocity of division of two functions can be predicted by using I(b) & III(a).
= I × I = I (assuming that both the functions I & D take positive values).
IV. Composition :
(I) I (I)= I
(II) I(D) = D
(III) D (I) = D
(IV) D(D) = I
Let h(x) = D(D(x)) x increases ⇒ D(x) decreases ⇒ D(D(x)) increases
E. Inequalities
General Approach to prove Inequalities :
To prove f(x) ≥ g(x) for x ≥ a, we Assume h(x) = f(x) – g(x)
Find h'(x) = f'(x) – g'(x)
If h'(x) ≥ 0 Apply increasing function h on x ≥ a to get h(x) ≥ h(a).
If h(a) ≥ 0 then h(x) ≥ 0 for x ≥ a i.e. then given inequality is true.
If h'(x) ≤ 0 Apply decreasing function h on x ≥ a to get h(x) ≤ h(a).
If h(a) ≤ 0 then h(x) ≤ 0 for x ≥ a i.e. the given inequality is false
Note : If the sign of h'(x) is not obvious then to determine its sign assume g(x) = h'(x) & apply the above procedure on g(x).
Ex.12 Prove that, 2 x sec x + x > 3 tan x for 0 < x <  /2 .
/2 .
Sol. f(x) = 2x sec x + x - 3 tan x
f ' (x) = 2 sec x + 2x sec x tan x + 1 - 3 sec2x = sec2 x [2 cos x + 2x sin x + cos2x - 3]
Consider g(x) = 2 cos x + 2x sin x + cos2x - 3
g ' (x) = - 2 sin x + 2x cos x + 2 sin x - 2 sin x cos x = 2 cos x (x - sin x) > 0 for x ε (0, /2)
Ex.13 Prove that tan x > x + for all x ε
.
Sol.
...(1)
Clearly, f(x) is defined at all x ∈ (0, π/2).
Now, f'(x) = sec2x – 1 x– x2 ...(2)
f''(x) = 2 sec2 x . tan x – 2x...(3)
f'''(x) = 2 sec4x + 4 sec2 x. tan2 x – 2 = 2 (1 + tan2x)2 + 4 sec2x . tan2 x – 2
= 2tan4x + 4 tan2x + 4 sec2x . tan2x > 0 for all x ∈ (0, π/2)
⇒ f'''(x) > 0 in the interval (0, p/2) ⇒ f''(x) is monotonic increasing in (0, π/2)
f''(x) > f''(0) when x ∈ (0, π/2).
But from (3), f''(0) = 0. Thus, f''(x) > 0 for all x ∈ (0, π/2)
∴f'(x) is monotonic increasing in (0, π/2)
∴f'(x) > f'(0) when x ∈ (0, π/2)
But from (2), f'(0) = 1 – 1 – 0 = 0.
Thus, f'(x) > 0 for all x ∈ (0, p/2)
∴f(x) is monotonic increasing in (0, π/2)
∴f(x) > f(0) when x ∈ (0, π/2)
But from (1), f(0) = 0.
Thus, f(x) > 0 for all x ∈ (0, π/2)
∴
Ex.14 Show that
Sol.
or
or
Since, f(x) is increasing for, x ≥ 0 ⇒ f(x) ≥ f(0)
⇒
Ex.15 Examine which is greater sin x tan x or x2. Hence evaluate
Sol. Let f(x) = sin x . tan x - x2
f '(x) = cos x . tan x + sin x . sec2x - 2x = sin x + sin x sec2 x - 2x
⇒ f ''(x) = cos x + cos x sec2 x + 2 sec2 x sin x tan x - 2
⇒ f ''(x) = (cos x + sec x - 2) + 2 sec2 x sin x tan x
Now cos x + sec x – 2 = and 2 sec2 x tan x . sin x > 0 because
⇒ f''(x) > 0 ⇒ f'(x) is M.I.
Hence f'(x) > f'(0)
⇒ f'(x) > 0 ⇒ f(x) is M.I. ⇒ f(x) > 0 ⇒ sin x tan x – x2 > 0
Hence sin x tan x – x2
Ex.16 Prove :
Sol. Consider the function f(x) = cot (x/2) – 1 – cot x, x ∈ (0, p)
⇒ f(x) strictly decreases in (0, π/2) strictly increases in (π/2, π)
⇒ f(x) has least value at x = π/2 ⇒ f(x) ≥ f(π/2) = 0
which proves the desired result.
Ex.17 Prove that Hence, show that the function f(x)=
strictly increases in (0, ∞).
Sol.
Consider the fucntion g(x) =
⇒ g(x) strictly decreases in (0, ∝) ⇒
which gives the desired result
Now, we have f(x)
[using result (1)] ⇒ f(x) strictly increases in (0, ∝)
Ex.18 Prove that
Sol.
Let f(x) = sin x tan x – x2 ⇒ f'(x) = sin x sec2x + sin x – 2x
⇒ f''(x) = 2 sin x sec2 x tan x + cos x – 2 + sec x
= 2 sin x tan x sec2 x + (cos x + sec x – 2)
⇒ f'(x) is an increasing function.
⇒ f'(x) > f'(0) ⇒ sin x sec2 x + sin x – 2x > 0
⇒ f(x) is an increasing function ⇒ f(x) > f(0) sin x tan x – x2 > 0 ⇒ sin x tan x > x2
Ex.19 Prove that sin 1 > cos (sin 1). Also show that the equation sin (cos (sin x)) = cos (sin (cos x)) has only one solution in
Sol. sin 1 > cos (sin 1) if
...(1)
Hence (1) is true ⇒ sin 1 > cos (sin 1).
Now let f(x) = sin (cos (sin x)) – cos (sin (cos x))
and f(0) = sin 1 – cos (sin 1) > 0
Since f(0) is positive and f(x) = 0 has one solution in
Ex.20 Using calculus establish the inequality, (xb + yb)1/b < (xa + ya)1/a , where x > 0 , y > 0 and b>a>0.
Sol. (xb + yb)1/b < (xa + ya)1/a
or T P T (tb + 1)a/b < ta + 1
Let f (t) = (tb + 1)a/b - ta - 1
Hence f'(t) < 0 i.e. f (t) is decreasing function
So f (t) < f (0) but f (0) = 0 ⇒ (tb + 1)a/b < ta + 1 Hence proved
Ex.21 Prove that the function f(x) = 2x3 + 21x2 - 60x + 41 is strictly positive in the interval (-∞, 1).
Sol.
f(x) = –2x3 + 21x2 – 60x + 41
f'(x) = –6x2 + 42x – 60 = – 6(x2 – 7x + 10) = –6(x – 5) (x – 2)
x ∈ (2, 5) ⇒ f'(x) > 0, i.e., f(x) is m.i.
and x Ï (2, 5) ⇒ f'(x) < 0 i.e., f(x) is m.d. ∴ x ∈ (–∝, 1) ⇒ f(x) is m.d.
When x ∈ (–∝, 1), x < 1; so, f(x) > f(1).
But f(1) = –2 + 21 – 60 + 41 = 0.
∴ x ∈ (–∝, 1) ⇒ f(x) > f(1) = 0
∴ f(x) is strictly positive in the interval (–∝, 1).
F. Rolle's Theorem
Let f be a function that satisfies the following three hypotheses :
1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a, b).
3. f(a) = f(b)
Then there is a number c in (a, b) such that f'(c) = 0
Before given the proof let's take a look at the graphs of some typical functions that satisfy the three hypotheses. Figure 1 shows the graph of four such functions. In each case it appears that there is atleast one point (c, f(c)) on the graph where the tangent is horizontal and therefore f'(c) = 0. Thus, Rolle's Theorem is plausible.
Proof : There are three cases :
Case I : f(x) = k, a constant. Then f'(x) = 0, so the number c can taken to be any number in (a, b).
Case II : f(x) > f(a) for some x in (a, b) [as in Figure 1(b) or (c)]
By the Extreme Value Theorem (which we can apply by hypothesis 1), f has a maximum value somewhere in [a, b]. Since f(a) = f(b), it must attain this maximum value at a number c in the open interval (a, b). Then f has a local maximum at c and, by hypothesis 2, f is differentiable at c. Therefore, f'(c) = 0 by Fermat's Theorem.
Case III : f(x) < f(a) for some x in (a, b) [as in Figure 1(c) or (d)]
By the Extreme Value Theorem, f has minimum value in [a, b] and, since f(a) = f(b), it attains this minimum value at a number c in (a, b). Again f'(c) = 0 by Fermat's Theorem.
Ex.22 Prove that the equation x3 + x - 1 = 0 has exactly one real root.
Sol. First we use the Intermediate Value Theorem to show that a root exists. Let f(x) = x3 + x - 1. Then f(0) = -1 < 0 and f(1) = 1 > 0. Since f is a polynomial, it is continuous, so the Intermediate Value Theorem states that there is a number c between 0 and 1 such that f(c) = 0. Thus, the given equation has a root.
To show that the equation has no other real root, we use Rolle's Theorem and argue by contradiction. Suppose that it had two roots a and b. Then f(a) = 0 = f(b) and, since f is a polynomial, it is differentiable on (a, b) and continuous on [a, b]. Thus, by Rolle's Theorem, there is a number c between a and b such that f'(c) = 0. But for all x
(since x2 ≥ 0) so f'(x) can never be 0. This gives a contradiction. Therefore, the equation can't have two real roots.
Ex.23 Let f (x) & g (x) be differentiable for such that f (0) = 2, g (0) = 0, f (1) = 6 . Let there exist a real number c in [0, 1] such that f ' (c) = 2 g ' (c) , then the value of g (1)
Sol. Consider φ(x) = f (x) - 2 g (x) defined on [0, 1] since f (x) and g(x) are differentiable for therefore f (x) is differentiable on (0, 1) and continuous on [0, 1]
ø(0) = ø (0) - 2 g (0) = 2 - 0 = 2 ø (1) = f (1) - 2 g (1) = 6 - 2 g (1)
Now f '(x) = f '(x) - 2 g '(x) ⇒ f '(c) = f '(c) - 2 g '(x) = 0 (given)
⇒ f (x) satisfies Rolle's theorem on [0, 1] ∴ ø (0) =ø(1) ⇒ 2 - 6 - 2 g (1) ⇒ g (1) = 2
Our main use of Rolle's Theorem is in proving the following important theorem, which was first stated by another French mathematician, Joseph-Louis Lagrange.
Ex.24 If f(x) is continuous in [a, b] and differentiable in (a, b), prove that there is atleast one c ε(a, b), such that .
Sol. Let us consider a function, h(x) = f(x) - f(a) + A (x3 - a3)
Where A is obtained from the relation h(b) = 0.
So that, 0 = h(b) = f(b) - f(a) + A(b3 - a3) ...(i)
also, h(a) = 0
Since, (1) h(x) is continuous in [a, b] (2) h(x) is differentiable in (a, b) and (3) h(a) = 0 = h(b)
hence, all the three condition of Rolle's theorem. Then there must exists a'c' ε (a, b) such that f'(c) = 0.
⇒ f'(c) + A (3c2) = 0 or
G. The Mean Value Theorem
Let f be a function that satisfies the following hypotheses :
1. f is continuous on the closed interval [a, b].
2. f is differentiable on the open interval (a, b).
Then there is a number c in (a, b) such that
Before proving this theorem, we can see that it is reasonable by interpreting it geometrically. Figures (a) and (b) show that points A(a, f(a)) and B(b(b, f(b)) on the graphs of two differentiable functions. The slope of the secant line AB is
which is the same expression as on the roght side od eq. 1. Since f'(c) is the slope of the tangent line at the point (c, f(c)), the Mean Value Theorem, in the form given by Equation 1, says that there is at least one point P(c, f(c)) on the graph where the slope of the tangent line is the same as the slope of the secant line AB. In other words, there is a point P where the tangent line is parallel to the secant line AB.
Proof We apply Rolle’s Theorem to a new function h defined as the difference between f and the function whose graph is the secant line AB. Using Equation 3, we see that the equation of the line AB can be written as
First we must verify that h satisfies the three hypotheses of Rolle's Theorem.
1. The function h is continuous on [a, b] because it is the sum of f and a first-degree polynomial, both of which are continuous.
2. The function h is differentiable on (a, b) because both f and the first-degree polynomial are differentiable. In fact we can compute h' directly from Equation 4 :
(Note that f(a) and [f(b) - f(a)]/(b - a) are constants.)
3.
h(a) = f(a) – f(a) -
h(b) = f(b) – f(a) -
Since h satisfies the hypotheses of Rolle's Theorem, that theorem says there is a number c in (a, b) such that h'(c) = 0. Therefore
Ex.25 To illustrate the Mean Value Theorem with a specific function, let's consider f(x) = x3 - x, a= 0, b = 2. since f is a polynomial, it is continuous and differentiable for x, so it is certainly continuous on [0, 2] and differentiable on (0, 2) such that f(2) - f(0) = f'(c)(2 - 0)
Sol.
Ex.26 If for all x and f(0) = 0, show that 0.4 < f(2) < 2
Sol.
...(1)
f'(x) > 0 for all x [∴1 + x2 > 0]
Also given f(0) = 0 ...(2)
From (1), it follows that f(x) is differentiable at all x, therefore f(x) is also continuous at all x
∴ by Lagrange’s mean value theorem in [0, 2]
Now 0 < c < 2
...(4)
From (3), (4) and (5) it follows that 0.4 < f(2) < 2.
H. Curve Sketching
The following checklist is intended as a guide to sketching a curve y = f(x). Not every item is relevant to every function. (For instance, a given curve might not have an asymptote or possess symmetry.) But the guidelines provide all the information you need to make a sketch that displays the most important aspects of the function.
I. Domain It's often useful to start by determining the domain D of f, that is, the set of values of x for which f(x) is defined.
II. Intercepts The y-intercept is f(0) and this tells us where the curve intersect the y-axis. To find the x-intercepts, we set y = 0 and solve for x. (You can omit this step if the equation is difficult to solve.)
III. Symmetry
(a) If f(-x) = f(x) for all x in D, that is, the equation of the curve is unchanged when x is replaced by -x, then f is an even function and the curve is symmetric about the y-axis. This means that out work is cut in half. If we know what the curve looks like for then we need only reflect about the y-axis to obtain the complete curve [see Figure (a)]. Here are some examples : y = x2, y = x4, y = |x|, and y = cos x.
(b) If f(-x) = -f(x) for all x in D, then f is an odd function and the curve is symmetric about the origin. Again we can obtain the complete curve if we know what it looks like for [Rotate 180º about the origin; see Figure (b).] Some simple examples of odd functions are y = x, y = x3, y = x5, and y = sin x.
Figure
(c) If f(x + p) = f(x) for all x in D, where p is positive constant, then f is called a periodic function and the smallest such number p is called the period. For instance, y = sin x has period 2 and y = tan x has period
. If we know what the graph looks like in an interval of length p, then we can use translation to sketch the entire graph (see Figure ).
IV. Asypmtotes
(a) Horizontal Asymptotes. If either f(x) = L or
f(x) = L, then the line y = L is a horizontal asymptote of the curve y = f(x). If it turns out that
f(x) = ∞ (or - ∞), then we do not have an asymptote to the right, but that is still useful information for sketching the curve.
(b) Vertical Asymptotes. The line x = a is a vertical asymptote if at least one of the following statements is true :
(For rational functions you can locate the vertical asymptotes by equating the denominator to 0 after canceling any common factors. But for other functions this method does not apply.) Furthermore, in sketching the curve it is very useful to know exactly which of the statements in (ii) is true. If f(a) is not defined but a is an endpoint of the domain of f, then you should compute or
f(x), whether or not this limit is infinite,
V. Interval of Increase / Decrease Use the I/D Test. Compute f'(x) and find the intervals on which f'(x) is positive (f is increasing) and the intervals on which f'(x) is negative (f is decreasing).
VI. Local Maximum and Minimum Value Find the critical numbers of f [the number c where f'(c) = 0 or f'(c) does not exist]. Then use the First Derivative Test. If f' changes from positive to negative at a critical number c, then f(c) is a local maximum. If f' changes from negative to positive at c, then f(c) is a local minimum. Although it is usually preferable to use the First Derivative Test, you can use the Second Derivative Test if c is a critical number such that f''(c) 0. Then f''(c) > 0 implies that f(c) is a local minimum, whereas f''(c) < 0 implies that f(c) is a local maximum.
VII. Concavity and Points of Inflection Compute f'(x) and use the Concavity Test. The curve is concave upward where f''(x) > 0 and concave downward where f''(x) < 0. Inflection points occur where the direction of concavity changes.
VIII. Sketch the Curve Using the information in items A - G, draw the graph. Sketch the asymptotes as dashed lines, Plot the intercepts, maximum and minimum points, and inflection points. Then make the curve pass through these points, rising and falling according to E, with concavity according to G, and approaching the asymptotes. If additional accuracy is desired near any point, you can compute the value of the derivative there. The tangent indicates the direction in which the curve proceeds.
Ex.27 Use the guidelines to sketch the curve y = .
Sol.
I. The domain is {x|x2 – 1 ≠ 0} = {x | x ≠ ± 1} = (– ∝ , – 1) U (–1, 1) U (1. ∝)
II. The x-and y-intercepts are both 0.
III. Since f(-x) = f(x), the function f is even. The curve is symmetric about the y-axis.
IV. Therefore, the line y = 2 is a horizontal asymptote.
Since the Denominator is 0 when x = ±1, we compute the following limits :
Therefore, the lines x = 1 and x = -1 are vertical asymptotes. This information about limits and asymptotes enables us to draw the preliminary sketch in Figure, showing the parts of the curve near the aymptotes.
V.
Since f'(x) > 0 when x < 0 (x ≠ -1) and f'(x) < 0 when x > 0 when x > 0 (x ≠ 1), f is increasing on (-∝, -1) and (-1, 0) and decreasing on (0, 1) and (1, ∝).
VI. The only critical number is x = 0. Since f' changes from positive to negative at 0, f(0) = 0 is local maximum by the First Derivative Test.
VII.
Since 12x2 + 4 > 0 for all x, we have
f''(x) > 0 ⇔ x2 – 1 > 0 ⇔ |x| > 1
VIII. Using the information in V – VI, we finish the sketch in Figure.
Ex.28 Sketch the graph of f(x) = .
Sol.
I. Domain = {x|x + 1 > 0} = {x|x > –1} = (–1, ∝)
II. The x- and y-intercepts are both 0.
III. Symmetry : None
IV. Since there is no horizontal asymptote. Since
and f(x) is always positive, we have
and so the line x = –1 is a vertical asymptote.
V.
We see that f'(x) = 0 when x = 0 (notice that - 4/3 is not in the domain of f), so the only critical number is 0. Since f'(x) < 0 when -1 < x < 0 and f'(x) > 0 when x> 0, f is decreasing on (-1, 0) and increasing on (0, ∝)
VI. Since f'(0) = 0and f' changes from negative to positive at 0, f(0) = 0 is a local (and absolute) minimum by the first derivative.
VII.
Note that the denominator is always positive. The numerator is the quadratic 3x2 + 8x + 8, which is always positive because its discriminant is b2 – 4ac = –32, which is negative, and the coefficient of x2 is positive. Thus, f''(x) > 0 for all x in the domain of f, which means that f is concave upward on (-1, to) and there is no point of inflection.
VIII. The curve is sketched in Figure.
Ex.29 Sketch the graph of f(x) = xex
Sol. I. The domain is R.
II. The x- and y-intercepts are both 0.
III. Symmetry : None
IV. Because both x and ex become large as x → ∝, we have however, ex → 0 and so we have an indeterminate product that requires the use of L’Hospital’s Rule :
Thus, the x-axis is horizontal asymptote.
V
VI. Because f'(–1) = 0 and f changes from negative to positive at x = –1, f(–1) = –e–1 is a local (and absolute) minimum.
VII. f''(x) = (x + 1)ex + ex = (x + 2)ex Since f''(x) > 0 if x > –2 and f''(x) < 0 if x < –2, f is concave upward on (–2, ∝) and concave downward on (– ∝, – 2). The inflection points in (–2, –2e–2)
VIII. We use this information to sketch the curve in Figure.
Ex.30 Sketch the graph of the function f(x) = x2/3(6 - x)1/3.
Sol. You can use the differentiation rules to check that the first two derivatives are
Since f'(x) = 0 when x = 4 and f'(x) does not exist when x = 0 or x = 6, the critical numbers are 0, 4 and 6.To find the local extreme values we use the First Derivative Test. Since f' changes from negative to positive at 0, f(0) = 0 is a local minimum. Since f' changes from positive to negative at 4, f(4) = 25/3 is a local maximum. The sign of f' does not change at 6, so there is no minimum or maximum there Looking at the expression for f''(x) and noting that x4/3 > 0 for all x, we have f''(x) < 0 for x < 0 and for 0 < x < 6 and f''(x) > 0 for x > 6. So f is concave downward on (-x, 0) and (0, 6) and concave upward on (6, x), and the only inflection point is (6, 0). The graph is sketched in Figure. Note that the curve has vertical tangents at (0, 0) and (6, 0) because |f'(x)| → ∝ as x → 0 and as x→ 6
Ex.31 Plot the following curves :
Sol.
(a) We have whose domain is x ∈ R, and
y' = x2 – 3x + 2 = (x – 1) (x – 2) > 0 for x ∈ (–∝, 1) U (2, ∝) < 0 for x ∈ (1, 2)
⇒ y strictly increases in (–∝, 1) strictly decreases in (1, 2) ; strictly increases in (2, ∝)
Now we have
y (–∝) –∝, y(∝) = ∝
The curve cuts the Y-axis at (0, 6).
The cure cuts the –ve X-axis somewhere between –1and –2, since
The plot of the curve is shown along side.
(b) We have y = x/ln x Whose domain is x ∈ (0, ∝) ~ {1}, and
⇒ y strictly decreases in (0, 1) U (1, e) ; strictly increases in (e, ∝)
The plot of the curve is shown alongside.
(c) We have y = x ln x whose domain is x ∈ (0, ∝), and ⇒ y strictly decreases in (0, e–1) ; strictly increases in (e–1, ∝).
Now, we have
The curve cuts the X-axis at (1, 0). The plot of the curve is shown above.
(d) We have y = lnx/x whose domain is x ∈ (0, ∝), and
⇒ y strictly increases in (0, e); strictly decreases in (e, ∝).
The curve cuts the X-axis at (1, 0). The plot of the curve is shown above.
(e) We have whose domain is x ∈ R ~ {1.7}, and
Now, we have
The curve cuts the Y-axis at (0, 1/7). The curve cuts the X-axis at (–1, 0). The plot of the curve is shown below.
(f) We have
The curve is symmetrical about the X-axis as well as the Y-axis. In the first quadrant the equation of the curve reduces to y = 2–x -1/2
whose plot is shown above.
The complete curve is drawn by taking the mirror image of the above shown curve in the X-axis and the Y-axis as shown alongside
Ex.32 Sketch a possible graph of a function f that satisfies the following conditions :
(i) f'(x) > 0 on (-∞, 1), f'(x) < 0n (1, ∞)
(ii) f''(x) > 0 on (-∞, -2) and (2, ∞), f''(x) < 0 on (-2, 2)
(iii) f(x) = - 2,
f(x) = 0
Sol. Condition (i) tells us that f is increasing on (- ∞, 1) and decreasing on (1, ∞). Condition (ii) says that f is concave upward on (-∞, -2) and (2, ∞), and concave downward on (-2, 2). From condition (iii) we know that the graph of f has two horizontal asymptotes: y = -2 and y = 0.
We first draw the horizontal asymptote y = -2 as a dashed line (see Figure). We then draw the graph of f approaching this asymptote at the far left, increasing to its maximum point at x = 1 and decreasing toward the x-axis at the far right. We also make sure that the graph has inflection points when x = -2 and 2. Notice that we made the curve bend upward for x < -2 and x > 2. and bend downward when x is between -2 and 2.
|
172 videos|503 docs|154 tests
|
FAQs on Increasing and Decreasing Functions & Monotonicity - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the definition of an increasing function? |  |
| 2. How can we determine if a function is increasing or decreasing? |  |
| 3. Can a function be both increasing and decreasing? |  |
| 4. What is the significance of increasing and decreasing functions? |  |
| 5. How can we use the concept of increasing and decreasing functions in real-life applications? |  |

















