NCERT Solutions Class 11 Maths Chapter 2 - Relations and Functions
Q1: Show that the function f: R → R given by f(x) = x3 is injective.
Ans: f : R → R is given as f(x) = x3.
For one – one
Suppose f(x) = f(y), where x, y ∈ R.
⇒ x3 = y3 ...........(1)
Now, we need to show that x = y.
Suppose x ≠ y, their cubes will also not be equal.
⇒ x3 ≠ y3
However, this will be a contradiction to (1).
∴ x = y
Hence, f is injective.
Q2: Given a non-empty set X, consider P(X) which is the set of all subsets of X. Define the relation R in P(X) as follows:
For subsets A, B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify you answer.
Ans: Since every set is a subset of itself, ARA for all A ∈ P(X).
∴ R is reflexive.
Let ARB ⇒ A ⊂ B.
This cannot be implied to B ⊂ A.
For instance, if A = {1, 2} and B = {1, 2, 3}, then it cannot be implied that B is related to A.
∴ R is not symmetric.
Further, if ARB and BRC, then A ⊂ B and B ⊂ C.
⇒ A ⊂ C
⇒ ARC
∴ R is transitive.
Hence, R is not an equivalence relation as it is not symmetric.
Q3: Find the number of all onto functions from the set {1, 2, 3, … , n) to itself.
Ans: Onto functions from the set {1, 2, 3, … , n} to itself is simply a permutation on n symbols 1, 2, …, n. Thus, the total number of onto maps from {1, 2, … , n} to itself is the same as the total number of permutations on n symbols 1, 2, …, n, which is n. 9
Q4: Let A = {−1, 0, 1, 2}, B = {−4, −2, 0, 2} and f, ??: A → B be functions defined by f(x) = x2 − x, x ∈ A 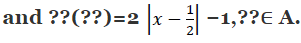
Are f and g equal? Justify your answer. (Hint: One may note that two function f: A → B and ??: A → B such that f(a) = ??(a) ∀ a ∈ A, are called equal functions).
Ans: It is given that A = {-1, 0, 1, 2}, B = {-4, -2, 0, 2}
Also, it is given that f, g : A → B are defined by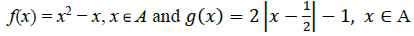
It is observed that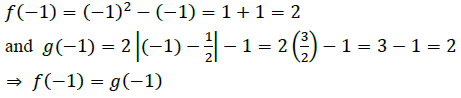
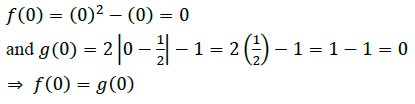
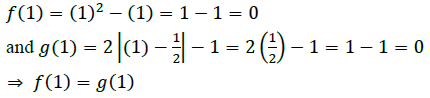
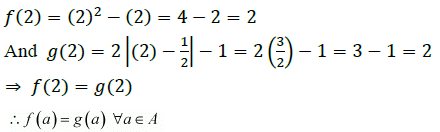
Hence, the functions f and g are equal.
Q5: Let A = {1, 2, 3}. Then number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (a)
Solution. The given set is A = {1, 2, 3}.
The smallest relation containing (1, 2) and (1, 3) which is reflexive and symmetric, but not transitive is given by:
R = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 1), (3, 1)}
This is because relation R is reflexive as (1, 1), (2, 2), (3, 3) ∈ R.
Relation R is symmetric since (1, 2), (2, 1) ∈ R and (1, 3), (3, 1) ∈ R.
But relation R is not transitive as (3, 1), (1, 2) ∈ R, but (3, 2) ∉ R.
Now, if we add any two pairs (3, 2) and (2, 3) (or both) to relation R, then relation R will become transitive.
Hence, the total number of desired relations is one.
Q6: Let A = {1, 2, 3}. Then number of equivalence relations containing (1, 2) is
(a) 1
(b) 2
(c) 3
(d) 4
Ans: (b)
It is given that A = {1, 2, 3}.
The smallest equivalence relation containing (1, 2) is given by,
R1 = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
Now, we are left with only four pairs i.e., (2, 3), (3, 2), (1, 3), and (3, 1).
If we odd any one pair [say (2, 3)] to R1, then for symmetry we must add (3, 2).
Also, for transitivity we are required to add (1, 3) and (3, 1).
Hence, the only equivalence relation (bigger than R1) is the universal relation.
This shows that the total number of equivalence relations containing (1, 2) is two.
Q7: Show that the function f : R → {x ∈ R : – 1 < x < 1} defined by f(x) = x/(x+|x|), x ∈ R is one one and onto function.
Ans: It is given that
f(x)∈(−1,1)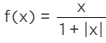
we know that :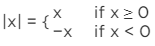
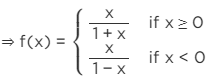
Checking - one-one
case 1: for x≥0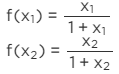
on putting f(x1)=f(x2), we have: 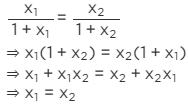
Similarly,
In case 2: for x<0, we get:
x1=x2
Hence, if f(x1)=f(x2), then x1=x2
∴f is one-one.
Checking onto
case 1: for x≥0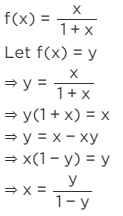
Similarly, in case 2: for x<0 , we have: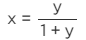
∵y∈(−1,1)
∴ ∀ y∈(−1,1), x is defined.
∴f is onto.
Hence, f(x) is one-one and onto (proved).
Old NCERT Questions:
Q1: Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that gof = fog = IR.
Ans: It is given that f: R → R is defined as f(x) = 10x + 7.
One-one:
Let f(x) = f(y), where x, y ∈ R.
⇒ 10x + 7 = 10y + 7
⇒ x = y
∴ f is a one-one function.
Onto:
For y ∈ R, let y = 10x + 7.
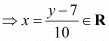
Therefore, for any y ∈ R, there exists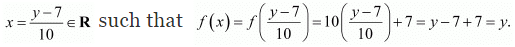
∴ f is onto.
Therefore, f is one-one and onto.
Thus, f is an invertible function.
Let us define g: R → R as f (y) = y-7/10.
Now, we have
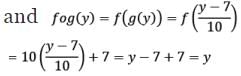
gof = IR, fog = IR
Hence, the required function g: R → R is defined as g(y) = y - 7/10
Q2: Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Ans: It is given that:
One-one:
Let f(n) = f(m).
It can be observed that if n is odd and m is even, then we will have n − 1 = m + 1.
⇒ n − m = 2
However, this is impossible.
Similarly, the possibility of n being even and m being odd can also be ignored under a similar argument.
∴ Both n and m must be either odd or even.
Now, if both n and m are odd, then we have:
f(n) = f(m) ⇒ n − 1 = m − 1 ⇒ n = m
Again, if both n and m are even, then we have:
f(n) = f(m) ⇒ n + 1 = m + 1 ⇒ n = m
∴ f is one-one.
It is clear that any odd number 2r + 1 in co-domain N is the image of 2r in domain N and any even number 2r in co-domain N is the image of 2r + 1 in domain N.
∴ f is onto.
Hence, f is an invertible function.
Let us define g: W → W as:
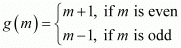
Now, when n is odd:
gof(n) = g(f(n)) = g(n - 1) = n - 1 + 1 = n
And, when n is even:
gof(n) = g(f(n)) = g(n + 1) = n + 1 - 1 = n
Similarly, when m is odd:
fog(m) = f(g(m)) = g(m - 1) = m - 1 + 1 = m
When m is even:
fog(m) = f(g(m)) = g(m + 1) = m + 1 - 1 = m
∴ gof = Iw and fog = Iw
Thus, f is invertible and the inverse of f is given by f—1 = g, which is the same as f.
Hence, the inverse of f is f itself.
Q3: If f: R → R is defined by f(x) = x2 − 3x + 2, find f(f(x)).
Ans: f (f(x)) = f(x2 - 3x + 2)
= (x2 - 3x + 2)2 - 3(x2 - 3x + 2) + 2
= (x4 + 9 x 2 + 4 - 6 x3 - 12x + 4x2) + (- 3x2 + 9x - 6) + 2
= x4 - 6x3 + 10x2 - 3x
Q4: Show that function f: R → {x ∈ R: −1 < x < 1} defined by f(x) = x/1+|x|, x ∈ R is one – one and onto function.
Ans: It is given that f: R → {x ∈ R: −1 < x < 1} is defined as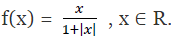
For one – one
Suppose f(x) = f(y), where x, y ∈ R.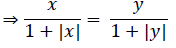
It can be observed that if x is positive and y is negative,
Then, we have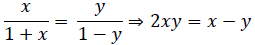
Since x is positive and y is negative:
x > y ⇒ x − y > 0
But, 2xy is negative.
Then, 2xy ≠ x - y.
Thus, the case of x being positive and y being negative can be ruled out.
Under a similar argument, x being negative and y being positive can also be ruled out.
∴ x and y have to be either positive or negative.
When x and y are both positive, we have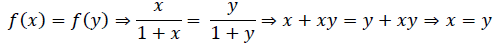
When x and y are both negative, we have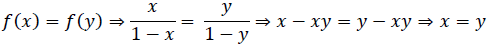
∴ f is one – one.
For onto
Now, let y ∈ R such that −1 < y < 1.
∴ f is onto.
Hence, f is one – one and onto.
Q5: Give examples of two functions f: N → Z and g: Z → Z such that g o f is injective but g is not injective. (Hint: Consider f(x) = x and g(x) = |x|)
Ans: Define f: N → Z as f(x) = x and g: Z → Z as g(x) = |x|.
We first show that g is not injective.
It can be observed that:
g(-1) = |-1| = 1
g(1) = |1| = 1
∴ g(−1) = g(1), but −1 ≠ 1.
∴ g is not injective.
Now, gof: N → Z is defined as gof (x) = g(f(x)) = g(x) = |x|.
Let x, y ∈ N such that gof(x) = gof(y).
⇒ |x| = |y|
Since x and y ∈ N, both are positive.
∴ |x| = |y| ⇒x = y
Hence, gof is injective
Q6: Given examples of two functions f: N → N and ??: N → N such that ?? of is onto but f is not onto.
Ans: Define f: N → N by f(x) = x + 1
We first show that g is not onto.
For this, consider element 1 in co-domain N. It is clear that this element is not an image of any of the elements in domain N.
∴ f is not onto.
Now, gof: N → N is defined by,
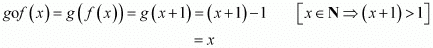
Then, it is clear that for y ∈ N, there exists x = y ∈ N such that gof(x) = y.
Hence, gof is onto.
Q7: Given a non-empty set X, consider the binary operation *: P(X) × P(X) → P(X) given by A * B = A ∩ B ∀ A, B in P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation*.
Ans: It is given the binary operation *:
P(X) × P(X) → P(X) given by A * B = A ∩ B ∀ A, B in P(X)
We know that A ∩ X = A = X ∩ A for all A ∈ P(X)
⇒ A * X = A = X * A for all A ∈ P(X)
Thus, X is the identity element for the given binary operation *.
Now, an element A ∈ P(X) is invertible if there exists B ∈ P(X) such that
A * B = X = B * A [As X is the identity element]
or A ∩ B = X = B ∩ A
This case is possible only when A = X = B.
Thus, X is the only invertible element in P(X) with respect to the given operation*.
Hence, the given result is proved.
Q8: Let S = {a, b, c} and T = {1, 2, 3}. Find F−1 of the following functions F from S to T, if it exists.
(i) F = {(a, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
Ans: S = {a, b, c}, T = {1, 2, 3}
(i) F : S → T is defined as F = {(a, 3), (b, 2), (c, 1)}
⇒ F (a) = 3, F (b) = 2, F(c) = 1
Therefore, F−1: T → S is given by F−1 = {(3, a), (2, b), (1, c)}.
(ii) F : S → T is defined as F = {(a, 2), (b, 1), (c, 1)}
Since F (b) = F (c) = 1, F is not one – one.
Hence, F is not invertible i.e., F−1 does not exist.
Q9: Consider the binary operations*: R ×R → and o: R × R → R defined as a*b = |a - b| and a o b = a, "a,b ∈ R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that "a, b, c ∈ R, a*(b o c) = (a * b) o (a * c). [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over *? Justify your answer.
Ans: It is given that *: R × R → and o: R × R → R is defined as
a * b = |a - b| and a o b = a, "a, b ∈ R.
For a, b ∈ R, we have:
a * b = |a - b|
b * a = |b - a| = |-(a - b)| = |a - b|
∴ a * b = b * a
∴ The operation * is commutative.
It can be observed that,
(1 * 2) * 3 = (|1 - 2|) * 3 = 1 * 3 = |1 - 3| = 2
and 1 * (2 * 3) = 1 * (|2 - 3|) = 1 * 1 = |1 - 1| = 0
∴ (1 * 2) * 3 * 1 * (2 * 3) where 1, 2, 3 ∈ R.
Hence, the operation * is not associative.
Now. consider the operation o
It can be observed that 1 o 2 = 1 and 2 o 1 = 2.
∴ 1 o 2 ≠ 2 o 1 where 1, 2 ∈ R.
Hence, the operation o is not commutative.
Let a.b.c ∈ R. Then, we have
(a o b)o c = a o c = a
and a o (b o c) = a o b = a
∴ a o b) o c = a o (b o c). where a, b, c ∈ R
Hence, the operation o is associative.
Now. let a, b, c ∈ R. then we have
a * (b o c) = a * b =|a — b|
(a * b) o (a * c) = (|a — b|) o (|a — c|) = |a — b|
Hence, a * (b o c) = (a * b)o (a * c).
Now, 1 o (2 * 3) = 1 o (|2 - 3|) = 1 o 1 = 1
(1 o 2) * (1 o 3) = 1 * 1 = |1 - 1| = 0
∴ 1 o (2 * 3) # (1 o 2) * (1 o 3) where 1, 2, 3 ∈ R
Hence, the operation o does not distribute over *.
Q10: Given a non -empty set X, let *: P(X) × P(X) → P(X) be defined as A * B = (A − B) ∪ (B − A), ∀ A, B ∈ P(X). Show that the empty set Φ is the identity for the operation * and all the elements A of P(X) are invertible with A−1 = A.
(Hint: (A − Φ) ∪ (Φ − A) = A and (A − A) ∪ (A − A) = A * A = Φ).
Ans: It is given that *: P(X) × P(X) → P(X) is defined as A *B = (A -B) U (B - A) ∀ A, B ∈ P (X).
Let A ∈ P(X). Then, we have
A * Φ = (A - Φ) U (Φ - A)= A U Φ = A
Φ * A = (Φ - A) U (A - Φ) = Φ U A = A
∴ A * Φ = A = Φ * A for all A ∈ P(X)
Thus, Φ is the identity element for the given operation *.
Now, an elements A ∈ P(X) will be invertible if there exists B ∈ P(X) such that
A * B = Φ = B * A. [As Φ is the identity element]
Now. we observed that
A * A = (A - A) U (A - A) = Φ U Φ = 0 for all A ∈ P(X).
Hence, all the elements A of P(X) are invertible with A-1 = A.
Q11: Define a binary operation *on the set {0, 1, 2, 3, 4, 5} as
Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 − a being the inverse of a.
Ans: Let X = {0, 1, 2, 3, 4, 5}.
The operation * on X is defined as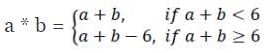
An element e ∈ X is the identity element for the operation *. if
a * e = a = e * a for all a ∈ X
For a ∈ X, we have
a * 0 = a + 0 = a [a ∈ X ⇒ a + 0 < 6 ]
0 * a = 0 + a = a [a ∈ X ⇒ 0 + a < 6 ]
∴ a * 0 = a = 0 * a for all a ∈ X
Thus, 0 is the identity element for the given operation *.
An element a ∈ X is invertible if there exists b ∈ X such that a * b = 0 = b * a.
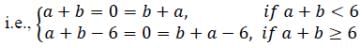
⇒ a = - b or b = 6 - a
But, X = {0, 1, 2, 3, 4, 5} and a, b ∈ X. Then, a ≠ -b.
∴ b = 6 - a is the inverse o f a for all a E X .
Hence, the inverse o f an element a ∈ X. a ≠ 0 is 6 - a i.e., a-1 = 6 - a.
Q12: Let f: R → R be the Signum Function defined as
and g: R → R be the Greatest Integer Function given by g(x) = [x], where [x] is greatest integer less than or equal to x. Then does fog and gof coincide in (0, 1]?
Ans: It is given that,
f: R → R is defined as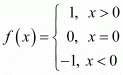
Also, g: R → R is defined as g(x) = [x], where [x] is the greatest integer less than or equal to x.
Now, let x ∈ (0, 1].
Then, we have:
Thus, when x ∈ (0, 1), we have fog(x) = 0and gof (x) = 1.
Hence, fog and gof do not coincide in (0, 1].
Q13: Number of binary operations on the set {a, b} are
(a) 10
(b) 16
(c) 20
(d) 8
Ans: (b)
Solution. A binary operation * on {a, b} is a function from {a, b} × {a, b} → {a, b} i.e., * is a function from {(a, a), (a, b), (b, a), (b, b)} → {a, b}.
Hence, the total number of binary operations on the set {a, b} is 24 i.e., 16.
|
203 videos|307 docs|139 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 2 - Relations and Functions
| 1. What are the types of relations in mathematics? |  |
| 2. How are functions different from relations? |  |
| 3. How do you determine if a relation is reflexive? |  |
| 4. What is the difference between a one-to-one function and an onto function? |  |
| 5. How do you find the composition of two functions? |  |






















