Lines and Angles Class 7 Notes Maths Chapter 6

Take a moment to look around the room you're in. What do you notice? Maybe a table, a chair, a wall clock, a laptop, or even a staircase. Now, glance outside—there are trees, roads, buildings, and electric poles. Did you know that all these things are made up of simple shapes like lines and angles?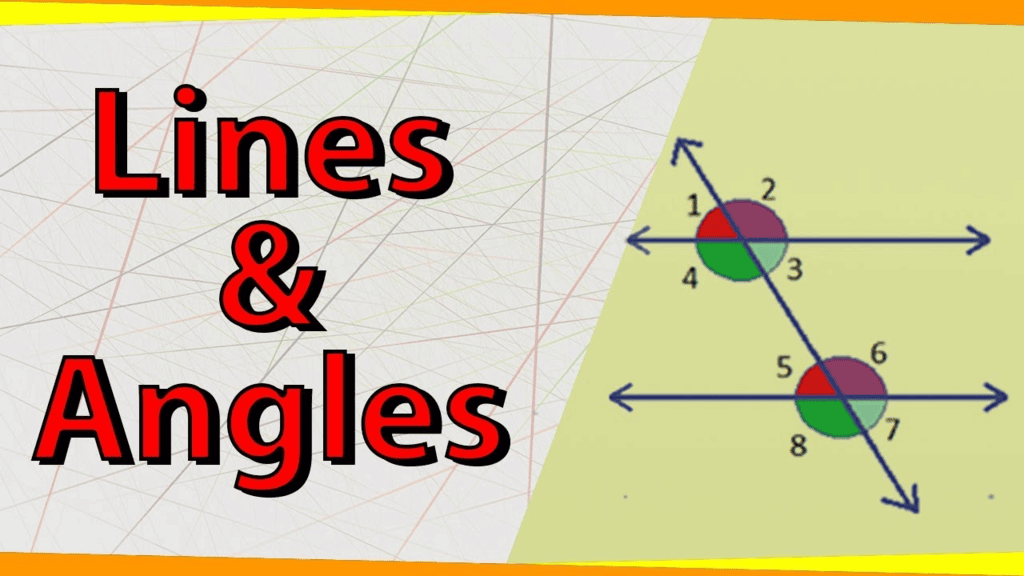
Let's dive into the world of lines and angles to understand how they form the very objects we see every day.

Real-Life Examples of Lines and Angles

(ii) Railway Tracks: When we observe the railway tracks, they run in straight lines extending on both directions.

(iii) Laptop: If we observe, the adjacent sides of the laptop, they form an angle between them.

(iv) Ladder: The two legs of a ladder resemble straight lines. The two legs join at one point and the opening between them is the angle formed by these legs.

(v) Open Door: What happens when you open a door? As soon as you open the door an angle is formed between the edge of the door and the threshold of the panel.

Door 

Important Terms Related to Lines and Angles

• Point: An exact location that has no size i.e., no length, no width, no depth, the only position is called a point. A point is denoted by a dot (.)
  If you take an ink pen and put a dot on paper using that, then that dot represents a point.
• Line segment: A collection of points with two fixed endpoints is called a line segment. A line segment AB is denoted by The length of a line segment is fixed.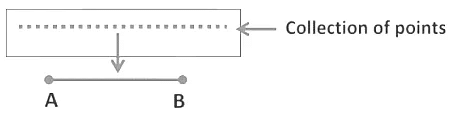
• Ray: A part of a line with one fixed point and extends endlessly from the other end is called a ray. Ray AB is denoted by The length of a ray is infinite.
  
  Ray
• Line: A-Line is a collection of points going endless in both directions along the straight path. Line AB is denoted by The length of a line is infinite.
  
  Straight Line  

What is an Angle?

When two rays originate from a common point, then the turn between two rays around the common point or vertex is called the angle between the two rays.

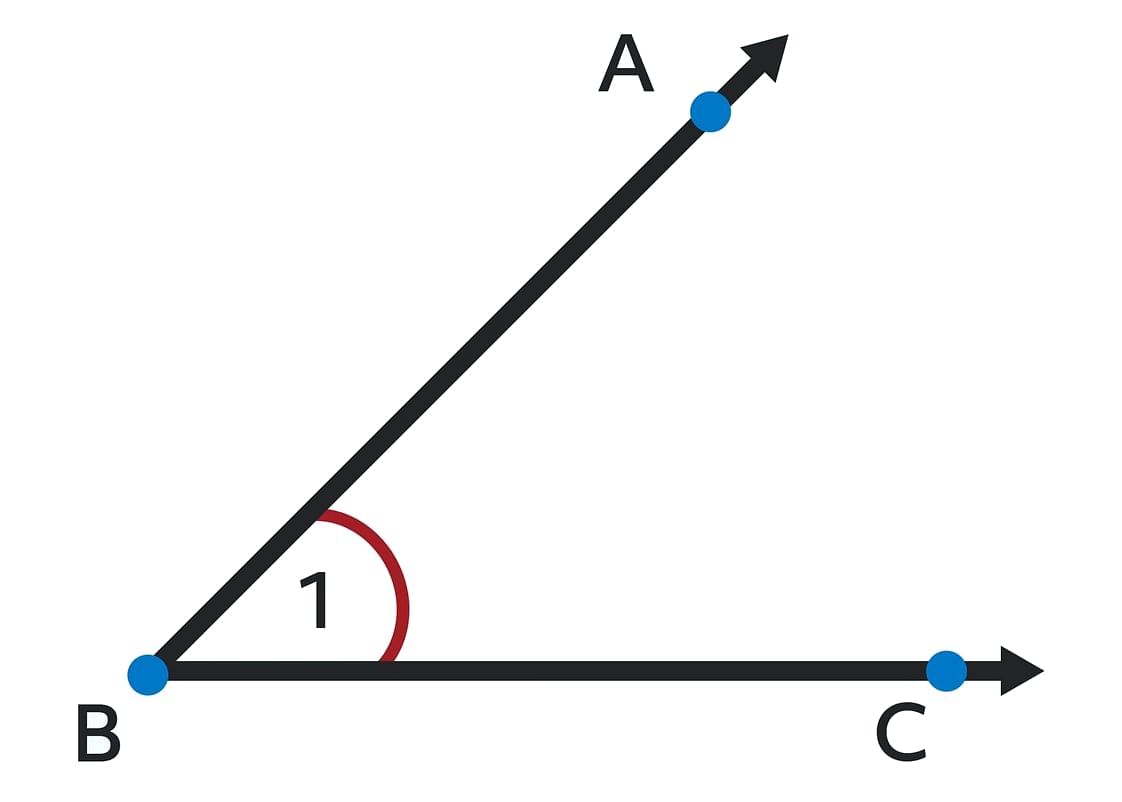Formation of Angle

• The two rays joining to form an angle are called arms of an angle and the point at which two rays meet to form an angle is called the vertex of the angle.

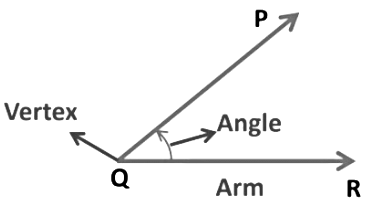
In the above figure, two rays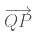and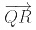are the arm of an angle that meet at a common initial point Q (vertex)and form a ∠PQR. The measure of the angle PQR is written as ∠PQR but instead of writing this, we can simply write it as ∠PQR.

Types of Angles

Understanding the different types of angles is crucial in geometry, as they are fundamental to many geometric concepts and real-world applications.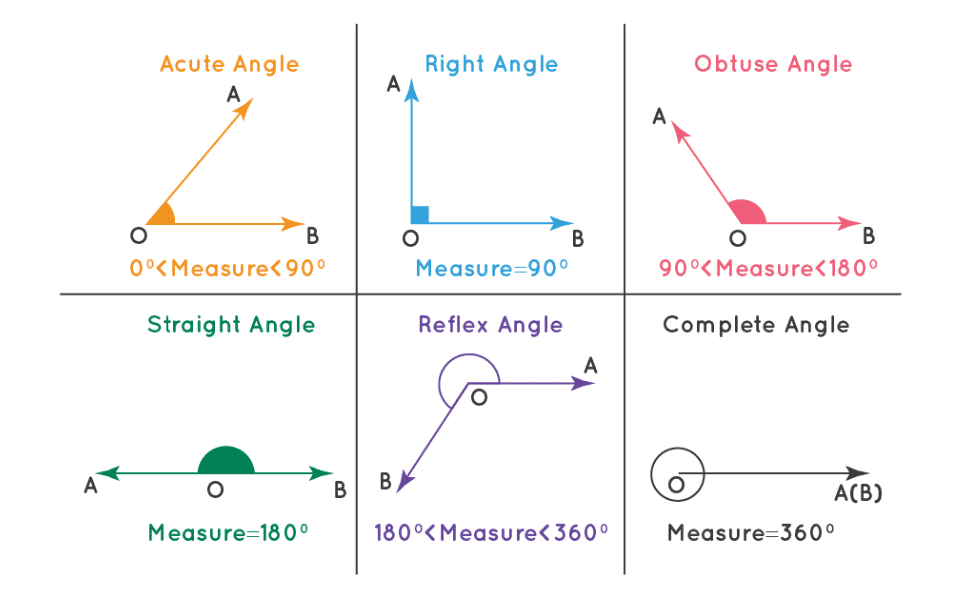
Types of Angles

1. Acute Angle

An acute angle is an angle that measures greater than 0° but less than 90°. It is the smallest type of angle, often seen in sharp corners.

• Example: The angles in a slice of pizza or the hands of a clock at 10:10.

2. Right Angle

A right angle is exactly 90°. It represents a quarter turn and is often associated with perpendicular lines.

• Example: The corner of a square or rectangle.

3. Obtuse Angle

An obtuse angle is one that measures greater than 90° but less than 180°. These angles appear wider and are more open than acute angles.

• Example: The angle formed by the hands of a clock at 10:15.

4. Straight Angle

A straight angle is exactly 180°. It forms a straight line, representing a half turn.

• Example: The angle formed when two people standing back to back extend their arms in opposite directions.

5. Reflex Angle

A reflex angle measures greater than 180° but less than 360°. Reflex angles appear larger and more open than obtuse angles.

• Example: The angle formed by the hands of a clock at 8:20.

6. Complete Angle

A complete angle is exactly 360°. It represents a full turn or a complete circle.

• Example: The angle formed by the hands of a clock at 12:00.

Related Angles

1. Complementary Angles

• When the sum of the measures of two angles is 90°, the angles are called complementary angles.
• Whenever two angles are complementary, each angle is said to be the complement of the other angle.

Complementary Angles

Here,
∠PQS + ∠SQR= 50° + 40° = 90°
In the above figure, we see that the sum of two angles is 90°.

Hence, ∠PQS and ∠SQR are complementary angles. And ∠PQS and ∠SQR are said to be complements of each other.
Example: Are the given angles complementary?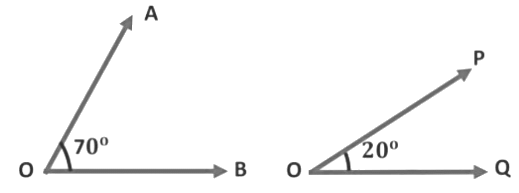
In the given figure,
∠AOB = 70°and ∠POQ = 20°
∠AOB + ∠POQ = 70° + 20° = 90°
Therefore, ∠AOB and ∠POQ are complementary angles.

2. Supplementary Angles

• Two angles are said to be supplementary if the sum of their measure is equal to 180°.
• When two angles are supplementary, each angle is said to be the supplement of the other
  
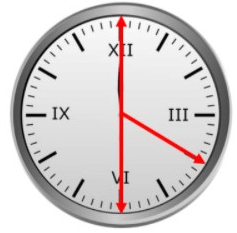  Clock 

Example: Clock: The two angles formed by the hands of the above clock are supplementary.

• The measure of two angles 120° and 60° are given and when we add up that angles we get 180°.
  120° + 60° = 180°.
• Hence, we can say that they are supplementary angles or supplements of each other.

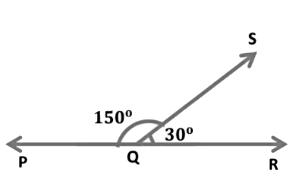Supplementary Angle

Here,
∠PQS + ∠SQR = 150° + 30° = 180°
In the above figure, we see that the sum of two angles is 180°.

Hence, ∠PQS and ∠SQR are supplementary angles, and ∠PQS and ∠SQR are said to be supplements of each other.

Example: The following ∠AOB and ∠POQ are supplementary angles or not?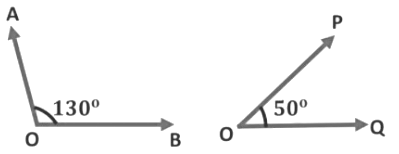
Supplementary Angle

Sol: In the given figure,
∠AOB + ∠POQ = 130° + 50° = 180°
∠AOB + ∠POQ = 180°
∴ ∠AOB and ∠POQ are supplementary angles. Or
∠AOB and ∠POQ are said to be supplements of each other.

3. Adjacent Angles

These angles are such that:

(i) they have a common vertex.

(ii) they have a common arm.

(iii) the non-common arms are on either side of the common arm.

Such pairs of angles are called adjacent angles. 

Note: Adjacent angles have a common vertex and a common arm but no common interior points.

Example: In the following figure angles marked with 1 and 2 are they adjacent? If not give a reason for that.
Adjacent Angle

Solution:

In figure number (i)
(i) We see ∠PQS and ∠SQR have a common arm QS.
They have a common vertex Q.
They do not have a common interior point.
Hence, ∠PQS and ∠SQR are adjacent angles

In figure number (ii)
(ii) We see ∠RQS and ∠SQP have a common arm QS.
They have a common vertex Q.
They do not have a common interior point
Hence, ∠RQS and ∠SQP are adjacent angles

In figure number (iii)
(iii) We see ∠PTS and ∠SQR have a common arm QS.
They do not have a common vertex.
They do not have a common interior point.
The above figure does not satisfy all the conditions for being adjacent angles.
Hence, ∠PTS and ∠SQR are not adjacent angles.

Pairs of Lines

1. Intersecting Lines

Two lines are said to be intersecting when they cross each other at one point only and the point at which they intersect is called the point of intersection.

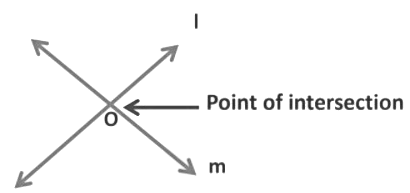Here, two lines l and m intersect each other at point O, and point O is called the point of intersection.

2. Transversal Line

A line that intersects two or more lines in a plane at distinct points is called a transversal line.

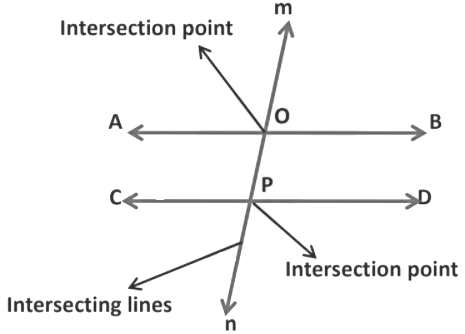
• Here, line mn intersects two lines AB and CD at two distinct points O and P respectively. 
• Hence, line mn is called the transversal line and points O and P are called the points of intersection.

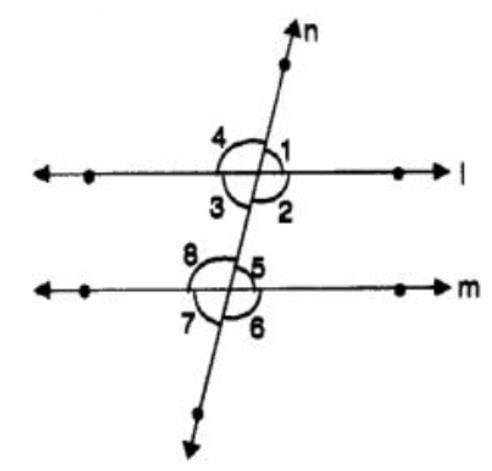
3. Angles made by a Transversal

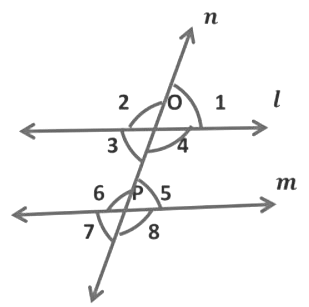
Here, the two lines l and m are intersected by a transversal n at points O and P respectively. We see that four angles are formed at each point O and P, namely ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, and ∠8.

Example: In the figure given below, l || m and ∠1 = 53°. Find ∠6 and ∠7.

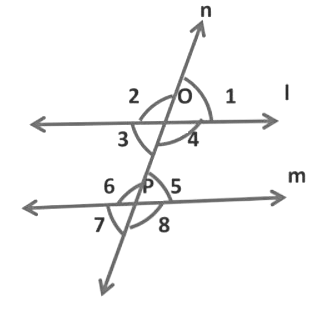
We have,
∠1 = ∠3 [Vertically opposite angles]
∠3 = ∠7 [Corresponding angles]
∴ ∠1 = ∠7
→ ∠7 = 53° ∵ ∠1 = 53° (Given)
∠6 + ∠7 = 180° [Linear pair]
∠6 + 53° = 180°
∠6 + 53° − 53° = 180° − 53°
∠6 = 127°
Thus, ∠6 = 127° and ∠7 = 53°

4. Transversal of Parallel Lines

If two lines lying in the same plane do not intersect when produced on either side, then such lines are said to be parallel to each other.

Here, lines l and m are parallel to each other, and transversal n intersects line l and m at point O and P respectively.

When the two parallel lines l and m are cut by a transversal n, then obtained the following relations:
(i) When a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.
When line n intersects two parallel lines l and m, then we see that each pair of alternate interior angles is equal.
∴ ∠ 3 = ∠5, ∠4 = ∠6

(ii) When a transversal intersects two parallel lines, each pair of alternate exterior angles are equal.

When line n intersects two parallel lines l and m, then we see that each pair of alternate exterior angles is equal.
∴ ∠ 2 = ∠8, ∠1 = ∠7

(iii) When a transversal intersects two parallel lines, each pair of corresponding angles are equal.
When line n intersects two parallel lines l and m, then we see that each pair of corresponding angles is equal.
∴ ∠3 = ∠7, ∠2 = ∠6, ∠ 1 = ∠5, and ∠4 = ∠8

(iv) When a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal are supplementary
When line n intersects two parallel lines l and m, then we see that each pair of interior angles on the same side of the transversal are supplementary.
In the above figure, ∠ 3 = ∠4 .....Linear pair of angles
We know sum of the linear pair of angles is 180° ∴ ∠ 3 + ∠4 = 180°
But, ∠4 = ∠6 ...Pair of alternate interior angles Therefore, we can say that ∴ ∠ 3 + ∠6 = 180°
Similarly, ∠4 + ∠5 = 180°

Example: In the given figure l || m, ∠1 = 55°. Find ∠5, ∠6, and ∠7.

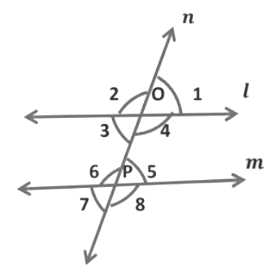
We have,
∠ 1 = ∠5 .....Corresponding angles
∴ ∠ 5 = 55° [∵ ∠1 = 55°]
∠5 = ∠7 .....Vertically opposite angles
∴ ∠7 = 55° [∵ ∠5 = 55°]
Now,
∠ 6 + ∠7 = 180°.....Linear pair of angles
∠ 6 + 55° = 180°
∠ 6 + 55° − 55° = 180° − 55°
∠ 6 = 180° − 55°
∠ 6 = 125°
Thus, ∠ 5 = 55°, ∠ 6 = 125°and ∠7 = 55°

Checking for Parallel Lines

Some special pairs of angles can be used to test if the lines are parallel or not.

(i) When a transversal intersects two parallel lines, such that if any pair of corresponding angles are equal, then the lines are parallel.

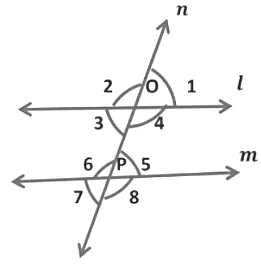
In the given figure, transversal n intersects two lines l and m in such a way that,
∠3 = ∠7, ∠2 = ∠6, ∠ 1 = ∠5, and ∠4 = ∠8 ...(Pairs of corresponding angles are equal)
Hence, we can say that lines are parallel.

(ii) When a transversal intersects two parallel lines, such that if any pair of alternate interior angles are equal, the lines have to be parallel.

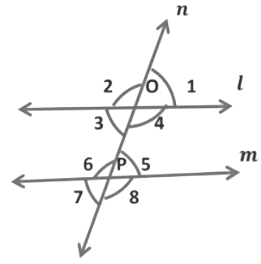
In the given figure, transversal n intersects two lines l and m in such a way that,
∠ 3 = ∠5, ∠4 = ∠6 ... (Alternate interior angles are equal)

Hence, we can say that lines are parallel.

(iii) When transversal intersects two parallel lines, such that if any pair of alternate exterior angles are equal, the lines have to be parallel.

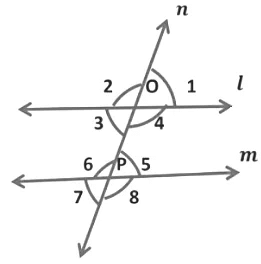
In the given figure, transversal n intersects two lines l and m in such a way that,
∠1 = ∠7, ∠2 = ∠8 ... (Alternate exterior angles are equal)

Hence, we can say that lines are parallel.

(v) When transversal intersects two parallel lines, such that if any pair of interior angles on the same side of the transversal are supplementary, the lines have to be parallel.

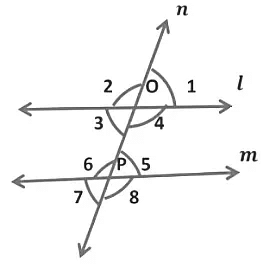
In the given figure, transversal n intersects two lines l and m in such a way that, ∠ 3, ∠6 and ∠4, ∠5 ...Pairs of co-interior angles or angles on the same sides of the transversal
Hence,
∠ 3 + ∠6 = 180° and
∠4 + ∠5 = 180°
Hence, we can say that lines are parallel.

Example: Find whether AB || CD.

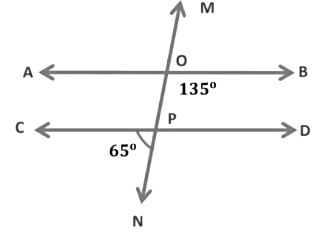
In the given figure,
∠CPN = ∠OPD = 65°...Vertically opposite angles
∠BOP + ∠OPD = 180°
Thus, the sum of co-interior angle is 180°
Hence,
135° + ∠OPD = 180°
∠OPD = 180° − 135°
∠OPD = 45°
Therefore, AB || CD