Congruence of Triangles Class 7 Notes Maths
7. Congruence of Triangles
Congruence of Plane Figures
If two objects are of exactly the same shape and size, they are said to be congruent.
If two objects are of exactly the same shape and size, they are said to be congruent.
The relation between two congruent objects is called congruence. The method of superposition examines the congruence of plane figures, line segments and angles. Two plane figures are congruent if each, when superimposed on the other, covers it exactly.
If two line segments have the same or equal length, they are congruent. Also, if two line segments are congruent, then they have the same length.
Eg: Two line segments, say, PQ & RS are congruent if they have equal lengths. We write this as
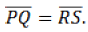
If two angles have the same measure, they are congruent. Also, if two angles are congruent, their measures are the same.
Eg:
Two angles, say, ∠PQR and ∠XYZ, are congruent if their measures are equal. We write this as or as m∠PQR = m∠XYZ. However, commonly, we write
Page 25
A plane figure is any shape that can be drawn in two dimensions.
Congruence of Plane Figures
A plane figure is any shape that can be drawn in two dimensions.
A plane figure is any shape that can be drawn in two dimensions.
Examples: Rectangle, square, triangle, rhombus, etc.
If two objects are of exactly the same shape and size, they are said to be congruent, and the relation of the two objects being congruent is called congruence. Or we can state it as: "Two plane figures are congruent if each, when superimposed on the other, covers it exactly." Congruence is denoted by .
However, how do you check if two figures drawn on a paper are congruent or not? One method is to make a traced copy of one of the figures on a tracing paper and place it over the other.
The other method is to cut out one of these figures and place it over the other. However, take care not to twist, bend or stretch the traced or cut image.
Page 26

If two angles have the same measure, then they are congruent. Also, if two angles are congruent, then their measures are the same. If two angles are congruent, then the lengths of their arms do not matter.
Criteria for Congruence of Triangles
Two triangles are congruent if all the sides and all the angles
Congruence of triangles:
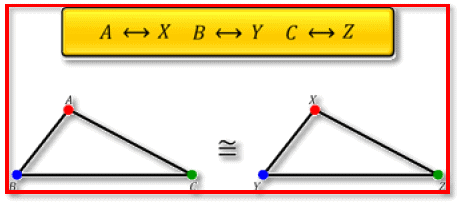
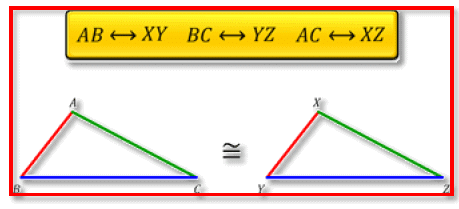
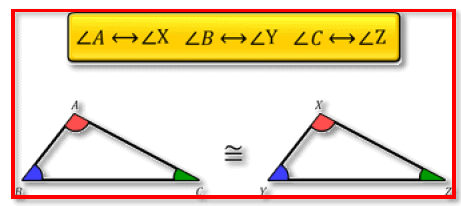
Consider triangles ABC and XYZ. Cut triangle ABC and place it over XYZ. The two triangles cover each other exactly, and they are of the same shape and size. Also notice that A falls on X, B on Y, and C on Z. Also, side AB falls along XY, side BC along YZ, and side AC along XZ. So, we can say that triangle ABC is congruent to triangle XYZ. Symbolically, it is represented as
So, in general, we can say that two triangles are congruent if all the sides and all the angles of one triangle are equal to the corresponding sides and angles of the other triangle.
Page 27
In two congruent triangles ABC and XYZ, the corresponding vertices are A and X, B and Y, and C and Z, that is, A corresponds to X, B to Y, and C to Z. Similarly, the corresponding sides are AB and XY, BC and YZ, and AC and XZ. Also, angle A corresponds to X, B to Y, and C to Z. So, we write ABC corresponds to XYZ.
We can tell if two triangles are congruent using 4 axioms: SAS axiom, ASA axiom, SSS axiom and RHS axiom.
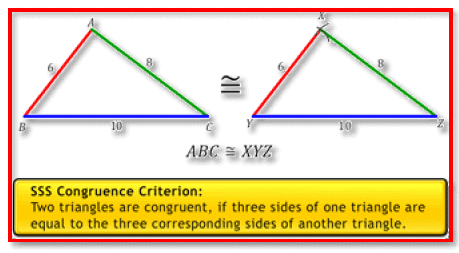
SSS congruence criterion: Two triangles are congruent if three sides of one triangle are equal to the three corresponding sides of the other triangle.
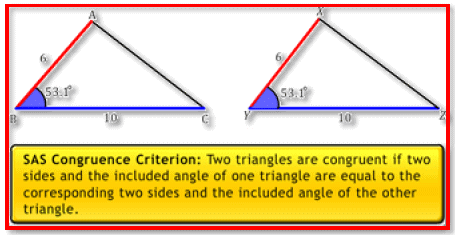
SAS congruence criterion: Two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle.
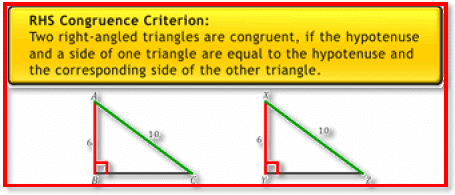
RHS congruence criterion: Two right-angled triangles are congruent if the hypotenuse and a side of one triangle are equal to the hypotenuse and the corresponding side of the other triangle.
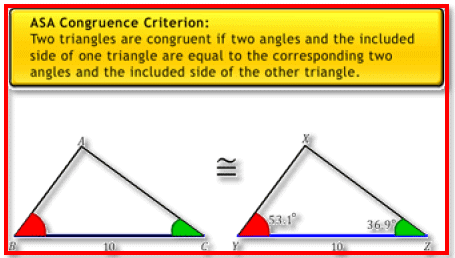
ASA congruence criterion: Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
Page 28
We can tell if two triangles are congruent using 4 axioms: SAS axiom, ASA axiom, SSS axiom and RHS axiom.
SSS congruence criterion: Two triangles are congruent if three sides of one triangle are equal to the three corresponding sides of the other triangle.
SAS congruence criterion: Two triangles are congruent if two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of the other triangle.
RHS congruence criterion: Two right-angled triangles are congruent if the hypotenuse and a side of one triangle are equal to the hypotenuse and the corresponding side of the other triangle.
ASA congruence criterion: Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle.
|
78 videos|457 docs|39 tests
|
FAQs on Congruence of Triangles Class 7 Notes Maths
| 1. What is congruence of triangles? |  |
| 2. What are the criteria for congruence of triangles? |  |
| 3. How is congruence of triangles used in real life? |  |
| 4. What is the importance of congruence of triangles in mathematics? |  |
| 5. How can I use congruence of triangles to solve problems in geometry? |  |

















