Polygons with Solved Examples | Quantitative Aptitude (Quant) - CAT PDF Download
A closed plane figure made up of several line segments that are joined together is called a polygon. The sides do not cross each other. Exactly two sides meet at every vertex.
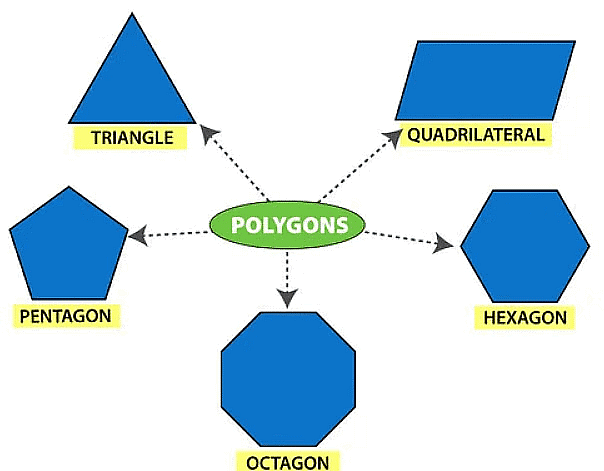
Types of Polygons:
1. Regular: All angles are equal and all sides are of the same length. Regular polygons are both equiangular and equilateral.
2. Equiangular: All angles are equal.
3. Equilateral: All sides are of the same length.
Properties of Polygon

Quadrilaterals
A polygon with 4 sides, is a quadrilateral
1. In a quadrilateral, sum of the four interior angles is equal to 360° and also the sum of exterior angles
equal to 360°.
2. On the properties, quadrilaterals have been named differently, as given below.
1. Trapezium
(a) When one pair of opposite sides is parallel and no condition for other pair of opposite sides, then the
quadrilateral is Trapezium.
(b) When the non – parallel sides are equal in length then
the trapezium formed is “isosceles trapezium”.
(c) The diagonals of isosceles trapezium are equal in
length but do not bisect.

Example 1:
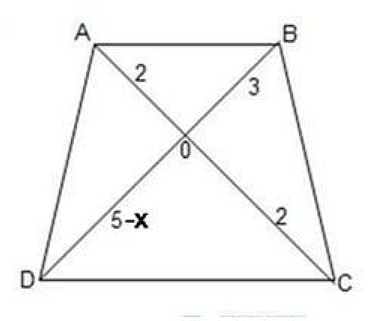
In the figure shown, ABCD is a trapezium. What is the value of x?
A. −11/3
B. -2
C. 2
D. 3
E. 11
Answer: Option C
Solution:
∆ABO and ∆DOC are similar triangle because AB and CD are parallel by property of Trapezium
i.e.
Angle AOB = angle DOC
Angle BAO = angle OCD
Angle ABO = angle ODC
Ratio of corresponding sides (sides opp to equal angles) are equal in case of similar triangle
i.e. AO / OC = BO / OD
i.e. 2 / 2 = 3 / (5-x)
i.e. (5-x) = 3
i.e. x = 2
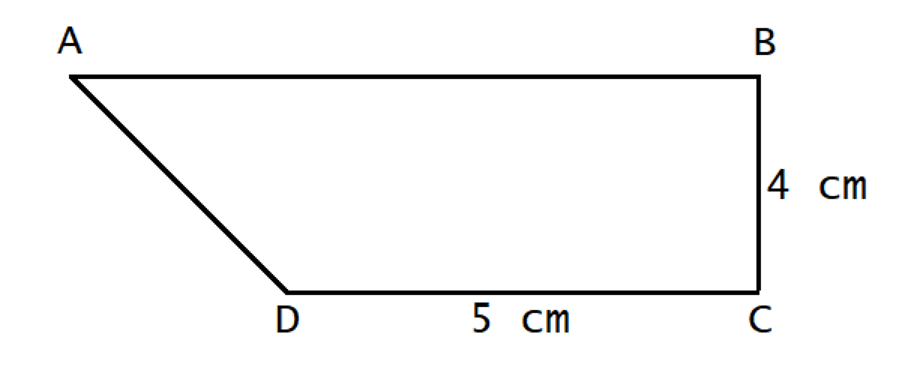
Example 2: In a trepezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45°. If DC = 5 cm, BC = 4 cm, the area of the trepezium in sq. cm is
Answer: 28
Solution:
Let's draw the Trapezium.
Now drop a perpendicular from D onto AB touching AB at E.
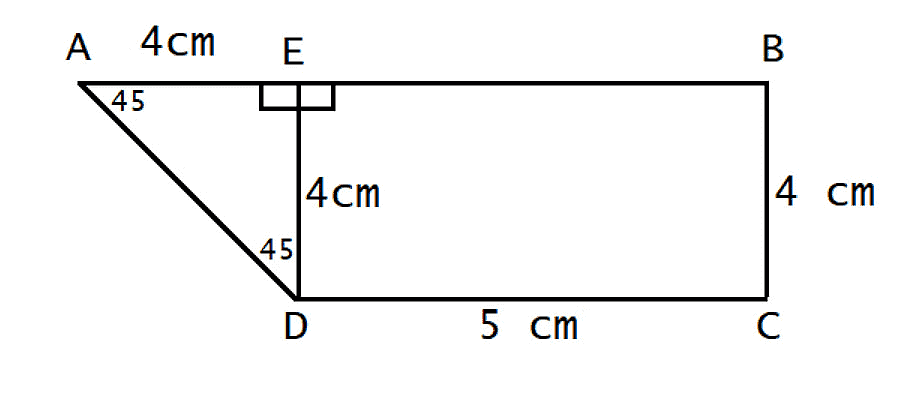
In ΔAED, ∠AED = 90°, ∠DAE = 45°, therefore ∠EDA = 45°.
Clearly ΔAED is an isosceles right triangle and Quadrilateral BCDE is a rectangle.
Therefore, BC = DE = 4cm.
Since ΔAED is an iscoceles triangle, AE = ED = 4cm.
Area of the Trepezium = Area of ΔAED + Area of Rectangle BCDE
Area of the Trepezium = 12 × AE × ED + DC × BC
Area of the Trepezium = 12 × 4 × 4 + 5 × 4
Area of the Trepezium = 8 + 20
Area of the Trepezium = 28 cm2
2. Parallelogram
(a) Opposite sides are equals and parallel.
(b) Opposite angles are equal.
(c) Diagonals bisect each other
(d) Each diagonal divides the parallelogram into two triangles of equal area.
(e) Sum of any two adjacent angles is 180°.

Example: In the figure the area of the parallelogram is
A. 40
B. 24 √3
C. 72
D. 48 √3
E. 96
Answer: Option D
Solution:
Given
In this question, we are given
• The diagram of a parallelogram, where the adjacent sides are of length 8 and 12
• One angle between the sides is 60°
To Find
We need to determine
• The area of the parallelogram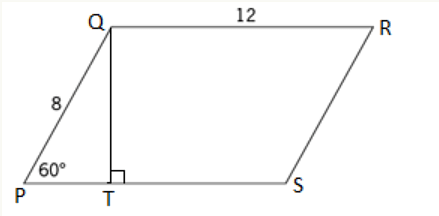
Let us assume the parallelogram is PQRS, and QT is the perpendicular dropped from point Q to the side PS.
• Hence, we can say that PQT is a 30°-60°-90° triangle, and the side ratio is 1: √3: 2.
• QT: PQ = √3: 2
Or, QT = (√3)/2 * PQ = (√3)/2 * 8 = 4√3
• Therefore, the area of the quadrilateral = PS * QT = 12 * 4√3 = 48√3 (PS = QR)
Hence, the correct answer is option D.
3. Rhombus
(a) All sides are equal, opposite sides are parallel.
(b) Opposite angles are equal.
(c) Diagonals bisect each other at right-angled. But they are not equal.
(d) Each diagonal divides the rhombus into two triangles of equal area.
(e) Area = 

Example1:
The length of a side of a rhombus is a two-digit number. If the digits of this number are interchanged the new number formed is one tenth the original number. The sum of these two number is 11. The side and one of the diagonals of the rhombus are in the ratio 5 : 6. What is the area of the rhombus (in square units)?
(A) 49 sq. units
(B) 54 sq. units
(C) 92 sq. units
(D) 96 sq. units
(E) 98 sq. units
Answer: (D)
Solution:
Length of side is 2 digit number and on reversing the digits, you get one tenth of the number.
Say if the side were 21, you would reverse the digits to get 12 which is more than half of 21.
Even if the side were 91, you would reverse the digits to get 19 which is till about a fifth. The only way you would get a tenth is if the number ends with a 0 i.e. if the side is 10 or 20 or 30 etc so that on reversing the digits, you will get 1 or 2 or 3 (one tenth of the number)\
Sum of the numbers is 11 which means the side length is 10.
Ratio of side: diagonal = 5 : 6
Since side is 10, diagonal is 12.
A rhombus is a kite shape with all sides equal and diagonals perpendicular bisectors. So you get 4 equal right triangles with side 10 as hypotenuse and one leg as 6 (half the diagonal). This will give us a multiple of 3-4-5 triangle so the other half diagonal will be 8.
Area of triangle = (1/2)*6*8 = 24
Area of rhombus = 4 * 24 = 96
Example 2: Is quadrilateral q a rhombus?
(1) Quadrilateral q has four equal sides
(2) Quadrilateral q has four equal angles
A. Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient to answer the question asked.
B. Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient to answer the question asked.
C. BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
D. EACH statement ALONE is sufficient to answer the question asked.
E. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Answer: A.
Definition: rhombus is a quadrilateral with all four sides equal in length.
(1) Quadrilateral q has four equal sides --> quadrilateral q is a rhombus. Sufficient.
(2) Quadrilateral q has four equal angles. Quadrilateral q could be a rectangle (which is not a square, thus not a rhombus) as well as a square, thus a rhombus. Not sufficient.
4. Rectangle
(a) Pair of opposite sides equal.
(b) Each angle is 90o.
(c) Diagonals are equal and bisect each other (not at right angles).
(d) Length of diagonal = 

Example: A rectangle is inscribed in a circle of radius r. If the rectangle is not a square, which of the following could be the perimeter of the rectangle?
A. 2r√3
B. 2r(√3+1)
C. 4r√2
D. 4r√3
E. 4r(√3+1)
Answer: B
Solution:
Since the radius of the circle is r, the diameter must be 2r. Now imagine the rectangle. The diameter must be the hypotenuse of the right angled triangle of the rectangle. Say, if its sides are a and b,
(2r)2=a2+b2=4r2
So when you square a and b and sum them, you should get 4r2
The given options are the perimeter of the rectangle i.e. 2(a+b). So we ignore 2 of the options and try to split the leftover into a and b.
The obvious first choices are options (B) and (E) since we can see that we can split the sum into 3 and 1.
a+b= r√3+r
5. Square
(a) All sides are equal and angles equal.
(b) Diagonals equal and bisect at 90O.
(c) When it is inscribed in a circle, the diagonal of square is equal to
The diameter of the circle. But when circle is inscribed in a square,the side of the square is equal to diameter of the circle.

Example: Squares are placed one inside another, leaving a strip of uniform width around each square. If
PQ = 2√2 units, QR = 2 units and RS = 10 units, what is the area of the shaded region?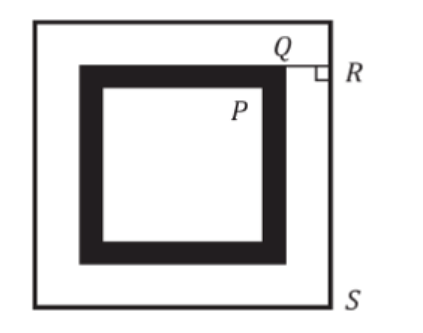
(A) 16
(B) 28
(C) 32
(D) 48
(E) 64
Solution:
GIVEN:
Width of strip is uniform around each square. PQ = 2√2 units, QR = 2 units and RS = 10 units.

First of all we will draw a perpendicular PU from vertex P on side QT.
So in Triangle PUQ:-
Let PU = QU = x units. (width of the shaded region)
By applying Pythagoras theorem,
(PQ)2 = (PU)2 + (QU)2
(2√2)2 = x2 + x2
2x2 = 8
x2 = 4
x = 2 units.
As, RS =10 units.
So, QT = RS – QR = 10 – 2 = 8 units.
And, PV = QT – 2(PU) = 8-2(2) =4 units.
Area of Shaded region = (Area of square with side QT) – (Area of square with side PV) = (8 × 8) – (4 × 4)= 48 sq units.
The correct answer is D.
Important Results
If we join the mid-point of a quadrilateral we get a parallelogram and the mid-point of parallelogram will give a rectangle. If we again in join the mid-point of rectangle we get a rhombus and the mid point of rhombus will give you a square.

Sometimes we get questions in which a quadrilateral is inscribed in a circle. Hence, it is important to understand properties of circles as well in order to solve such question.
Circles
If O is a fixed point in a given plane, the set of points in the plane which are at equal distances from O will form a circle.
Parts of circle
In the figure below O is the centre of the circle of radius OM and diameter AB. Here diameter is always twice the radius of the circle. CD is the secant to the circle and cut the circle at two different points. The tangent PTR touches the circle at one and only one point. Also we have infinite number of tangent on a circle but at a point there will be one and only one tangent that can be drawn. The chord TS in a circle is the line which touches the circle at two different points and diameter is the longest chord.

Properties of a Circle
1. If two chords of a circle are equal, their corresponding arcs have equal measure.
2. Measurement of an arc is the angle subtended at the centre. Equal arcs subtend equal angles at the
center.
3. A line from centre and perpendicular to a chord bisects the chord.
4. Equal chords of a circle are equidistant from the centre.
5. When two circles touch, their centres and their point of contact are collinear.
6. If the two circles touch externally, the distance between their centres is equal to sum of their radii.
7. If the two circles touch internally, the distance between the centres is equal to difference of their radii.

8. Angle at the centre made by an arc is equal to twice the angle made by the arc at any point on the
remaining part of the circumference.
Let O be the centre of the circle.
∠BOC = 2 ∠P, when ∠BAC = ∠P
9. If two chords are equal then the arc containing the chords will also be equal.
10. There can be one and only one circle that touches three non-collinear points.
11. The angle inscribed in a semicircle is 90o.
12. If two chords AB and CD intersect externally or internally at P, then
PA × PB = PC × PD


13. If PAB is a secant and PT is a tangent, then
PT2 = PA × PB

14. The length of the direct common tangent (PQ)


15. The length of the transverse common tangent (RS)


Cyclic Quadrilateral
If a quadrilateral is inscribed in a circle i.e. all the vertex lies on the circumference of the circle, it is said to be cyclic quadrilateral.
1. In a cyclic quadrilateral, opposite angles are supplementary.
2. In a cyclic quadrilateral, if any one side is extended, the exterior angle so formed is equal to the interior opposite angle.
Alternate angle theorem
- Angles in the alternate segments are equal.
- In the given figure, AC is a Chord touching the circle at points A and C. At point A we have a tangent PAT making ∠CAT and ∠CAP with the chord AC. In the circle ∠ABC and ∠ADC are two angles in two different segments.
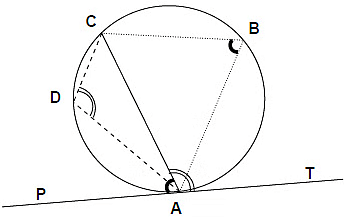
- Here for ∠CAT, the ∠ADC is in alternate segment and for ∠CAP; the ∠ABC is in alternate segment. So according to the statement of the theorem the pair of these alternate angles are equal to each other.
Then, ∠CAT = ∠ ADC &
∠ PAC = ∠ ABC
Example: Find the value of x in the given figure.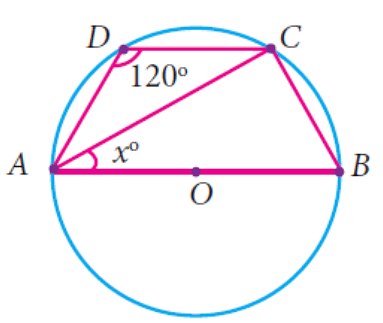
Solution: In triangle ACB,
<ACB = 90° (Angle in a semicircle)
Sum of opposite angles in a quadrilateral = 180°
<ADC + <ABC = 180°
120° + <ABC = 180°
<ABC = 60°
<ACB + <CAB + <ABC = 180°
x + 90° + 60° = 180°
x + 150° = 180°
x = 180° - 150°
x = 30°
|
196 videos|131 docs|110 tests
|
FAQs on Polygons with Solved Examples - Quantitative Aptitude (Quant) - CAT
| 1. What is a cyclic quadrilateral? |  |
| 2. How can you prove that a quadrilateral is cyclic? |  |
| 3. What are the properties of a cyclic quadrilateral? |  |
| 4. How can you calculate the area of a cyclic quadrilateral? |  |
| 5. Can a quadrilateral be cyclic if all its sides are equal in length? |  |

|
Explore Courses for CAT exam
|

|


















