Permutation & Combination | General Aptitude for GATE - Mechanical Engineering PDF Download
| Table of contents |

|
| Introduction |

|
| Fundamental Principle of Counting |

|
| What is Permutation? |

|
| What is Combination? |

|
| Circular Permutations |

|
| MNP Rule |

|
| Important Results |

|
| Solved Examples |

|
Introduction
- Permutation and Combination Questions have always been popular among competitive exams.
- In most competitive exams, questions from permutation and combination are mostly based on the concepts of fundamental principles of counting. There are very rare occasions when the questions on P & C require a higher concept to solve.
- We advise aspirants to stick to the basics and solve permutation and combination questions which require basic concepts and formulas.
Fundamental Principle of Counting
- “If an event can occur in m different ways, following which another event can occur in n different ways, then the total number of occurrences of the events in the given order is m × n.”
- The above principle can be generalized for any finite number of events.
- “If an event can occur in m different ways, following which another event can occur in n different ways, following which a third event can occur in p different ways, then the total number of occurrences to ‘the events in the given order are m × n × p.”
What is Permutation?
- A permutation is defined as an arrangement in a definite order of a number of objects taken, some or all at a time. Counting permutations are merely counting the number of ways in which some or all objects at a time are rearranged. The convenient expression to denote permutation is defined as “ nPr ”.
- The permutation formula is given by:
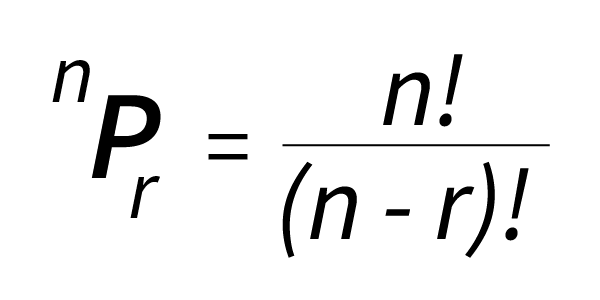
- where the symbol “!” denotes the factorial which means that the product of all the integers is less than or equal to n but it should be greater than or equal to 1.
Factorial Notation:
- The notation n! represents the product of the first n natural numbers, i.e., the product 1 × 2 × 3 × . . . × (n – 1) × n is denoted as n!. We read this symbol as ‘n factorial’.
- Thus, 1 × 2 × 3 × 4 . . . × (n – 1) × n = n !
- For example,
1! = 1
2! = 1 x 2 = 2
3! = 1 x 2 x 3 = 6
4! = 1 x 2 x 3 x 4 = 24, which are the factors of the given number.
Permutation when all the Objects are Distinct
There are some theorems involved in finding the permutations when all the objects are distinct. They are:
- Theorem 1: If the number of permutations of n different objects taken r at a time, it will satisfy the condition 0 < r ≤ n and the objects which do not repeat is n ( n – 1) ( n – 2)……( n – r + 1), then the notation to denote the permutation is given by “ n Pr”
- Theorem 2: The number of permutations of different objects “n” taken r at a time, where repetition is allowed and is given by nr.
Permutation when all the Objects are not Distinct
- Theorem 3: To find the number of permutations of the objects ‘n’, and ‘p’s are of the objects of the same kind and the rest is all different is given as n! / p!
- Theorem 4: The number of permutations of n objects, where p1 are the objects of one kind, p2 are of the second kind, …, pk is of the kth kind and the rest, if any, are of a different kind, then the permutation is given by n! / ( p1!p2!…Pk!)
What is Combination?
- The combination is a selection of a part of a set of objects or a selection of all objects when the order doesn’t matter. Therefore, the number of combinations of n objects taken r at a time.
- The combination formula is given by:
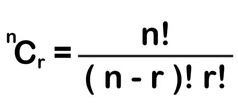 OR
OR
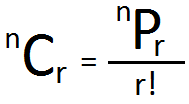
Relationship Between Permutation and combination:
In permutation and combination for class 11, the relationship between the two concepts is given by two theorems. They are:
- Theorem 5: nPr = nCr r! ; if 0 < r ≤ n.
- Theorem 6:nCr + nCr-1 = n+1Cr
Difference between Permutation and Combination
- Permutation involves arranging objects or numbers in a specific order, while combination involves selecting objects or numbers without considering the order.
- In permutation, the order of arrangement matters, whereas in combination, the order of selection does not matter.
- The formula for permutation is nPr = n! / (n - r)!, whereas the formula for combination is nCr = n! / (r! * (n - r)!) (where n is the total number of objects or elements in the set. r is the number of objects or elements to be selected. n! denotes the factorial of n, which is the product of all positive integers from 1 to n).
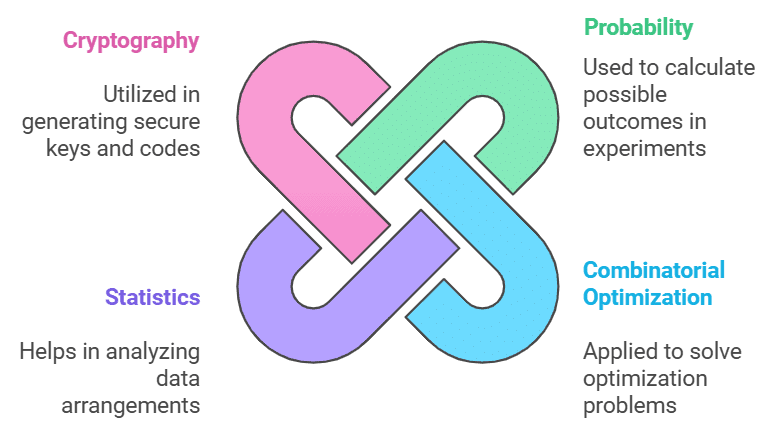
Applications of Permutation and Combination
Permutation and combination have various applications in real-life scenarios and different fields of study. Some common applications include:
Circular Permutations
- Number of circular permutations of n different things taken all at a time = (n −1)!
- Number of circular permutations of n different things taken all at a time in one direction (either clock-wise or anti-clock-wise) = (n-1)!/2
- Number of circular permutations of n different things taken r at a time = nPr/r
- Number of circular permutations of n different things taken r at a time in one direction (either clock-wise or anti-clock-wise) = nPr/2r
MNP Rule
- If there are three tasks to complete.
For the first task, there are M different methods to do it, for the second task there are N different methods to accomplish it and for the third task, there are P different methods available. - The total number of ways to complete all three tasks together is (M x N x P).
- These tasks can be done in any combination, so they are mutually inclusive.
- If the pieces of work are mutually exclusive, then
The total number of ways to complete the work = (M + N + P)
Example: The numbers 1, 2, 3, 4 and 5 are to be used for making three-digit numbers without repetition In how many ways, can this be done?
Sol: Lets visualize it like we have these three places to fill _____ _____ _____
and we have five numbers i.e 1 , 2 , 3 , 4 , 5 to choose from and we have to fill these places taking into consideration that repetition of the numbers is not allowed.
So, there are 5 different ways to fill the first blank (As we have five different numbers to choose from)
Now, As we moved to the second blank, first blank would already have been filled,
So, No. of ways in which 2nd blank can be filled = 4 ways
similarly, No. of ways in which 3rd blank can be filled = 3 ways
now, the total number of ways in which this three digit number can be made out of these 5 numbers is = 5 x 4 x 3 = 60 ways.
Important Results
The following results are very important as this will help you in problem solving



Solved Examples
Example 1: From a pack of cards in how many ways can you select-
a) A king and a queen
b) A king or a queen
Sol: There are 52 cards in a pack, with 4 kings and 4 queens.A king can be selected in 4 ways and a queen can be selected in 4 ways. Number of ways of selection of a king AND a queen is 4×4=16 (Product rule)
Number of ways of selection of a king OR a queen 4+4=8 (Addition rule)
The fundamental principle of counting (FPC) is the basic concept of permutation and combination.
Example 2: In how many ways can 3 people A, B, C be arranged in 2 places?
Sol: Manually solving we will get 6 cases as given below.AB BA
AC CA
BC CB
This can be explained using FPC like this
There are two seats __ __.
In the first seat A,B or C can sit. i.e., 3 possibilities.Let A sit in the first place. Thus, in second place either B or C can sit.
The second seat can hence be taken up in 2 ways Together A,B ‘AND’ C can be seated in 3 x 2 = 6 ways.
Thus, the number of arrangement of 3 things at 2 places can be done in 3×2 ways.
Example 3: In how many ways can 4 people be seated in 3 chairs?
Sol:
- First seat can be filled in 4 ways
- Second seat can be filled in 3 ways.
- Third seat can be filled in 2 ways.
- So all together 4 people can be arranged in 3 seats in 4x3x2 = 24 ways.
Sol:
- Choose the President: There are 3 choices.
- Choose the Vice-President: After choosing the President, there are 2 remaining choices= 3 × 2 = 6
There are 6 ways to select a President and a Vice-President from 3 people.
Example 5: a, b, c are three distinct integers from 2 to 10 (both inclusive). Exactly one of ab, bc and ca is odd. abc is a multiple of 4. The arithmetic mean of a and b is an integer and so is the arithmetic mean of a, b and c. How many such triplets are possible (unordered triplets)?
Sol:
- Exactly one of ab, bc and ca is odd
- Two are odd and one is even.
- abc is a multiple of 4
- Which means the even number is a multiple of 4.
- The arithmetic mean of a and b is an integer implies a and b are odd.
and so is the arithmetic mean of a, b and c.- hence, a + b + c is a multiple of 3.
c can be 4 or 8.- c = 4; a, b can be 3, 5 or 5, 9
- c = 8; a, b can be 3, 7 or 7, 9
- Four triplets are possible.
- Hence the correct answer is 4.
Example 6: If we listed all numbers from 100 to 10,000, how many times would the digit 3 be printed?
Sol:
- 3-Digit Numbers (100 to 999):
- Hundreds place (300-399): 100 times
- Tens place (130-139, 230-239, ..., 930-939): 90 times
- Units place (103, 113, ..., 993): 90 times
- Total for 3-digit numbers:
- 4-Digit Numbers (1,000 to 9,999):
- Thousands place (3000-3999): 1000 times
- Hundreds place (1300-1399, ..., 9300-9399): 900 times
- Tens place (x30, x31, ..., x39 for each thousand): 900 times
- Units place (x03, x13, ..., x93 for each thousand): 900 times
- Total for 4-digit numbers:
1000+ 900 + 900 + 900 = 3700
Total occurrences of '3' from 100 to 9,999:
Example 7: All numbers from 1 to 150 (in decimal system) are written in base 6 notation. How many of these will contain zero's?
Sol:
- Any multiple of 6 will end in a zero. There are 25 such numbers.
- Beyond this, we can have zero as the middle digit of a 3-digit number.
- This will be the case for numbers from 37 - 41, 73 - 77, 109 - 113, and 145 - 149. There are 20 such numbers.
- Overall, there are 45 numbers that have a zero in them.
- Hence the correct answer is 45.
|
229 videos|191 docs|158 tests
|
FAQs on Permutation & Combination - General Aptitude for GATE - Mechanical Engineering
| 1. What is the difference between permutation and combination? |  |
| 2. How do you calculate the number of permutations of 'n' items taken 'r' at a time? |  |
| 3. What is the formula for combinations and how is it different from permutations? |  |
| 4. Can you explain circular permutations and how they differ from linear permutations? |  |
| 5. What is the MNP rule in permutations and combinations? |  |
















