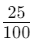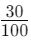Decimals Class 6 Notes Maths Chapter 8
| Table of contents |

|
| Introduction |

|
| Comparing Decimals |

|
| Using Decimals |

|
| Addition of Numbers with Decimals |

|
| Subtraction of Decimals |

|
Introduction
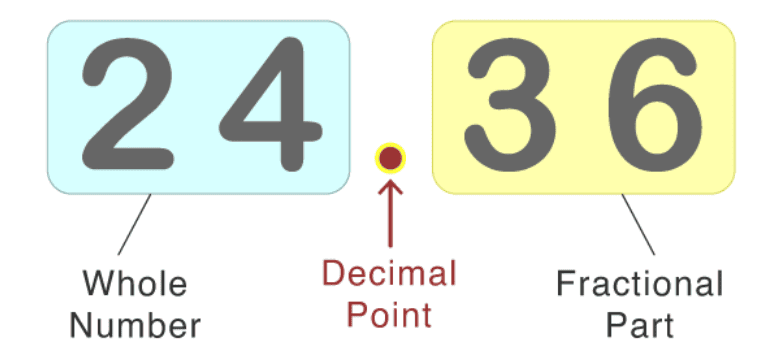
Decimals are an essential part of mathematics that help us represent numbers that are not whole. They are used in everyday life for things like money, measurements, and data analysis. A decimal number has two parts: a whole number and a fractional part, separated by a decimal point.
Example:
If you have 1 rupee and 50 paise, you can write it as ₹1.50. Here, 1 is the whole number (rupee), and 50 is the part of the rupee (paise) that comes after the decimal point. The dot represents the decimal point and is positioned between the units place and the tenths place. Therefore, ₹1.50 means 1 rupee and 50 paise.
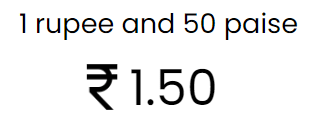
Comparing Decimals
Let us first understand the basics before we start comparing decimals.
(i) Converting Fractions to Decimals: To convert a fraction to a decimal, make the denominator 10, 100, etc.
Example: Convert 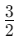 to a decimal
to a decimal
Multiply both the numerator and denominator by 5 to make the denominator 10:
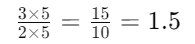
So, 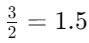 in decimal form.
in decimal form.
(ii) Converting Decimals to Fractions: To convert a decimal to a fraction, place the decimal number over 10, 100, etc., depending on the number of digits after the decimal point.
Example: Convert 8.9 to a fraction
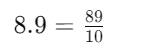
(iii) Any two decimal numbers can be compared by comparing their whole part and decimal parts.
Let us understand this by comparing 0.07 and 0.1
- Imagine you have two square pieces of paper, both divided into 100 equal parts.
For 0.07: Shade 7 out of the 100 parts.
For 0.1: Shade 10 out of the 100 parts.
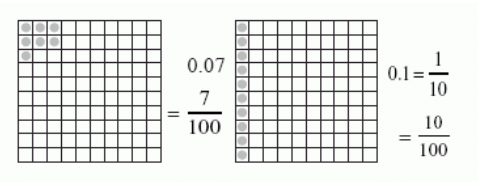
- 0.07 means 7 parts out of 100, which can be written as
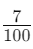
- 0.1 means 1 part out of 10, which can also be written as
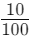 (since 1 out of 10 is the same as 10 out of 100).
(since 1 out of 10 is the same as 10 out of 100). - Since 10 parts out of 100 is more than 7 parts out of 100, 0.1 is greater than 0.07.
Example: Which is greater: 0.3 or 0.25?
Ans: Let us solve this by imagining you have two chocolate bars, both divided into 100 equal pieces.
First bar (0.25):
- You have 25 pieces out of 100.
- This represents
Second bar (0.3):
- You have 30 pieces out of 100.
- This represents
Since 30 pieces are more than 25 pieces, 0.3 is greater than 0.25.
(iv) Comparing Decimals with the Same Whole Number
Let's compare two numbers: 45.78 and 45.7. Here's how to do it step by step:
- 45.78 can be written as
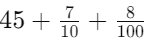
- 45.7 can be written as
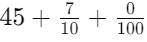
Since the whole part (45) and the tenths place (7) are equal, we move to the hundredths place:
45.78 has 8 in the hundredths place.
45.7 has 0 in the hundredths place (or 45.70).
Therefore, 45.78 > 45.7 because the hundredths part of 45.78 is more.
Even if the whole and tenth parts of two numbers are the same, you must compare the next digit (hundredth place) to find out which number is greater. In this example, 45.67 is greater because it has a larger hundredths value than 45.6.
Example: Compare 64.24 and 64.205
Ans:Compare the whole number parts:
Both 64.24 and 64.205 have the same whole number part: 64.Compare the decimal parts digit by digit:
First decimal place:
64.24 has 2, and 64.20564.205 also has 22. (Equal)
Second decimal place:
64.24 has 44, and 64.20564.205 has 0.
Since 4>0, 64.24>64.205.
Using Decimals
Money
Working with decimal numbers is essential when handling money, especially in cases where we need to convert paisa into rupees.

100 paise = ₹1
Therefore, 1 paise = ₹0.01 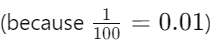
If we have to convert 5 paise to rupees, divide by 100.
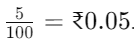
For example, if we visit a local shop to purchase 500 grams of turmeric, and 1 kg of turmeric costs Rs. 51, we need to determine how much to pay the shopkeeper. By dividing Rs. 51 by 2, we get Rs. 25.5. To pay the correct amount, we need to understand what Rs. 25.5 represents in rupees. Let's explore this through a simple example.
Rs 1 = 100 paisa
Rs 0.5 = 50 paisa
Rs. 25.5 = Rs. 25 and 50 paisa
Q1: Convert 165 paisa to rupees.
Ans: Since 1 paisa = Rs. 1/100,
165 paisa = Rs. 165 × (1/100) = Rs. 165/100 = Rs. 1.65, which equals
Rs. 1 and 65 paisa.
Q2: Convert 350
Ans: Since 1 paisa = Rs. 1/100,
350 paisa = Rs. 350 × (1/100) = Rs. 350/100 = Rs. 3.50, which equals
Rs. 3 and 50 paisa.
Length
When measuring the length of an item, it's not always the case that the length will be a multiple of the scale's markings.
For example, when using a meter scale to measure the length of a table, the measurement might not be a whole number and could fall between two markings on the scale. In such cases, decimal numbers are used.
From unit conversion, we know:
- 1 km = 1000 m
- 1 m = 100 cm
- 1 cm = 10 mm
If the length of the tabletop is 2 meters and 75 centimeters, it can be represented as (2 + 75/100) meters.
Q1: Convert 5 km and 75 m into decimal.
Ans: As we know, 1 km = 1000 m
So, 1 m = 1/1000 km
5 km + 75 m = 5 + (75 × 1/1000) km = 5.075 km
Q2: Convert 61km and 25m into decimal.
Ans:
Convert meters to kilometers:
- Since 1 kilometer = 1000 meters, 25 meters is kilometers.
- =0.025 km
Add the kilometers:
- 61 kilometers + 0.025 kilometers = 61.025 kilometers.
Weight
Decimal numbers are commonly used when dealing with weight.

For example, when you buy a watermelon, its weight may not be a whole number; it could be more than 1 kg but less than 2 kg. In these cases, the shopkeeper needs to calculate the price based on the precise weight of the watermelon. We know that:
- 1 kg = 1000 g
- 1 g = 1000 mg
If the watermelon weighs 1 kg and 750 g, the shopkeeper will charge for 1 kg plus (750/1000) kg of watermelon. Let's look at converting weight into decimals through the following example:
Q1: Convert 250 g to kg.
Ans: Since 1000 g = 1 kg,
1 g = 1/1000 kg,
250 g = 250 × (1/1000) kg = 250/1000 kg = 0.250 kg.
We know that 1 g = kg.
So, 396 g = kg.
Therefore, 5 kg + 0.396 kg = 5.396 kg.
Addition of Numbers with Decimals
Steps for Addition of Numbers with Decimals:
- Line Up the Decimals: Place the numbers one below the other, making sure the decimal points are aligned. If any number is shorter, add zeros to make the lengths equal.
- Add the Numbers: Add the numbers as you would with whole numbers, starting from the rightmost digit.
- Place the Decimal Point: In the final answer, put the decimal point directly below the other decimal points in the same column.
Example: Add 0.56 + 9 + 6.287
To add decimals, line up the decimal points vertically and fill in 0's as shown:

Q1: The total weight of a box containing 14kg750g of mangoes, 5kg 80g of apples is 22kg 200g. How much is the weight of the empty box?
Ans: Weight of mangoes =14kg750g
Weight of Apples =5kg80g
Total weight of box =22kg200g

So, the weight of empty box = total box weight - total weight of fruits
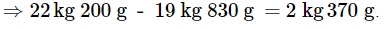
Q2: Add 27.076 + 0.55 + 0.004
Ans: 27.076 + 0.55 + 0.004
It can be written as 27.076 + 0.550 + 0.004 = 27.630
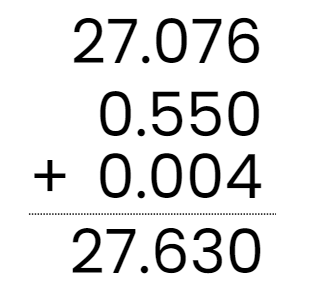
Q3: Nasreen bought 3 m 20 cm cloth for her shirt and 2 m 5 cm cloth for skirt. Find the total cloth bought by her.
Ans: Cloth bought by Nasreen for shirt = 3 m 20 cm = 3.20 m
Cloth bought by Nasreen for skirt = 2 m 50 cm = 2.05 m
So the total cloth bought by her = 3.20 + 2.05 = 5.25 m = 5 m 25 cm
Hence, the total cloth bought by her is 5 m 25 cm.
⇒22kg 200 g - 19 kg 830 g = 2k
Subtraction of Decimals
Steps for Subtraction of Numbers with Decimals:
- Line Up the Decimals: Arrange the numbers in a vertical format, making sure the decimal points are directly under each other. Add zeros if needed to equalize the lengths.
- Subtract the Numbers: Subtract the numbers as you would with whole numbers, beginning from the rightmost digit.
- Place the Decimal Point: In the final difference, position the decimal point directly below the aligned decimal points.
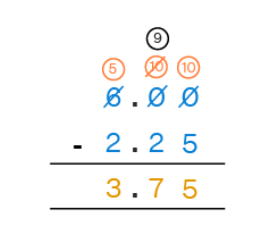
Example: Subtract 6 – 2.25
To subtract decimals, line up the decimal points vertically and add 0's where shown. Remember to borrow when necessary.
Q1: Ganesh purchased a book worth Rs.156.65 from a bookseller and he gave him Rs.500 note. How much balance did he get back?
Ans: Cost of book = Rs. 156.65
Total amount given by Ganesh = Rs. 500
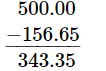
Q2: Subtract 27.56 from 52.1
Ans: By subtracting 27.56 from 52.1
52.10−27.56=24.54
Therefore, we get 24.54 on subtracting 25.76 from 52.1
|
30 videos|120 docs|59 tests
|
FAQs on Decimals Class 6 Notes Maths Chapter 8
| 1. What are decimals and how are they used in everyday life? |  |
| 2. How do you compare two decimal numbers? |  |
| 3. How do you add numbers with decimals? |  |
| 4. What is the process for subtracting decimals? |  |
| 5. Why is it important to understand decimals in mathematics? |  |