Important Logarithms Formulas for JEE and NEET
| Table of contents |

|
| What are Logarithms? |

|
| Logarithm |

|
| Types of Logarithms |

|
| Logarithm Properties |

|
| Characteristics and Mantissa |

|
| Important Conversions |

|
| Logarithm Rules |

|
| Solved Examples |

|
What are Logarithms?
A logarithm is defined as the power to which a number must be raised to get some other values. It is the most convenient way to express large numbers. A logarithm has various important properties that prove multiplication and division of logarithms can also be written in the form of a logarithm of addition and subtraction.
“The logarithm of a positive real number a with respect to base b, a positive real number not equal to 1[nb 1], is the exponent by which b must be raised to yield a”.
i.e. by= a ⇔logba=y
Where,
- “a” and “b” are two positive real numbers
- y is a real number
- “a” is called argument, which is inside the log
- “b” is called the base, which is at the bottom of the log.
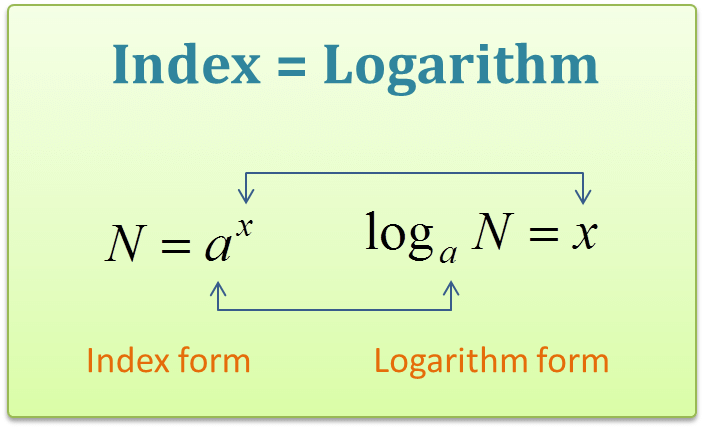
In other words, the logarithm gives the answer to the question “How many times a number is multiplied to get the other number?”.
For example, how many 3’s are multiplied to get the answer 27?
If we multiply 3 for 3 times, we get the answer 27.
Therefore, the logarithm is 3.
The logarithm form is written as follows:
Log3 (27) = 3 ….(1)
Therefore, the base 3 logarithm of 27 is 3.
The above logarithm form can also be written as:
3 x 3 x 3 = 27
33 = 27 …..(2)
Thus, the equations (1) and (2) both represent the same meaning.
Below are some of the examples of conversion from exponential forms to logarithms.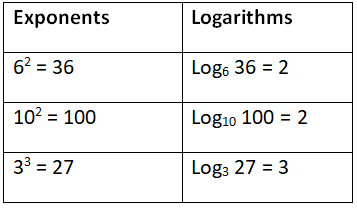
Logarithm
Let a,b be positive real numbers
So, ax =b can be written as
loga b = x a ≠1≠1, a > 0, b > 0
Ex:- 35 = 243 ⇔⇔ log3 243 = 5
Types of Logarithms
(i) Natural Logarithm: loge N is called natural Logarithm or Naperian Logarithm denoted by (ln N) i.e., when logarithm’s base is “e” then it is called natural logarithm. Ex: loge 7
(ii) Common Logarithm: log10 N is called Brigg’s Logarithm when the base is 10. Ex: log10 100
Logarithm Properties
- loga 1 = 0, a > 0, a ≠ 1
- loga a = 1, a > 0, a ≠ 1
- Loga ax = x, x ∀ x ∈ R, x >0
- aloga x = x, x ∀ x ∈ R, x >0
- loga (m.n) = loga m + loga n, n ∀ m, n > 0, a > 0, a ≠ 1
- loga (m/n) = loga m – loga n, n ∀ m, n > 0, a > 0, a ≠ 1
- loga (mn) = n loga m, m ∀ m, m > 0, a > 0, a ≠ 1
- loga (1/m) = – loga m, m ∀ m, n > 0, a > 0, a ≠ 1
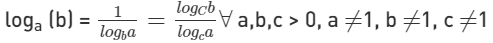
- loga b = x ∀ a, b > 0, a ≠ 1 and x ∈ R
(i) log1/a b = – x
(ii) loga (1/b) = – x
(iii) log1/a (1/b) = -x - logam b = 1/m loga b
- loga x is a decreasing function, if 0 < a < 1
- loga x is a increasing function, if a > 1
- When 0 < a < 1 then
- loga b ≥ loga c, ⇔ b ≤ c
- loga b ≥ c, ⇔ b ≤ ac
- When a >1
- loga b ≥ loga c, ⇔ b ≥ c > 0
- loga b ≥ c, ⇔ b ≥ ac
Characteristics and Mantissa
Characteristic: The integral part of logarithm is known as characteristic.
Mantissa: The decimal part is known as mantissa and is always positive
 In log 3274 = 3.5150, the integral part is 3 i.e., characteristic is 3 and the decimal part is .5150 i.e., mantissa is .5150.
In log 3274 = 3.5150, the integral part is 3 i.e., characteristic is 3 and the decimal part is .5150 i.e., mantissa is .5150.
Points to Remember About Characteristics
- The characteristic of common logarithm of positive number less than unity (i.e.,1) is negative.
- The characteristic of common logarithm of a positive number greater than 1 is positive.
- If the logarithm to any base a gives the characteristic ‘n’, then the number of possible integral values is given by an+1 −an. For example log10 x = n.abcd, then the number of integral values that x can have given by 10n+1 −10n
- If the characteristic of log10 x is negative (i.e., − n), then the number of zeros between the decimal and the first significant number after the decimal is (n −1)
Important Conversions
- For a > 1, a 1, c > 0, a b > c ⇔ loga c < b
- For 0 < a < 1, a 1, c > 0, a b > c ⇔ loga c > b
Logarithm Rules

There are certain rules based on which logarithmic operations can be performed. The names of these rules are:
- Product rule
- Division rule
- Power rule/Exponential Rule
- Change of base rule
- Base switch rule
- Derivative of log
- Integral of log
Let us have a look at each of these properties one by one
1. Product Rule
In this rule, the multiplication of two logarithmic values is equal to the addition of their individual logarithms.
Logb (mn)= logb m + logb n
Example: log3 ( 2y ) = log3 (2) + log3 (y)
2. Division Rule
The division of two logarithmic values is equal to the difference of each logarithm.
Logb (m/n)= logb m – logb n
Example: log3 (2/ y) = log3 (2) -log3 (y)
3. Exponential Rule
In the exponential rule, the logarithm of m with a rational exponent is equal to the exponent times its logarithm.
Logb (mn) = n logb m
Example: logb(23) = 3 logb 2
4. Change of Base Rule
Logb m = loga m/ loga b
Example: logb 2 = loga 2/loga b
5. Base Switch Rule
logb (a) = 1 / loga (b)
Example: logb 8 = 1/log8 b
6. Derivative of log
If f (x) = logb (x), then the derivative of f(x) is given by;
f'(x) = 1/(x ln(b))
Example: Given, f (x) = log10 (x)
Then, f'(x) = 1/(x ln(10))
7. Integral of Log
∫logb(x)dx = x(logb(x) – 1/ln(b)) + C
Example: ∫ log10(x) dx = x ∙ (log10(x) – 1 / ln(10)) + C
Always remember:
- logb(mn) = logb(m) + logb(n)
- logb(m/n) = logb (m) – logb (n)
- Logb (xy) = y logb(x)
- Logbm√n = logb n/m
- m logb(x) + n logb(y) = logb(xmyn)
- logb(m+n) = logb m + logb(1+nm)
- logb(m – n) = logb m + logb (1-n/m)
Solved Examples
Question 1: If log2X + log4X = log0.25√6 and x > 0, then x is:
A. 6-1/6
B. 61/6
C. 3-1/3
D. 61/3
Correct Answer is Option (A).
- log2x + log4x = log0.25√6
We can rewrite the equation as: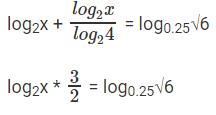
⇒ log2x * 3 = 2log0.25√6
⇒ log2x3 = -log46
⇒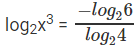
⇒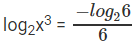
⇒ 2log2x3 = -log26 - 2log2x3 + log26 = 0
log26X6 = 0 - 6x6 = 1
x6 = 1/6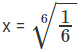
- The question is "If log2X + log4X = log0.25 √6 and x > 0, then x is"
- Hence, the answer is "6-1/6".
Question 2: log9 (3log2 (1 + log3 (1 + 2log2x))) = 1/2. Find x.
A. 4
B. 1/2
C. 1
D. 2
Correct Answer is Option (D).
log9 (3log2 (1 + log3 (1 + 2log2x)) = 1/2
3log2(1 + log3(1 + 2log2x)) = 91/2 = 3
log2(1 + log3(1 + 2log2x) = 1
1 + log3(1 + 2log2x) = 2
log3(1 + 2log2x) = 1
1 + 2log2x = 3
2log2x = 2
log2x = 1
x = 2
The question is "Find x."
Hence, the answer is "2".
Question 3: If 22x+4 – 17 × 2x+1 = –4, then which of the following is true?
A. x is a positive value
B. x is a negative value
C. x can be either a positive value or a negative value
D. None of these
Correct Answer is Option (C).
2x+4 – 17 * 2x+1 = – 4
=> 2x+1 = y
22x+2 = y2
22(22x+2) – 17 * 2x+1 = –4
4y2 – 17y + 4 = 0
4y2 – 16y – y + y = 0
4y (y – 4) – 1 (y – 4) = 0
y = 1/4 or 4
2x+1 = 1/4 or 4
⇒ x + 1 = 2 or – 2
x = 1 or – 3
The question is "which of the following is true?"
Hence, the answer is "x can be either a positive value or a negative value".
Question 4: If log1227 = a, log916 = b, find log8108
A. 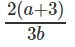
B. 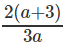
C. 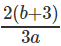
D. 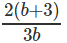
Correct Answer is Option (D).
log8108 = log8(4 * 27)
log8108 = log84 + log827
⇒ log84 = 2/3
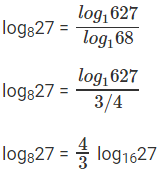
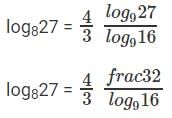
log827 = 2 * log169
log916 = b
log169 = 1/b
log827 = 2/b
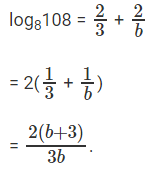
The question is "find log8108."
Hence, the answer is 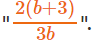
Question 5: 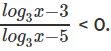 If a, b are integers such that x = a, and x = b satisfy this inequation, find the maximum possible value of a – b.
If a, b are integers such that x = a, and x = b satisfy this inequation, find the maximum possible value of a – b.
A. 214
B. 216
C. 200
D. 203
Correct Answer is Option (A).
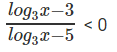
log3x = y
⇒ 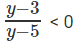
y ∈ (3, 5)
3 < log3x < 5
27 < x < 243
Therefore max ( a – b) will be when a = 242 and b = 28. Therefore, max(a – b) = 214.
The question is "find the maximum possible value of a – b."
Hence, the answer is "214".
Question 6: log5x = a (This should be read as log X to the base 5 equals a) log20x = b. What is logx10?
A. 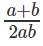
B. (a + b) * 2ab
C. 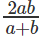
D. 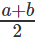
Correct Answer is Option (A).
Given, log5x = a
log20x = b
logx5 = 1/a
logx20 = 1/b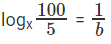
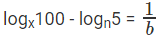
⇒ 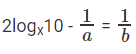
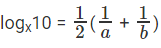
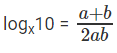
The question is "What is logx10?"
Hence, the answer is 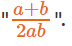
Question 7: log3x + logx3 = 17/4. Find x.
A. 34
B. 31/8
C. 31/4
D. 31/3
Correct Answer is Option (C).
log3x + logx3 = 17/4
Let y = log3x
We know that logx3 = 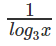
Hence logx3 = 1/y
Thus the equation can be written as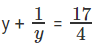
4y2 + 4 = 17y
4y2 + 4 - 17y = 0
Solving the above equation we get y = 4 or 1/4
If y = 4
log3x = 4
Then x = 34
If y = 1/4
log3x = 1/4
Then x = 31/4
The question is "Find x."
Hence, the answer is "34".
Question 8: logxy + logyx2 = 3. Find logxy3.
A. 4
B. 3
C. 31/2
D. 31/16
Correct Answer is Option (B).
logxy + logyx2 = 3
Let a = logxy
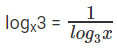
logyx2 = 2logyx
We know that logyx =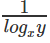
Hence form above logyx = 1/a
Now rewritting the equation logxy + logyx2 = 3
Using a we get 
i.e., a2 - 3a + 2 = 0
Solving we get a = 2 or 1
If a = 2, Then logxy = 2 and logyx3 = 3
logxy = 3 * 2 = 6
Or
If a = 1, Then logxy = 1 and logyx3 = 3
logxy = 3 * 1 = 3
The question is "Find logxy3."
Hence, the answer is "3".
Question 9: log2 4 * log4 8 * log8 16 * ……………nth term = 49, what is the value of n?
A. 49
B. 48
C. 34
D. 24
Correct Answer is Option (B).
First, the nth term of L.H.S need to be defined by observing the pattern :-
It is log(2n) 2.2n
Given,
log2 4 * log4 8 * log8 16 * ……………log(2n) 2.2n = 49
Whenever solving a logarithm equation, generally one should approach towards making the base same.
Making the base 2:-
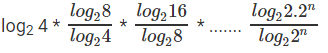
log(2n) 2.2n = 49
log(2n) 2 + log(2n) 2n = 49
1 + n = 49
n = 48
The question is "what is the value of n?"
Hence, the answer is "48".
Question 10: If 33 + 6 + 9 + ……… 3x =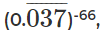 what is the value of x?
what is the value of x?
A. 3
B. 6
C. 7
D. 11
Correct Answer is Option (D).
First of all, let us define the xth term.

Whenever you encounter a distinctive number such as one given in R.H.S of above equation, always try to find its significance in the context of question.
In this case L.H.S has 3a, so 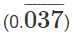 must be some form of 3a.
must be some form of 3a.
With little hit and trial, you may find 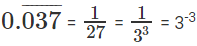
33(1 + 2 + 3 + ...X) = 3 -3 * -66
⇒ 33 * 3x(x+1)/2 = 33*66
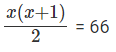
x(x+1) = 132
Solving this equation for x > 0, we get x = 11.
You should directly be able to see that 132 = 11 * 12 => x= 11
And avoid wasting time solving the complete equation.
The question is "what is the value of x?"
Hence, the answer is "11".
Question 11: x, y, z are 3 integers in a geometric sequence such that y - x is a perfect cube. Given, log36x2 + log6√y + log216y1/2z = 6. Find the value of x + y + z.
A. 189
B. 190
C. 199
D. 201
Correct Answer is Option (A).
Let us begin with simplifying the equation:-
⇒ log62x2 + log6y1/2 + 3log63y1/2z = 6

log6x + log6y1/2y1/2z = 6
log6xyz = 6
xyz = 66
Given x,y,z is in G.P. Let x = a, y = ab, z = ab2
⇒ xyz = a3b3 = (ab)3
(ab)3 = (62)3
Possible values of (a,b) satisfying the equation :-
(1, 36), (2, 18), (3, 12), (4, 9), (9, 4), (12, 3), (18, 2), (36, 1)
Given y-x is a perfect cube
⇒ ab-a is perfect cube
⇒ a(b-1) is perfect cube
Only possible when (a, b) = (9, 4)
∴ x = 9 , y = 36 , z = 144
∴ x + y + z = 9 + 36 + 144 = 189
The question is "Find the value of x + y + z."
Hence, the answer is "189".
Question 12: 10log(3 - 10logy) = log2(9 - 2y), Solve for y.
A. 0
B. 3
C. 0 and 3
D. none of these
Correct Answer is Option (D).
Before beginning to simplify the equation, don’t forget that anything inside a log cannot be negative
10log(3-y) = log2(9 - 2y) (y > 0)…………………………………(1)
3 - y = log2(9 - 2y) (Therefore, 3 - y > 0 =) (y < 3)) ……………………… (2)
23-y = 9 - 2y
2y = t
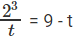
⇒ 8 = 9t –t2
⇒ t2 - 9t + 8 = 0
⇒ t2 - t - 8t - 8 = 0
⇒ t(t - 1) - 8(t - 1) = 0
⇒ t = 1, 8
Therefore, 2y = 1 and 2y = 8
⇒ y = 0 and y = 3
However, from inequalities (1) and (2), y cannot take either of these value.
The question is "Solve for y."
Hence, the answer is "none of these".
Question 13: 46+12+18+24+…+6x = (0.0625)-84, what is the value of x?
A. 7
B. 6
C. 9
D. 12
Correct Answer is Option (A).
Take right side expression,
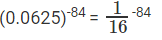
= (4-2)-84
= 4168
Take left side expression
46+12+18+24+…+6x = 46(1+2+3+4+x)
= 46 * 4(1+2+3+4+…+x)
= 46 * 4x(x+1)/2 (using the formula for sum of natural numbers from 1 to x)
Equating left and right side expresssions, we get 46 * 4x(x+1)/2 = 4168
Or 46 * 4x(x+1)/2 = 46*28
⇒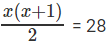
or x (x + 1) = 56
Solving for x we get, x = 7
The question is "what is the value of x?"
Hence, the answer is "7".
|
205 videos|264 docs|136 tests
|
FAQs on Important Logarithms Formulas for JEE and NEET
| 1. What are the different types of logarithms? |  |
| 2. What are some important logarithm rules to remember? |  |
| 3. What are some key logarithm properties to be aware of? |  |
| 4. What are characteristics and mantissa in logarithms? |  |
| 5. How can logarithms be used for important conversions and calculations? |  |
















