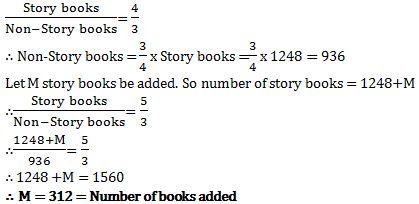Important Formulas: Ratio and Proportion | General Test Preparation for CUET UG - CUET Commerce PDF Download
Ratio and Proportion are essential tools for solving a wide range of quantitative problems. They help compare quantities, determine relationships, and simplify calculations in topics like percentages, mixtures, time-speed-distance, and geometry. A clear understanding of these concepts improves accuracy and speeds up problem-solving across multiple areas of mathematics.

Introduction
- Ratio and Proportion are explained mainly based on fractions.
- Ratio is the comparison of two similar quantities using division and is represented as a : b or a/b.
- Proportion is an equation that states two ratios are equal: a : b = c : d or a : b :: c : d.

What is a Ratio?
- A ratio compares two quantities of the same kind.
- It is an abstract quantity and has no units.
- In a : b,
a is the antecedent
b is the consequent.

Example 1: The ratio 5 : 9 represents 5/9 with antecedent = 5, consequent = 9.
Example 2: If we multiply and divide each term of a ratio by the same number (non-zero), it doesn’t affect the ratio
like 5:9 = 10:18 = 15:27
Important Properties of Ratio
1. A ratio remains the same if both antecedent and consequent are multiplied or divided by the same non-zero number,
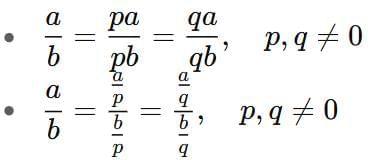
2. Two ratios in their fraction notation can be compared just as we compare real numbers.
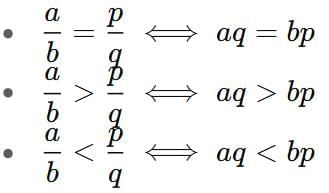
3. If two ratios a/b and c/d are equal

Key Points to Remember about Ratio:
- The ratio should exist between the quantities of the same kind.
- While comparing two things, the units should be similar.
- There should be significant order of terms.
- The comparison of two ratios can be performed, if the ratios are equivalent like the fractions.
Types of Ratios
1. Compounded Ratio:
- The compounded ratio of the ratios (a : b), (c : d), (e : f) is (ace : bdf)
2. Duplicate Ratios
- The duplicate ratio of (a : b) is (a2 : b2)
- Sub - duplicate ratio of (a : b) is (√a : √b)
- Triplicate ratio of (a : b) is (a3 : b3)
- Sub - triplicate ratio of (a : b) is (a1/3: b1/3)
- Componendo and Dividendo Rule
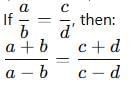
What is a Proportion?
The equality of two ratios is called proportion i.e. If a/b = c/d, then a, b, c, d are said to be in proportion.
- If a: b = c : d, we write a: b:: c : d and saying that a, b, c, d are in proportion.
- Here a and d are called Extremes, while b and c are called Mean terms.
Product of means = Product of extremes
Thus, a : b :: c : d ⇔ (b x c) = (a x d)
Important Properties of Proportion
If a:b = c:d is a proportion, then
1. Product of extremes = product of means
=> ad = bc
2. Continued Proportion:
a : b = b : c = c : d
3. Mean Proportional:
If a : b = b : c, then b² = a × c
4. Third Proportional:
If a : b = b : c, then c is the third proportional.
5. Fourth Proportional:
If a : b = c : d, then d is the fourth proportional.
6. Variations
- We define that a is directly proportional to b, if a=kb for some constant k and we write it as – a is proportional to b.
- We say that a is indirectly proportional to b, if ay=b for some constant k and we write it as – a is proportional to 1/b.
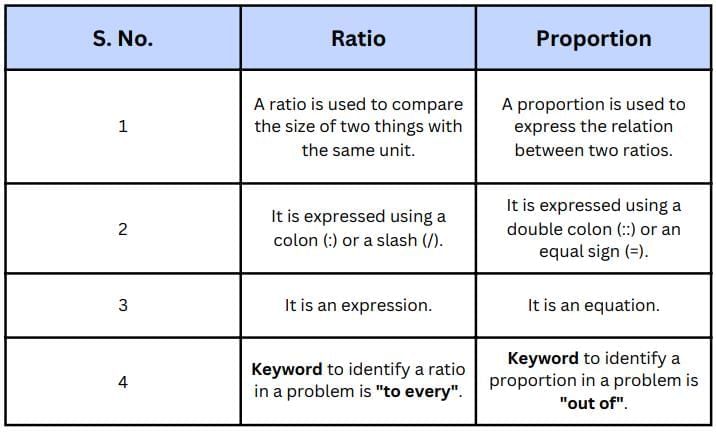
Difference Between Ratio and Proportion
To understand the concept of ratio and proportion, go through the difference between ratio and proportion given here.
Simple Method to Solve Ratio & Proportion Questions
The LCM process gets very cumbersome when we have to find the ratio out of multiple ratios.
We have the following simple method for that for a chain of ratios of any length.
Suppose you have the ratio train as follows
⇨ A : B = 1 : 2
⇨ B : C = 2 : 3
⇨ C : D = 5 : 6
⇨ D : E = 7 : 8
If we were to find A : B : C : D : E, then the LCM method would have taken quite a long time which is infeasible in examinations of limited hours.
The short cut is as follows:
A : B : C : D : E can be written directly as:
⇨ 1 × 2 × 5 × 7 : 2 × 2 × 5 × 7 : 2 × 3 × 5 × 7 : 2 × 3 × 6 × 7 : 2 × 3 × 6 × 8
⇨ 70 : 140 : 210 : 252 : 288
The thought algorithm for this case goes as:
To get the combined ratio of A : B : C : D : E, from A : B, B : C, C : D, and D : E
In the combined ratio of A : B : C : D : E.
- A will correspond to the product of all numerators (1 × 2 × 5 × 7).
- B will take the first denominator and the last 3 numerators (2 × 2 × 5 × 7).
- C, on the other hand, takes the first two denominators and the last 2 numerators (2 × 3 × 5 × 7).
- D takes the first 3 denominators and the last numerator (2 × 3 × 6 × 7) and E take all the four denominators (2 × 3 × 6 × 8).
Ratio and Proportion Tricks
1. 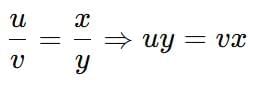
2. 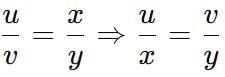
3. 
4. 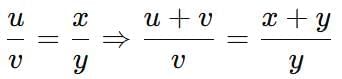
5. 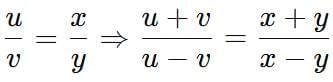
6. 
Solved Questions
Q1: In a library, the ratio of the number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.
Ans: Option A
Explanation:
Q2: Rs. 8400 is divided among A, B, C and D in such a way that the shares of A and B, B and C, and C and D are in the ratios of 2:3, 4:5, and 6:7 respectively. The share of A is
Ans: Option A
Explanation:
Q3: The ratio of the present age of father to that of son is 7:2. After 10 years their ages will be in the ratio of 9:4. The present ages of the father is
Ans: Option A
Explanation:
The given ratio of the father's age to the son's age is 7 : 2.
This means the father's age must be divisible by 7.
Among the given options, only 35 is divisible by 7.
Alternative MethodLet the common factor be K
So,Father's present age = 7K
Son's present age = 2K
After 10 years:
Father's age = 7K + 10
Son's age = 2K + 10
Given:
(7K + 10) / (2K + 10) = 9 / 4
Cross-multiplying:
4 × (7K + 10) = 9 × (2K + 10)
28K + 40 = 18K + 90
Solving:
28K - 18K = 90 - 40
10K = 50
K = 5
Therefore, Father's present age = 7K = 7 × 5 = 35 years
Q4: Ajay and Raj together have Rs. 1050. On taking Rs. 150 from Ajay, Ajay will have same amount as what Raj had earlier. Find the ratio of amounts with Ajay and Raj initially.
Ans: Option D
Explanation:

Q5: Price of each article of type P, Q, and R is Rs. 300, Rs. 180 and Rs. 120 respectively. Suresh buys articles of each type in the ratio 3:2:3 in Rs. 6480. How many articles of type Q did he purchase?
a. 8
Ans: Option A
Explanation:
Q6: Divide Rs. 60 in the ratio 1:2 between Mike and John.
Sol: Let Mike’s part be x.
Then John’s part is 2x.
Thus, x+2x = 60
3x = 60
x = (60/3)
x = 20.
Therefore, Mike’s part = x = Rs. 20
John’s part = 3x = Rs. (2*20) = Rs. 40
Q7: Three Jars contain alcohol to water in the ratios 3:5, 1:3, and 1:1. If all the three solutions are mixed, what will be the ratio of alcohol to water in final solution?
Sol: Here we are not given the quantities of the solution in three jars. Only the ratio of alcohol to water is given. If the ratio of the quantity of solution would have been there, we could determine the ratio of alcohol to water in the final solution. Hence, the answer here will be cannot be determined.
Q8: If there are Rs. 495 in a bag in denominations of one-rupee, 50-paisa, and 25-paisa coins which are in the ratio 1:8:16. How many 50 paisa coins are there in bag?
Sol: Assume, you have x numbers of one rupee coin. Now coins are in the ratio 1:8:16. This means that if we have x number of one rupee coins, we have 8x number of 50 paisa coins and 16x number of 25 paisa coins. Here order in which ratios are mentioned in the question is very important. In this case, order is one rupee, 50 paisa and 25 paisa and ratio is 1:8:16. Thus,
Number of 50-paisa coins = 8x
Number of 25- paisa coins = 16x
Now,Total money in the bag = Rs. 495
- x+ (8x/2) + (16x/4) = 495
(50 paisa coins divided by 2 to convert into rupee and 25 paisa coins divided by 4 to convert into rupee)
- 9x = 495
- x = 495/9
- x= 55
Thus, number of 50 paisa coins = 55*8 = 440
|
201 videos|842 docs|2245 tests
|
FAQs on Important Formulas: Ratio and Proportion - General Test Preparation for CUET UG - CUET Commerce
| 1. What are the different types of ratios? |  |
| 2. How can I solve ratio and proportion questions easily? |  |
| 3. What is the difference between ratio and proportion? |  |
| 4. What are some important formulae related to ratio and proportion? |  |
| 5. Can you provide some tricks to remember ratios and proportions? |  |