NCERT Solutions for Class 8 Maths - Playing with Numbers (Exercise 3.4 and 3.5)
Exercise 3.4
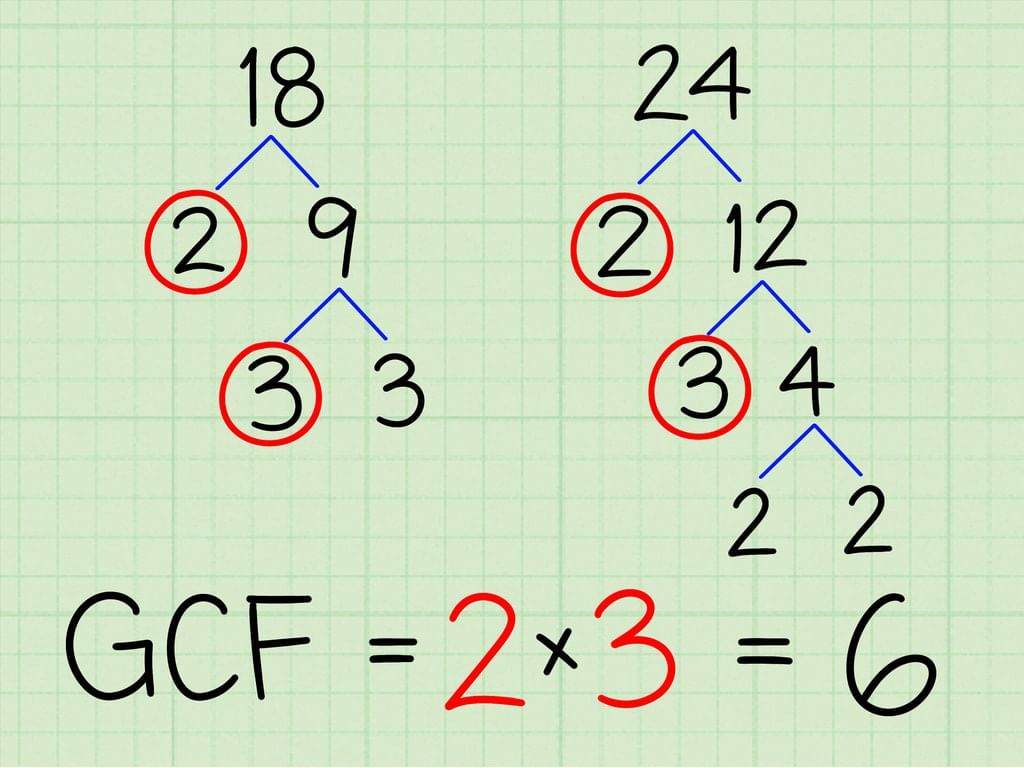 Example for finding common factors
Example for finding common factors
Q1. Find the common factors of:
(a) 20 and 28
(b) 15 and 25
(c) 35 and 50
(d) 56 and 120
Ans: (a) Factors of 20 = 1, 2, 4, 5, 10, 20
Factors of 28 = 1, 2, 4, 7, 14, 28
Common factors = 1, 2, 4
(b) Factors of 15 = 1, 3, 5, 15
Factors of 25 = 1, 5, 25
Common factors = 1, 5
(c) Factors of 35 = 1, 5, 7, 35
Factors of 50 = 1, 2, 5, 10, 25, 50
Common factors = 1, 5
(d) Factors of 56 = 1, 2, 4, 7, 8, 14, 28, 56
Factors of 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 60, 120
Common factors = 1, 2, 4, 8
Q2. Find the common factors of:
(a) 4, 8 and 12
(b) 5, 15 and 25
Ans: (a) Factors of 4 = 1, 2, 4
Factors of 8 = 1, 2, 4, 8
Factors of 12 = 1, 2, 3, 4, 6, 12
Common factors of 4, 8 and 12 = 1, 2, 4
(b) Factors of 5 = 1, 5
Factors of 15 = 1, 3, 5, 15
Factors of 25 = 1, 5, 25
Common factors of 5, 15 and 25 = 1, 5
Q3. Find the first three common multiples of:
(a) 6 and 8
(b) 12 and 18
Ans: (a) Multiple of 6 = 6, 12, 18, 24, 30, 36, 42, 28, 54, 60, 72, …………
Multiple of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, …………………….
Common multiples of 6 and 8 = 24, 48, 72
(b) Multiple of 12 = 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ………
Multiple of 18 = 18, 36, 54, 72, 90, 108, ………………………………
Common multiples of 12 and 18 = 36, 72, 108
Q4. Write all the numbers less than 100 which are common multiples of 3 and 4.
Ans: Multiple of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99
Multiple of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100
Common multiples of 3 and 4 = 12, 24, 36, 48, 60, 72, 84, 96
Q5. Which of the following numbers are co-prime:
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
(d) 17 and 68
(e) 216 and 215
(f) 81 and 16
Ans: (a) Factors of 18 = 1, 2, 3, 6, 9, 18
Factors of 35 = 1, 5, 7, 35
Common factor = 1
Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.
(b) Factors of 15 = 1, 3, 5, 15
Factors of 37 = 1, 37
Common factor = 1
Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.
(c) Factors of 30 = 1, 2, 3, 5, 6, 15, 30
Factors of 415 = 1, 5, …….., 83, 415
Common factor = 1, 5
Since, both have more than one common factor, therefore, they are not co-prime numbers.
(d) Factors of 17 = 1, 17
Factors of 68 = 1, 2, 4, 17, 34, 86
Common factor = 1, 17
Since, both have more than one common factor, therefore, they are not co-prime numbers.
(e) Factors of 216 = 1, 2, 3, 4, 6, 8, 36, 72, 108, 216
Factors of 215 = 1, 5, 43, 215
Common factor = 1
Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.
(f) Factors of 81 = 1, 3, 9, 27, 81
Factors of 16 = 1, 2, 4, 8, 16
Common factor = 1
Since, both have only one common factor, i.e., 1, therefore, they are co-prime numbers.
Q6. A number is divisible by both 5 and 12. By which other number will that number be always divisible?
Ans: Factor of 5 = 1,5
Factor of 12 = 1, 2, 3, 4, 6, 12
Common factor = 1
And the product of these two number is 60.
Factor of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Q7. A number is divisible by 12. By what other numbers will that number be divisible?
Ans: Since the number is divisible by 12. Hence, it also divisible by its factors i.e., 1, 2, 3, 4, 6, 12
Therefore 1, 2, 3, 4, and 6 are the numbers other than 12 by which this number is also divisible
Exercise 3.5
Q1. Here are two different factor trees for 60. Write the missing numbers.
(a)
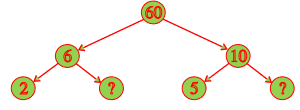
(b) 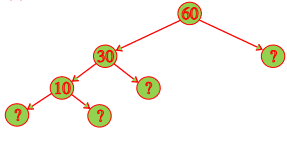
Ans:
(a) Since 6 = 2 × 3 and 10 = 5 × 2
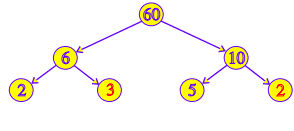
(b) Since 60 = 30 × 2
30 = 10 × 3
10 = 5 × 2
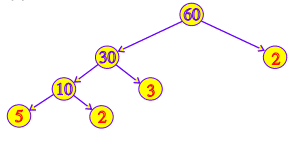
Q2. Which factors are not included in the prime factorization of a composite number?
Ans: 1 is the factor which is not included in the prime factorization of a composite number.
Q3. Write the greatest 4-digit number and express it in terms of its prime factors.
Ans: The greatest 4-digit number = 9999The prime factors of 9999 are 3 × 3 × 11 × 101.
Q4. Write the smallest 5-digit number and express it in terms of its prime factors.
Ans: The smallest five digit number is 10000.
The prime factors of 10000 are 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5.
Q5. Find all the prime factors of 1729 and arrange them in ascending order. Now state the relation, if any, between, two consecutive prime numbers.
Ans: Prime factors of 1729 are 7 × 13 × 19.
The difference of two consecutive prime factors is 6.
Q6. The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Ans: Among the three consecutive numbers, there must be one even number and one multiple of 3. Thus, the product must be multiple of 6.
Example: (i) 2 x 3 x 4 = 24
(ii) 4 x 5 x 6 = 120
Q7. The sum of two consecutive odd numbers is always divisible by 4. Verify this statement with the help of some examples.
Ans: 3 + 5 = 8 and 8 is divisible by 4.
5 + 7 = 12 and 12 is divisible by 4.
7 + 9 = 16 and 16 is divisible by 4.
9 + 11 = 20 and 20 is divisible by 4.
Q8. In which of the following expressions, prime factorization has been done:
(a) 24 = 2 x 3 x 4
(b) 56 = 7 x 2 x 2 x 2
(c) 70 = 2 x 5 x 7
(d) 54 = 2 x 3 x 9
Ans: (a) 24 = 2 × 3 × 4
Since 4 is composite. Hence, prime factorisation has not been done
(b) 56 = 7 × 2 × 2 × 2
Since all the factors are prime. Hence, prime factorisation has been done
(c) 70 = 2 × 5 × 7
Since all the factors are prime. Hence, prime factorisation has been done
(d) 54 = 2 × 3 × 9
Since 9 is composite. Hence prime factorisation has not been done
Q9. 18 is divisible by both 2 and 3. It is also divisible by 2 × 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.
Ans: No. Number 12 is divisible by both 6 and 4 but 12 is not divisible by 24.
Q10. I am the smallest number, having four different prime factors. Can you find me?
Ans: The smallest four prime numbers are 2, 3, 5 and 7.
Hence, the required number is 2 x 3 x 5 x 7 = 210
|
38 videos|22 docs|10 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Playing with Numbers (Exercise 3.4 and 3.5)
| 1. What are the important topics covered in Exercise 3.4 and 3.5 of NCERT Solutions for Playing with Numbers? |  |
| 2. How can one check if a number is divisible by 6? |  |
| 3. What is the rule for checking if a number is a multiple of 9? |  |
| 4. How can one find the sum of digits of a given number? |  |
| 5. Can a number be divisible by both 3 and 9 at the same time? |  |

















